基于OpenGL的遠海島礁海浪模擬

王玉秀，黎 英

（昆明理工大學 信息工程與自動化學院，云南 昆明 650504）

0 引 言

隨著各國學者對海洋領域的不斷探索研究，海浪模擬依托于海浪譜的海浪模擬技術發展迅速，在流體力學、波浪學、計算機圖像學、虛擬現實及軍事行動等諸多領域都發揮了重要的作用。目前，近島礁海浪研究方法主要有三種，即物理模型、現場海洋觀測及數值模型。2002年，李孟國[1]根據線性波動的疊加原理和波浪方向譜理論，推導出了非緩坡非均勻流場中考慮非線性彌散影響和底摩擦作用的多向不規則波傳播的折射繞射方程。2013年，STEPHEN G[2]通過實測Moorea北岸的陡峭珊瑚前礁和潟湖內的波浪、增水、波生流，發現研究測量結果與線性波理論吻合良好。2020年，王紅川[3]等利用近岸波浪傳播變形的拋物型緩坡方程和波能流平衡方程，推導出了適用于斜坡上波浪破碎的數值模擬方法，該模型可以較好地模擬斜坡地形的波浪傳播波高變化情況。盡管近幾年國內外學者[4-9]對海浪數值模擬進行了大量的研究，但是由于遠海島礁的特殊性以及海浪的高度隨機性，很難用一種精確的模型對其進行描述。近年來，計算機仿真技術被廣泛應用于近海海浪的仿真模擬，OpenGL因其開放性和高效性被應用于多種仿真建模場景中，能呈現出較好的模擬效果[10-14]。在模擬時往往直接采用近岸模擬的方法進行近似模擬，忽視了遠海島礁自身的特殊性。遠海島礁距離海岸較遠，地形構造特殊，較開闊海域具有更加復雜的變化情況。本文將就數值模型展開對遠海島礁海浪的研究，針對經典P-M海浪譜無法適應復雜海浪情況的問題，對其添加島礁因子進行海浪修正，并利用Gerstner波進行環島礁海浪模擬，兼顧了遠海與島礁兩者的特性。

1 海浪模型介紹

1.1 P-M海浪譜

P-M模型的頻率分布公式為：

海浪的生成因素較為復雜，其傳播方向同時受到多種力的共同影響，并非與風的方向完全一致，因此模擬過程要充分考慮海浪生成的多種影響因素。對于波浪傳播方向的角度分布而言，可以利用Mitsuyasu公式進行計算，從原來的一維譜函數變成二維譜函數，完成對波幅的計算。

Mitsuyasu公式給出了頻率f、相對于風的角度θ的波的能量：

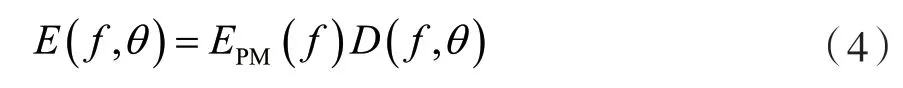
波幅的計算依賴于色散關系和傅里葉變換。色散關系通常指波傳播過程的頻率依賴現象，色散關系公式為：

經過傅里葉逆變換即得計算波幅的公式為：

海浪的形態并不是規則的，常用的參數曲線無法完成這一表示過程。故利用（x，y，z）坐標值來進行圖像繪制。對x值和y值進行預設，將z值作為波幅值和能量分散方向的正弦值之積，對海浪高度進行求解。

1.2 Gerstner波

基于Gerstner波的海浪建模最早由FOURNIER和REEVES[15]引入計算機圖形學，其計算量不大。Gerstner波屬于有限振幅波理論，滿足Lagrange方程[16]，模擬波形較真實，被廣泛應用于水波模擬，其基礎參數方程如下：

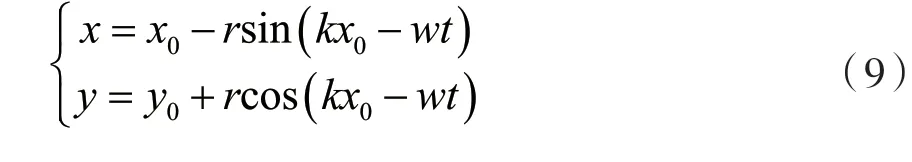
式中：r為波幅，k為波數，w為角頻率。該方程考慮時刻t時波浪經過的情況。

2 海浪算法改進及海面設計

2.1 島礁因子

經典的Pierson-Moskowitz模型代表了充分生長的海浪譜，這一點與本次研究的遠海波浪部分非常契合，因此在遠海部分選用P-M海浪譜來對海面進行模擬，但當波浪從遠海傳播至島礁附近，經過礁坪前地形劇烈變化地帶時波高增大后迅速減小[17]。P-M海浪譜僅與海面上方的風速有關，當海浪受到較大的外力時便不再適用，使得該海浪譜在復雜環境的情況下就會失去其優勢。為了彌補這一缺陷，結合本次研究的遠海島礁環境，提出島礁因子這一控制要素，對近島礁海浪的無序變化進行簡化表述。島礁因子的算法流程如圖1所示。

圖1 島礁因子算法流程圖

島礁因子通過控制海浪的波幅進而控制海浪的形狀，實現相應的模擬效果。對于遠海海域，島礁因子不會對其產生影響，只有在達到近島礁這一觸發條件時，島礁因子才會發揮其作用。根據圖1的算法流程，在此給出島礁因子的公式形式：

式中：位置參數Lt為該點的(x,y)的坐標值平方和，比例因子q為位置參數length和島礁半徑平方的比值，lers為島礁半徑平方。

得到島礁因子la之后，結合已經得到的海浪幅值公式給出添加島礁因子之后的幅值公式：

為了驗證島礁因子是否可以有效地對近島礁海浪模擬進行優化，進行模擬仿真實驗。為了實現動態起伏的海面，采用網格繪制的方法，通過對每一個點的高度值進行計算，得到高低起伏變化的海面。網格上的每個點的高度隨著時間的變化而變化。為了對遠海島礁進行較為完整的顯示，設置整個模擬海面的規格為256×256個海浪網格單元。首先利用坐標函數對各坐標點進行設置，此時每個坐標點都將獲得由（x，y，z）3個參數構成的坐標值，同時對海面的起始高度、島礁高度以及島礁的半徑等設置參數進行表示。其次，獲得模擬時該點的島礁高度，設定海岸的高度預設值。當島礁坐標小于預設值，則表示未達到海岸線，模擬繼續按照遠海海浪譜進行；如果島礁的高度大于預設值則表示海浪到達海岸處，在此處發生海浪高度的改變。獲得需要處理的島礁坐標之后，求解此點距離島礁中心的距離，海浪在拍擊海岸之后能量逐漸消散，根據距離的不同海浪高度也不盡相同。加入了島礁因子后，采用遍歷的算法對整個島礁海浪進行計算，對坐標點進行篩選后進行相應的數值計算。遍歷算法本身較為簡潔，在部分情況下時間復雜度較高，但在本次模擬仿真中實現了較好的模擬效果，保證了實時性。

通過模擬仿真實驗進行細節對比。圖2給出的是原P-M海浪譜在島礁地形下的海面情況，圖3給出的是加入島礁因子改進后的海面模擬效果。可以明顯地看出，改進之后的海浪形狀更接近實際情況，說明島礁因子的加入彌補了原PM海浪譜無法模擬復雜海況的缺陷。

圖2 原P-M海浪譜模擬的海浪

圖3 基于改進后P-M海浪譜模擬的海浪

2.2 海面設計

2.2.1 環島海浪

海浪在由遠及近的傳播過程中會遇到島礁等障礙物，水深落差致使海浪發生折射、繞射、反射以及海浪破碎等現象，特別是由于背浪側繞射現象的存在，使得背浪側會產生相應的近岸浪。環島海浪的形成原理如圖4所示。

圖4 環島浪形成原理

在對環島海浪進行模擬時，僅采用Gerstner波的豎直方向分量進行模擬。由于環島海浪只會出現在近島礁區域，所以此處根據島礁因子為環島浪設定觸發條件。當島礁因子為1時，表示選取的坐標點不屬于研究范圍內的島礁地形，此時的環島波浪振幅趨于0，按照遠海海浪進行模擬，使環島海浪失效，以此控制環島海浪的模擬范圍，同時得到環島海浪最終的參數方程如下：

疊加環島海浪后的海浪細節如圖5所示。可以看出，添加環島浪后，模擬出的海浪更接近于實際近島礁海浪情況。

圖5 添加環島海浪后的島礁海浪

2.2.2 整體海面構建

依據波的疊加原理，可以將復雜的波分解為一系列的簡諧波組合。依據這一原理，將改進后的P-M海浪譜同設計的環島海浪進行波的線性疊加，最終得到整個海面的海浪模型。之后利用OpenGL和Microsoft Visual Studio（VS）進行仿真模擬實驗，海面場景的實現大致分為以下幾個步驟。

步驟1：設置開發環境。在VS上創建控制臺程序，然后鏈接OpenGL庫文件。

步驟2：建立程序框架。首先需要建立OpenGL和Windows窗口兩者之間的連接；其次設置所需的像素格式，以求達到最佳的效果；最后設置窗口的圖形變換以及窗口函數的銷毀。

步驟3：海面網格的繪制。為了實現動態起伏的海面，采用網格繪制的方法，利用OpenGL中的繪圖函數繪制網格的頂點、直線以及網格多邊形。然后依據改進后的算法函數模型對每一個點的高度值進行計算，網格上的每個點的高度隨著時間變化而變化，從而得到高低起伏變化的動態海面。

步驟4：光照與渲染。通過設置環境光、反射光以及鏡面指數等對海面和島礁的材質進行設置，啟用光源之后，整個場景呈現出較好的質感。同時利用glTexImage2D函數和glTexCoord2f函數進行渲染，紋理源來自真實照片，然后對各個網格進行映射，此種紋理映射方法可以使仿真結果具有較好的真實感，并且可以提高整個系統的運算速率。a、b兩個不同時刻的海浪效果如圖6、圖7所示。

圖6 a時刻遠海島礁海浪網格圖

圖7 b時刻遠海島礁海浪網格圖

3 仿真實驗與結果分析

本次實驗以遠海島礁海浪為研究對象，實驗的硬件平臺為AMD Ryzen 5 3600X 6-Core Processor 3.80 GHz CPU、NVIDIA GeForce RTX 2060顯卡，開發環境為Visual Studio 2017和OpenGL，運行環境為64位Windows 10系統。利用計算機技術對波浪進行模擬，為了繪制出仿真精度、逼真度較好的遠海效果，波面網格選用256×256的規格。用C++語言進行程序編寫，C++語言靈活、功能強大，運行效率是其最大的優勢。經過測試，幀率穩定地保持在15 f·s-1以上，能夠較好地實現所需的仿真效果。渲染之后的海浪效果如圖8所示，可以看出，模擬實驗的結果很好地兼顧了遠海海浪以及環島礁海浪的特性，實現了完整的遠海島礁海浪模擬。

圖8 遠海島礁海浪模擬圖

4 結 語

本文針對P-M海浪譜模型無法模擬近島礁海浪的局限性，通過構建島礁因子來對其進行改進。之后分析了環島海浪的成因，并以Gerstner波為原型對其進行設計，同時將島礁因子設為環島海浪的觸發因子。最后依據波的線性疊加原理完成整個遠海島礁海浪場景的設計，利用OpenGL和VS完成了海面的3D模擬效果，整個海面具有較強的真實性。由于海浪的高度隨機性，本文未考慮海浪與島礁的碰撞檢測問題，在后續的研究工作中，將就這一問題展開著重研究。