基于ABAQUS二次開發對某機載吊艙的損傷容限分析
楊一帆 邰煒華 張敏強 李 智 蘇力爭
(西安電子工程研究所 西安 710100)
0 引言
損傷容限設計理論是一種以斷裂力學為基礎的設計理論,常用于飛機的整機設計與機載設備設計。由于機載設備在使用過程中,會受到因飛機的各種機動動作而產生的重復載荷作用,使得機載設備的某些關鍵承力部位承載能力下降,易產生疲勞損傷與疲勞斷裂[1-4]。目前結構的損傷容限分析方法主要有實驗法、工程公式法與有限元法。由于有限元法具有高效性與易編程性等特點,使得有限元法在解決結構損傷容限問題上得到了廣泛應用[5-8]。
1 損傷容限基本理論
損傷容限理論是為了確立結構剩余強度,裂紋擴展速率與設備檢修周期三者關系而存在一種結構設計理論。由于結構件在加工,運輸,使用過程中會產生不易發現的缺陷與損傷,這些缺陷與損傷會隨著載荷的作用而逐漸加重,致使結構件產生破壞,影響其使用的安全性與可靠性。結合斷裂力學[9]理論知識,可以有效地解決大多工程實際問題,為結構設計的安全性提供了一種可以定量評估的方法。
損傷容限設計的主要目的是通過恰當的材料選擇與合理的結構布局來保證結構件在檢修周期內不會發生斷裂與破壞,使設備的使用可靠性得到提升。由于機載設備的特殊工作環境,使得損傷容限設計理論在機載設備的結構設計中具有重要意義。
2 基于Python語言對ABAQUS的二次開發
2.1 二次開發程序基本結構
運用Python語言對ABAQUS軟件進行二次開發,使ABAQUS軟件可以對模型的損傷容限進行自動分析,輸出各裂紋長度下的應力強度因子幅度ΔK。基于Python語言對ABAQUS軟件二次開發的程序流程圖如圖1所示。
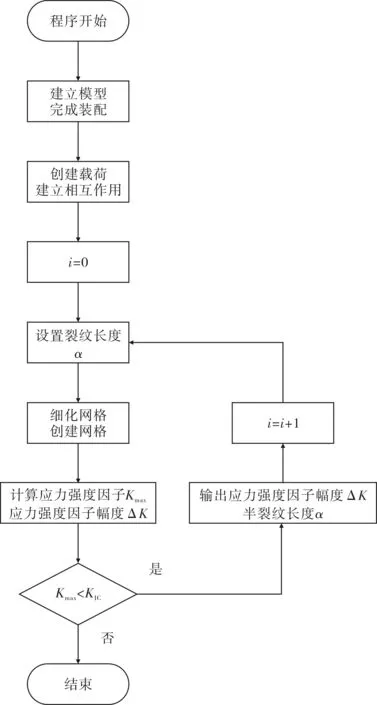
圖1 ABAQUS二次開發程序分析流程
ABAQUS軟件的二次開發程序可以自動完成對結構件的建模,裝配,施加載荷,建立相互作用,創建網格等有限元計算的前處理。通過一個循環語句對裂紋進行自動設置,提高了有限元計算的效率,減少了人為重復修改裂紋數據的時間。
2.2 不同算例的損傷容限分析
2.2.1 斷裂條件與材料選擇
如圖2所示,裂紋的主要形式有三種,本文主要對I形裂紋進行分析與計算。如圖3所示,疲勞裂紋擴展主要分為三個階段,裂紋初始萌生階段,裂紋穩定擴展階段,裂紋快速擴展階段,損傷容限理論所研究的是裂紋的穩定擴展階段。
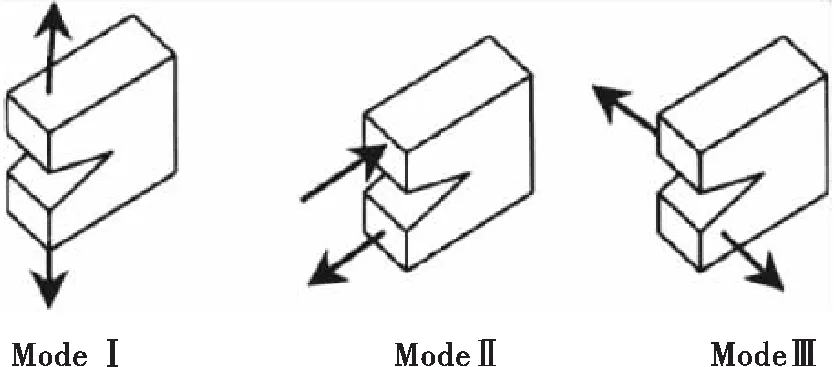
圖2 裂紋類型
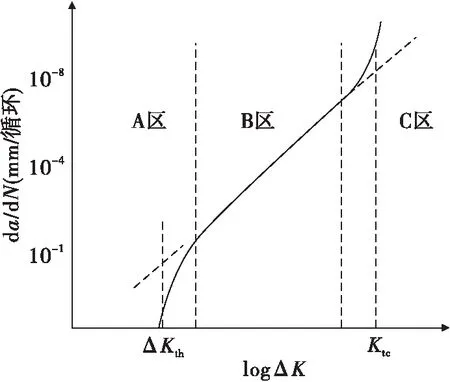
圖3 疲勞裂紋擴展階段
為了使疲勞裂紋開始擴展,應力強度因子幅度ΔK應滿足
ΔK>ΔKth
(1)
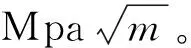
疲勞裂紋瞬間斷裂,應力強度因子最大值KImax應滿足
KImax≥KIc
(2)
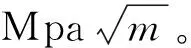
算例的材料選取2A12鋁合金,材料參數如表1所示。

表1 材料參數
2.2.2 算例的結構尺寸
運用三維繪圖軟件UG對三種不同尺寸的算例進行建模,具體尺寸如圖4所示。
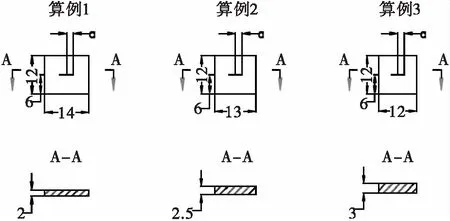
圖4 不同算例結構尺寸
圖4中a為初始預制半裂紋長度,單位為mm。
2.2.3 基于程序對不同算例的損傷容限分析
通過運行程序,實現對算例的自動分析,在計算中,取循環載荷應力比R為0.06,最大載荷σmax為3500N/Wt,式中t為算例厚度,單位為mm;W為算例寬度,單位為mm。初始半裂紋長度α為2mm。
(3)
式(3)中σmin為循環載荷的最小載荷單位為Mpa,σmax為循環載荷的最大載荷,單位為Mpa。
部分計算云圖如圖5至圖7所示。
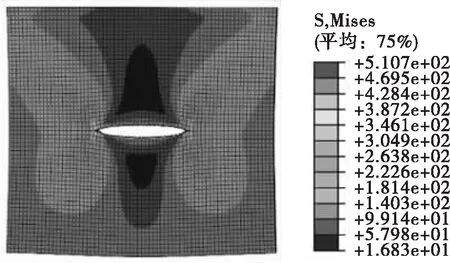
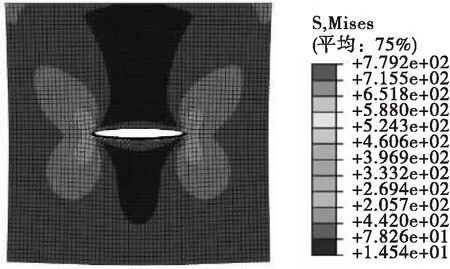
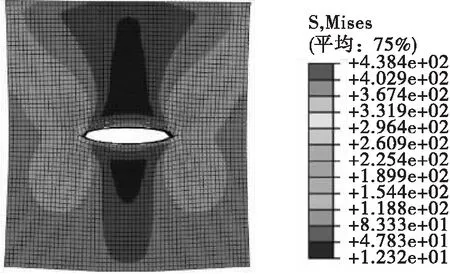
如應力云圖所示,裂紋尖端形成塑性區,且隨著裂紋的擴展,裂紋尖端的應力集中現象逐漸增強。通過程序計算得到應力強度因子幅度ΔKI隨半裂紋長度α的變化曲線如下所示:
如圖8所示,隨著裂紋的擴展,應力強度因子幅度ΔKI逐漸增大,并最終達到斷裂條件,致使算例瞬間斷裂破壞。
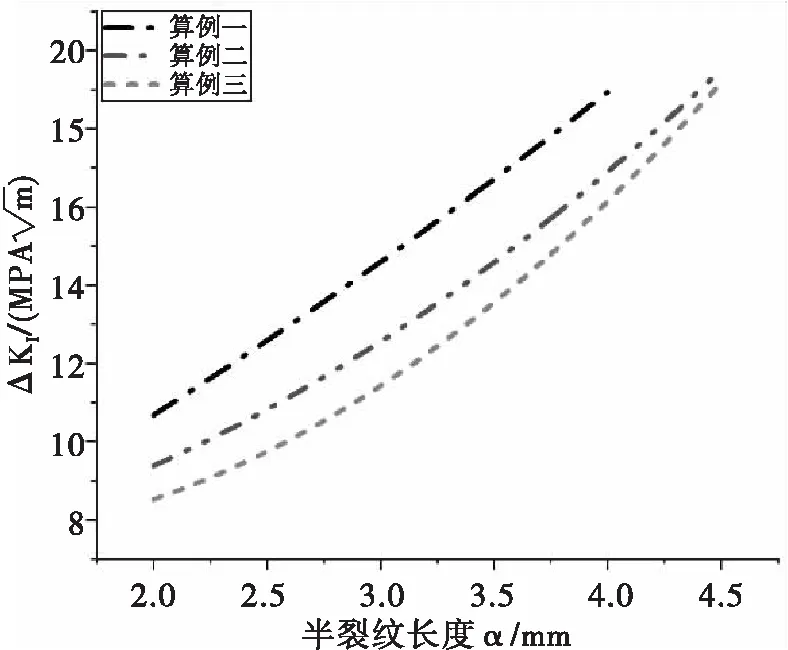
圖8 ΔKI變化趨勢圖(程序計算)
Paris公式為
(4)
式(4)中C,n為材料常數,Paris公式是用于描述恒幅載荷作用下的疲勞裂紋擴展速率。將Paris公式積分可以得到式(5)。
(5)
式(5)中△σ為載荷幅度,單位為Mpa,△α為裂紋擴展長度,單位為m;α0為初始裂紋長度,單位為m;J為裂紋穿透因子。通過式(5)可以得到三種算例基于程序計算結果的疲勞裂紋擴展壽命曲線。
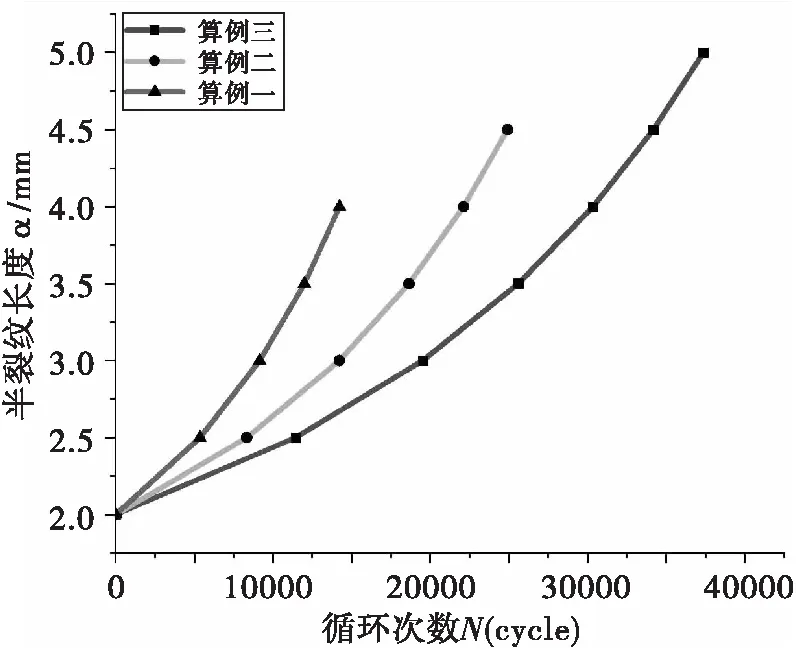
圖9 不同算例α-N曲線圖(程序計算)
2.2.4 工程算法對不同算例的損傷容限分析
通過查詢損傷容限手冊[10]可以得到中心穿透裂紋板應力強度因子KI的計算公式為
(6)
最大應力強度因子為
(7)
應力強度因子幅度為
(8)
Δσ=σmax-σmin
(9)
其中σ為中心裂紋板所受均布載荷,單位為Mpa;J1為裂紋穿透因子;α為中心半裂紋長度,單位為mm;σmax為循環載荷最大值,σmin為循環載荷最小值,單位為Mpa;R為循環載荷應力比;Δσ為載荷幅度,單位為Mpa。
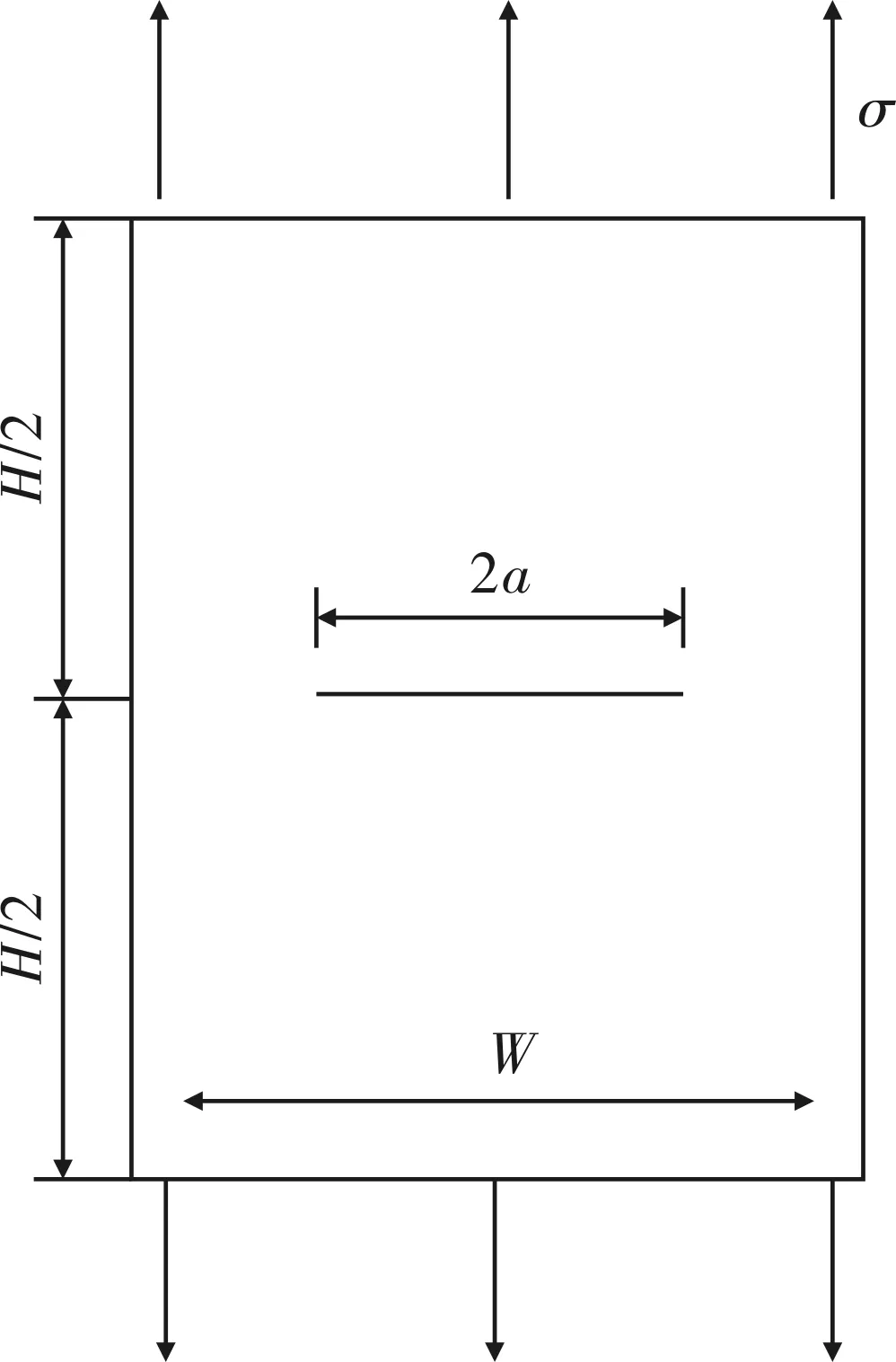
圖10 中心穿透裂紋板示意
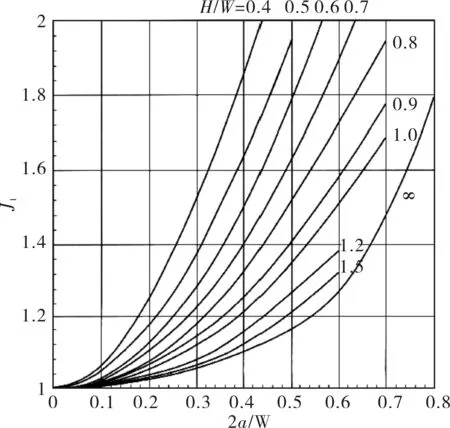
圖11 穿透因子變化曲線
計算條件與程序計算時一致,通過工程算法得到應力強度因子幅度ΔKI隨半裂紋長度α的變化曲線如圖12所示。
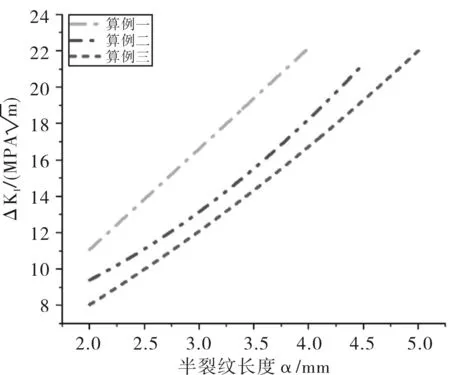
圖12 ΔKI變化趨勢圖(工程計算)
同樣通過式(5)可以得到三種算例基于工程計算結果的疲勞裂紋擴展壽命曲線如圖13所示。
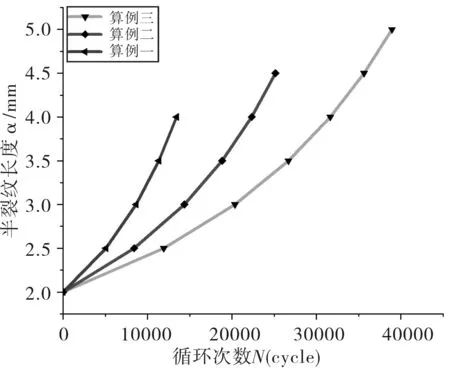
圖13 不同算例α-N曲線圖(工程計算)
2.2.5 數據對比與分析
為了驗證ABAQUS二次開發程序的準確性與可靠性,本節將對三個不同尺寸算例的損傷容限分析數據進行對比。
首先對兩種方式計算得到的應力強度因子幅度ΔKI進行對比。如圖(14)所示,算例一ΔKI的平均相對誤差為10.68%;算例二ΔKI的平均相對誤差為5.03%;算例三ΔKI的平均相對誤差為3.28%,相對誤差均小于15%,滿足工程需求。

(a)算例一
對兩種方式計算得到的疲勞裂紋擴展壽命曲線α-N曲線進行對比;如圖15所示,所有α-N曲線的趨勢基本相同,隨著裂紋的擴展,裂紋擴展速率逐漸增大。算例一α-N曲線的平均相對誤差為6.03%;算例二α-N曲線的平均相對誤差為1.12%;算例三α-N曲線的平均相對誤差為4.03%,相對誤差均小于15%,滿足工程需求。本節旨在驗證ABAQUS軟件二次開發程序,為后續分析計算打下基礎。
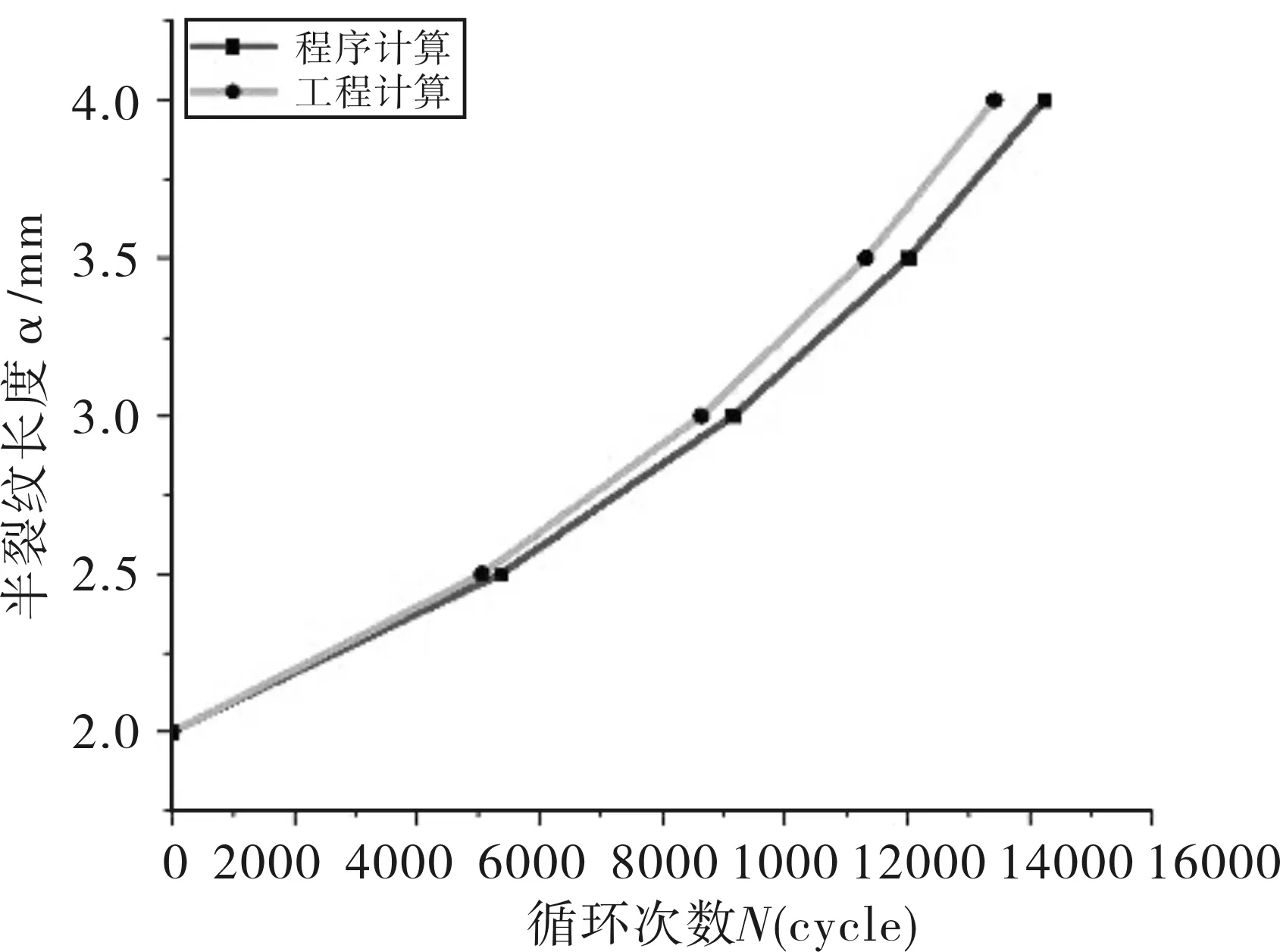
(a)算例一
3 某機載吊艙的損傷容限分析
3.1 某機載吊艙的結構與試驗條件
如圖16所示,某機載吊艙通過兩個吊耳與總站連接,主要承力部位為吊耳部位,吊耳材料為2A12鋁合金。按照研制要求,該機載吊艙需能夠承載峰值為20g的重復沖擊載荷(三軸六向),沖擊波型為后峰鋸齒波,單次沖擊持續時間為11ms,吊艙總重為50kg。通過對吊耳結構的分析計算可以得到:吊耳對垂直向下方向的沖擊最為敏感,即垂直向下的沖擊對吊耳的威脅最大。
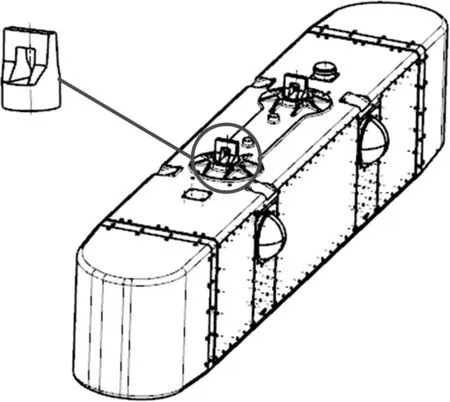
圖16 機載吊艙結構示意
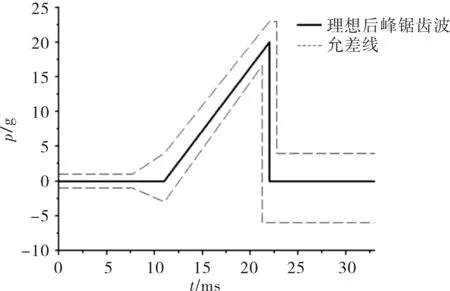
圖17 沖擊載荷波形圖
運用有限元軟件ABAQUS對吊艙進行靜力分析,得到吊耳的危險位置如圖18所示。
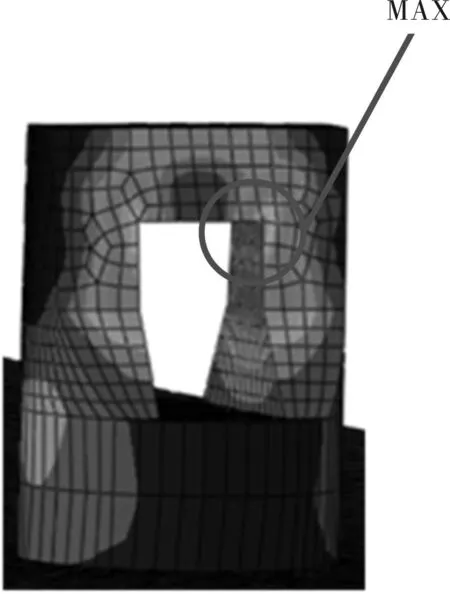
圖18 危險位置示意
3.2 計算結果分析與壽命預測
為了簡化計算,提高運算效率,將吊耳模型進行簡化處理。機載設備的疲勞破壞,是多種因素共同作用造成的,如結構加工缺陷,腐蝕,結構過載,維護不當等,固對吊耳兩側的危險部位預制裂紋,預制半裂紋長度為α,單位為mm,如圖19所示。
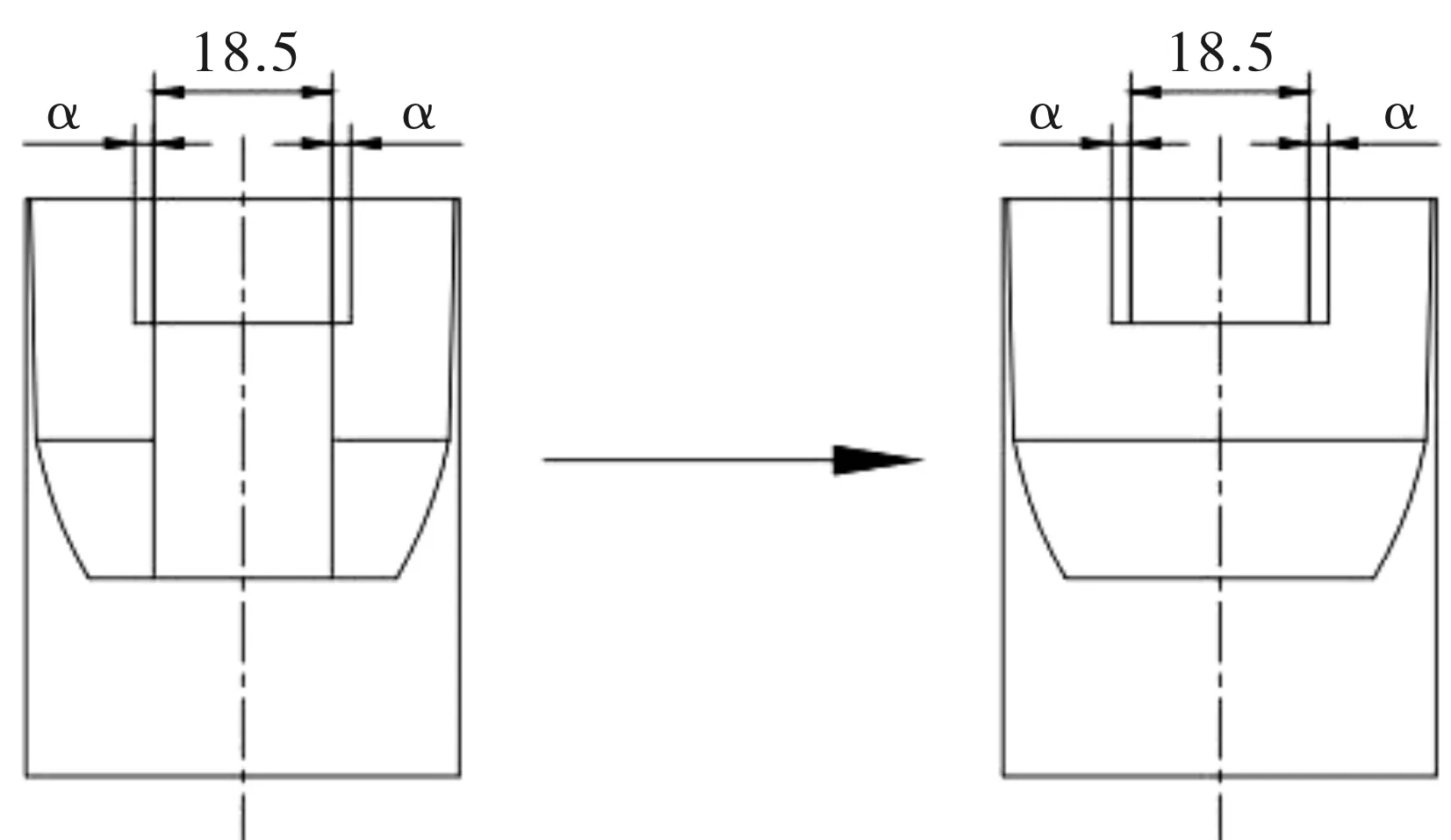
圖19 吊耳簡化模型
通過編寫程序,使吊耳在自動建模時,網格選擇C3D8R減縮積分六面體網格,并對吊耳結構進行拆分,以提高網格質量,提升計算準確性,應力比R取0.06。結構拆分及網格劃分如圖20所示。
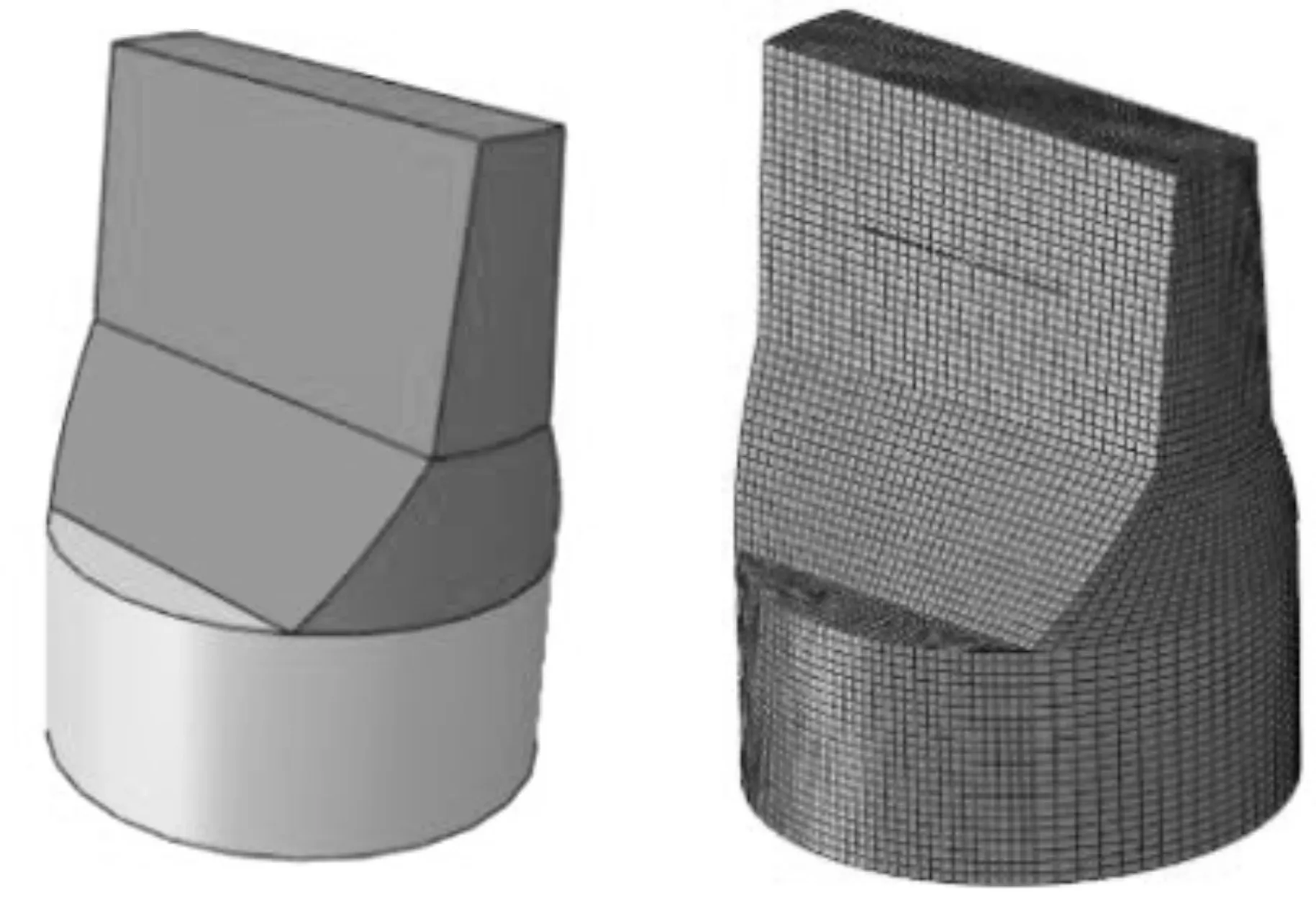
圖20 拆分及網格劃分
通過程序計算得到的應力強度因子幅度△K與半裂紋長度α的關系如圖21所示。
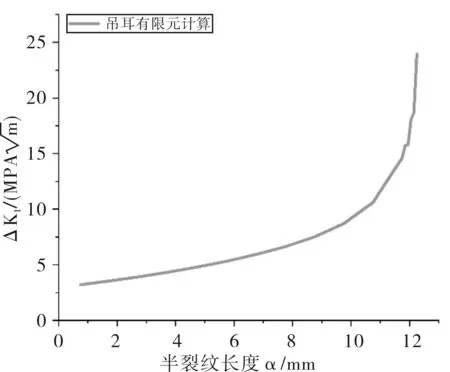
圖21 吊耳ΔKI變化趨勢圖
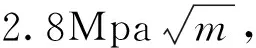
部分裂紋長度下的應力云圖如圖22所示:
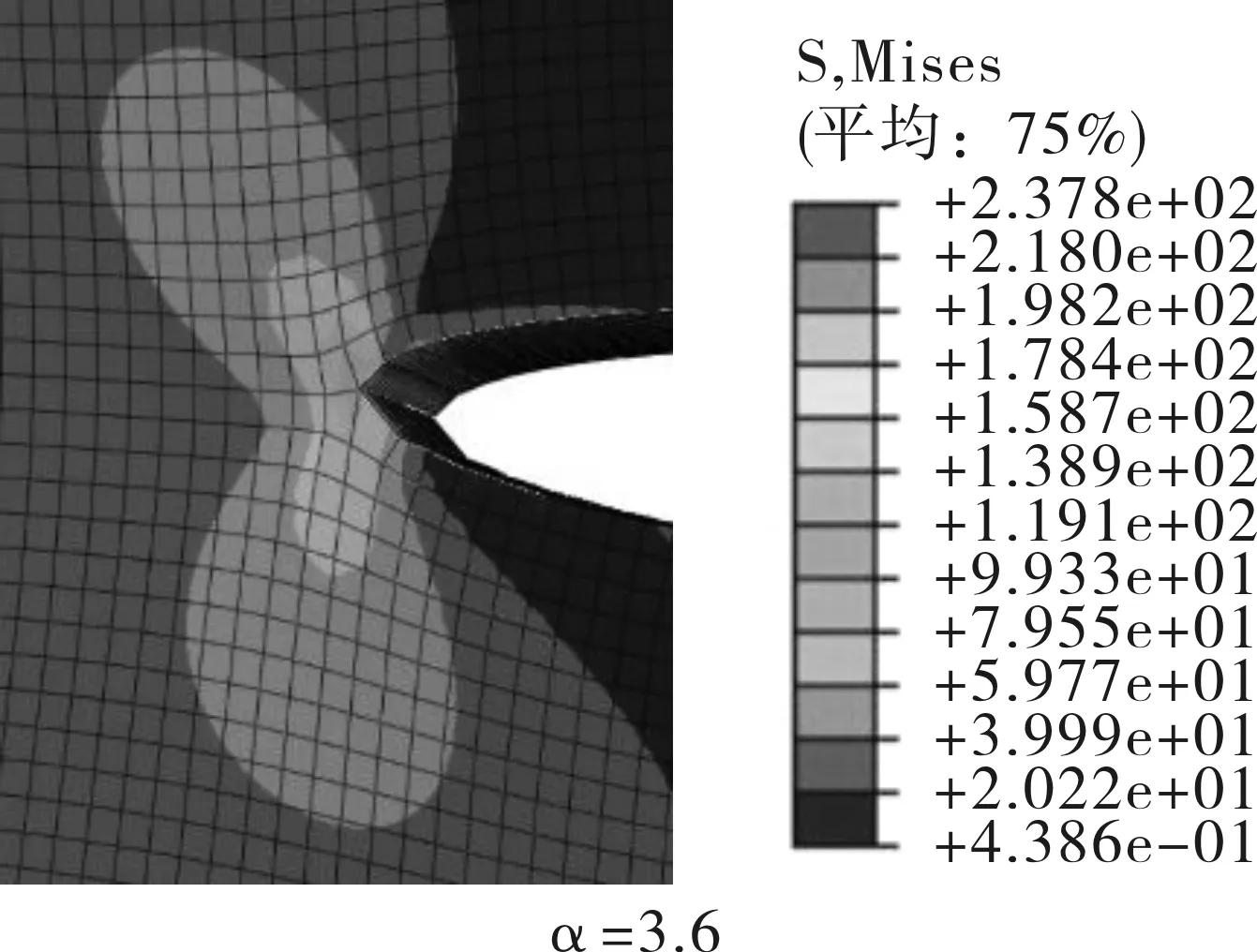
將不同裂紋長度αi+1=αi+Δα帶入式(5)可以推算出吊耳在沖擊載荷作用下的疲勞壽命曲線,如圖23所示。
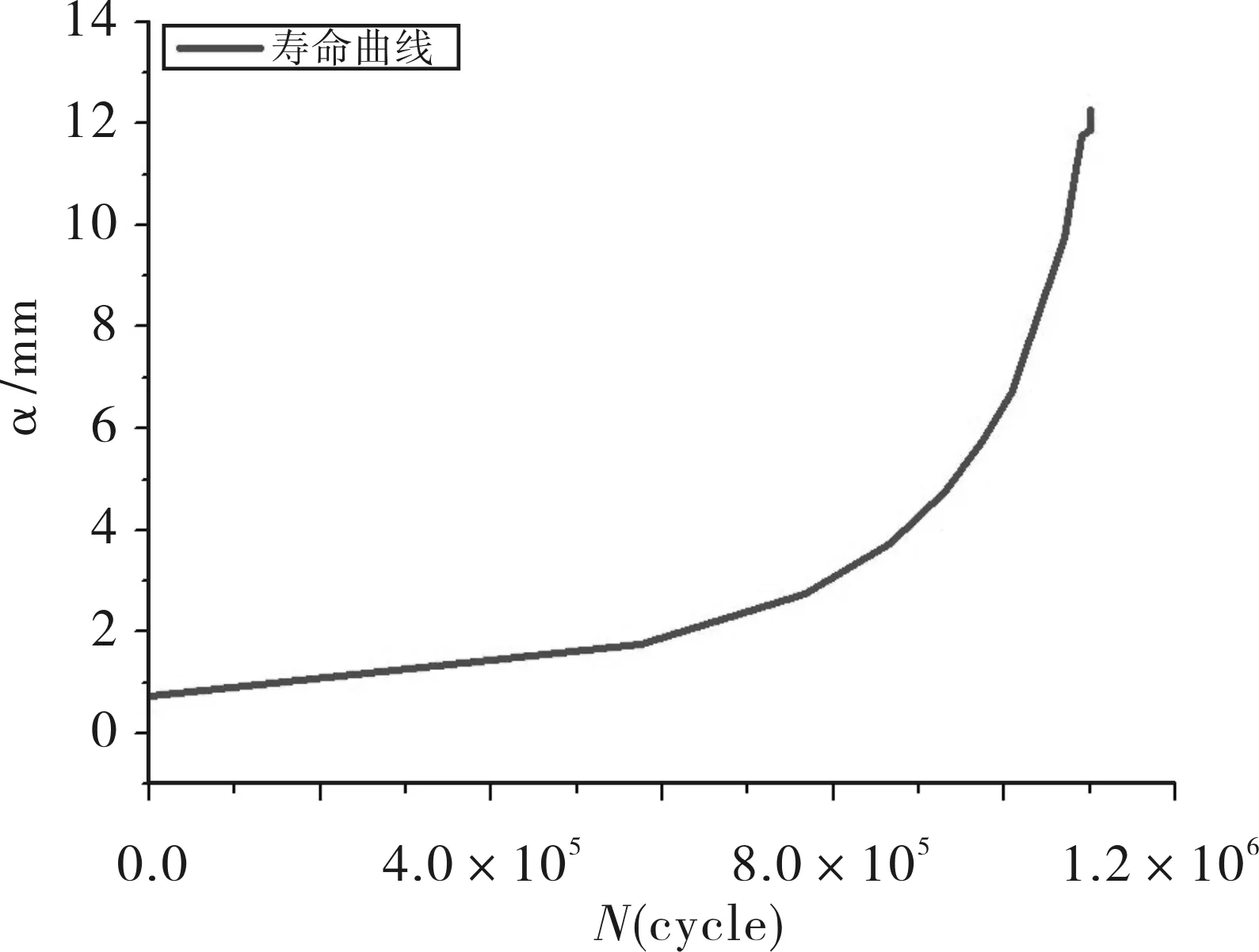
圖23 吊耳疲勞裂紋擴展曲線
從圖23可以看出,隨著疲勞裂紋的增長,疲勞裂紋擴展速率也在增大。機載吊艙吊耳在初始半裂紋長度α=0.7mm的條件下,疲勞裂紋擴展壽命為1.15×106。由此可以得出,結構在該循環沖擊載荷作用下的剩余強度較高,且裂紋開始擴展所需的初始裂紋長度較大,此初始裂紋在設備日常檢修時通過觀察比較容易發現。綜上所述,該結構滿足損傷容限設計要求與實際工程使用需求。
4 結束語
本文應用Python語言對ABAQUS軟件進行二次開發,通過對不同結構算例的損傷容限分析,驗證了二次開發程序計算的準確性與可靠性,各算例通過程序計算的結果與工程經驗公式計算結果的相對誤差均不超過15%,滿足工程需求,并對各算例的疲勞壽命進行了預估。運用二次開發程序,對某機載吊艙危險部位進行損傷容限分析,通過程序輸出數據分析某機載吊艙危險部位的開裂條件,并對結構的疲勞壽命進行了預估,為某機載吊艙關鍵承載部位檢修周期的制定提供了理論依據,并從損傷容限分析的角度驗證了某機載吊艙結構設計的安全性與可靠性。為結構的損傷容限設計提供了一種驗證與計算的方法。

