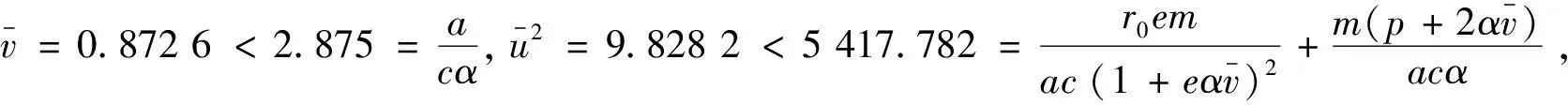具協作狩獵和恐懼效應的擴散捕食者-食餌系統分析
劉宇鑫, 張繼民
(黑龍江大學 數學科學學院, 哈爾濱 150080)
0 引 言
捕食關系是自然系統中最基本的關系之一, 在種群進化、保護生物多樣性方面發揮著重要作用[1-2]。很多捕食者都是群居生活, 在捕食過程中,為了捕獲獵物, 它們之間需要相互協作狩獵, 這樣極大地提高了捕食者的生存率。捕食者不僅可以直接捕殺食餌, 也可以對食餌產生間接影響, 形成一種捕食者恐懼效應, 導致食餌棲息地的變更、覓食習慣的改變和生殖率下降等。
在文獻[3]中, 學者Alves等首先建立了一個具協作狩獵的捕食者-食餌系統, 通過數值模擬研究了系統平衡點的存在性及穩定性、分支的存在性。Pal等討論了一個離散的具協作狩獵的捕食者-食餌系統的動力學性質, 數值模擬顯示協作狩獵可以引起混沌行為[4]。Banerjee等考慮了一個三種群捕食系統, 捕食者協作狩獵兩個互惠的食餌[5]。Song等考慮了具協作狩獵的擴散捕食者-食餌系統, 并證明系統具有圖靈結構[6]。在文獻[7]中, Wang等首先提出了一個兩維具食餌恐懼效應的捕食者-食餌系統, 指出恐懼效應能夠穩定捕食者-食餌系統。在此之后, 許多具有不同背景的具食餌恐懼效應的捕食者-食餌系統被研究和分析[8-10]。
基于上面的分析和討論, 本文主要研究一類具協作狩獵和恐懼效應的擴散捕食者-食餌系統
(1)
式中:u表示食餌種群密度;v表示捕食者種群密度;Ω是n中一個有界區域且具有光滑的邊界;r0是食餌出生率;d是食餌死亡率;a是食餌種內競爭系數;p是捕食者捕食率;α是協作狩獵參數;m是捕食者死亡率;e是恐懼效應參數;c是營養轉化率;d1,d2分別表示食餌種群和捕食者種群的擴散系數。本文中假設所有的模型系數都是正的。
本文主要目的是分析系統(1)的動力學性質。第1節是系統的基礎動力學性質, 包括解的全局存在性和耗散性。第2節探討系統常值穩態解的存在性和局部穩定性, 并給出Hopf分支的存在性。第3節利用數值模擬驗證所得結果。
1 解的全局存在性和耗散性
研究系統(1)解的長時間性質, 包括全局存在性和耗散性。

定理2若(u(x,t),v(x,t))是(1)的任意一個非負解, 則
(2)

證明設(u(x,t),v(x,t))是系統(1)的任意一個非負解, 則
由拋物方程的比較定理可知,式(2)的第一個不等式成立。

因而有

2 常值穩態解和Hopf分支
系統(1)的常值穩態解的存在性和穩定性及Hopf分支存在性。系統(1)的常值穩態解有
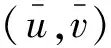
(3)
為了獲得常值穩態解的穩定性, 令
μi∈Λ:={μi:0=μ0<μ1<…<μi<…,i∈0}
(4)
是具齊次Neumann邊界條件算子-Δ在Ω上的特征值, 其中0:=∪{0}。定義
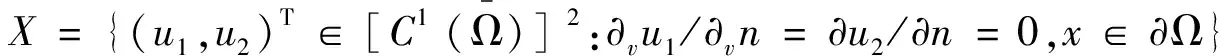

(5)
式中(φ,φ)∈X, 并且
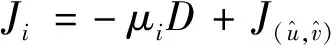
四季柚嫩梢長到20 cm要摘心,一般采用疏剪叢生瘦弱新枝梢或交叉的1-2年生枝梢,不宜重修剪;對樹冠郁蔽、內膛通風透光差的單株,則適量“開天窗”疏大枝(多年生的),改善樹冠內膛通風透光性能。重剪衰老樹和樹勢弱樹,促發新梢或更新樹冠。采用短剪,刺激生長勢較弱的枝梢抽生強壯的新梢。
λ2-Tiλ+Di=0,i∈0
式中
定理3E0總是存在的, 且若d>r0, 則E0是局部漸近穩定的。
證明由式(4)和式(5)可知,系統(1)在E0處對應的線性化系統k階特征方程為
λ2-(-(d1+d2)μk+r0-d-m)λ+(d1d2μk+(d1m-(r0-d))μk-(r0-d)m)=0
若d>r0, 則對任意的k∈0, 特征值實部均為負的, 因而E0是局部漸近穩定的。
定理4(i)若d
證明由E1表達式知(i)成立。根據式(4)和式(5)可知,系統(1)在E1處線性化系統對應的特征方程為
(λ+d2μk+(r0-d))(λ+d1μk+m-cp(r0-d)/a)=0
若m>cp(r0-d)/a, 則對任意的k∈0, 特征值實部均為負的, 因而(ii)成立。
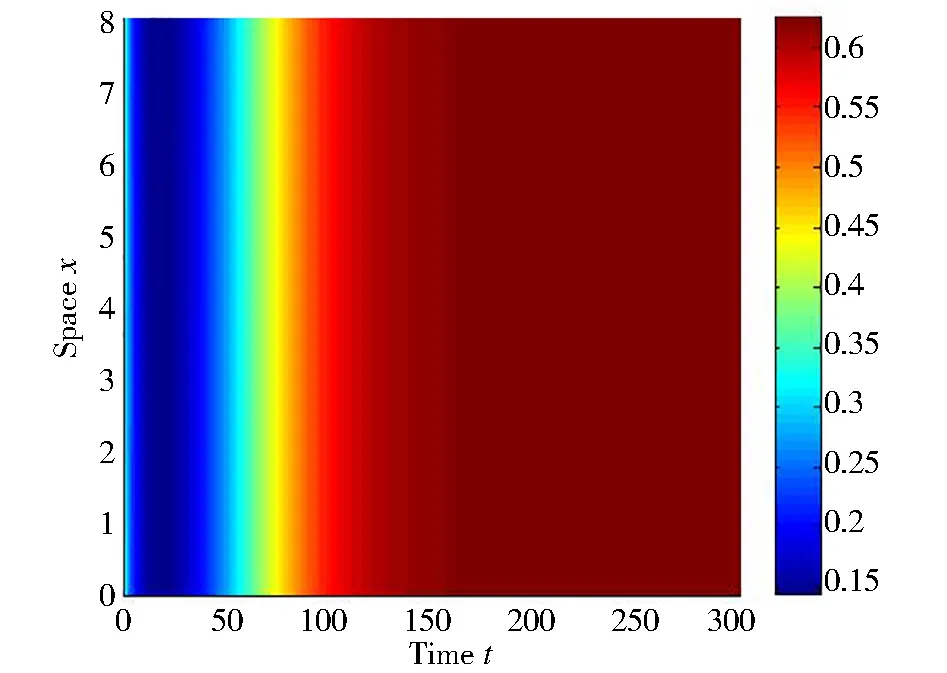
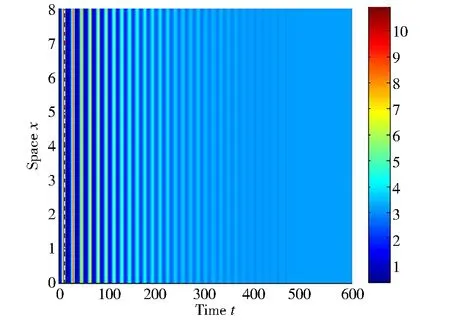
定理5(i)若m (ii)若 (6) 則E2是局部漸近穩定的。 ceα3v4+(cα2+2cepα2)v3+(2cpα+cep2α)v2+A1v+A0=0 (7) 式中 A1=cp2+cdepα+aemα+cα(d-r0),A0=am+cp(d-r0) 根據笛卡爾符號規則, 若A0<0, 則式(7)存在唯一的正根, 于是E2存在且唯一。 由式(4)和式(5)知,系統(1)在E2處線性化系統對應的特征方程為 λ2-Tkλ+Dk=0,k∈0 (8) 式中 (9) 因而, 若式(6)成立, 則E2是局部漸近穩定的。 證明由式(9)可得 因而定理結論成立。 利用Matlab進行數值模擬, 驗證前面所得的相關理論結果。 (1)圖1顯示捕食者和食餌都滅絕。這里r0=0.4,m=0.02,a=0.01,e=1,α=0.01,p=0.1,d=0.401。因為r0=0.4<0.401=d,所以定理3的條件成立,E0是漸近穩定的。 圖1 常值穩態解E0 (2)圖2說明捕食者滅絕, 食餌存在且達到最大環境容納量, 其中r0=0.4,m=0.1,a=0.08,e=1,α=0.01,p=0.4,d=0.35, 注意到m=0.08>0.07=cp(r0-d)/a, 定理4的條件成立, 因而E1是漸近穩定的。 圖2 常值穩態解E1 圖3 正常值穩態解E2 (4)圖4說明捕食者和食餌共存于一個空間齊次周期解, 其中r0=0.4,m=0.3,a=0.01,e=1,α=0.1,p=0.4,d=0.1, 這意味著發生了Hopf分支, 定理6是正確的。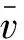
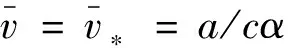
3 數值模擬