Schur定理的推廣

王淑娟， 劉舒暢

(黑龍江大學數學科學學院， 黑龍江哈爾濱150080)

早在1905年，Schur[1]給出一般線性Lie代數交換子代數的極大維數的定理，闡述了兩兩交換矩陣線性無關的極大維數，由此得到有限維交換Lie代數忠實表示的極小維數。Jacobson[2]利用矩陣的相似變換，對Schur定理進行了證明；菲爾茲獎獲得者 Mirzakhani[3]利用分塊矩陣及數學歸納的思想，也對Schur定理進行了證明。文獻[4-7]中利用Jacobson的思想，得到了有限維交換Jordan代數與交換Lie超代數忠實表示的極小維數。 本文中借鑒Mirzakhani的思想， 利用分塊矩陣理論以及數學歸納法， 確定上三角矩陣空間的弱交換空間的極大維數，對Schur定理進行推廣。

1 有關概念

約定基域 F為特征的代數閉域。記M(n, F)為n×n型矩陣全體，其中n為自然數，t(n, F)為n×n型上三角矩陣全體。稱矩陣A,B∈t(n, F)是弱交換的，如果存在與A、B有關的λ∈F, 使得AB=λBA。設V為t(n, F)的一個子空間，若V中任意2個矩陣都是弱交換的, 則V稱是一個弱交換空間。

下面給出Lie代數與Jordan代數的定義。

定義1[4]設L為域 F上的一個代數, 其乘法用[,]表示。若對L于中的任意元素a、b、c都有

[a,b]=-[b,a],[a,[b,c]]=[[a,b],c]+[b,[a,c]]，

則稱為Lie代數。

設M(n, F)中任意2個元素為X、Y，定義

[X，Y]=XY-YX,

則M(n, F)關于新定義的乘法[,]構成一個Lie代數，記為gl (n),稱為一般線性Lie代數。

定義2[4]設J為域 F上的一個代數。若對J于中任意元素x、y都有

xy=yx,(x2y)x=x2(yx) ,

則稱J為Jordan代數。

對于M(n, F)中任意2個元素X、Y定義

X°Y=XY+YX，

則M(n, F)關于新定義的乘法° 構成一個Jordan代數，記為J(n)，稱為特殊Jordan代數。

下面給出Lie代數與Jordan代數的表示的定義。

定義3[8]設L為 F上的Lie代數。若線性映射

φ∶L→gl (n)

為一個Lie代數同態, 即

φ([a,b])=φ(a)φ(b)-φ(b)φ(a) ,

其中a、b為L中任意2個元素，則稱φ為Lie代數L的表示，稱n為表示的維數。進一步, 若φ是單同態的，則稱其為L的忠實表示。

定義4[9]設J為F上的Jordan代數。若線性映射

φ∶J→J(n)

為一個Jordan代數同態, 即

φ(xy)=φ(x)φ(y)+φ(y)φ(x) ,

其中x、y為J中任意2個元素, 則稱φ為Jordan代數J的表示, 稱n為表示的維數。進一步，若φ是單同態的，則稱其為J的忠實表示。

2 主要結果

定理1若V為t(n, F)中具有極大維數的弱交換空間, 則dimV=?n2/4」+1，其中?·」為向下取整函數, dim為空間的維數函數。

證明： 設

F=Span{Eij|1≤i≤?n/2」,?n/2」+1≤j≤n} ,

其中Eij為第i行第j列位置元素為1且其余位置元素全為0的n×n型矩陣，Span表示張成子空間。顯然， F ′=F ?FI是一個弱交換空間且維數為?n2/4」+1, 其中I為單位矩陣, ?為空間的直和運算符。由此，

dimV≥?n2/4」+1 。

下面利用數學歸納法證明dimV≤?n2/4」+1。當n=1時，結論顯然成立。假設結論對于n-1的情形成立，下面考慮n的情形。利用反證法, 假設

dimV>?n2/4」+1,

則t(n, F)包含了一個維數為σ(n)=?n2/4」+2的弱交換空間H。設H的一組基為

{A1,A2, …,Aσ(n)} ，

則存在(n-1)×(n-1)型矩陣Mi, 使得

其中*為矩陣Ai第1行的元素。因為

H=Span{A1,A2, …,Aσ(n)}

是t(n, F)的一個弱交換空間, 所以

W=Span{M1,M2,…,Mσ(n)}

也是t(n-1, F)的一個弱交換空間。記k=dimW，根據歸納假設可知，

k≤?(n-1)2/4」+1 。

不失一般性地, 設M1,M2,…,Mk線性無關,因此

其中mi1,mi2,…,mik∈F,i=k+1,k+2,…,σ(n)。記

則每個Bi具有形狀Bi=[Ti,O]T,其中

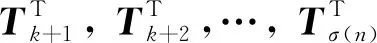
同理, 記

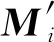
是t(n-1, F)的一個弱交換空間。設r=dimW′，根據歸納假設可知

r≤?(n-1)2/4」+1 。

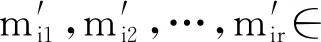
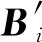
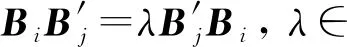
進而可知

其中i=k+1,k+2，…,σ(n)；j=r+1,r+2,…,σ(n)。

設

A=(Tk+1,Tk+2，…,Tσ(n))T，

顯然rankA=σ(n)-k, 其中rank表示求矩陣的秩。設

P={X∈Fn|AX=O} ,

則有dimP=n-rankA。注意到Sr+1,Sr+2,…,Sσ(n)∈P，dimP≥σ(n)-r，因此

n=rankA+dimP≥

(?n2/4」+2-k)+(?n2/4」+2-r)≥

2(?n2/4」-?(n-1)2/4」+1) 。

由此，若n=2q,則2q≥2(q+1)，矛盾；若n=2q+1,則2q+1≥2(q+1)，矛盾。假設不成立，定理1證畢。

定理1涵蓋了文獻[1-4, 7]中的結果, 極大地簡化了文獻[7]中的相關證明, 推廣了Schur的關于兩兩交換矩陣線性無關極大個數的相關定理[2-4]。

需要注意的是，由F ′的結構可知，t(n, F)的一個具有極大維數的弱交換空間的基可取為

{Eij|1≤i≤?n/2」,?n/2」+1≤j≤n}∪{I} 。

推論1一般線性Lie代數gl(n)與特殊Jordan代數J(n)的交換子代數的極大維數分別為?n2/4」+1與?n2/4」。

證明： 設M為gl (n)的任意交換子代數。一方面，由于兩兩交換的矩陣必能同時上三角，因此可以視M為t(n, F)的一個弱交換空間；另一方面，由定理1可知，dimM≤?n2/4」+1。注意到定理1證明中F ′的結構，可知gl (n)的交換子代數的極大維數不小于?n2/4」+1。

由Jacobson弱閉集定理可知, J(n)的交換子代數可以同時嚴格上三角，因此J(n)的任意交換子代數可視為n(n,F)的弱交換空間，其中n(n,F)為全體n×n型嚴格上三角矩陣。設M′為J(n)的具有極大維數的交換子代數，則有

dimM′

否則，M′?FI是維數大于?n2/4」+1的弱交換空間，這與定理1矛盾。注意到在定理1的證明中，F的結構表明dimM′≥?n2/4」。推論1證畢。

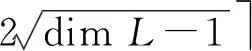
證明： 設φ∶L→gl (n)為Lie代數L的忠實表示，由推論1可知，

設ρ∶J→J(n)是Jordan代數J的忠實表示，由推論1可知，

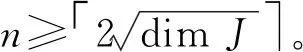
推論2證畢。

推論2給出了任意有限維交換Lie代數與交換Jordan代數的忠實表示的極小維數[3]。

3 結論

本文中利用分塊矩陣理論及數學歸納法，得到了上三角矩陣空間的極大維數，以及一般線性Lie代數與特殊Jordan代數交換子代數的極大維數，并且給出任意有限維交換Lie代數以及交換Jordan代數忠實表示的極小維數，簡化了文獻[7]中相關定理的證明。