具有隨機黏性阻尼的分數維線性振蕩器中的隨機多共振

郭筱瑛 周英姿 王利華 王詩心

( 1. 攀枝花學院智能制造學院 攀枝花 617000 2. 西華大學電氣與電子信息學院 成都 610039）

0 引言

噪聲常被認為對系統輸出信號起負作用，因此人們常采用多種措施來抑制噪聲以提高對有用信號的輸出性能[1-5]；但是，在某些隨機系統中，包括電路和生物傳感器系統等，噪聲可以提升系統對弱信號的檢測能力。隨機共振就是這樣一種當動力系統中存在一定量的噪聲時噪聲會提高系統性能的非線性現象[6-8]。分數維系統具有對歷史狀態記憶的優良特性，因此，系統瞬時狀態可以包含其在時間上的歷史演變過程。分數階系統在許多領域被廣泛研究[9-13]，比如有非黏性的機械過程、記憶效應阻尼效應、摩擦或復合材料響應，以及粘彈性特性模型等。

近年來，分數維系統中的隨機共振得到廣泛的關注。在這些系統中，阻尼采用具有分數導數的記憶核函數進行數學建模。在分數維導數定義中使用的記憶核函數主要有 Gamma函數、負指數函數和Mittag-Leffer函數三種形式。使用 Gamma函數的分數維導數系統已經得到許多學者的廣泛關注[14-24]，用具有 Gamma函數的分數維導數來研究一階分數維過阻尼線性系統的隨機共振機制[14]，分析分數維振蕩器輸出信號的方差與相關函數[15]，研究周期調制噪聲驅動下欠阻尼分數維振蕩器中的隨機共振現象[16-17]，研究加性分數高斯噪聲作用下分數階振蕩器中的隨機共振[18]，研究具有隨機質量的分數振蕩器中的隨機共振[19-20]，研究非線性分數階雙穩系統邏輯隨機共振[21]，研究色噪聲環境下系統記憶性對分數階布朗馬達合作輸運特性的影響[22]，研究帶反饋的分數階耦合布朗馬達的定向輸運[23]等。也有學者將負指數函數作為核函數來分析含時滯反饋與漲落質量的記憶阻尼系統的隨機共振[24]，這里的負指數核函數是作者定義的函數。采用Mittag-Leffler函數的記憶核函數可以表示為[25]，其中τ為系統特征記憶時間，α為分數維數。Eα(?)為Mittag-Leffler函數[26]，在短時間內表現為拉伸指數，在長時間內表現為逆冪律。當τ→0時，記憶核簡化為冪律函數其 中Γ(?)就 是Gamma函數。可見，采用Gamma函數的記憶核函數是采用 Mittag-Leffler函數的記憶核函數的一個特例，而后者更具一般性，特別是其中包含系統特征記憶時間τ，可以在復雜無序的非均勻環境中描述介質分子對系統運動產生的記憶效應。因此采用Mittag-Leffler函數的分數維導數可以從特征記憶時間和分數維數兩個維度更好地刻畫系統的性能。有學者研究了周期外力作用下具有 Mittag-Leffler核函數的通用郎之萬方程描述系統中的隨機共振[27]，但是對具有 Mittag-Leffler核函數的分數維線性系統中的隨機共振研究方面的成果仍然相對較少。

雙值噪聲由于在數學計算上相對簡單，且其極限可產生高斯白噪聲和白脈沖噪聲，因此在分數維線性振蕩器中受到很多關注[14-17,19-20]。另一方面，三值噪聲是一種三級 Markov噪聲，在不同領域也是常用的噪聲模型[28]。對三值噪聲而言，扁平參數可以取1到∞的任意值；而對于對稱雙值噪聲，其扁平參數為 1。可見，相對于雙值噪聲，研究三值噪聲對系統的作用更具一般性，研究分數維振蕩器中三值噪聲的影響具有更廣泛的理論意義。文獻[18-19]分別研究了受三值噪聲擾動的特征頻率和質量的分數維振蕩器中的隨機共振現象，但沒有考慮黏性阻尼的因素。黏性阻尼是多諧振蕩器動力系統的一個重要參數。Chen L.C.等研究了具有線性黏性阻尼和摩擦系數的 Duffing振蕩器的動力行為[29]。有學者研究了具有線性黏性阻尼[30-31]或受雙值噪聲擾動隨機黏性阻尼[16,32]的二階多諧振蕩器中的非線性動力行為。較少文獻關注具有Mittag-Leffler記憶核且黏性阻尼受三值噪聲擾動的分數維振蕩器中的隨機共振效應。基于此，本文研究具有Mittag-Leffler記憶核、受三值噪聲擾動隨機黏性阻尼的分數維線性振蕩器中的隨機共振現象。

1 數學模型

考慮噪聲環境中具有記憶核和隨機黏性阻尼的分數維線性振蕩器，其數學模型由隨機微分方程描述為

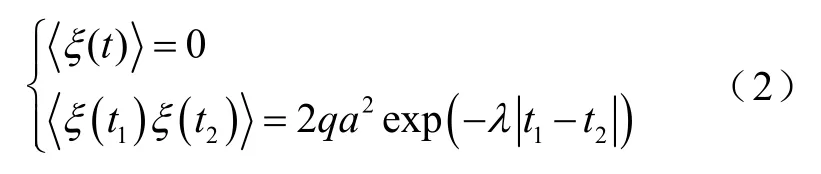
式中，λ為噪聲的相關率；噪聲ξ(t)的扁平率為

根據第二漲落耗散定理[35], 隨機力由相互獨立的熱噪聲η0(t)和ηα(t)兩部分組成，它們都服從均值為零的高斯分布，自相關函數分別為

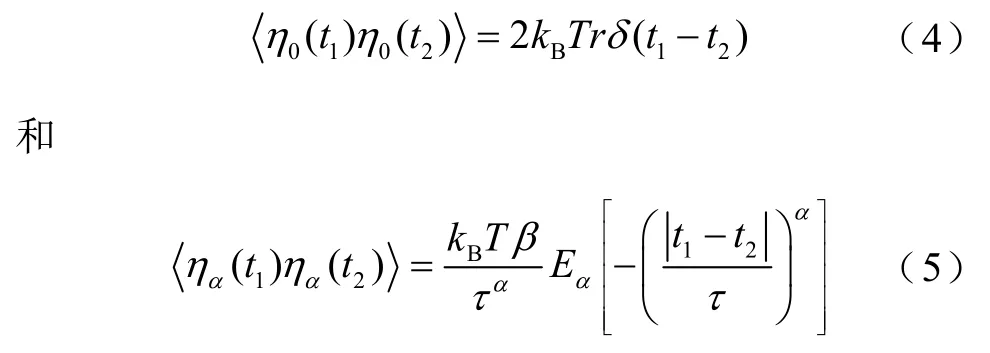
當α=1，相關函數式（5）簡化為指數形式的標準 Orstein-Uhlenbeck過程[36]。值得指出的是，本文研究的振蕩器與參考文獻[27]有所不同。這里考慮了隨機黏性阻尼，而文獻[27]沒有涉及。除了加性噪聲，還考慮了對黏性阻尼和驅動力的擾動，并假設它們都來源于同一干擾源，而在文獻[27]中，僅考慮了加性噪聲。另外，本文的模型與文獻[17]也不同，后者的擾動為雙值噪聲，且記憶核為Gamma函數。一般而言，加性噪聲來源于系統的外部，故與系統態變量無關。從形式上看，系統（1）的阻尼力包含的隨機項ξ(t)為系統態變量與噪聲的乘積，即ξ(t)為乘性噪聲。由于乘性噪聲干擾了系統的結構參數（這里是對阻尼的擾動），導致系統傳輸函數與噪聲參數有關，從而使系統輸出信號是噪聲參數的線性或非線性函數，因此相對于無噪聲的線性系統而言，對系統的求解要復雜一些，有時候可能無法求出其解析解。對于分數維線性系統而言，乘性噪聲的引入，在求解過程中會在時域中出現分數導數與噪聲乘積的數學形式，表達式很復雜，為了求解方便，需要綜合利用微積分、噪聲的性質及變換域（這里是Laplace變換）求解方法，將時域中的復雜方程變換為變換域中的線性方程進行求解，最后再利用反變換域方法求出系統輸出的時域解析解。

本文采用在分數維線性系統的求解過程中廣泛使用的矩方程方法[7,14-20,30-32]，即通過求解系統態變量與噪聲ξ(t)乘積的一階矩滿足的方程來求解平均輸出幅度。對式（1）兩邊取隨機平均，得

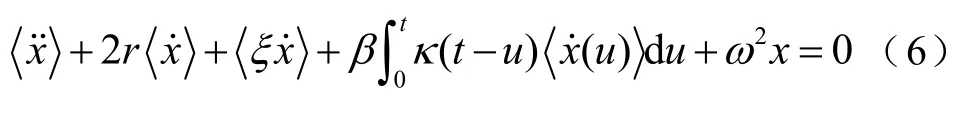
式（1）兩邊同乘以ξ(t),再進行隨機平均，有

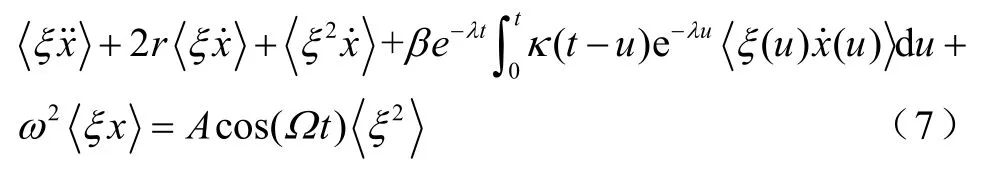
式中，m為ξ(t)的任意函數。令對于關于噪聲與系統態變量乘積的新變量x5、x6，利用式（8）進行處理，同時結合式（6）和式（7），可得

利用三值噪聲的特性[22]和式（8）、式（10），可得

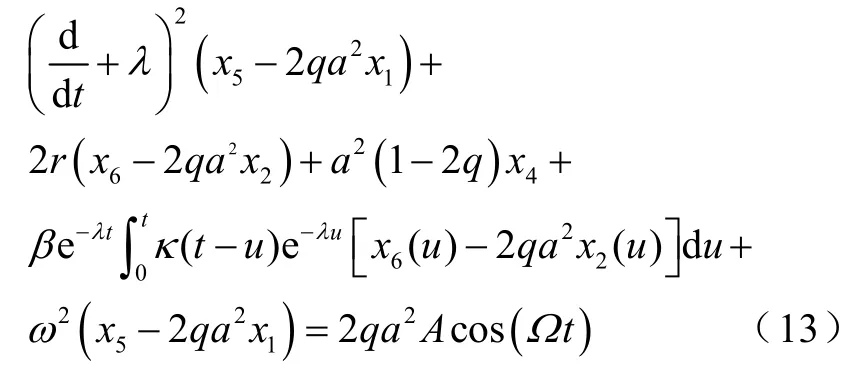
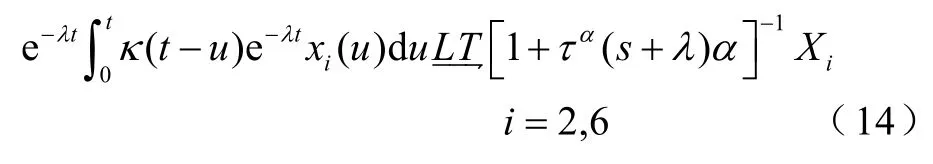
對這些方程進行反拉普拉斯變換，在極限t→∞下，系統的初始狀態的記憶消失，在下面條件下系統有穩態解

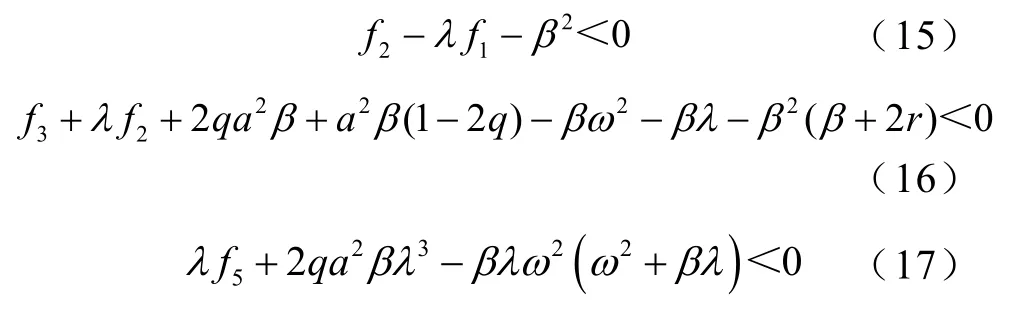
穩態條件下系統輸出幅度（輸出一階矩x(t)）的幅值可求得為

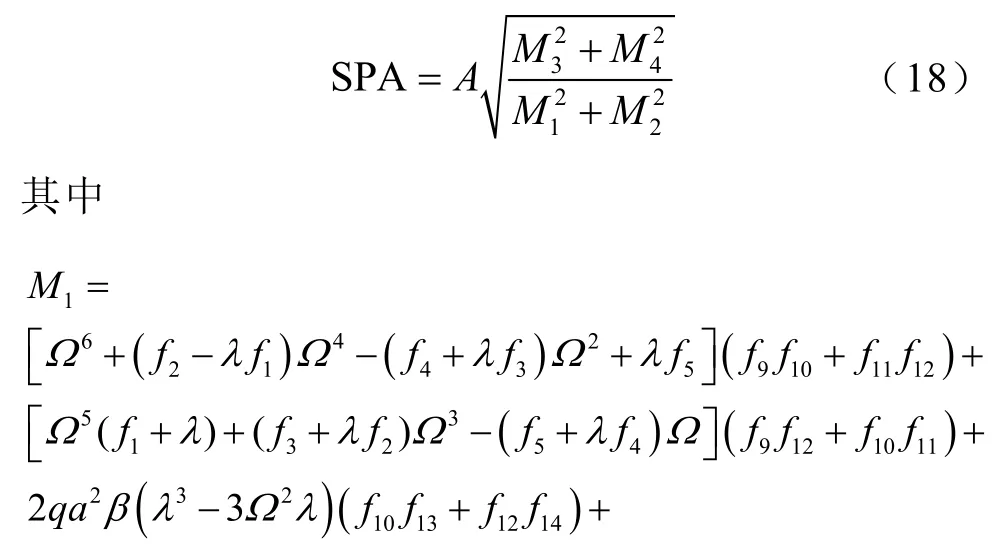
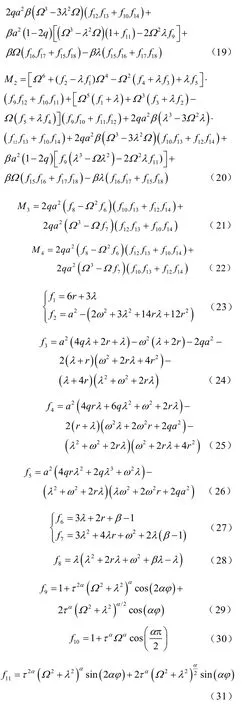
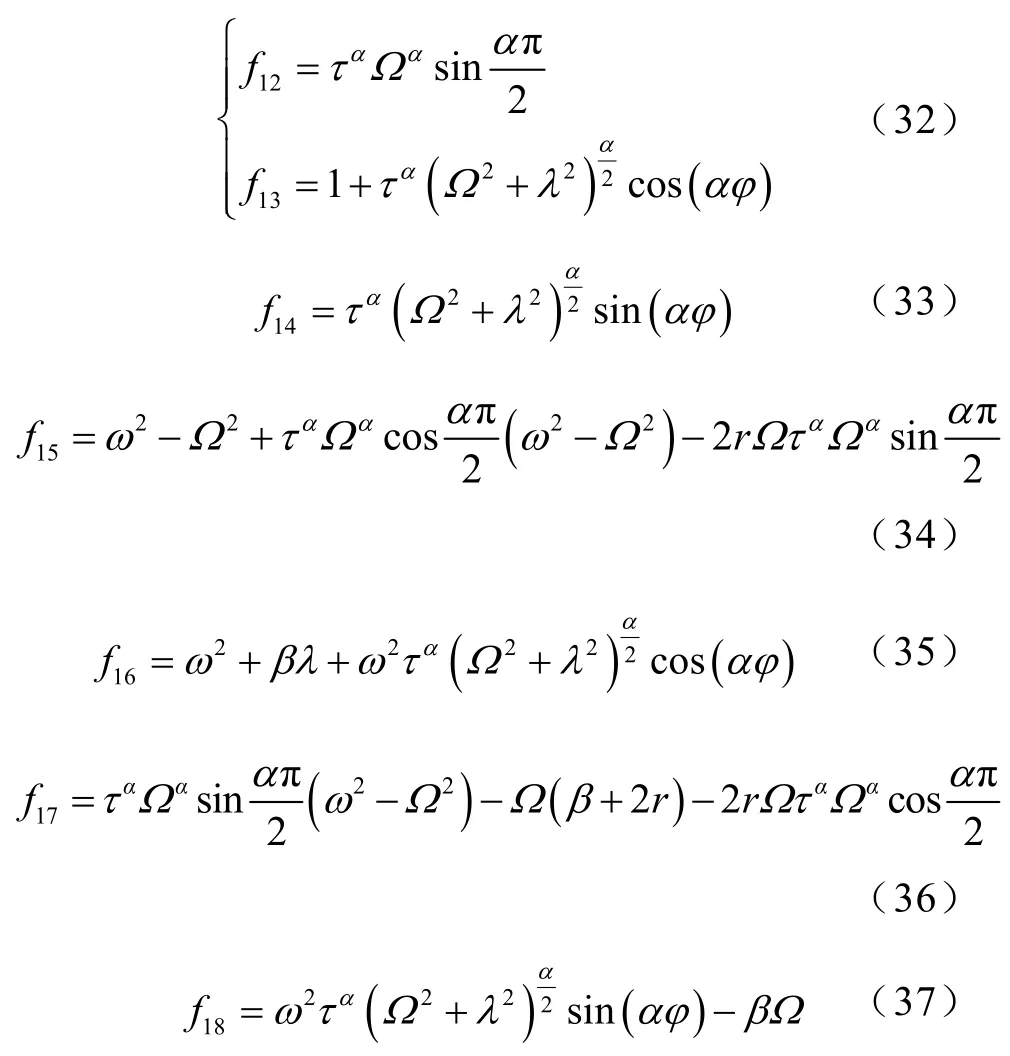
2 隨機共振現象分析

利用式（18）～式（37），得到了系統輸出幅度SPA的解析表達式。下面分析系統參數和三值噪聲參數等對系統輸出幅度的非線性依賴關系。噪聲扁平參數是三值噪聲的一個重要參數，但是對于三值噪聲扁平參數對分數維線性振蕩器的影響研究相對較少。利用圖1～圖3來分析噪聲扁平參數對系統輸出幅度的影響。在圖1～圖3中，橫軸為噪聲的穩態概率q（扁平參數g= 1 /(2q)），指三值噪聲取值為a或-a這個事件發生的頻率，即在考察單位時間內噪聲取值為a或-a的次數。穩態概率大意味著單位時間內三值噪聲取a或-a這兩個值的次數多，而穩態概率小則意味著單位時間內三值噪聲取這兩個值的次數少。縱軸SPA表示穩態條件下系統輸出信號幅度的均值，即系統輸出的一階矩x(t)，它從數理統計的角度來度量系統輸出信號的大小，SPA大（小）表示系統輸出信號的平均幅度高（低）。圖1～圖3是系統輸出信號幅值隨三值噪聲穩態概率變化的關系曲線。由圖 1～圖 3可以看出，在 SPA與穩態概率（扁平參數的倒數，見式（3））的關系曲線上都有一個共振峰，故當其他參數固定時，通過調諧三值噪聲的穩態概率，系統輸出幅值可實現最大化，意味著單位時間內噪聲取值為a或-a的次數/頻率為某個值時，系統輸出幅值可以最佳。由此注意到，在具有三值噪聲擾動阻尼和三值噪聲擾動頻率的分數維線性系統[18]中，發現了系統輸出隨三值噪聲穩態概率變化而出現一個共振峰的現象，而在三值噪聲擾動質量的分數維線性系統[19]中，系統輸出幅度隨三值噪聲穩態概率的變化出現的卻是一個最小值，即反共振現象。可見，三值噪聲擾動的系統參數不同，系統輸出與三值噪聲穩態概率的關系曲線也不同。系統輸出與三值噪聲間的單峰現象在文獻[14-20]中沒有研究。同時，SPA也是三值噪聲的相關率λ、系統頻率ω和驅動力的頻率Ω的非單調函數。由圖1可見，對于較小的概率q(0＜q＜ 0 . 12)，隨著λ的增大，SPA單調減小；而對于較大的概率(q＞0.21)，SPA 隨著λ的增大而增大。SPA對ω和Ω的非線性依賴性可以由圖2和圖3按照類似的方法分析。隨著λ和Ω的增大，峰值朝q值大的方向移動，如圖1和圖3所示；而隨著ω的增大，SPA的峰值朝q值減小的方向運動，如圖2所示。

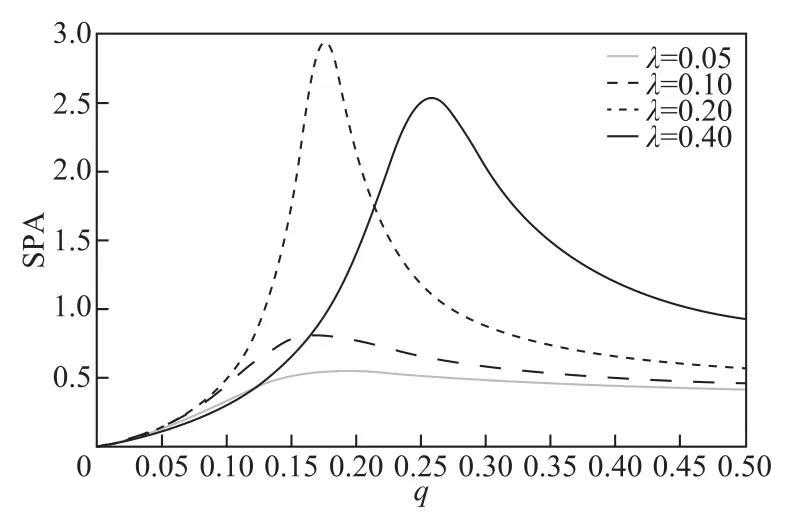
圖1 三值噪聲相關率λ取不同值時系統輸出幅度SPA與三值噪聲穩態概率q的關系曲線，其他參數為r=0.8,a=1 .9,ω=1.2,β=0.3,τ=1,α = 0 .05,Ω=1,A=1Fig.1 The output amplitude SPA versus the stationary probability q of the trichotomous noise for r=0.8,a=1.9,ω=1 .2,β=0.3,τ=1,α = 0.05,Ω=1,A=1 for different values of the correlation rate λ of the trichotomous noise

圖2 系統頻率ω取不同值時系統輸出幅度SPA與三值噪聲穩態概率q的關系曲線，其他參數為r=0.8,λ= 0 .2,a=1.9,β=0.3,τ=1,α=0.05,Ω=1,A=1Fig.2 The output amplitude SPA versus the stationary probability q of the trichotomous noise for r=0.8,λ= 0 .2,a=1.9,β=0.3,τ=1,α=0.05,Ω=1,A=1 for different values of the system frequency ω

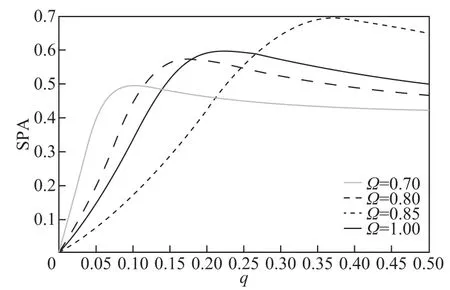
圖3 驅動信號頻率Ω取不同值時SPA與三值噪聲穩態概率q的關系曲線，其他參數為r=0.8,λ=0.2,a=2,ω=0 .9,β=0.3,τ=1,α=0.05,A=1Fig.3 The output amplitude SPA versus the stationary probability q of the trichotomous noise for r=0.8,λ= 0 .2,a=2,ω=0.9,β=0.3,τ=1,α=0.05,A=1 for different values of the frequency Ω of the driving force

需要說明的是，在分析系統輸出幅度SPA隨著某個參數y變化是否存在隨機共振現象時，是基于SPA對y的函數極值這個條件來進行的，即對偏導數 ? ( SPA)/?y= 0 這個等式，看是否存在y值或有幾個y值可以使該等式成立。由式（18）～式（37）可見，SPA是系統參數、噪聲參數、輸入信號參數等多個參數的復雜非線性函數，因此，對于不同的參數y（對于本文而言y指噪聲穩態概率q、黏性阻尼r和系統特征記憶時間τ），使 ? ( SPA)/?y= 0 成立的其他參數需要滿足的條件可能也不同，因此，在研究 SPA與不同參數曲線上出現共振現象時，同一個參數的取值可能也不同。現在來分析SPA與黏性阻尼r的關系。由圖4～圖6可以看出，在SPA與r的關系曲線上存在兩個極值。隨著r的增大，SPA先取一個最小值然后取最大值。而在雙值噪聲擾動的隨機黏性阻尼、具有Gamma函數記憶核函數的分數維線性系統[17]中，在輸出幅度隨黏性阻尼的變化曲線上存在三個極值。可見，由于對黏性阻尼的擾動噪聲不同，系統輸出幅度隨黏性阻尼變化的非單調行為也不同。另外，本文觀察到的與黏性阻尼間的非單調依賴關系與文獻[38]研究的具有擾動頻率整數階諧振器中出現的現象類似，而在分數維線性振蕩器[14-16,18-19]中沒有研究該現象。另外，由圖4可見，隨著β的增大，SPA的極值由兩個變為一個，峰值朝r值減小的方向移動。比較圖4與圖5、圖6發現，隨著λ和Ω的增大，SPA的峰值不是朝著一個方向移動，SPA 先移向r值減小方向，后又朝r值增大方向移動；如圖4所示，隨著β的增大，SPA的峰值僅朝著一個方向移動，即朝著小的r值方向移動。

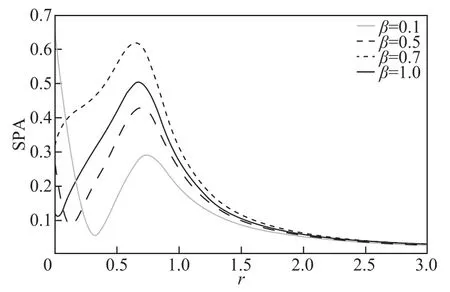
圖4 摩擦系數β取不同值時SPA與黏性阻尼r的關系曲線，其他參數為λ=0.3,a=1,ω=0.6,q=0.2,τ=10,α= 0.9,Ω=1,A=1Fig.4 The output amplitude SPA versus the viscous damping r for λ=0.3,a=1,ω=0.6,q=0.2,τ=10,α=0.9,Ω=1,A= 1 for different values of the friction coefficient β

圖5 三值噪聲相關率λ取不同值時SPA與黏性阻尼r的關系曲線，其他參數為a=0.5,ω=0.5,q=0.2,β=0.3,τ=1 0,α=0.9,Ω = 1 ,A=1Fig.5 The output amplitude SPA versus the viscous damping r for a=0.5,ω=0.5,q=0.2,β=0.3,τ=10,α= 0 .9,Ω=1,A=1 for different values of the correlation rate λ of the trichotomous noise

圖6 驅動力頻率Ω取不同值時SPA域黏性阻尼r的關系曲線，其他參數為λ=0.1,a=1,ω=0.5,q=0.2,β=0.3,τ= 1 0,α=0.9,A=1Fig.6. The output amplitude SPA versus the viscous damping r for λ=0.1,a=1,ω=0.5,q=0.2,β=0.3,τ=10,α= 0 .9,A=1 for different values of the frequency Ω of the driving force

記憶功能是分數振蕩器的重要特征[12-13]，由于其記憶特性，分數維振蕩器可以包含以前狀態的動態記憶。在工程系統中，記憶效應和附加特性（例如，非線性）是一種很常見的滯后源[9]。因此，研究分數維振蕩器的記憶特性具有重要的意義。圖7～圖9所示為SPA與系統記憶時間τ的非單調關系。從圖7～圖9容易看出，在每條SPA曲線上，在較小的和中間的記憶時間τ時都呈現出雙峰現象，即出現典型的隨機多共振現象。隨著τ的增大，SPA增大直到取得第一個最大值，然后單調減小直到一個最小值，接著增大到第二個峰值，最后單調減小。值得指出的是，在文獻[27]中，三值噪聲擾動的是系統特征頻率，而本文中三值噪聲作為對系統黏性阻尼的擾動，雖然它們都具有Mittag-Leffler形式的摩擦記憶核函數，但是在文獻[27]中，系統輸出幅值隨記憶時間的變化僅僅出現單峰現象。可見，同樣是三值噪聲，由于其擾動作用的系統參數不同，系統輸出幅度與記憶核的記憶時間變化曲線也不一樣。另外，雖然文獻[24]也研究了特征記憶時間對系統輸出幅度的影響，但沒有發現單峰現象，同時，本文發現的系統輸出與記憶時間的非單調依賴關系在文獻[14-20]中沒有研究過。通過分析圖7可以發現，SPA也是β的非線性函數。隨著β增大SPA兩最大值之間的時間差變小；而隨著λ的增大，SPA的第一個峰值增加緩慢，第二個峰值減小非常快，兩最大值間的差值變長，如圖8所示。故對于較小的記憶時間（τ＜0.08），大的噪聲相關率λ有利于系統輸出性能的提高，而對于較大的記憶時間（τ＞1.2），小的λ能提高系統輸出信號。而且，由圖9可以看出，驅動信號頻率越高（Ω＞1.9），SPA輸出幅度越大。因此高的驅動信號頻率可以提升分數維振蕩器的系統輸出性能。

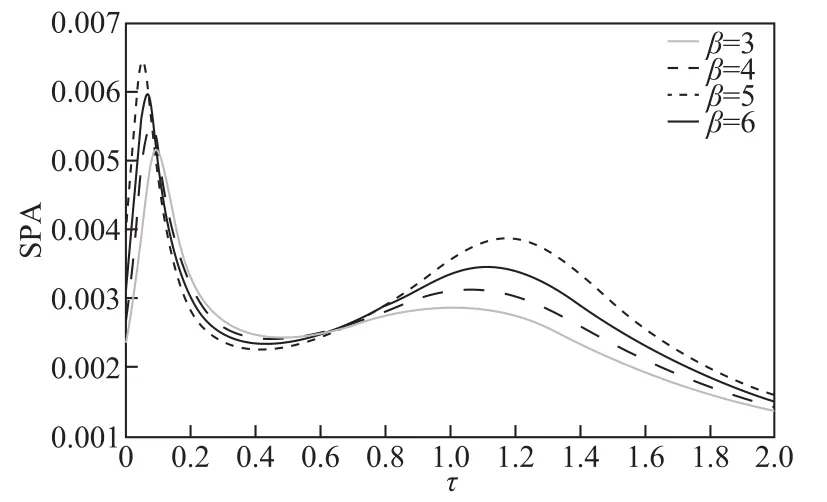
圖7 摩擦系數β取不同值時SPA與系統特征記憶時間τ的關系曲線，其他參數為r=0.5,λ=0.1,a=2,ω=10,q=0 .2,α=0.9,Ω=2,A=1Fig.7 The output amplitude SPA versus the characteristic memory time τ of the system for r=0.5,λ=0.1,a=2,ω=1 0,q=0.2,α=0.9,Ω=2,A=1 for different values of the friction coefficient β

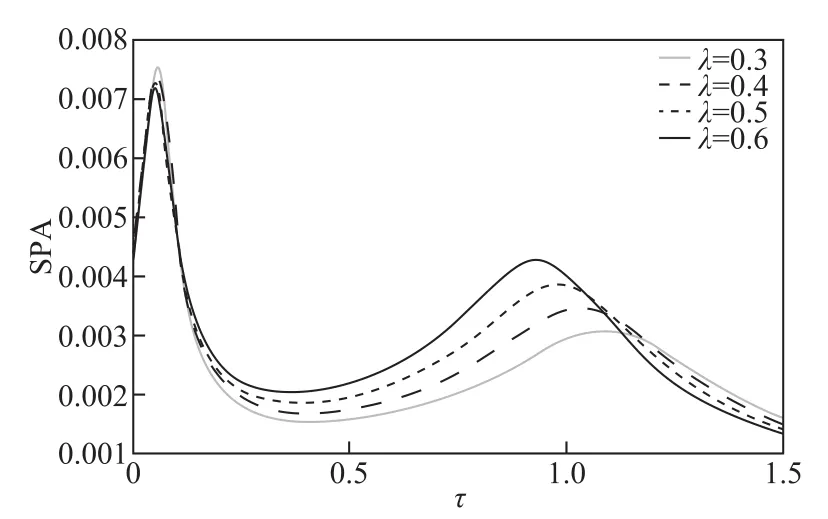
圖8 三值噪聲相關率λ取不同值時SPA與系統特征記憶時間τ的關系曲線，其他參數為r=0.5,a=2,ω=10,q=0 .2,β=2,α=0.95,Ω=2,A=1Fig.8 The output amplitude SPA versus the characteristic memory time τ of the system for r=0.5,a=2,ω=10,q=0 .2,β=2,α=0.95,Ω=2,A=1 for different values of the correlation rate λ of the trichotomous noise

圖9 驅動力頻率Ω取不同值時SPA與系統記憶時間τ的關系曲線，其他參數為r=0.5,λ=0.5,a=2,ω=9,q=0 .2,β=5,α=0.9,A=1Fig.9 The output amplitude SPA versus the characteristic memory time τ of the system for r=0.5,λ=0.5,a=2,ω= 9 ,q=0.2,β=5,α=0.9,A=1 for different values of the frequency Ω of the driving force

3 結論

綜上所述，本文研究了具有隨機黏性阻尼系數和Mittag-Leffler形式核函數、乘性三值噪聲作用下分數維線性振蕩器中的隨機共振現象。分析了噪聲扁平率和系統記憶時間對 SPA的影響。利用Shapiro-Loginov公式和Laplace變換，推導出系統穩態輸出幅度SPA的表達式。在SPA與噪聲穩態概率曲線上，出現一個極值（最大值），在SPA與黏性阻尼和系統記憶時間的關系曲線上，分別呈現兩個極值（一個極小、一個極大值）和三個極值（一個極小值，兩個極大值），即觀察到了隨機共振和隨機多共振現象。由于三值噪聲和分數維振蕩器記憶時間在工程中應用廣泛，本文取得的結果對于分數維振蕩器中的隨機共振研究具有普遍和重要的理論價值。