LCC-MMC型混合直流配電系統線路保護方案

賈 科 馮 濤 陳 淼 王聰博 畢天姝

（新能源電力系統國家重點實驗室（華北電力大學） 北京 102206）

0 引言

電網換相換流器（Line Commutated Converter,LCC）已經在直流輸電系統[1-2]和牽引配電系統[3]中成功應用，由于受端LCC換相失敗[4]問題難以解決，而模塊化多電平換流器（Modular Multilevel Converter,MMC）不存在換相失敗問題[5]，所以基于 LCC和MMC混合換流器的多端直流輸配電可能成為未來直流電網的發展趨勢。現有直流輸電工程已經有混合換流器拓撲結構，給未來直流配電網的發展提供了理論基礎。相比于已經建成的柔性直流配電系統[6]，LCC-MMC型混合直流配電系統建設成本低，耐受暫態沖擊電流能力較強，利用MMC控制電流雙向流動的特點實現配網靈活性。然而直流故障發展迅速，可靠且有選擇的保護原理亟待研究。

實際直流工程廣泛采用閉鎖換流器實現故障電流自清除和直流故障隔離[7]，保護系統設備不受過電流的破壞。傳統LCC直流工程主要通過移相方式[8]，迅速將整流站觸發延遲角移相到90°以上，使得整流站轉變為逆變運行模式[9]，向交流系統釋放儲存的能量，降低故障電流。MMC柔性直流配電工程通過向換流閥發送閉鎖信號，閉鎖換流器切斷故障電流回路，隔離直流故障[10]。然而，故障后快速

閉鎖換流器會導致提供給保護的有效故障信息減少、特征量單一，給傳統直流線路保護的可靠性和選擇性帶來挑戰。

現有直流系統線路保護根據故障檢測的方式可以分為被動保護和主動保護。被動保護利用線路電氣量的變化檢測故障的發生[11]。文獻[12]通過分析故障距離與故障電流之間的反比關系構建電流反時限保護，出口速度快，但故障電流波動影響保護的可靠性。文獻[13]通過小波變換提取故障高頻信息，結合系統高頻阻抗模型構建高頻距離保護。文獻[14]采用低通濾波器處理線路兩端測量電壓和電流，利用線性分布的沿線電壓求解沿線分布電容電流實現故障選極。文獻[15]利用 Prony算法分析線路兩端的電流固有頻率，根據電流固有頻率的差異性特征實現區內外故障識別，但是暫態衰減分量和換流器閉鎖的干擾作用使得電流固有頻率的提取存在一定的誤差。

主動保護[16]通過主動控制電力電子變換器或注入附加信號檢測故障的發生。文獻[17]通過控制MMC子模塊短時間的切出得到低壓脈沖，利用低壓脈沖在檢測點和故障點之間傳播的時間差計算故障距離實現快速保護，但是脈沖陡度過大和持續時間過長易造成正常運行時電壓跌落。文獻[18]通過在 DC-DC控制器中增加信號處理環節檢測直流故障的發生，通過脈寬調制來控制變換器開關的開斷并發送故障信息給保護。文獻[19]通過投入附加裝置，利用附加裝置注入的特征信號確定故障區段，不受故障暫態量的影響，但是難以區分故障邊界，需要采用額外裝置，經濟性受到制約。

因此，鑒于現有的被動保護存在故障邊界模糊、保護性能受限于暫態分量波動和主動保護經濟性較差的不足，本文在概述LCC-MMC型混合直流配電系統拓撲結構及其雙極短路故障特征的基礎上，提出一種基于 LCC注入故障電流的混合直流配電系統被動保護。利用LCC提供穩態故障電流，結合線路兩端電流方向的差異識別區內外故障，解決了故障邊界模糊的問題，基于LCC提供的穩態故障電流幅值比進行故障精確定位，無需注入附加信號，經濟性好。最后在 PSCAD/EMTDC仿真平臺上搭建LCC-MMC型混合直流配電系統仿真模型，驗證了所提保護的有效性和可靠性。

1 LCC-MMC型直流配電系統故障特性

1.1 拓撲結構

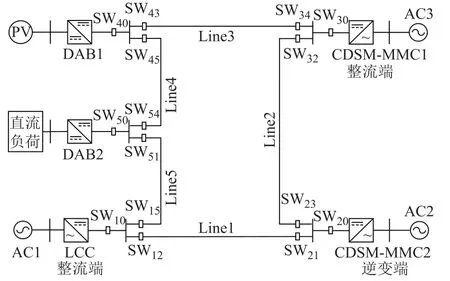
圖1 五端LCC-MMC型直流配電系統拓撲圖Fig.1 Topology of five-terminal LCC-MMC type DC power distribution system

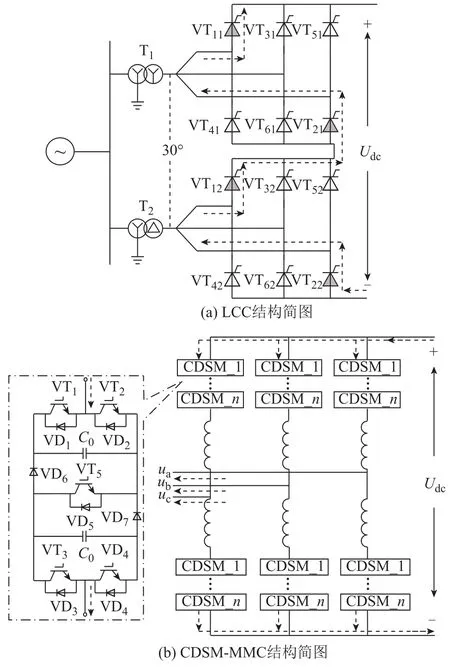
圖2 LCC和CDSM-MMC結構簡圖Fig.2 Structure diagrams of LCC and CDS M-MMC

以現有的廣州直流供電系統[20]、貴州五端柔性直流配電系統[21]和張北柔性直流配電系統[22]工程為例，在PSCAD上搭建的五端LCC-MMC型混合直流配電系統如圖1所示。LCC采用12脈動換流器結構，由兩個6脈動換流器組成，兩個6脈動換流器交流側的相位差30°，拓撲結構如圖2a所示。MMC為具有故障電流自清除能力的鉗位雙子模塊的模塊化多電平換流器（Clamp Double Sub-Module based Module Multilevel Converter, CDSM-MMC），子模塊拓撲結構如圖2b所示。整流側為LCC和CDSM-MMC1，逆變側為 CDSM-MMC2。整流側LCC采用定直流電流控制，CDSM-MMC1采用定直流電壓控制。逆變側CDSM-MMC2采用定有功功率控制。光伏和直流負荷經雙有源全橋變換器（Dual Active Bridge, DAB）直流變壓器與直流系統連接，控制方式為單移相控制。直流線路額定電壓等級為±10kV，DAB通過占空比控制低壓側電壓為750V，接地方式為交流側高阻接地[23]。當直流線路發生雙極短路故障后，換流器 CDSM-MMC1、CDSMMMC2、DAB1和DAB2閉鎖，LCC采用不閉鎖方式。在LCC定直流電流控制器限幅環節的作用下，觸發延遲角趨于穩定，LCC注入的故障電流最終趨于穩定值，系統進入故障穩態階段。由于故障后CDSM-MMC和DAB直流變壓器閉鎖，系統中負荷被切除，因此不考慮因電壓跌落而無法滿足負荷運行的問題。

LCC-MMC型混合直流配電系統的主電源通過LCC輸出功率，其他輔助電源利用CDSM-MMC能夠控制潮流雙向流動的特點實現系統功率調節。在建的直流配電工程采用電纜線路供電，接地方式為高阻接地，單極接地故障和斷線故障不會引起嚴重過電流，極間電壓不會突變，因此本文的研究主要針對雙極短路故障。

1.2 故障特征

雙極短路故障發生后，CDSM-MMC和DAB直流電容迅速放電造成過電流，故障電流達到 IGBT耐受電流能力時，CDSM-MMC和DAB直流變壓器閉鎖[24]，系統僅剩下LCC向故障點饋入故障電流，系統進入故障穩態階段，LCC提供故障穩態電流。根據換流器的工作狀態，整個故障過程可以分為兩個部分：閉鎖前和閉鎖后[25]。閉鎖前主要為換流器中直流電容放電過程[26]，放電回路如圖3所示。圖中Ceq為故障時直流側等值電容，Req和Leq為故障回路等值電阻和故障回路等值電感。

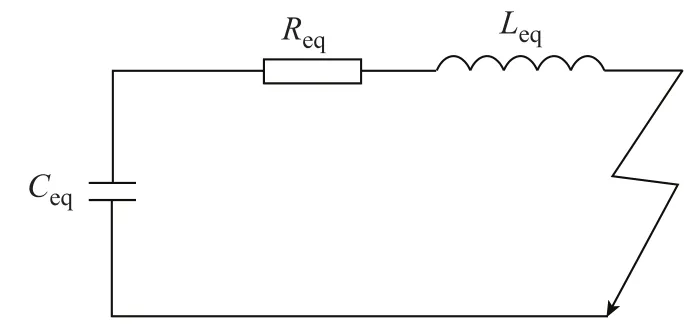
圖3 電容放電回路Fig.3 Capacitor discharge circuit

實際系統中，電容放電回路的等值電阻Req遠小于因此閉鎖前直流電容的放電過程為一個二階欠阻尼振蕩衰減過程[27]。根據圖3可以解析得到直流電容的放電電流為

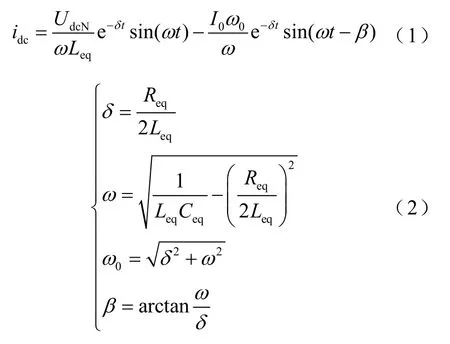
式中，UdcN為直流線路額定電壓；I0為故障時刻直流電流瞬時值。

當考慮平波電抗器和LCC直流出口濾波器時，圖3中的等值電容Ceq和等值電感Leq將會改變，對應式（1）中的δ、ω0、ω和β變化，主要影響放電電流的時間常數和峰值。由于直流配電系統慣性環節少、阻尼小[28]，故障發展迅速，平波電抗器使得保護裝置有更多的時間來響應。

閉鎖后階段，LCC仍然依靠晶閘管兩端交流線電壓過零點自然換相，根據晶閘管的導通條件可知，LCC閥臂仍按照自然換相規則導通（詳見圖4a）。

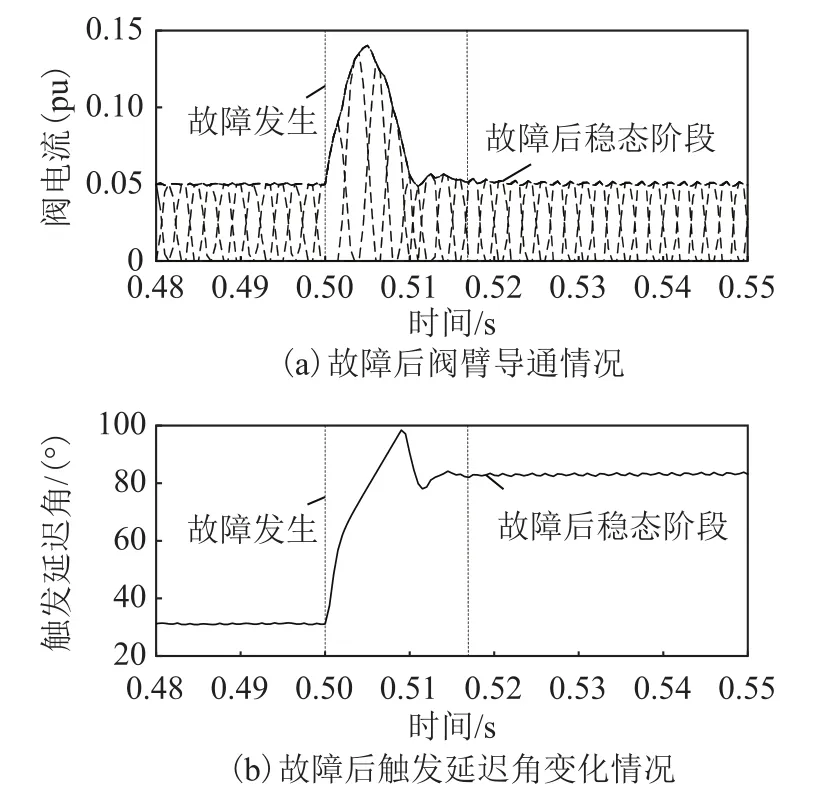
圖4 故障后閥臂導通和觸發延遲角變化情況Fig.4 Schematic diagram of valve arms and firing angle change after a fault

隨著LCC直流出口極間電壓逐漸降低，LCC觸發延遲角增大（詳見圖 4b），此時系統進入故障穩態階段，LCC整流器直流出口電壓為[29]

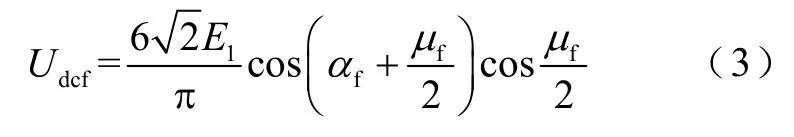
式中，E1為 LCC閥交流側母線線電壓；αf為故障穩態LCC觸發延遲角；μf為故障穩態LCC換相重疊角。

根據上、下單橋的工作方式可知，在一個工頻周期內，上、下單橋各換相6次，在交流側相位相差30°的基礎上，LCC直流出口電壓脈動12次，如圖5所示。

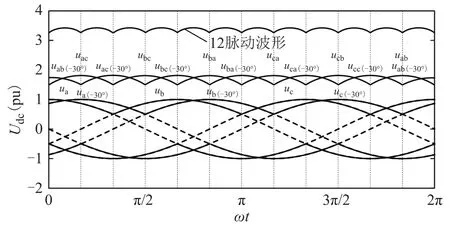
圖5 LCC整流器直流出口電壓波形Fig.5 DC outlet voltage waveforms of rectifier LCC

從圖5可以看出，LCC注入的穩定故障電流含12m(m為正整數）次特征諧波。由于LCC直流出口一般裝有特征諧波濾波器[30]，因此在 CDSM-MMC和 DAB直流變壓器閉鎖后的故障穩態階段，可以近似認為LCC注入到故障點的電流為直流電流，僅與故障回路電阻有關。結合式（3），閉鎖后的穩態階段，LCC注入的穩態故障電流為

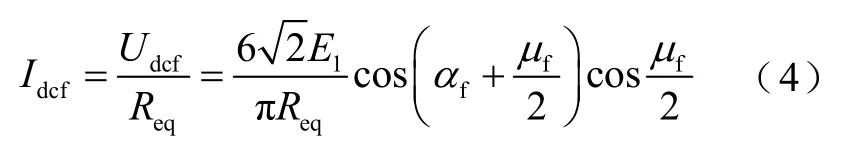
2 保護新原理

2.1 區內外故障識別

根據上面分析可知，CDSM-MMC和DAB直流變壓器閉鎖后，LCC經直流線路向故障點饋入故障電流，且為直流電流，故障回路示意圖如圖6所示。假定雙極短路故障F發生在Line2上，故障電流回路有回路15（以隔離開關SW15為出發點，正負極線路與故障點形成回路）和回路12（以隔離開關SW12為出發點，正負極線路與故障點形成回路），p代表正極線路，n代表負極線路，Idcijp為隔離開關SWij處安裝的保護測量的正極故障電流（i≠j，i=1,2,3,4,5，j=1,2,3,4,5），“+”和“-”分別代表電流方向為正和負。在此規定，由母線流向被保護線路為電流正方向。

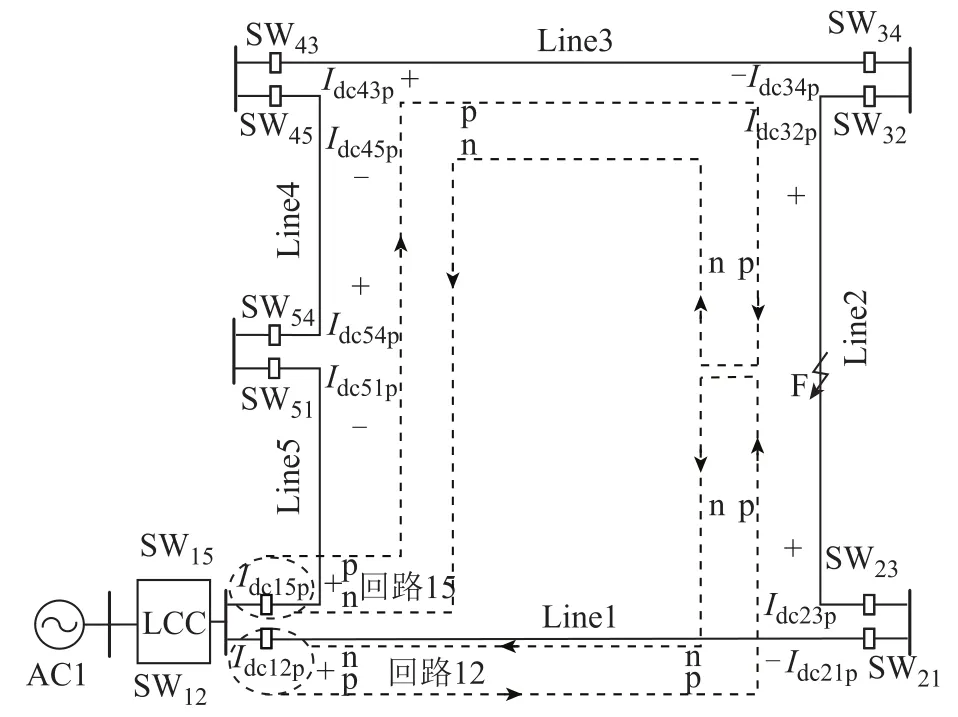
圖6 閉鎖后故障回路示意圖Fig.6 Fault circuit diagram after blocking

定義k為線路兩端正極故障電流比，表達式為

根據圖6可知，故障線路Line2兩端正極電流方向均為正方向，非故障線路兩端正極電流大小相等，方向相反。因此故障線路兩端正極電流比值大于零，非故障線路兩端正極電流比值為-1。因此，可得故障識別判據為

當線路兩端正極電流比值滿足式（6）時，認為發生區內故障；當線路兩端正極電流比值不滿足式（6）時，則認為發生區外故障。

2.2 故障定位

結合圖6，從LCC端口出發，LCC-MMC型直流配電系統故障回路各級線路阻抗均與 LCC端口串聯，故障距離簡要示意圖如圖 7所示。圖中，x2為故障回路15的故障距離，x1為故障回路12的故障距離，x為環網線路總長度，R15、R12分別為故障回路15和故障回路12的單極線路總電阻，Rf為過渡電阻，Udcf為故障后LCC出口極間電壓，Uf為故障點極間電壓。

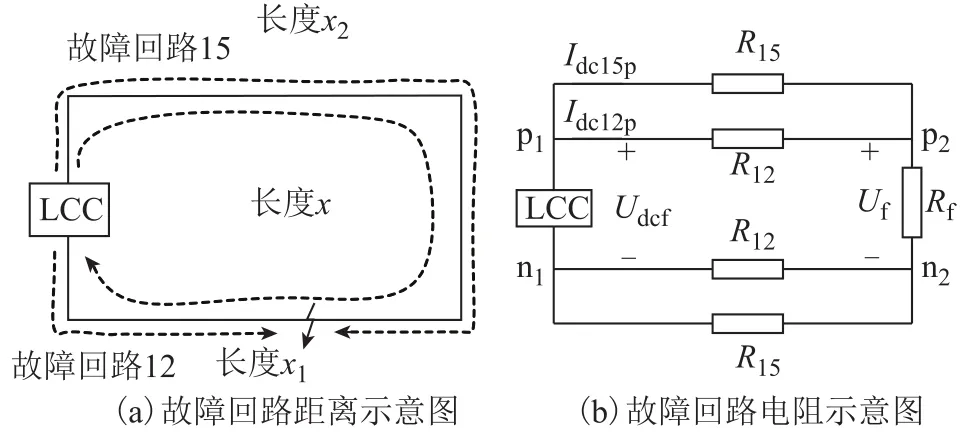
圖7 故障電流回路簡圖Fig.7 Diagram of fault current loop

根據環網拓撲結構可知，整個LCC-MMC型直流配電網的線路總長度x已知。根據圖7a可知，故障回路15和故障回路12的故障距離與系統環網總長度的關系為

根據圖7b可知，故障回路15和故障回路12的正極線路故障電流為

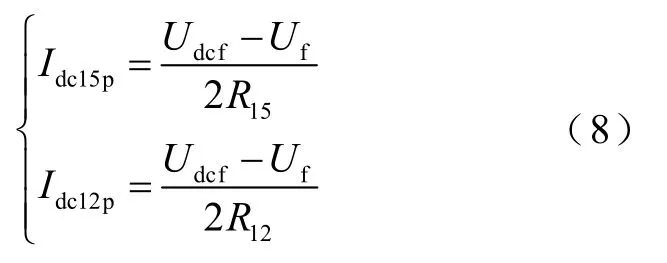
根據圖6可知，故障回路15和故障回路12均是直流線路的簡單串聯，因此故障回路15中故障線路正極電流Idc32p等于LCC出口正極電流Idc15p，故障回路12中故障線路正極電流Idc23p等于LCC出口正極電流Idc12p。于是故障線路Line2的正極故障電流比k為

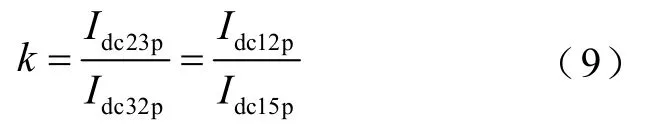
結合式（8）和式（9），可以推出正極故障電流比k為

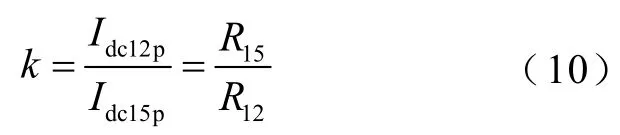
由式（10）可知，k與過渡電阻Rf無關，僅與故障回路15和故障回路12的總回路電阻R15和R12有關。

由于LCC-MMC型混合直流配電系統線路阻抗均勻分布，因此可以得出

式中，r0為線路單位長度電阻值。

結合式（10）和式（11）有

聯立式（7）和式（12）有

由式（13）可以求解得出故障距離x1為

2.3 保護流程

本文所提保護方案如圖8所示，該保護方案由保護啟動、區內外故障識別和故障定位三部分組成。保護啟動過程配置di/dt作為啟動判據。保護裝置啟動后，當故障電流達到 IGBT耐流能力時，閉鎖CDSM-MMC和DAB直流變壓器，利用線路兩端故障電流比k實現區內外故障識別。工業換流器動態調節時間一般為30ms[31]，結合大量仿真數據，本文設置硬延時t=30ms確保故障進入穩態階段，結合式（14），利用穩態數據實現故障精確定位。

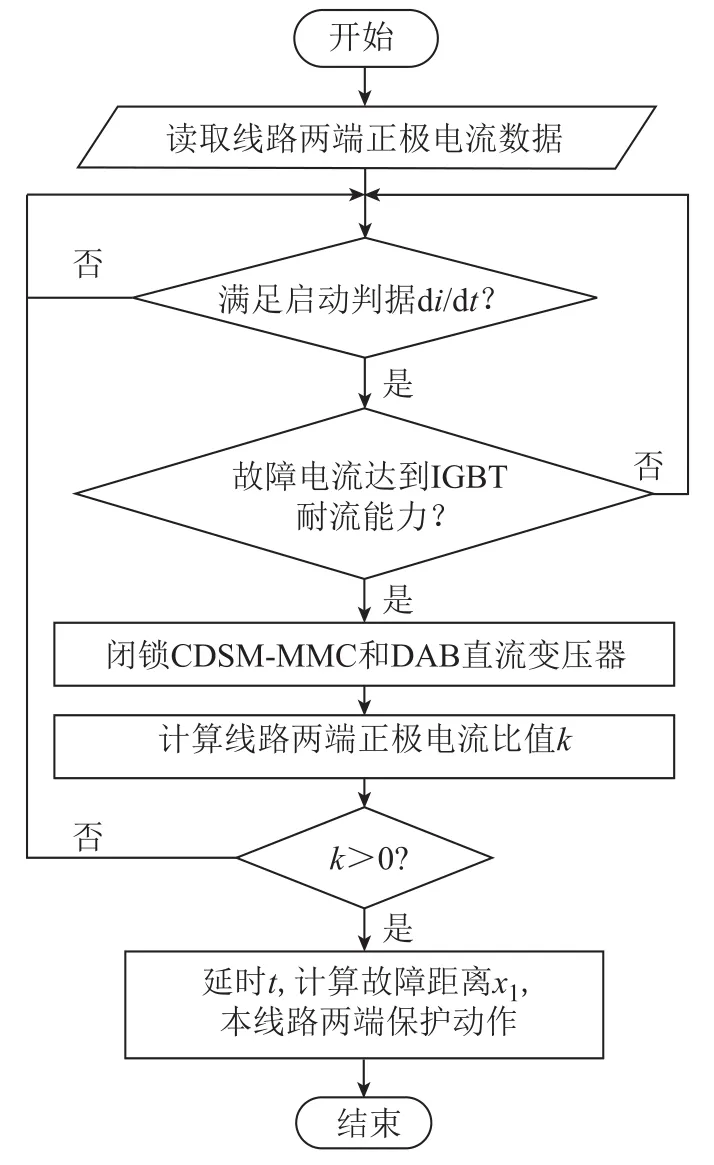
圖8 保護方案流程Fig.8 Flow chart of protection scheme

3 仿真驗證

利用 PSCAD/EMTDC電磁暫態仿真平臺搭建如圖1所示LCC-MMC型混合直流配電系統的仿真模型。直流電纜采用分布參數模型，電纜長度均為3.5km，單位電阻為0.066 9Ω/km，單位電感為0.685 7mH/km，單位單極對地電容為 0.35μF/km，具體參數詳見附表1和附表2，保護裝置采樣頻率為10kHz。

3.1 故障識別與檢測

以 Line1為例，分析區內故障和區外故障時Line1兩端正極故障電流比k的取值情況，仿真結果如圖 9所示，故障發生時刻為 0.5s。LCC-MMC型混合直流配電系統發生雙極短路故障后，閉鎖CDSM-MMC和 DAB直流變壓器，LCC注入的故障電流回路為RL回路，從圖9a可以看出，故障發生12ms后，系統進入故障穩態狀態，此時Line2兩端正極電流比k為穩定值，表明故障穩態電流為穩定的直流電流。

根據圖9a可以看出，當發生區內故障時，Line2兩端正極電流比k＞0，滿足故障識別判據（詳見式（6））。從圖9b可以看出，當區外故障發生時，Line2兩端正極電流比k=-1＜0，不滿足故障識別判據（詳見式（6））。因此，本文提出的故障識別判據可以準確識別區內外故障，無需進行數值整定，就能可靠區分故障邊界。

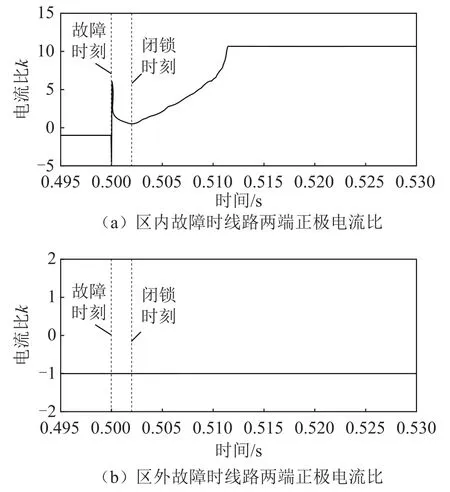
圖9 區內外故障識別Fig.9 Fault identification in and outside the area

3.2 故障定位驗證

3.2.1 故障定位的性能

分別以 Line1、Line2、Line3、Line4和 Line5不同位置故障為例分析所提保護方案進行故障定位的性能，仿真結果如圖10所示。故障距離（故障位置）均為式（14）中的x1，即故障點到 LCC直流出口SW12的故障距離。從圖10可以看出，雙極短路故障發生在不同線路不同位置時，利用 CDSM-MMC和DAB直流變壓器閉鎖后20～30ms內LCC注入的穩態故障電流得到的故障定位結果趨于穩定，穩態誤差均小于1%。

圖10 不同故障位置定位仿真結果Fig.10 Fault location simulation results of different fault positions

統計不同故障位置定位的仿真結果見表 1。表中位置系數為某一線路上的故障點到該線路首端的距離占該線路長度的百分比，計算距離為利用所提保護算法求解得到的故障距離。

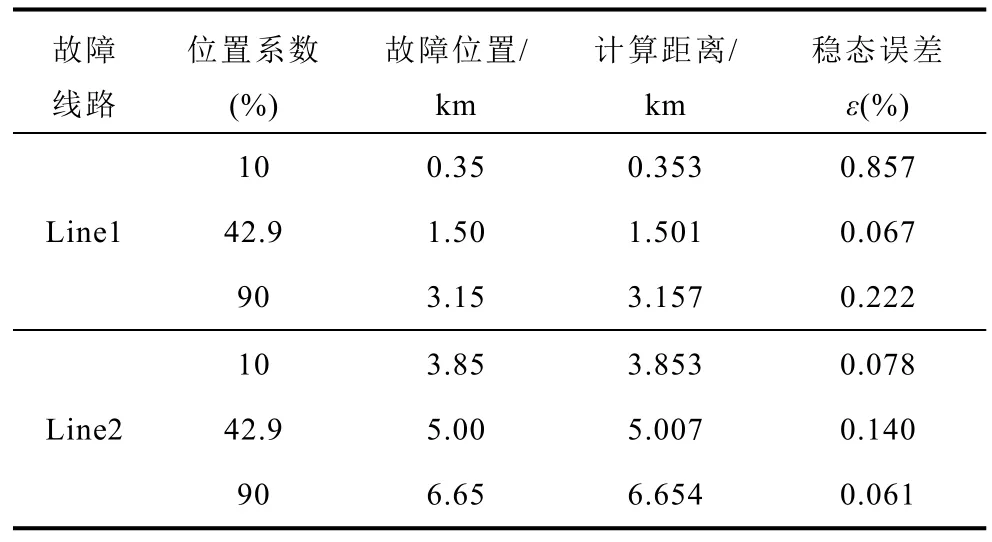
表1 不同位置故障定位仿真結果Tab.1 Fault location results at different fault positions

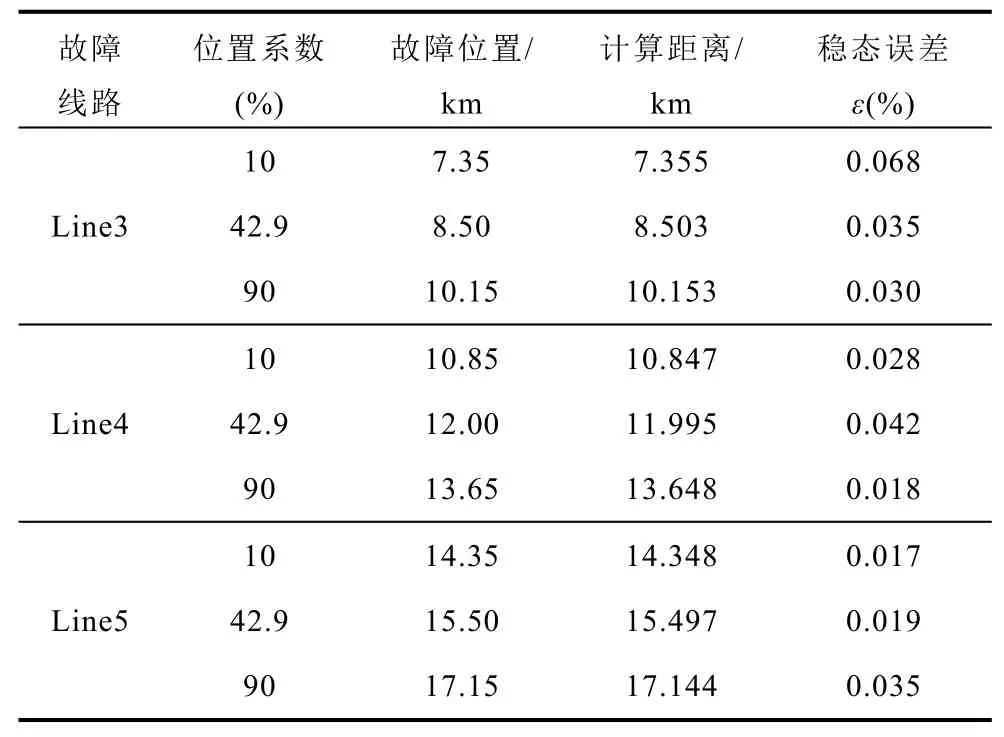
（續）

根據表1中結果可以看出，在LCC-MMC型混合直流配電系統中，Line1、Line2、Line3、Line4和Line5分別設置故障位置系數 10%、42.9%、57.1%和90%的雙極短路故障時，利用所提的保護算法得到的故障距離最大誤差不超過1%。

3.2.2 含過渡電阻分析

前文已研究非金屬性雙極短路故障時的保護算法，根據分析可知，過渡電阻位于故障回路15和故障回路 12之間，在求解線路兩端正極電流比k時，過渡電阻作為兩個故障回路的共有部分從算法上被消掉，因此過渡電阻不影響所提保護方案的定位效果。但是當過渡電阻較大時，故障回路 12和故障回路 15的故障電流很小，導致故障定位的結果誤差偏大。本文設置過渡電阻為5Ω、20Ω和40Ω時的故障定位結果見表2。從表2中可以看出，當過渡電阻分別為 5Ω和 20Ω時，不同線路故障時保護算法定位結果準確可靠，誤差小于 1%。當過渡電阻為 40Ω時，除 Line1故障位置 0.35km時誤差為1.343%外，其余線路誤差均小于1%，定位結果準確可靠。

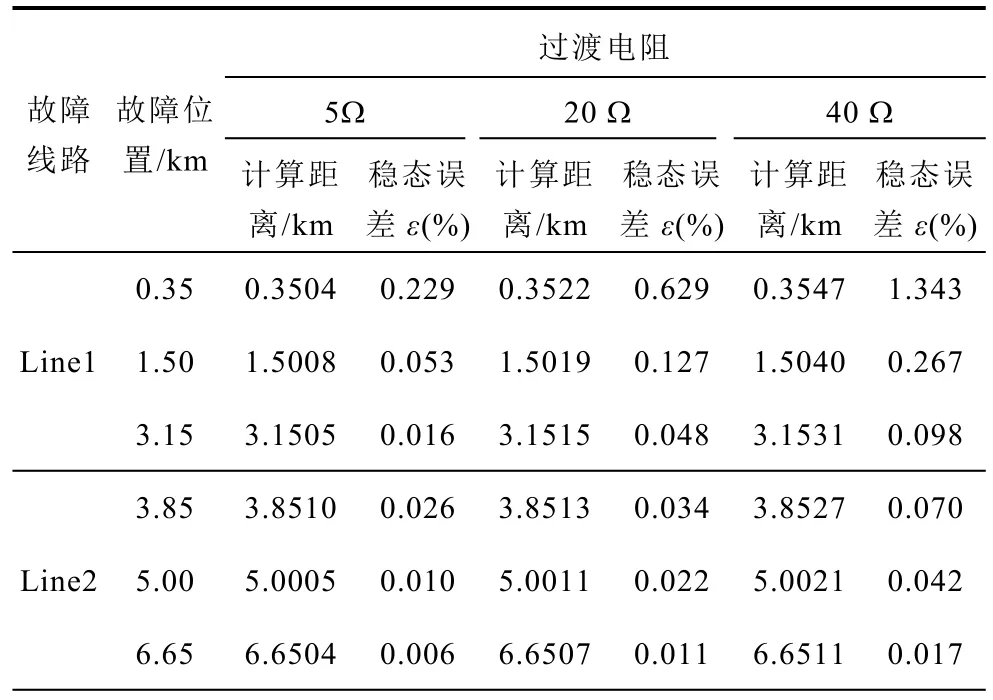
表2 不同位置非金屬性故障定位結果Tab.2 Non-metallic fault location results at different fault positions

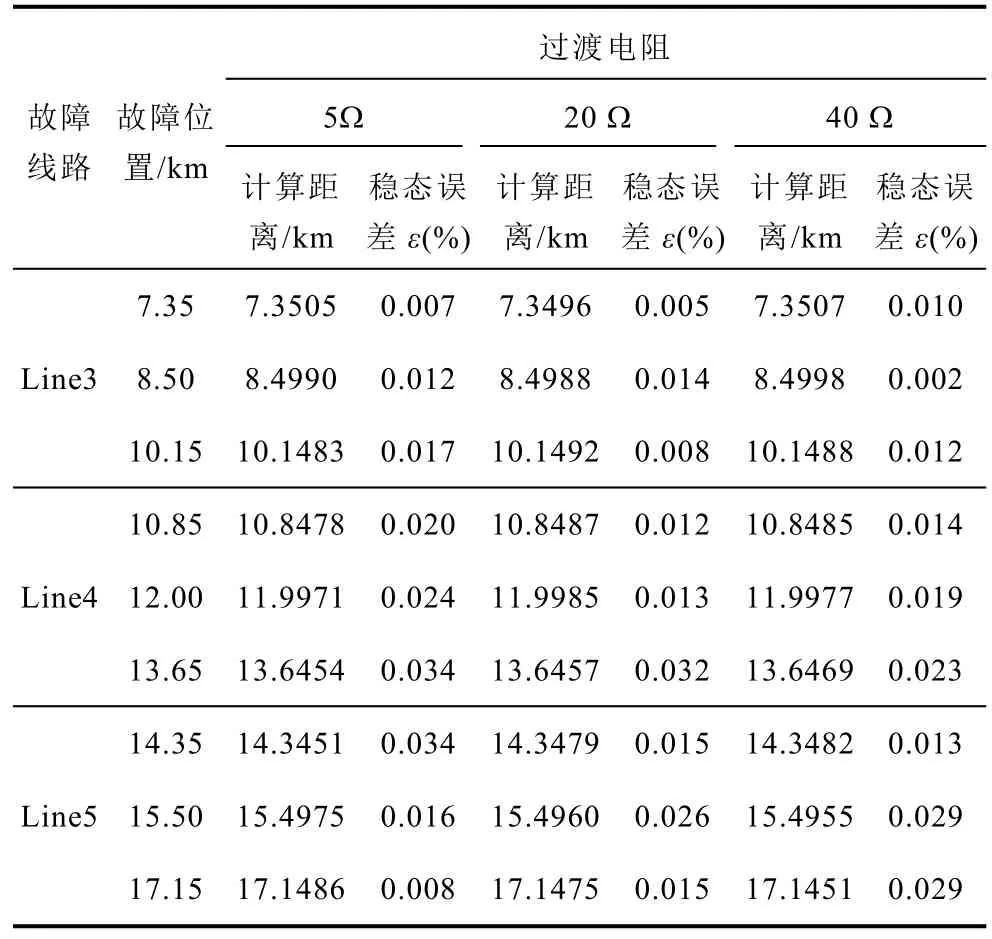
（續）

3.2.3 含分布式電容分析

線路分布式電容對故障電流的影響很大，本文采用分布參數模型分析線路分布式電容對所提保護算法的影響，仿真結果如圖11所示。

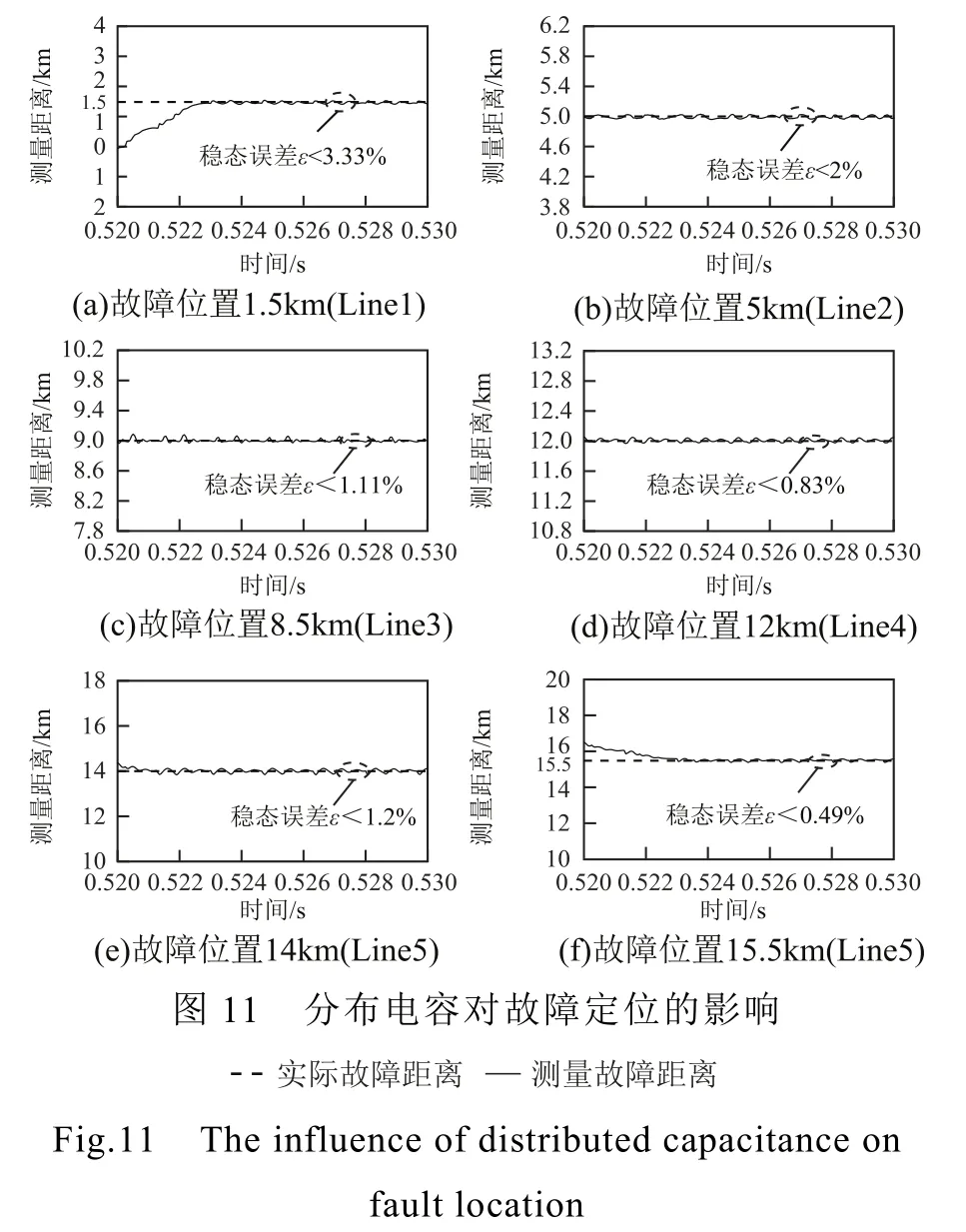
線路分布式電容的故障電流特性會導致 LCC注入的穩態故障電流波動。從圖11可以看出，不同線路故障時，故障定位結果均在實際故障距離點上下波動，穩態誤差小于5%，所提保護算法能夠準確定位故障位置。

3.2.4 含噪聲分析

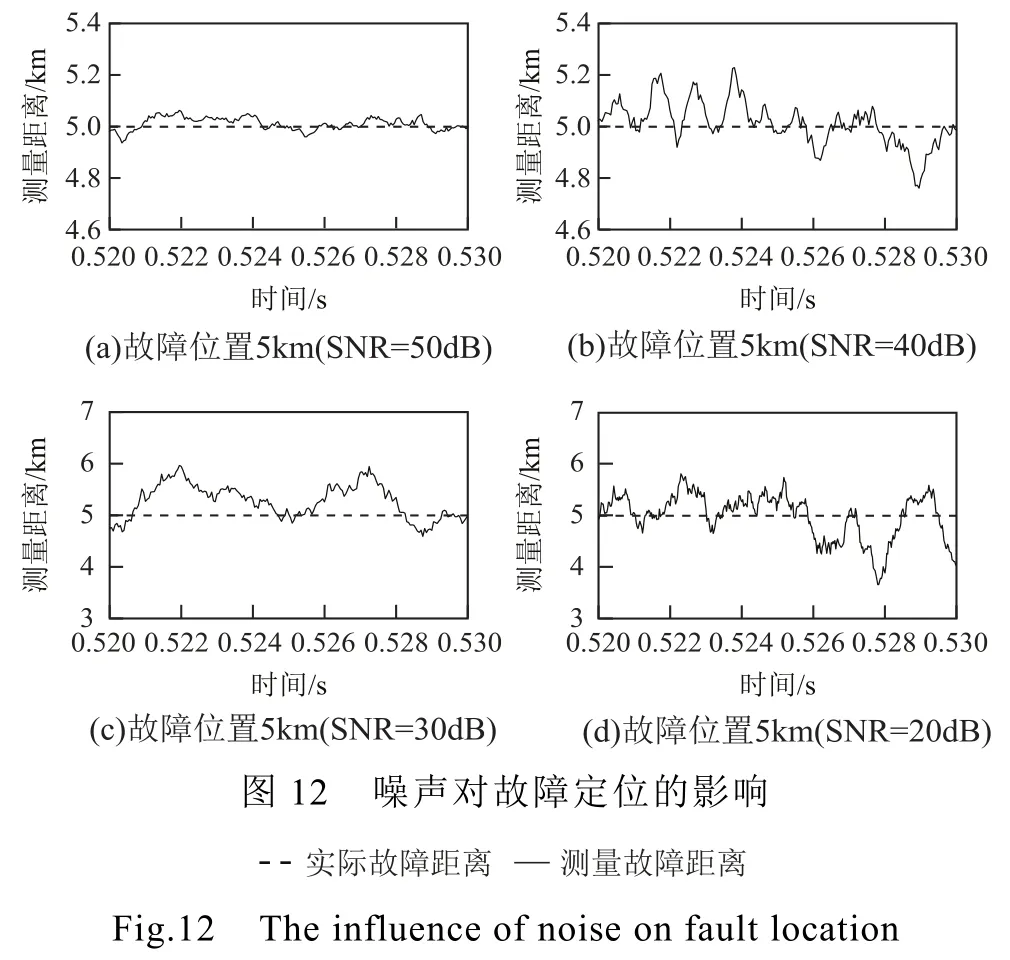
實際工程中的采樣數據往往受到電磁干擾和量測誤差的影響，通常在采樣數據中疊加高斯白噪聲來模擬這些影響[32]。本文分別設置信噪比（Signal to Noise Ratio, SNR）為50dB、40dB、30dB和20dB，以 Line2故障位置系數 42.9%為例，通過仿真分析不同信噪比對所提保護算法的影響。仿真結果如圖12所示。噪聲主要影響 LCC注入的穩態故障電流波動，由于噪聲能量相對穩態的故障電流較低，因此一定程度的噪聲對故障定位結果的影響較小。從圖12可以看出，當SNR=50dB和40dB時，噪聲造成定位結果波動的影響較小，故障定位結果誤差小于5%，所提保護算法定位結果可靠；當SNR=30dB和 20dB時，噪聲對保護算法定位結果的影響顯著增加，定位誤差較大，定位結果不可靠。

4 結論

基于 CDSM-MMC和 DAB直流變壓器閉鎖后LCC提供穩態故障電流的特點，本文提出一種基于LCC注入的混合直流配電系統雙極短路故障保護原理，并進行了仿真驗證。所提保護原理滿足直流配電系統保護選擇性和可靠性的要求，保護原理簡單，計算量小，受過渡電阻和分布式電容影響小，與傳統保護方案相比，無需數值整定，經濟性好，不需解列環網系統即可實現故障邊界的區分，所提保護方案定位結果精確可靠，有利于故障后快速檢修和供電恢復。然而，本文所研究的保護方案缺乏速動性，未來需要進一步研究縮短暫態過程的方法，實現快速的保護。

附 錄

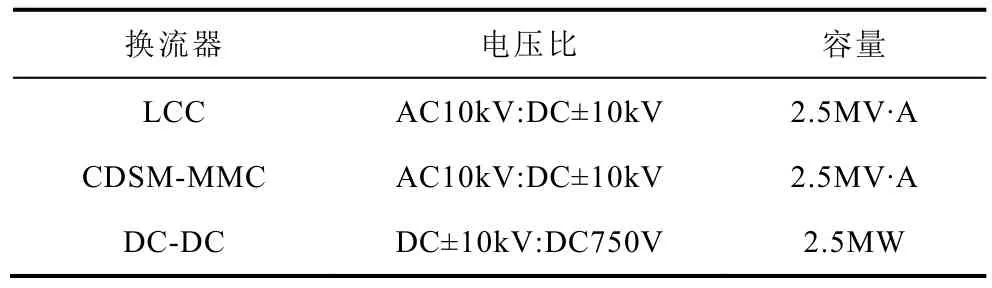
附表1 換流器相關參數App.Tab.1 Related parameters of converters

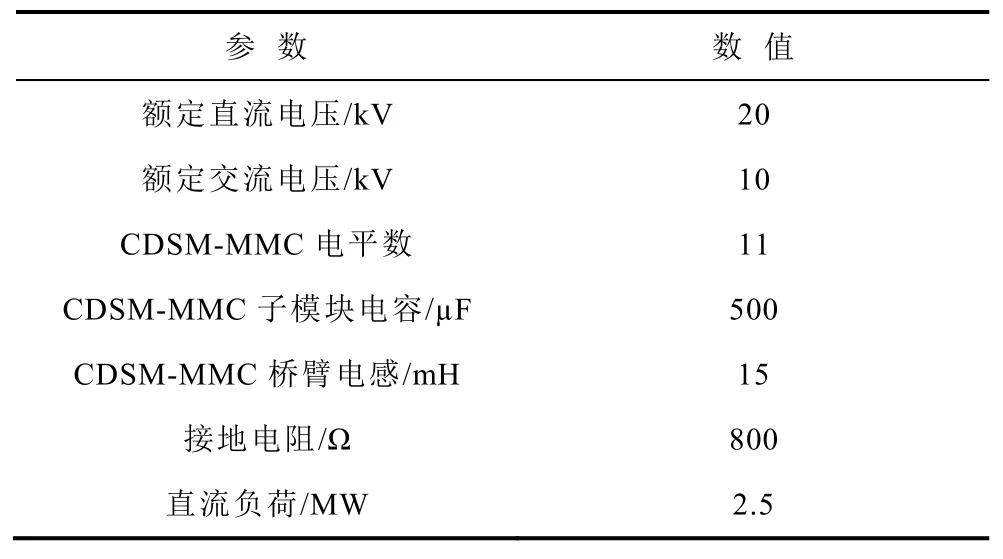
附表2 直流配電網相關參數App.Tab.2 Related parameters of dc distribution network