基于極限學習機與負荷密度指標法的空間負荷預測

邵宇鷹， 彭鵬， 張秋橋， 王冰

(1. 國網上海市電力公司，上海 200122；2. 南京寬塔信息技術有限公司， 江蘇 南京 211100；3. 河海大學能源與電氣學院，江蘇 南京 211100)

0 引言

空間負荷預測這一概念由H. Lee Willis于20世紀80年代初首次提出[1]，不僅要對某一區域的負荷總量進行預測，同時還要預測這一區域負荷增長的位置。空間負荷預測是城市配電網規劃中不可或缺的重要環節，其預測結果的精度對城市配電網規劃的經濟性[2—6]以及可操作性有著重大影響。因此，隨著城市負荷的增長以及智能電網建設需求的增加，空間負荷預測越來越受到重視。

目前，空間負荷預測的方法主要有趨勢法[7]、多元變量法[8]、用地仿真法[9]以及負荷密度指標法[10—12]。用地仿真法是一種自上而下的預測方法，首先將規劃區以網格的形式劃分為面積相同的元胞，然后以土地利用性質為原則對負荷總量預測的結果進行空間位置上的分配[13—14]。負荷密度指標法是一種自下而上的空間負荷預測方法，首先按照負荷類型劃分功能小區，通過預測功能小區的負荷密度，然和結合小區的面積計算出各小區的負荷值，進而得出總量負荷值[15]。這種預測方法適用于未來土地使用較為明確的情況，我國的土地使用方案已經被規劃部門基本制定，因此負荷密度指標法在我國應用較多。

文獻[16]為了解決數據匱乏且難以處理的問題，提出一種基于最小二乘支持向量機的新型配電網空間負荷密度預測算法，引用了灰色關聯度算法來篩選樣本數據，采用混沌粒子群算法優化最小二乘支持向量機參數。文獻[17—18]提出一種考慮了分布式能源以及電動汽車接入的配電網空間負荷預測算法，但是分布式能源與電動汽車是一種復雜的非線性變化，文中只依靠支持向量機算法難以保證預測的精度與準確性問題。

針對上述情況，文中提出基于極限學習機(extreme learning machine,ELM)和負荷密度指標法的空間負荷預測算法，通過劃分小區元胞，對負荷進行詳細劃分，構造精細化的負荷密度指標。基于模糊C均值(fuzzy C-means,FCM)算法進行樣本數據的篩選，利用粒子群優化(particle swarm op-ti-mi-za-tion,PSO)算法優化ELM模型參數，通過實例驗證了所提算法和模型的有效性。

1 ELM算法

人工神經網絡在電力負荷預測中應用較多，且模型的泛化能力以及訓練速度較快，但存在易陷入過擬合以及預測精度不高的問題。針對這些問題，采用ELM算法建立空間負荷預測模型，與傳統神經網絡相比，ELM的泛化性能好，訓練速度更快。在進行空間負荷預測時，主要分為2個步驟：(1) 選取訓練樣本數據代入模型，確定模型的參數；(2) 將要預測的小區特征代入模型，進行預測。

ELM算法是一種單隱含層前饋神經網絡學習算法[19—22]，該算法隨機產生輸入層與隱含層間的連接權重及隱含層神經元的閾值。算法的原理為：假設共有N個訓練樣本(xi，yi)，隱含層有L個神經元，輸入層與隱含層之間的連接權重為W，隱含層與輸出層之間的連接權重為β，激勵函數為g(x)。故網絡的輸出T為：

T=(t1,t2,…,tN)

(1)

(2)

式中：wi=(wi1,wi2,…,win)為隱含層第i個神經元與各個輸入層神經元間的連接權重；βi=(βi1,βi2,…,βim)為隱含層第i個神經元與各個輸出層神經元間的連接權重；bi為隱含層第i個神經元的閾值。

根據式(1)和式(2)可得：

Hβ=TT

(3)

式中：TT為矩陣T的轉置；H為神經網絡的隱含層輸出矩陣。H具體形式為：

(4)

(5)

一般情況下，隱含層神經元要遠遠小于輸入層神經元，故此時H是奇異的，可通過廣義逆矩陣求解奇異矩陣的逆矩陣，即式(4)的解為：

(6)

式中：H+為隱含層輸出矩陣H的Moore-Penrose廣義逆矩陣。

2 FCM算法

為了進一步提高空間負荷預測的精度，在進行仿真之前，需要對訓練樣本進行聚類分析。文中采用了使用較為廣泛的FCM算法對訓練樣本進行聚類分析。FCM算法是利用求解隸屬度來確定每個樣本所屬程度的一種聚類算法，該算法具體求解步驟如下：

(1) 對于N個訓練樣本X={x1,x2,…,xN}，將其劃分為C類，V={v1,v2,…,vc}是C個聚類中心。實際問題中C一般是人為給定的，設定迭代停止條件ε，同時初始化聚類中心V=V0，設置迭代計數器t= 0，模糊權重指數m= 2。

(2) 根據式(7)計算模糊隸屬度矩陣U。

(7)

(8)

式中：uij為樣本xi隸屬于第j類的模糊隸屬度，0≤uij≤1；dkj為樣本xi到第k類聚類中心vk的歐式距離；dij為樣本xi到第j類聚類中心vj的歐式距離，即：

(9)

按下式迭代聚類中心矩陣vj,t+1：

(10)

若‖Vt-Vt+1‖<ε，則停止，輸出U和聚類中心矩陣V；否則令h=h+1，轉至步驟(2)。

個體則是根據隸屬度矩陣每列最大元素位置判斷個體所屬類別，給定輸入樣本，計算其與每一類聚類中心的歐式距離，取最小歐式距離的那一類數據作為回歸模型的訓練樣本，從而極大地提高空間負荷預測精度。

3 基于PSO-ELM的建模

文中采用ELM建立空間負荷預測模型，利用PSO模型的參數提高負荷預測的精度。PSO的原理如下：

PSO算法中每個粒子就是d搜索空間中的一個潛在解，記為Xi=(xi1,xi2,…,xid)。將Xi代入目標函數計算其適應度值，則粒子的“好壞”可用適應度值來評判。第i個粒子的速度則是用一個d維向量表示，記為Vi=(vi1,vi2,…,vid)。在迭代的過程中，第i個粒子搜索到的最佳位置記為Pid=(pi1,pi2,…,pid)，所有粒子搜索到的最佳位置記為Pgd=(pg1,pg2,…,pgd)。粒子根據下式更新速度和位置：

(11)

式中：i=1,2,…,m；k為迭代次數；ω為慣性權重因子；非負常數c1，c2為學習因子；r1，r2為(0,1)間的隨機數。

考慮到粒子在搜索的過程中是非線性變化的，因此采用非線性凹函數遞減慣性權重方式會獲得更好的效果。

(12)

式中：Tmax為最大迭代次數；ωmax，ωmin分別為慣性權重的最大、最小值，通常ωmax取0.9，ωmin取0.4。

由上文對ELM的介紹可知，輸入層神經元個數、隱含層神經元個數以及輸出層神經元個數預先設定，模型未知的參數變量是輸入層與隱含層之間的連接權重W和隱含層神經元閾值b，激勵函數采用Sigmoid函數，目標函數是使式(5)最小。

因此，PSO優化的過程，就是找到使得目標函數最小的ELM最優的輸入層與隱含層之間的連接權重W和隱含層神經元閾值b的過程。通過粒子群的不斷迭代，將模型的目標函數作為粒子群的評價指標，最終滿足精度要求后輸出模型的最優參數。

4 空間負荷預測步驟

采用負荷密度指標法進行空間負荷預測最重要的步驟是建立精細化的負荷密度指標體系，利用FCM算法對樣本數據聚類分析；然后采用文中所提的PSO-ELM模型預測，將負荷密度作為模型的輸出，結合小區的面積求出小區的負荷大小。空間負荷預測的具體步驟如下。

(1) 構建精細化的負荷密度指標體系。文中將電力負荷根據用電性質分為以下10類：工業負荷，居民住宅負荷，行政辦公負荷，商業負荷，文化娛樂負荷，研發負荷，教育、醫療、體育等公共設施負荷，市政設施負荷，倉儲物流負荷，綠化、廣場及道路負荷。分析搜集到的數據可知，每一類負荷從最大值到最小值的跨度較大，有必要對每一類負荷再進行細分，見圖1。等級1到等級T表示將每一類負荷再細分為T類，通過上文提到的FCM算法實現。

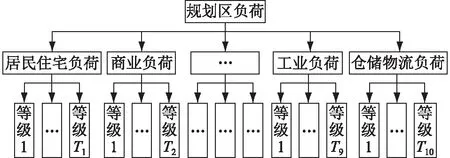
圖1 負荷密度指標體系Fig.1 Load density index system

(2) 確定訓練樣本。利用FCM聚類算法，將每類負荷再細分為幾個類型。以居民住宅為例，將這一類負荷分為再5種類型，求出每一類的聚類中心矩陣。對于給定的待預測地的特性指標，求出與5個聚類中心的歐式距離，取距離最小的那一類樣本作為訓練樣本。

(3) 建立回歸模型。文中采用的回歸模型是基于PSO的ELM算法，將選好的訓練樣本代入模型，影響因素作為模型的輸入，負荷密度作為模型的輸出。訓練好模型后，代入待預測地的特性指標，即可得出待預測地未來年的負荷密度。

(4) 進行空間負荷預測。將求出的各類負荷密度ρi乘以小區的面積Si即可得每個小區的負荷值Wi，將小區負荷相加并進行修正即可得到規劃區的總量負荷。

(13)

式中：pi為小區的同時系數；N為小區個數；W為預測的空間負荷值。

根據以上4個步驟，基于ELM和負荷密度指標法的空間負荷預測流程如圖2所示。

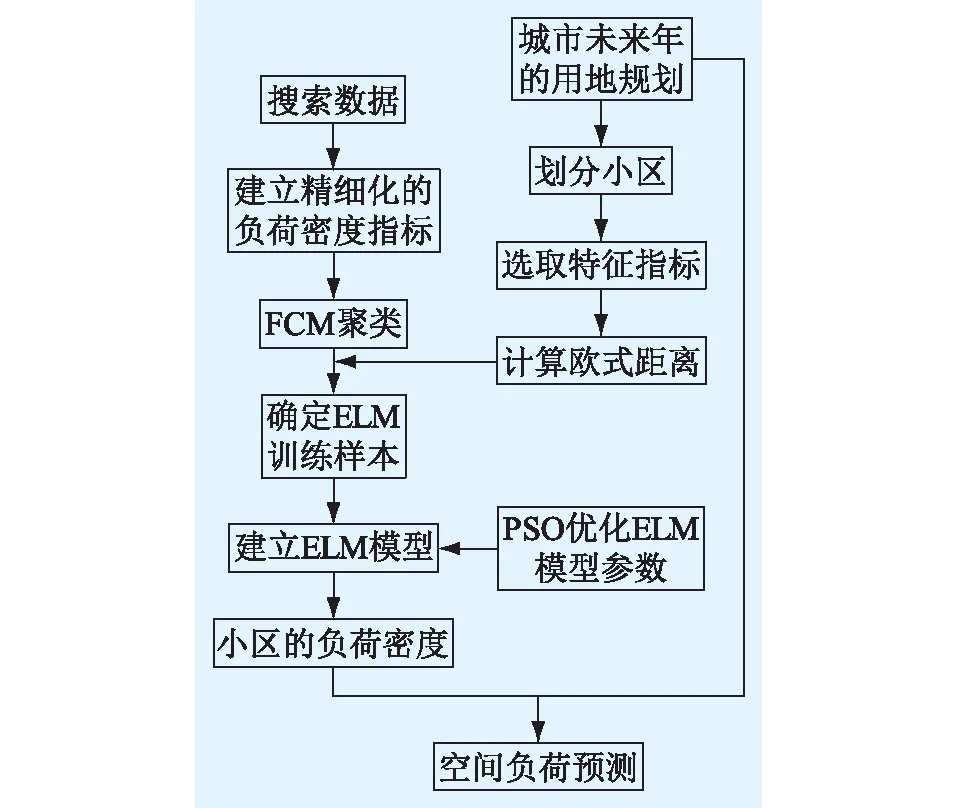
圖2 空間負荷預測總流程Fig.2 General flow chart of space load prediction

5 算例分析

以居民住宅負荷為例，搜集上海市某規劃地小區居民負荷數據樣本，參考負荷密度指標體系可知，影響居民住宅負荷的主要因素為：人口密度A1，人均收入A2，人均用電量A3，煤電價格比增長率A4及回歸模型的輸出負荷密度C。搜集到的128個居民住宅樣本數據如表1所示。

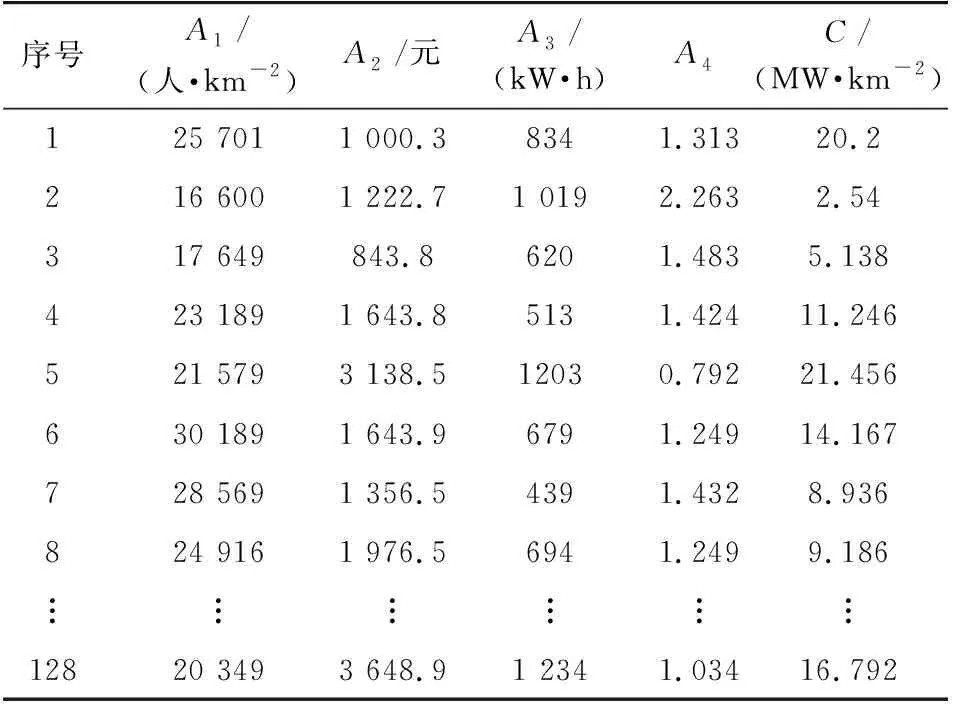
表1 樣本數據Table 1 Sample data

考慮到居民住宅負荷密度大小跨度較大，因此將其再細分為5類，使用FCM算法將其聚類，每一類的聚類中心以及樣本數如表2所示。

表2 各類負荷的聚類中心矩陣和樣本數目Table 2 Cluster center matrix and sample number of each load

已知預測小區影響因素的數值為：A1=26 431，A2=1 576.3，A3=751，A4=1.379，對數據進行歸一化處理，計算該樣本與上述5類樣本距離中心矩陣的歐式距離，采用標量值表示，記為d={0.048 7,0.657 3,0.313 2,0.685 4,0.238 6}。計算結果表明，預測小區與第一類負荷的歐式距離最小，故選取第一類負荷的28個樣本數據作為訓練樣本訓練極限學習機回歸模型。文中使用Matlab建立ELM模型，利用PSO算法來對ELM的參數進行優化。

采用絕對誤差EAE和相對誤差ERE作為評價指標：

EAE=|C-C′|

(14)

(15)

為了驗證文中所提算法的有效性，分別對未采用FCM算法、未采用PSO算法與文中所提算法進行比較，預測結果如表3所示。

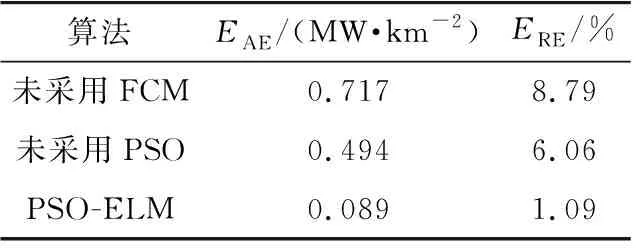
表3 3種算法的預測結果比較Table 3 Comparison of prediction results of three algorithms

由表3可知，PSO-ELM算法精度最高，且誤差滿足實際的工程要求。FCM聚類算法只是對數據進行處理，沒有改變模型本身的復雜性。PSO算法優化耗時較短，因此引入PSO算法并不會影響模型的計算速度。

對于上述小區的負荷大小，可通過負荷密度乘以小區面積獲得，對于規劃地的空間負荷總量的預測則需要預測出每個小區的負荷密度大小，然后求取每個小區的負荷大小。表4給出了另外3個小區的特性指標，采用上述的PSO-ELM算法預測負荷密度大小。

表4 預測結果分析Table 4 Analysis of prediction results

按照此方法，求出規劃區內所有的小區負荷密度，即可得到居民區空間負荷分布規律。文中在求取總負荷時，參考統計數據，設置同時系數為0.9，將每個小區負荷疊加修正即可得到總的空間負荷大小。

6 結語

文中所采用的空間負荷預測的算法是基于我國土地開發的實際情況提出的，我國土地的規劃主要由政府決定，土地的使用性質明確，故可采用負荷密度指標法。文中采用的回歸模型是ELM，該算法屬于神經網絡范疇，具有運行速度快、自學習能力強等優點。但是該算法也容易陷入過擬合狀態，因此采用了改進的PSO算法來對其參數進行尋優處理。文中提出的負荷密度指標法意在建立精細化的負荷密度指標體系，采用FCM算法對每一類負荷進行再細化的聚類，為ELM提供訓練樣本，提高預測的精度。仿真試驗證明，該算法具有很強的實用性。

本文得到國網上海市電力公司“基于智能算法的配電網空間負荷聚類及預測研究”(52-0-9-7-0-1-8-0-0-0G)資助，謹此致謝！