含相變壓力振蕩改進算法及其驗證

劉 培 啟，李 想，馮 明 宇，于 洋，胡 大 鵬

( 大連理工大學 化工學院, 遼寧 大連 116024 )

0 引 言

波轉子技術通過氣體自身壓力能來實現能量的傳遞．該技術的核心部件為波轉子，是一種由若干雙開口方形直管，即壓力振蕩管(pressure oscillation tube)組成的轉轂[1]．目前波轉子技術已廣泛應用于增壓和制冷領域[2]，該技術在制冷領域的應用便是壓力振蕩制冷技術．

壓力振蕩制冷技術依靠高壓氣體與低壓氣體間產生的壓力波完成能量的直接交換．低壓氣體經激波壓縮為高溫氣體，而高壓氣體經膨脹波膨脹為低溫氣體．目前，壓力振蕩制冷技術已經廣泛應用在天然氣脫水、低溫風洞等冷凝分離工藝領域．起初，壓力振蕩制冷技術依靠單開口壓力振蕩管實現制冷．然而當進氣含有水蒸氣等可凝組分時，壓力振蕩管內凝結形成的液體無法徹底排出并不斷地積聚在振蕩管的封閉端，最終導致制冷性能下降[3]．Dai等提出用波轉子取代單開口壓力振蕩管應用在壓力振蕩制冷技術中[4]．由于波轉子內壓力振蕩管兩端開口，管內的液滴不會形成堆積而是通過任一管口排出，這樣既提高了壓力振蕩制冷技術的帶液能力，也減小了設備的占地面積[5]．在此基礎上，趙家權對壓力振蕩管內高壓氣體的膨脹功進行回收，進一步提高了壓力振蕩制冷技術的制冷效率[6]．

在壓力振蕩制冷的過程中，如果進氣是含濕天然氣等含有可凝組分的混合氣，壓力振蕩管內會存在包含凝結與蒸發在內的相變行為．而可凝組分的凝結過程會產生壓力波，對壓力振蕩管內原有波系造成干擾[7]．由于壓力振蕩制冷技術依靠壓力波的運動實現制冷且壓力振蕩管與各端口之間的匹配往往依據忽略相變的理想波系進行設計，凝結過程會使得內部實際波系偏離理想波系，從而使得壓力振蕩制冷的效率無法達到最大值．近幾年來，科研工作者開始重視壓力振蕩管內的相變過程．趙家權等忽略蒸發現象，建立了理想氣體凝結數值模型，并模擬了壓力振蕩管內的凝結過程，探究了凝結對于流場的影響[8]．徐思遠搭建了壓力振蕩管相變可視化實驗平臺，并通過高速攝影捕捉到管內的凝結行為[9]．吳柯含將蒸發模型與凝結模型相結合，對壓力振蕩管內理想氣體的凝結與蒸發過程進行了數值分析[10]．然而作為可凝組分的水是極性物質，水分子相互締合形成氫鍵，使得其實際熱力學性質與并沒有考慮到氫鍵作用的理想氣體偏差較大[11]．因此，利用理想氣體狀態方程無法準確地對壓力振蕩管內水的相變行為進行數值計算．

本文利用CPA氣體狀態方程對壓力振蕩管內凝結蒸發數值模型進行改進，并通過實驗對改進后的數值模型進行驗證．在此基礎上，本文分別利用改進后的數值模型與理想氣體模型對濕空氣壓力振蕩制冷過程進行數值計算，并對計算結果進行對比總結．

1 壓力振蕩制冷技術

壓力振蕩制冷技術的工作過程可通過將波轉子與各端口展開得到的二維波系圖進行描述，如圖1所示．當壓力振蕩管與高壓入口接通時，由于二者之間存在壓差，激波S1會在二者交界處形成并向管內運動，壓縮管內氣體．同時相對地，在高壓入口與管內氣體之間也會形成一系列膨脹波使得高壓進氣溫度和壓力降低．當向上移動的壓力振蕩管與高溫出口接通時，被激波加熱的氣體通過高溫出口排出，同時激波到達壓力振蕩管的右端并反射形成一系列左向移動的膨脹波E1進一步膨脹管內氣體．隨后，在壓力振蕩管與高壓入口錯開時，由于管內氣體的慣性，振蕩管的左側會形成一系列右向膨脹波E2再一次膨脹管內氣體．管內氣體經膨脹波多次膨脹后溫度和壓力下降至某一較低值．從高溫出口流出的氣體經過換熱至室溫后從中壓入口流回壓力振蕩管，管內低溫低壓氣體會在壓力振蕩管兩側壓差的推動下由低溫出口排出．一個周期的制冷過程結束．在整個制冷過程中高壓進氣與管內原有氣體之間會形成較為明顯且隨著時間運動的交界面．兩股氣體之間存在通過交界面換熱的現象，但是不存在較為明顯的混合現象．

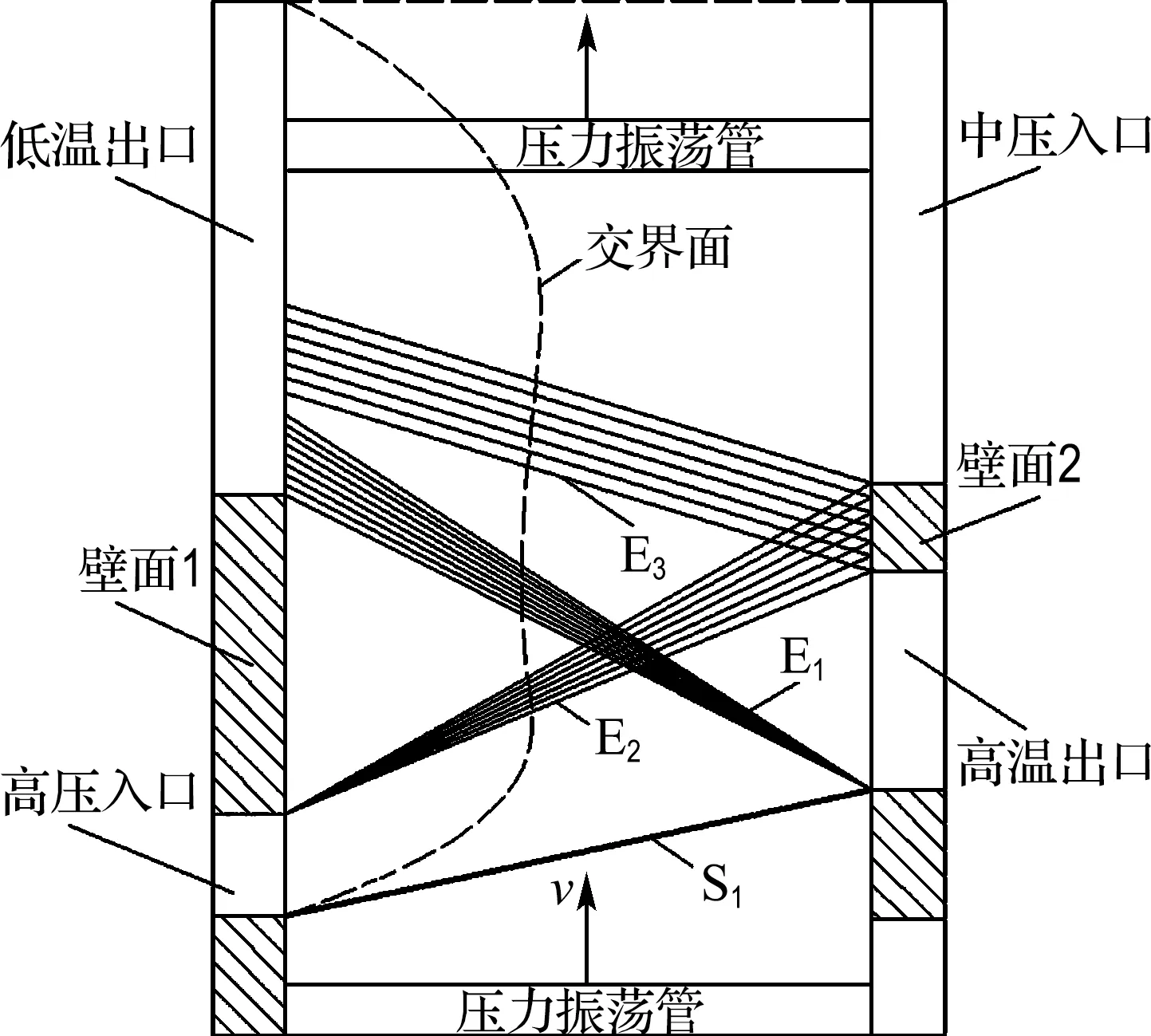
圖1 壓力振蕩制冷波圖

制冷效率，即等熵效率η，是用來衡量壓力振蕩制冷技術制冷性能的重要參數，其表達式為

(1)

式中：T1為高壓進氣溫度，K；T2為低溫排氣溫度，K；p1為高壓入口壓力，kPa；p2為低溫出口壓力，kPa；γ為絕熱系數．

當壓力振蕩制冷技術應用在天然氣脫水等冷凝分離技術中時，液化率也是衡量其工作性能的重要參數．在本文中，液化率是低溫出口液態水的質量流量與高壓進氣中水蒸氣的質量流量的比值．液化率利用進出口水蒸氣質量分數可表達為

(2)

式中：α為液化率，w1為高壓入口的水蒸氣質量分數，w2為低溫出口的水蒸氣質量分數．

2 數值模擬及流場分析

含濕壓力振蕩制冷實驗平臺以及實驗流程如圖2、3所示．經壓縮機排出的高壓空氣首先流向兩條管路．在一條管路中，高壓空氣在經過霧化器與過濾器后獲得飽和水蒸氣，而在另一條管路中，空氣經吸收式干燥機后成為干空氣．通過控制兩條管路的氣體流量并將二者混合，就可以控制壓力振蕩管進氣的相對濕度．在壓力振蕩管進氣端安裝濕度儀可以對其濕度進行監測．壓力振蕩管的尺寸參數如表1所示．

圖2 實驗平臺

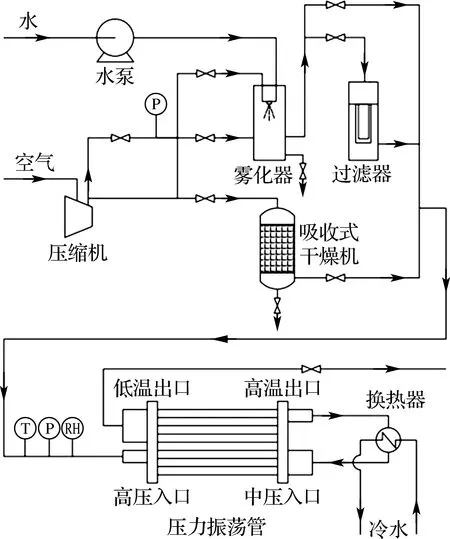
圖3 實驗流程

表1 壓力振蕩管結構參數

3 數值模型

3.1 凝結蒸發模型

在建立凝結蒸發模型前，本文作出如下假設：液滴與氣體之間無滑移，液滴體積為零，液滴之間無相互作用，液滴內部溫度分布均勻，流場中沒有離子、灰塵等外界顆粒．

凝結過程分為成核與液滴生長兩部分．由于流場已被假定沒有外界顆粒，壓力振蕩管內的成核過程為均相成核，即蒸汽分子自身聚集形成凝結核．本文采用由經典成核模型發展而來，經由Feder修正后的Frenkel均相成核率公式[12]：

(3)

式中：J為成核率，1/(kg·s)；qc為凝結系數；ρv為可凝氣體密度，kg/m3；ρl為液滴密度，kg/m3；Mm為可凝組分的摩爾質量，kg/mol；φ為Feder絕熱修正系數；r*為凝結臨界半徑，m；σ為液滴表面張力，N/m；k為玻爾茲曼常數，1.38×10-23J/K．

對于液滴生長模型，采用經實驗驗證有效的Hertz-Knudsen方程[13]：

(4)

式中：r為液滴半徑，m；t為時間，s；p為壓力，kPa；T為溫度，K；R為氣體常數，8.314 J/(mol·K)．

對于滴液蒸發模型，經實驗驗證，采用逆向描述Hertz-Knudsen方程的方法可有效地描述液滴的蒸發行為[14]，因此本文采用同種方式對蒸發行為進行描述．

3.2 數值模型改進

為解決理想氣體相變模型計算準確性不足的問題，本文采用可以準確描述極性物質性質的CPA氣體狀態方程對數值模型進行改進．CPA氣體狀態方程由SRK方程作為物理項和Wertheim 理論提出的締合項組成[15]，可以較為準確地描述極性氣體的逸度、比熱容等參數．

(5)

式中：V為摩爾體積，L/mol；a為SRK方程物理項能量參數，kPa·L2/mol2；b為SRK方程物理項的體積參數，L/mol；g為徑向分布函數；xi為組分i的摩爾分數；xAi為分子i上沒有與其他端位締合的A端的摩爾分數．

如果計算介質為混合氣，需要采用混合規則對混合物的物理參數進行定義．本文采用經典的范德華混合規則[16]．

(1)密度計算

在理想氣體相變模型中，氣體密度通過理想氣體狀態方程求得，液體密度由于可壓縮性較差，則默認不變．在本文的改進模型中，氣體與液體的密度通過CPA氣體狀態方程在壓力p、溫度T下求得．

(2)相平衡計算

在相變過程中需要對可凝組分的氣液相平衡進行計算．理想氣體相變模型并沒有考慮到可凝氣的相平衡．由于處于相平衡狀態的組分在各相中的逸度相等，在改進模型中，逸度將作為判斷相平衡的基本參數．CPA氣體狀態方程中各組分的逸度系數可由剩余亥姆霍茲能求出[17]，即

(6)

式中：Ar為剩余亥姆霍茲能，J；φi為組分i的逸度系數；ni為組分i的物質的量，mol．

CPA氣體狀態方程的剩余亥姆霍茲能由SRK物理項和締合項兩部分組成[18]，即

(7)

(8)

(9)

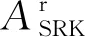
(3)其他熱力學參數計算

由于數值模擬中涉及能量的傳遞，需要對介質的熱力學參數進行改進．這些熱力學參數包括定壓比熱容cp、定容比熱容cV、絕熱系數γ以及聲速c．

CPA氣體的cp可通過下式進行計算：

cp=(?H/?T)p

(10)

(11)

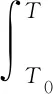
(12)

計算得出cp后，cV可通過下式進行計算：

(13)

據此便可求出聲速c與絕熱系數γ[19-20]：

(14)

γ=cp/cV

(15)

3.3 幾何模型及求解器設置

壓力振蕩管的三維模型可以準確地模擬其內部的流場，存在的不足就是對電腦性能要求較高且計算時間較長．由于壓力振蕩管的長徑比大于10，且其轉速較低，離心力對流場的影響可以被忽略．除此之外，在過去的研究中將壓力振蕩管沿周向展開得到的二維模型已經被證實可以準確地描述內部流場[21]．因此，本文采用與實驗設備尺寸相同的二維模型進行數值計算．計算模型網格劃分如圖4所示．壓力振蕩管與各個端口之間采用滑移網格，振蕩管的上下邊界設為周期性邊界．高壓入口設置為壓力入口，高溫、低溫出口設置為壓力出口．中壓入口設置為質量流量入口且通過自定義函數(UDF)將其質量流量設置為與高溫出口相等．

圖4 幾何模型與網格劃分

氣波制冷機的內部流場為可壓縮非定常流場，該流場遵循動量守恒定律、質量守恒定律和能量守恒定律．控制方程為

(16)

(17)

式中：μ為黏度系數，Pa·s；λ為流動介質的傳熱系數，W/(m·K)；Su和Sv均為源項；ST為黏性耗散項：

(18)

(19)

(20)

湍流模型采用Realizablek-ε方程．模擬介質采用濕空氣．采用AUSM格式進行離散，其廣泛用于不同音速下氣體流場的計算．求解格式選用基于密度求解，時間步長為1×10-6s，計算過程中，保證各時間步下連續性、速度、能量、湍流模型參數、液滴數量、氣相質量、液相質量各參數的最終殘差值均小于1×10-3．該數值計算需要對計算流域賦予初值，初值不會影響計算結果，為保證計算的收斂性，對全場流域賦予溫度298 K、總壓0.1 MPa的初值．

3.4 理論模型驗證

膨脹激波管的內部流動與壓力振蕩管相似，因此本文采用埃因霍芬大學進行的水蒸氣-氦氣混合氣在脈沖膨脹激波管內相變的實驗數據[22]分別對改進前后的凝結蒸發數值模型進行驗證．如圖5所示為脈沖膨脹激波管高壓區末端處液滴半徑變化的實驗值與數值模擬結果．

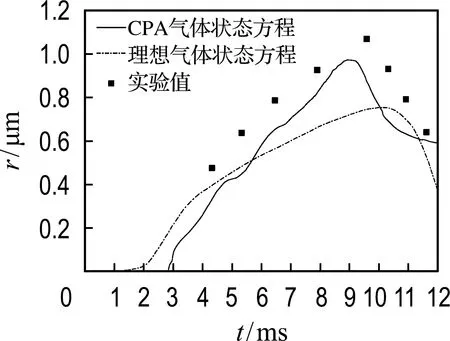
圖5 膨脹激波管內液滴半徑分布

可見，從液滴半徑的大小與變化趨勢來看，采用CPA氣體狀態方程改進過的凝結蒸發模型更能準確描述水蒸氣的相變行為．

4 結果與討論

實驗的操作條件：高壓進氣溫度為298 K，總壓設置在0.2～0.4 MPa，進氣中水蒸氣的相對濕度固定不變為100%．低溫出口壓力設為0.1 MPa，中壓回氣溫度設置為298 K．對于數值模擬，在與實驗相同的操作條件下，分別對CPA氣體與理想氣體在壓力振蕩管內的制冷過程進行數值模擬并將模擬結果與實驗結果進行對比．

在進氣壓力為0.2 MPa時的溫度云圖如圖6所示．可見在壓力振蕩管的左側低溫區，CPA氣體的溫度高于理想氣體．提取數值模擬與實驗結果并計算制冷效率，可得到制冷效率隨進氣壓力的變化曲線如圖7所示．從曲線可知，雖然CPA氣體與理想氣體的制冷效率變化趨勢相同，都是隨著進氣壓力的增加而逐漸上升且上升趨勢逐漸平緩，但是CPA氣體的壓力振蕩制冷效率與實驗值最為接近，二者最大差值僅為0.5%，最小差值為0.35%．且隨著進氣壓力的增加，CPA氣體與理想氣體制冷效率差值Δη也逐漸增大．

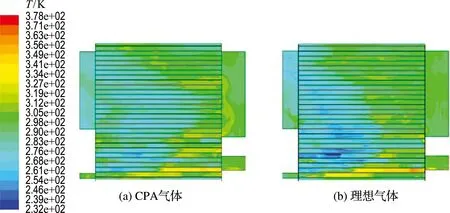
圖6 高壓進氣0.2 MPa下溫度云圖

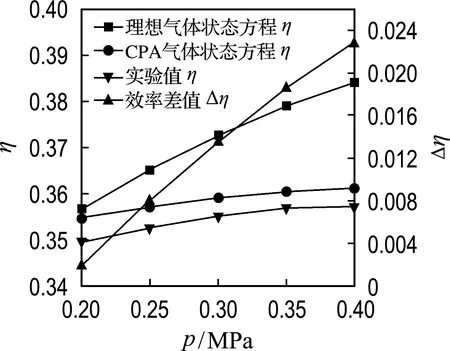
圖7 制冷效率與高壓進氣壓力關系

造成CPA氣體與理想氣體狀態方程數值模擬結果存在差距的主要原因是壓力振蕩管內實際波系與理想波系存在偏差[23]．在壓力振蕩管中，激波是由多數壓縮波疊加形成并且管中壓縮波與膨脹波的移動速度為聲速．提取計算結果中的聲速云圖如圖8所示．可見在標示出的激波形成區中，CPA氣體中的聲速與理想氣體不同，這導致了激波的形成與運動存在偏差，進一步導致了后續壓力波系的偏差．而壓力振蕩制冷技術依靠壓力波的運動實現制冷，并且目前壓力振蕩管與各端口的匹配基于理想氣體內的波系運動進行設計．因此CPA氣體中壓力波無法與各端口很好地匹配，導致了制冷效率的下降．除此之外，相較于CPA氣體，壓力波在理想氣體中能量傳遞效率較高，因此經CPA氣體狀態方程對氣體的熱力學參數計算進行改進后，壓力波在壓力振蕩管內的能量傳遞效率有所降低，這也是導致CPA氣體制冷效率較理想氣體低的原因之一．二者制冷效率的差別隨著進氣壓力的升高而增加，這是因為CPA氣體的壓力越高，其狀態偏離理想氣體狀態的程度越大．

分別利用改進前后的數值模型對水蒸氣在壓力振蕩管內的液化率進行計算．圖9為進氣壓力0.2 MPa下水蒸氣質量分數云圖．可見在CPA氣體中水蒸氣的質量分數較高，說明其凝結成液態水的量較少．提取進出口水蒸氣的質量分數計算液化率可得到水蒸氣液化率隨著進氣壓力變化的曲線以及CPA氣體與理想氣體液化率差值Δα的變化曲線，如圖10所示．可見CPA氣體與理想氣體在壓力振蕩管中液化率的變化趨勢相同，即隨著進氣壓力的提升液化率先上升后下降并在進氣壓力為0.30 MPa時達到最大值．這一變化趨勢是由壓力振蕩管內波系與各端口之間的匹配引起的．對比CPA氣體與理想氣體中水蒸氣的液化率，發現CPA氣體中水蒸氣的液化率低于理想氣體，且兩者之間的差值也隨著進氣壓力的增加而逐漸增加．這是因為水蒸氣的凝結主要取決于其分壓與溫度．由于水蒸氣在凝結過程中相對濕度保持為100%，其分壓僅取決于溫度．因此水蒸氣的溫度決定了其凝結過程．由于CPA氣體的制冷效率低于理想氣體，壓力振蕩管內CPA氣體的溫度高于理想氣體，這導致了CPA氣體中水蒸氣的凝結受到了抑制，液態水的質量減少．隨著進氣壓力的增加，CPA氣體與理想氣體之間制冷效率差距的增加也導致了液化率差距的增加．

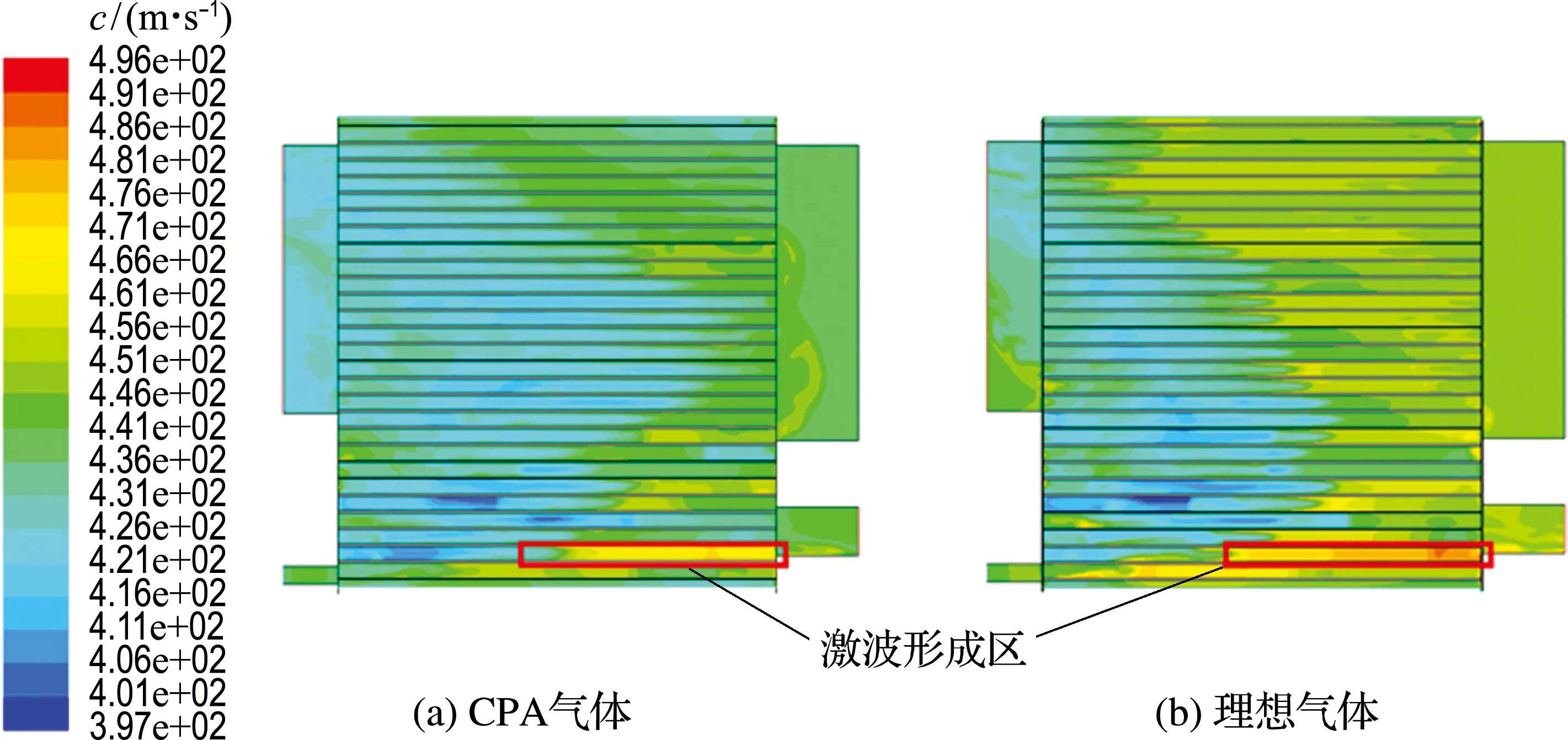
圖8 高壓進氣0.2 MPa下聲速云圖

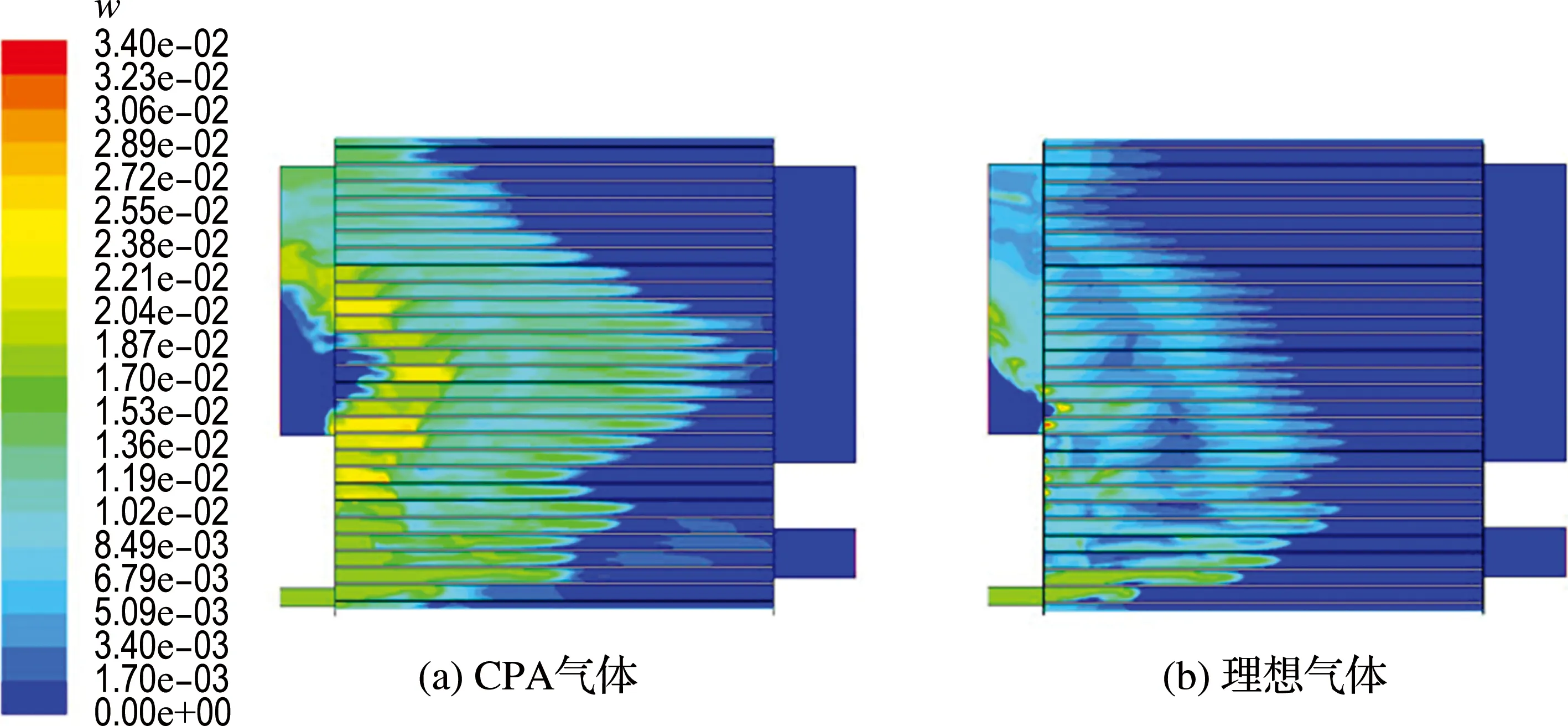
圖9 高壓進氣0.2 MPa下水蒸氣質量分數云圖

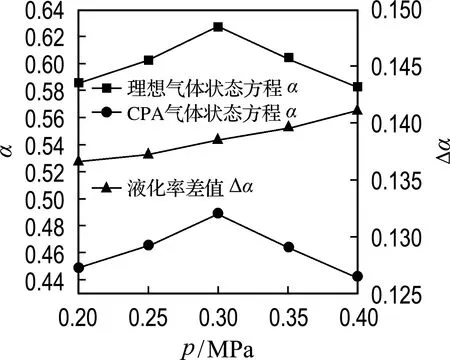
圖10 水蒸氣液化率與高壓進氣壓力的關系

5 結 論

(1)通過與實驗數值對比發現，CPA氣體狀態方程改進后的凝結蒸發模型相較于理想氣體模型可以更準確地描述含濕氣體凝結蒸發行為，是一種有效的含相變壓力振蕩數值計算方法，為含濕天然氣壓力振蕩制冷提供了理論基礎．

(2)隨著高壓進氣壓力從0.2 MPa增加至0.4 MPa，CPA改進模型和理想氣體模型得到的制冷效率的差距逐漸增大，其中CPA改進模型數值偏低，更接近實驗結果，計算得到的制冷效率變化趨勢也更符合實際．

(3)隨著高壓進氣壓力從0.2 MPa增加至0.4 MPa，CPA改進模型獲得的壓力振蕩管內含濕空氣液化率的變化規律與理想混合氣相似．在數值上，CPA改進模型得到的含濕氣體液化率低于理想氣體，且兩者差距隨著高壓進氣壓力的升高而增加．該結論可為含濕天然氣制冷后的氣液分離過程提供設計依據．