波能裝置浮子選型及水動(dòng)力性能分析

孫科， 解光慈， 周斌珍

(1.哈爾濱工程大學(xué) 船舶工程學(xué)院，黑龍江 哈爾濱 150001; 2.中山大學(xué) 海洋工程與技術(shù)學(xué)院，廣東 珠海 519082； 3.華南理工大學(xué) 土木與交通學(xué)院,廣東 廣州 510000)

波浪能作為一種新型的海洋可再生能源，具有儲(chǔ)量大、分布廣的特點(diǎn)[1]。而波浪能裝置的形式也是多種多樣的，有點(diǎn)吸收式、振蕩水柱式以及越浪式等[2]。如今，越來(lái)越多的國(guó)家研究波浪能利用技術(shù)，主要研究方面包括波能轉(zhuǎn)換水動(dòng)力研究、PTO系統(tǒng)研究以及波能浮子與平臺(tái)的耦合運(yùn)動(dòng)等[3]。其中浮子的形狀很大程度上決定了其水動(dòng)力性能。

對(duì)于波浪能浮子的研究方法有很多種，最常用的方法有基于勢(shì)流理論的邊界元法和基于N-S方程的計(jì)算流體動(dòng)力學(xué)(CFD)方法。

在波浪的研究中，勢(shì)流理論一直占據(jù)主導(dǎo)地位。2013年，周斌珍等[4]利用高階邊界元研究波浪與結(jié)構(gòu)物的非線性相互作用；張萬(wàn)超等[5]在2016年基于勢(shì)流理論對(duì)軸對(duì)稱浮子進(jìn)行水動(dòng)力特性研究。Zhang等[6]基于勢(shì)流理論和高階邊界元法，建立了只考慮雙浮體垂蕩運(yùn)動(dòng)的數(shù)值模型，研究其水動(dòng)力性能和時(shí)域響應(yīng)。常見的基于勢(shì)流理論的軟件有WAMIT、AQWA以及SEASUM。然而由于其無(wú)旋無(wú)粘的前提假設(shè)，使得這一理論只適用于處理一些大結(jié)構(gòu)物或者粘性影響并不顯著的流動(dòng)問題。

而隨著計(jì)算機(jī)性能的不斷發(fā)展，計(jì)算流體動(dòng)力學(xué)隨之誕生，通過對(duì)整個(gè)計(jì)算域離散化，利用有限差分法、有限體積法等方法計(jì)算。CFD方法能夠考慮物體的粘性，并且可對(duì)復(fù)雜幾何形狀的物體計(jì)算，因此成為許多研究者們的選擇。國(guó)威[7]在2016年基于CFD方法模擬浮子的線性波上浪、非線性波抨擊及自由面形變的時(shí)域非線性問題；Bhinde等[8]在2009年基于CFD方法研究一種點(diǎn)吸收式的波能浮子的水動(dòng)力特性以及幾何形狀的優(yōu)化并與實(shí)驗(yàn)作對(duì)比；Ransley等[9]在2017年基于CFD方法研究波能浮子在極端海況的生存能力；Wang[10]通過綜述近年來(lái)用CFD數(shù)值方法解決的船舶與海洋工程中的復(fù)雜問題，討論了立管渦激振動(dòng)、浮式風(fēng)力機(jī)以及高速船在波浪中的運(yùn)動(dòng)等方面的引用，來(lái)描述計(jì)算流體力學(xué)技術(shù)的發(fā)展。常見的CFD商用軟件有CFX、STARCCM+以及FLUENT等。然而CFD方法對(duì)于網(wǎng)格的數(shù)量及質(zhì)量要求很高，計(jì)算時(shí)間長(zhǎng)，對(duì)計(jì)算機(jī)性能要求高，不適合大范圍的算例計(jì)算。

對(duì)于波浪能裝換裝置來(lái)說(shuō)，浮子選型對(duì)能量轉(zhuǎn)換效率有很大影響，國(guó)內(nèi)外學(xué)者針對(duì)這一方面做出了大量研究。張亮等[11]基于CFD方法研究圓柱和圓臺(tái)浮子的阻尼系數(shù)、浮子質(zhì)量對(duì)裝置性能的影響規(guī)律。Zhang等[12]通過邊界離散化(BDM)的半解析方法分析復(fù)雜軸對(duì)稱浮體，分析對(duì)比了圓柱、錐形以及半球形浮子的水動(dòng)力性能。然而以上研究對(duì)于浮子形狀分類較少以及沒有結(jié)合分析流場(chǎng)機(jī)理。而關(guān)于粘性修正方面，同樣也有許多學(xué)者在研究，Liu等[13]在對(duì)浮體進(jìn)行分析時(shí)，通過在自由表面邊界中引入耗散項(xiàng)來(lái)考慮粘性效應(yīng)。田博等[14]基于RANS所求得的水動(dòng)力系數(shù)與勢(shì)流理論結(jié)合進(jìn)行粘性修正，對(duì)單體復(fù)合船型運(yùn)動(dòng)預(yù)報(bào)方法進(jìn)行研究。

本文利用CFD與勢(shì)流理論結(jié)合的方法，能夠減少大量計(jì)算時(shí)間。通過CFD模擬自由衰減估算粘性力，再以勢(shì)流理論的方法加上粘性力對(duì)波能浮子的幾何形狀進(jìn)行研究，分析平底圓柱浮子的直徑吃水比對(duì)粘性力、運(yùn)動(dòng)響應(yīng)及俘獲寬度比的影響；對(duì)比不同底部角度錐形浮子運(yùn)動(dòng)響應(yīng)及俘獲寬度比，選擇最優(yōu)寬角度。

1 波能浮子數(shù)學(xué)模型的建立

當(dāng)波浪傳遞時(shí)，波能浮子受到波浪作用產(chǎn)生垂蕩作用，使得浮子與PTO產(chǎn)生相對(duì)的位移，進(jìn)而產(chǎn)生能量。因此在數(shù)學(xué)模型建立時(shí)只考慮浮子垂蕩方向的運(yùn)動(dòng)。對(duì)于圓柱形波能浮子，質(zhì)量為m，半徑為a,如圖1。

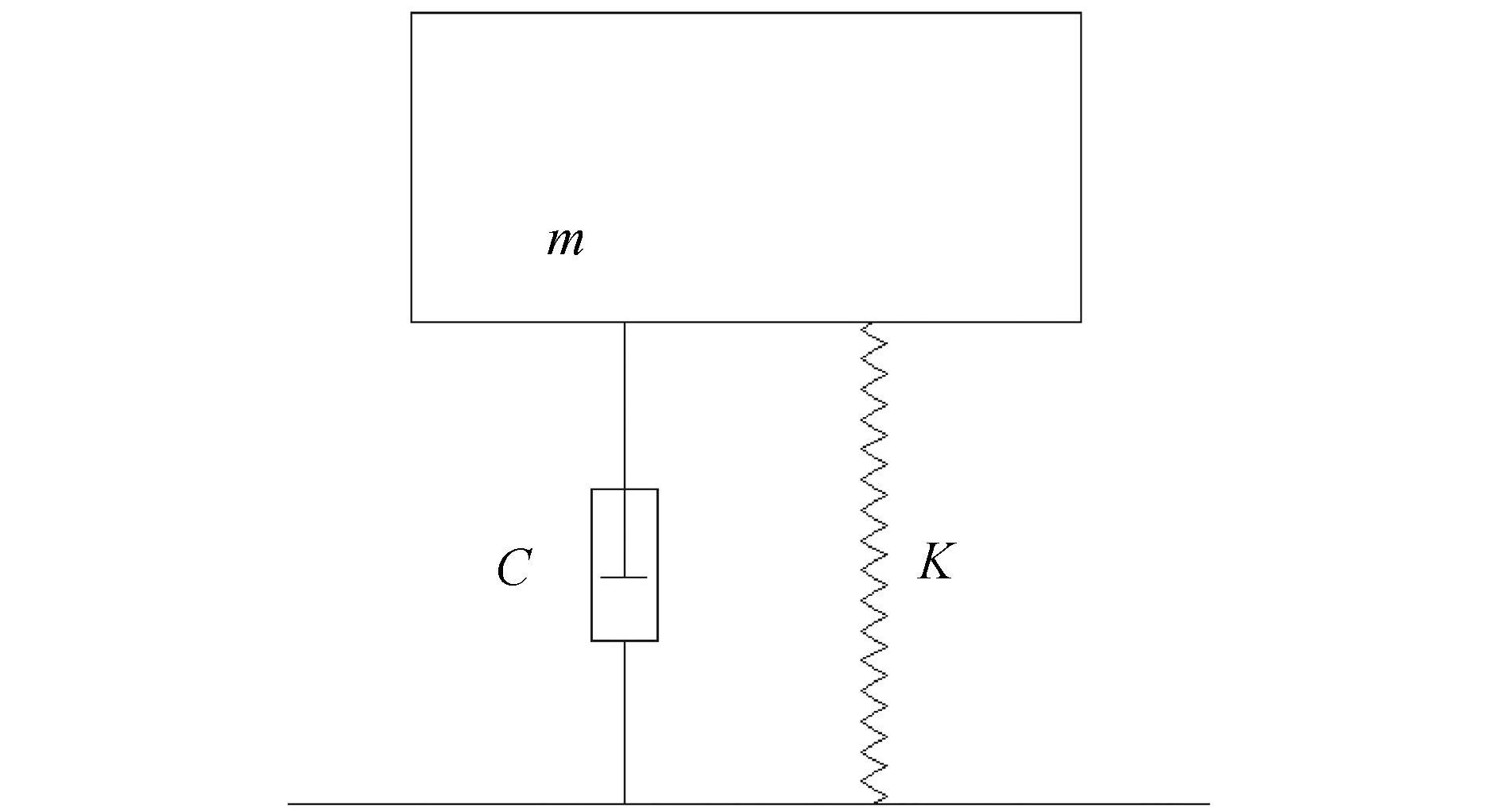
圖1 波能浮子運(yùn)動(dòng)模型

對(duì)于單自由度波能浮子，可用水面浮體的運(yùn)動(dòng)表示，建立運(yùn)動(dòng)方程為：

(1)

(2)

Fs=Cx=ρgπa2x

(3)

(4)

Fk=Kx3

(5)

式中：Fe波浪激勵(lì)力；Fr輻射力；Fs靜水回復(fù)力；Fc線性PTO阻尼力；Fk彈簧力；μ33浮子附加質(zhì)量；λ33浮子輻射阻尼；ρ為水的密度；g為重力加速度；CpPTO阻尼力系數(shù)；K為彈簧系數(shù)。

將各項(xiàng)代入得：

(6)

在線性勢(shì)流理論中，浮子在波浪中運(yùn)動(dòng)時(shí)所受的力可分為入射力、繞射力以及輻射力、入射力和繞射力統(tǒng)稱為波浪激勵(lì)力。在實(shí)際水域中，浮子由于受到粘性影響，其運(yùn)動(dòng)響應(yīng)尤其在共振頻率下遠(yuǎn)遠(yuǎn)小于勢(shì)流理論所得結(jié)果，流體粘性力是導(dǎo)致這一結(jié)果的主要原因。Son等[15]對(duì)圓柱浮子進(jìn)行波浪能裝置實(shí)驗(yàn)時(shí)發(fā)現(xiàn)，勢(shì)流理論所得波浪激勵(lì)力結(jié)果與實(shí)驗(yàn)所測(cè)基本相同，因此，波浪激勵(lì)力項(xiàng)受粘性影響不大。但對(duì)于輻射力項(xiàng)，尤其是阻尼項(xiàng)，試驗(yàn)和勢(shì)流的結(jié)果相差很大，粘性效應(yīng)不可忽略。為了能夠得到浮子的粘性力，Journée等[16]曾通過自由衰減曲線推導(dǎo)浮子的粘性力公式，當(dāng)浮子僅考慮垂蕩運(yùn)動(dòng)時(shí)，其垂蕩自由衰減線性運(yùn)動(dòng)方程為：

(7)

化簡(jiǎn)后得：

(8)

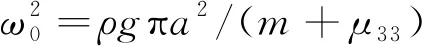
設(shè)無(wú)量綱系數(shù)k：

(9)

(10)

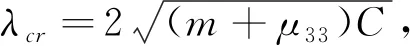
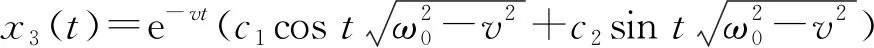
(11)

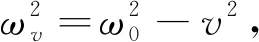
x3(t)=x3,ae-vt[cos(ωvt)+sin(ωvt)]

(12)

設(shè)x3(t)周期為Tv，求解：

x3(t)/x3(t+Tv)=evTv

(13)

化簡(jiǎn)得：

vTv=kω0Tv=ln(x3(t)/x3(t+Tv))

(14)

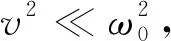
ω0Tv=ωvTv

(15)

繼而可以推導(dǎo)無(wú)量綱阻尼：

(16)

為了防止由于零點(diǎn)漂移原因使得所得數(shù)據(jù)不準(zhǔn)，通過計(jì)算衰減曲線的雙振幅數(shù)值，來(lái)避免這種誤差。

(17)

式中x3,k為第k個(gè)峰值點(diǎn)的幅值。

式(17)能夠通過自由衰減曲線得到無(wú)量綱系數(shù)k，進(jìn)而估算粘性阻尼系數(shù):

λvis=2kρgπa2/ω0

(18)

最終推導(dǎo)出浮子固有頻率時(shí)的粘性阻尼，Tom[17]在實(shí)驗(yàn)中證明，波浪頻率變化對(duì)粘性效應(yīng)影響不大，因此可以通過以上方法算出固有頻率下的總阻尼系數(shù)。結(jié)合Tom的結(jié)論，可以大致計(jì)算出粘性阻尼，從而對(duì)整個(gè)頻域進(jìn)行修正。

浮子粘性阻尼計(jì)算：

λv=λvis-λn

(19)

因此，通過上述論述，得到浮子在垂直方向的運(yùn)動(dòng)方程：

(20)

式中λn為共振頻率下浮子輻射阻尼。

每個(gè)波浪頻率下，浮子的輸出功率存在最優(yōu)阻尼系數(shù)，即cp為某一值時(shí)，輸出功率最大：

(21)

2 數(shù)值模擬方法

利用CFD軟件Star-CCM+來(lái)模擬浮子自由衰減，進(jìn)而算出粘性系數(shù)。模型設(shè)置的是一個(gè)四周壁面的三維水池，浮子自由衰減所興的波會(huì)向四周傳遞，由于水池大小有限，需要考慮壁面效應(yīng)，因此設(shè)置阻尼消波。

模擬中涉及到空氣與水的多項(xiàng)流，應(yīng)用流體體積(VOF)法捕捉空氣相和水相之間的自由表面，因此需要對(duì)液面附近做網(wǎng)格加密，浮子運(yùn)動(dòng)區(qū)域也同樣需要設(shè)置網(wǎng)格加密，并且為了網(wǎng)格尺寸能夠平滑過渡，設(shè)置過渡層。網(wǎng)格設(shè)置如圖2所示：

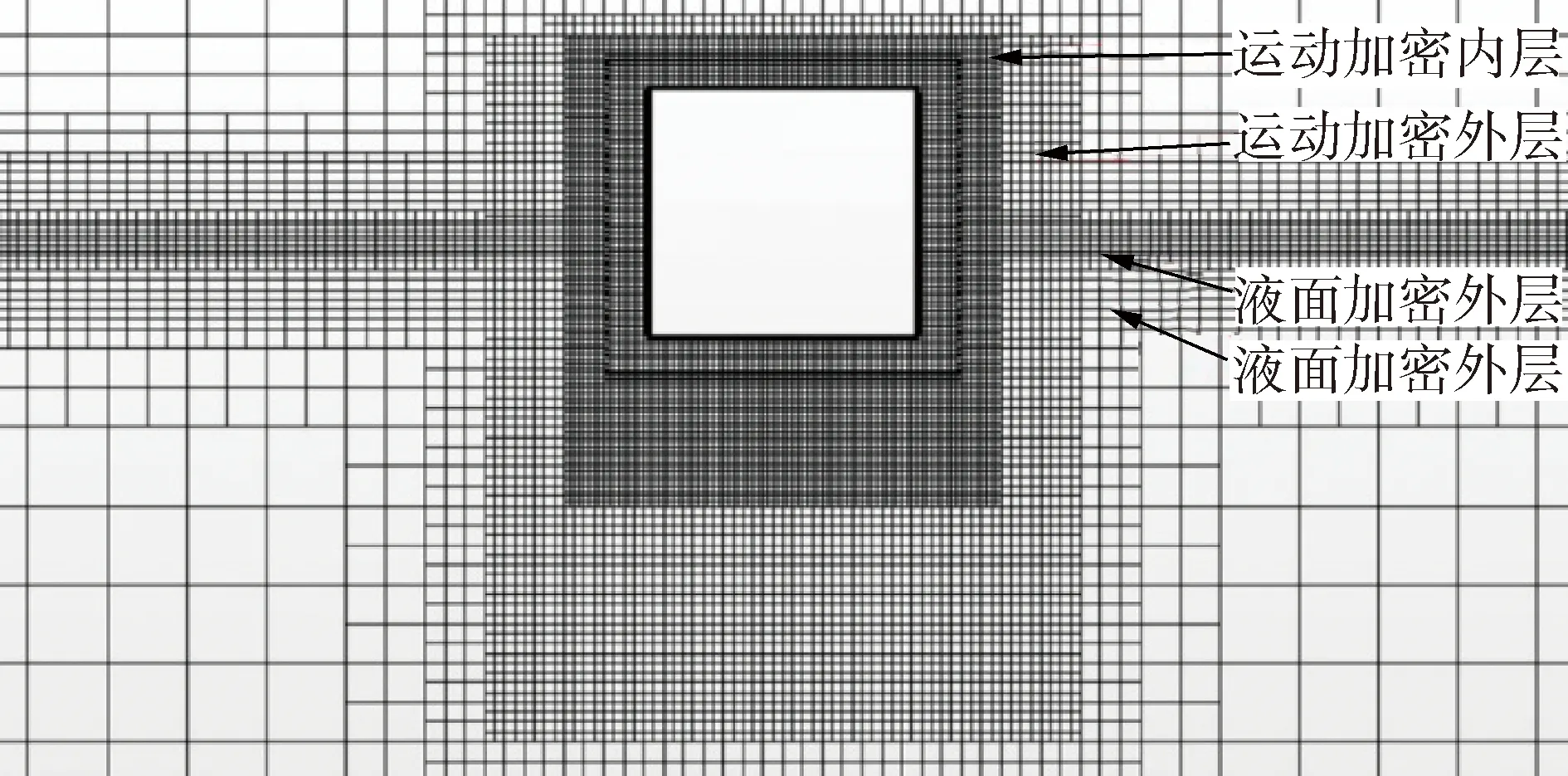
圖2 CFD模型網(wǎng)格劃分

網(wǎng)格劃分及模型設(shè)置是CFD前處理必不可少的，理論上來(lái)講，網(wǎng)格密度越高，計(jì)算精度越高，但同樣計(jì)算時(shí)間會(huì)增加。時(shí)間步長(zhǎng)對(duì)于模擬是否能夠收斂也有很大影響。合適的網(wǎng)格尺寸和時(shí)間步長(zhǎng)對(duì)計(jì)算精度和計(jì)算效率改善有著很好的效果。本文設(shè)置了3個(gè)測(cè)試模型，選擇2a/d=1.6的圓柱浮子，d為浮子吃水，T為浮子共振周期。其時(shí)間步長(zhǎng)和網(wǎng)格大小設(shè)置如表1所示，模擬結(jié)果如圖3所示，根據(jù)3個(gè)模型數(shù)據(jù)得出粘性阻尼，并與模型1對(duì)比得相對(duì)誤差，如表2所示。由表2可知當(dāng)網(wǎng)格及時(shí)間步長(zhǎng)選擇d/30和T/400時(shí)，所得結(jié)果與另外2組相差不大，數(shù)據(jù)差異小于5%，因此d/30和T/400的網(wǎng)格及時(shí)間步長(zhǎng)滿足收斂性要求。

表1 自由衰減模型時(shí)間步長(zhǎng)與網(wǎng)格尺寸設(shè)置

自由衰減模擬除了對(duì)網(wǎng)格大小及時(shí)間步長(zhǎng)收斂性驗(yàn)證以外，還要對(duì)其進(jìn)行準(zhǔn)確性驗(yàn)證。Tom[17]研究了圓柱浮子的水動(dòng)力性能，并做了相關(guān)浮子自由衰減實(shí)驗(yàn)，將CFD數(shù)值模擬所得數(shù)據(jù)與其試驗(yàn)數(shù)據(jù)作對(duì)比。

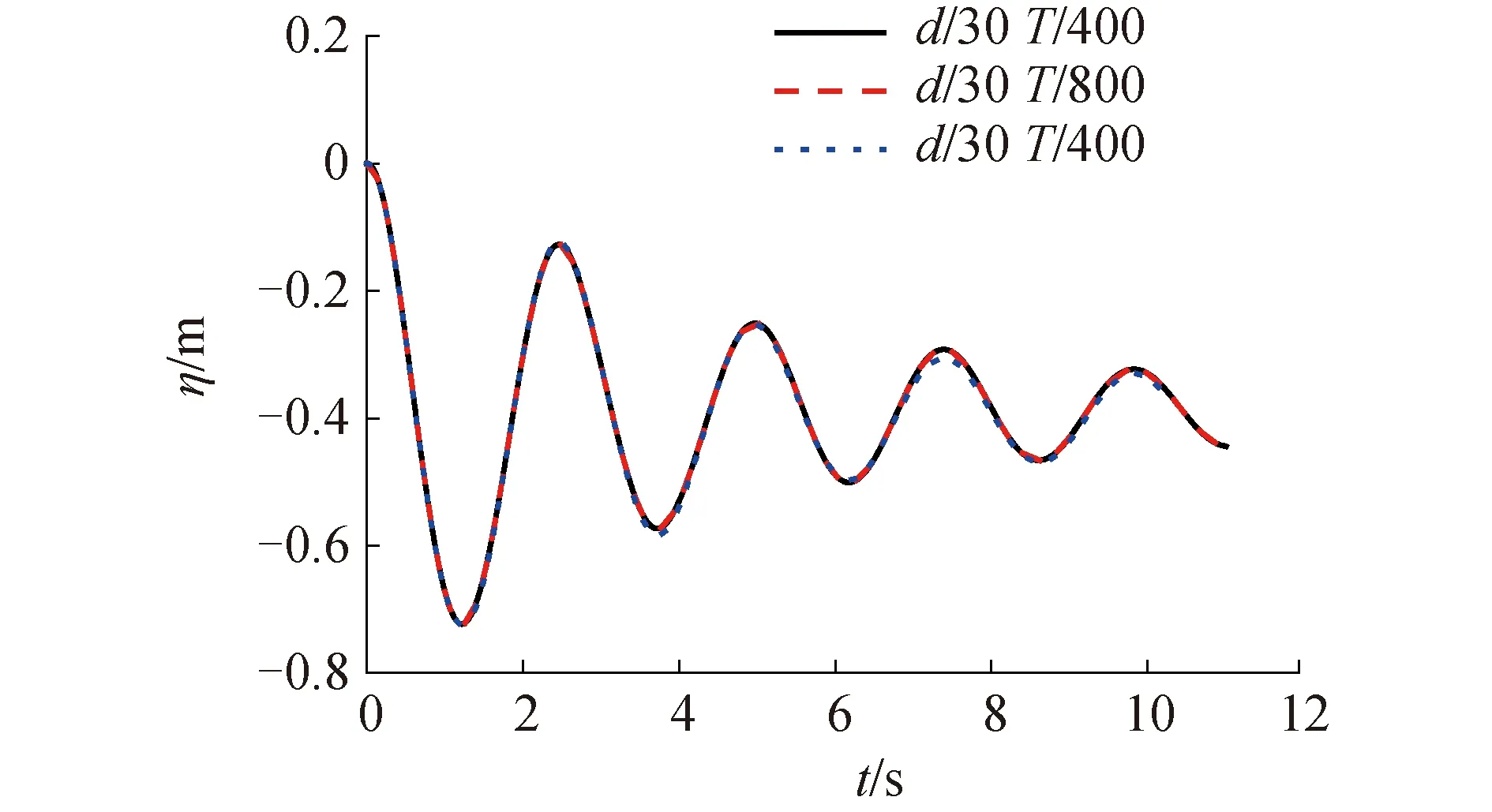
圖3 網(wǎng)格尺寸和時(shí)間步長(zhǎng)收斂性驗(yàn)證

表2 粘性阻尼相對(duì)誤差

觀察圖4，模擬數(shù)據(jù)與實(shí)驗(yàn)數(shù)據(jù)，在周期上幾乎吻合，而在衰減曲線上，實(shí)驗(yàn)數(shù)據(jù)后幾個(gè)周期略大于模擬數(shù)據(jù)，數(shù)據(jù)差別小于5%，驗(yàn)證了數(shù)值模型的準(zhǔn)確性。

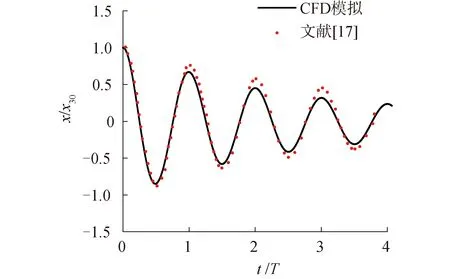
圖4 自由衰減運(yùn)動(dòng)驗(yàn)證

根據(jù)得到的粘性系數(shù)以及推導(dǎo)的運(yùn)動(dòng)方程，求解浮子的頻域運(yùn)動(dòng)響應(yīng)。為了驗(yàn)證其修正數(shù)值的精度，將其與CFD模擬的波浪下浮子運(yùn)動(dòng)作對(duì)比，模型選擇2a/d=1.6的圓柱浮子，周期T=2.17 s，波高H=0.2 m，所設(shè)置阻尼均為最優(yōu)阻尼，得到圖5。

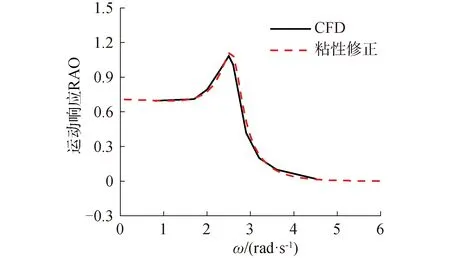
圖5 CFD模擬與粘性修正方法對(duì)比

綜合以上數(shù)據(jù)對(duì)比，基于粘性修正的勢(shì)流理論方法與CFD模擬相比，在共振頻率附近有輕微的差別，垂蕩運(yùn)動(dòng)響應(yīng)結(jié)果基本一致，說(shuō)明可以通過粘性修正方法來(lái)估算浮子運(yùn)動(dòng)，減少計(jì)算量，增加計(jì)算效率。

3 平底圓柱浮子的水動(dòng)力性能分析

由于平底圓柱形浮子幾何特征只有直徑2a和吃水d，因此幾何特征形狀用無(wú)量綱參數(shù)2a/d來(lái)表示。通過改變直徑吃水比，來(lái)改變浮子幾何尺度，更加全面地分析不同尺度浮子的水動(dòng)力性能。為了更好地觀察不同直徑吃水比下浮子的粘性影響，定義阻尼粘性效應(yīng)的無(wú)量綱表示為：

(22)

通過STARCCM++模擬浮子的自由衰減，代入粘性修正公式，并將其無(wú)量綱化，得到不同2a/d下浮子的粘性系數(shù)變化。

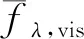
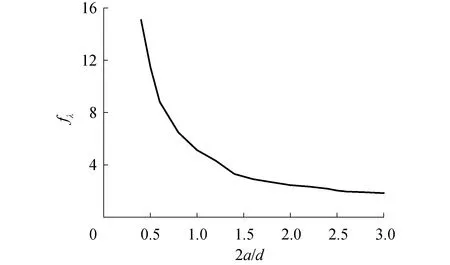
圖6 平底圓柱浮子阻尼修正系數(shù)隨2 a/d變化關(guān)系

圖7中浮子的運(yùn)動(dòng)響應(yīng)峰值隨2a/d的增加而減小，當(dāng)頻率過大或者過小時(shí)，不同比例的浮子運(yùn)動(dòng)響應(yīng)差距不大。當(dāng)ω>2 rad/s左右時(shí)，運(yùn)動(dòng)響應(yīng)開始上升，且2a/d越大上升得越早，同時(shí)下降得也早；當(dāng)ω>5 rad/s左右時(shí)，所有比例基本重合。

圖8中浮子俘獲寬度比(CWR)隨著2a/d的增大其峰值逐漸增加，其所俘獲大功率的頻率范圍也更大，即有效頻域?qū)挾雀蟆４送怆S著2a/d的增加，浮子的峰值所處頻率也在不斷減小，當(dāng)2a/d=0.4時(shí)，峰值點(diǎn)處ω=2.9 rad/s，當(dāng)2a/d=3.6時(shí)，峰值點(diǎn)處ω=2 rad/s，可以通過調(diào)節(jié)尺寸選擇適合海域的浮子。大部分海域都有一段頻繁出現(xiàn)波浪周期。根據(jù)多發(fā)的波浪頻率設(shè)計(jì)相應(yīng)尺寸的浮子，對(duì)于工程應(yīng)用具有重大意義。

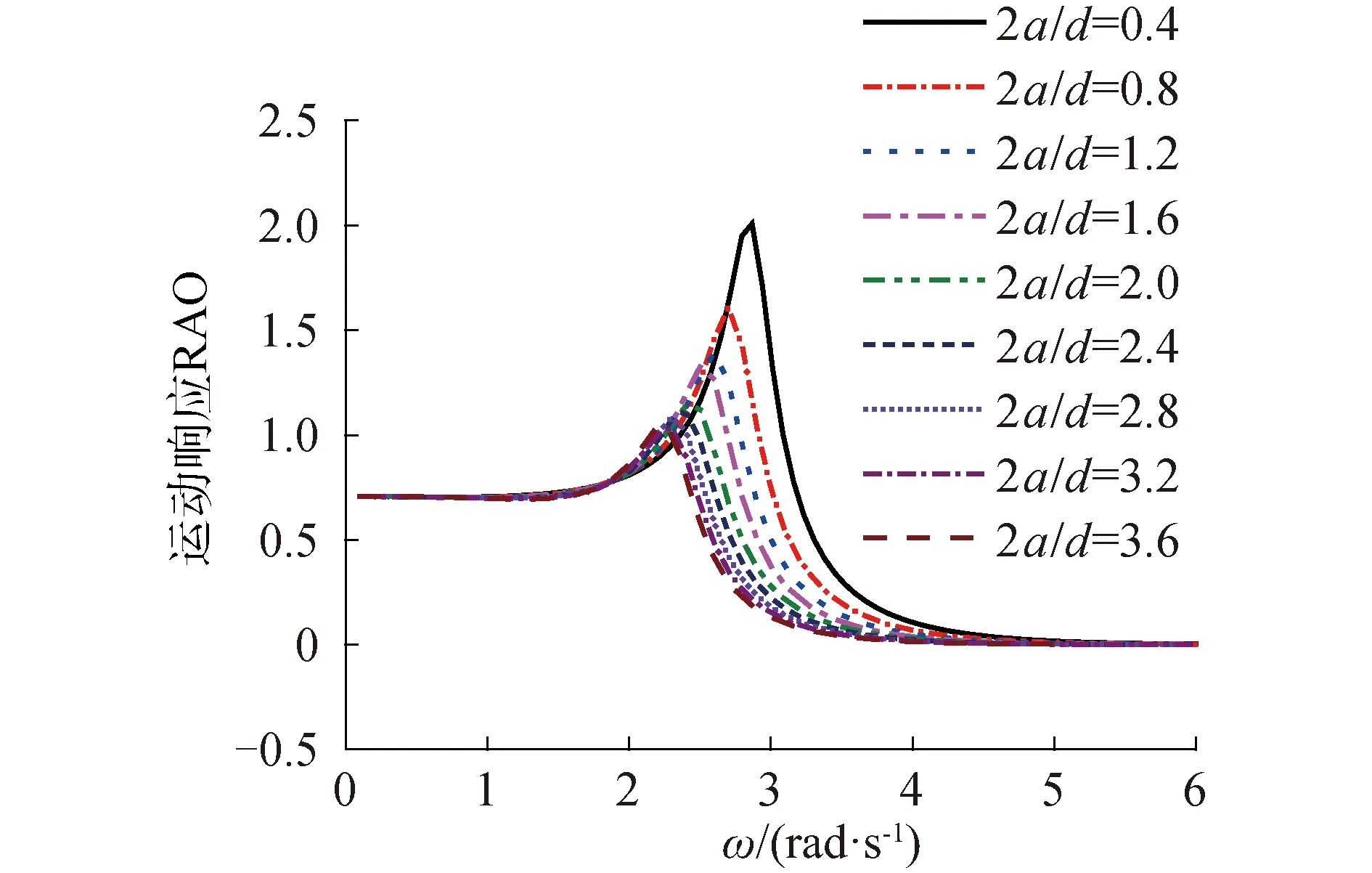
圖7 圓柱浮子頻域運(yùn)動(dòng)響應(yīng)

圖8 圓柱浮子頻域俘獲寬度比

4 錐底浮子的水動(dòng)能性能分析

分析完浮子2a/d對(duì)平底浮子水動(dòng)力性能的影響，接下來(lái)分析錐底浮子底部形狀對(duì)水動(dòng)力性能的影響，選擇4種浮子進(jìn)行分析，分別是α=90°,120°,150°,180°(即平底圓柱浮子),如圖9所示。

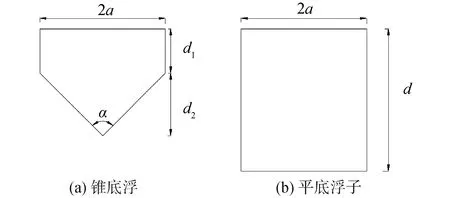
圖9 浮子形狀

選擇尺寸2a/d=1.6，4個(gè)浮子排水體積相同，錐底浮子的等效吃水與平底圓柱浮子的相同。

由圖10可知阻尼修正系數(shù)隨著角度的增大而增大，即底部形狀的角度越小所受粘性影響越小。計(jì)算浮子的運(yùn)動(dòng)響應(yīng)以及俘獲寬度比，由圖11可以觀察到，不同錐底角度的浮子，其共振頻率有細(xì)微的變化，當(dāng)角度變小時(shí)，因?yàn)樾〗嵌儒F底浮子所受粘性影響小，其運(yùn)動(dòng)響應(yīng)就隨之增大。觀察俘獲寬度比變化圖可知隨著角度的減小，其俘獲寬度比的峰值增大，且有效頻域?qū)挾纫搽S之增大，更加有利于對(duì)波浪功率的俘獲,如圖12所示。然而在工程實(shí)際利用中，當(dāng)錐底角度越來(lái)越小，為保證其排水體積不變，長(zhǎng)度就會(huì)隨之增加，不利于浮子的安裝以及整個(gè)裝置的運(yùn)行，因此，對(duì)于適合角度的錐底浮子需要根據(jù)實(shí)際情況決定。

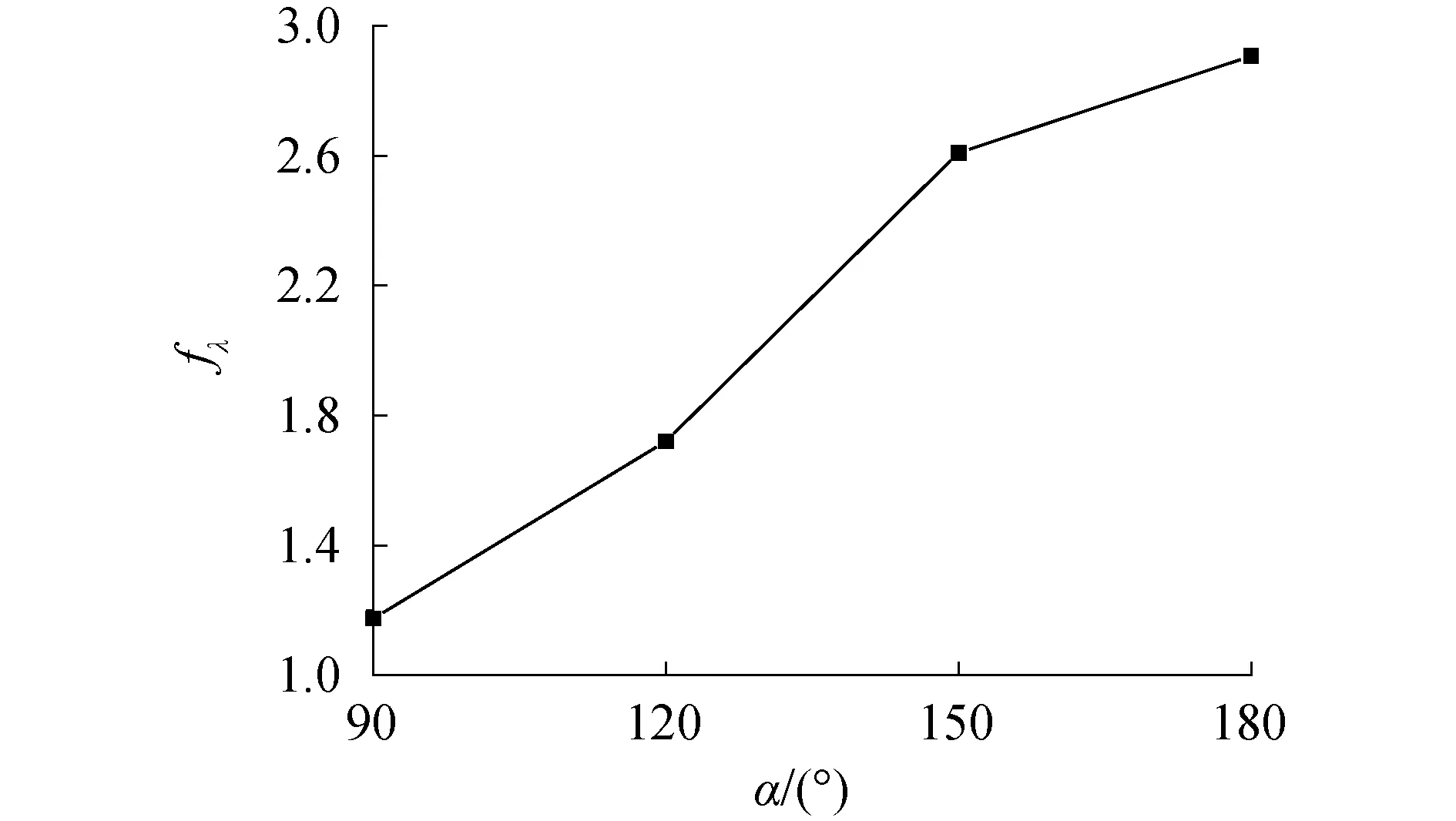
圖10 浮子阻尼修正系數(shù)隨底部角度變化關(guān)系

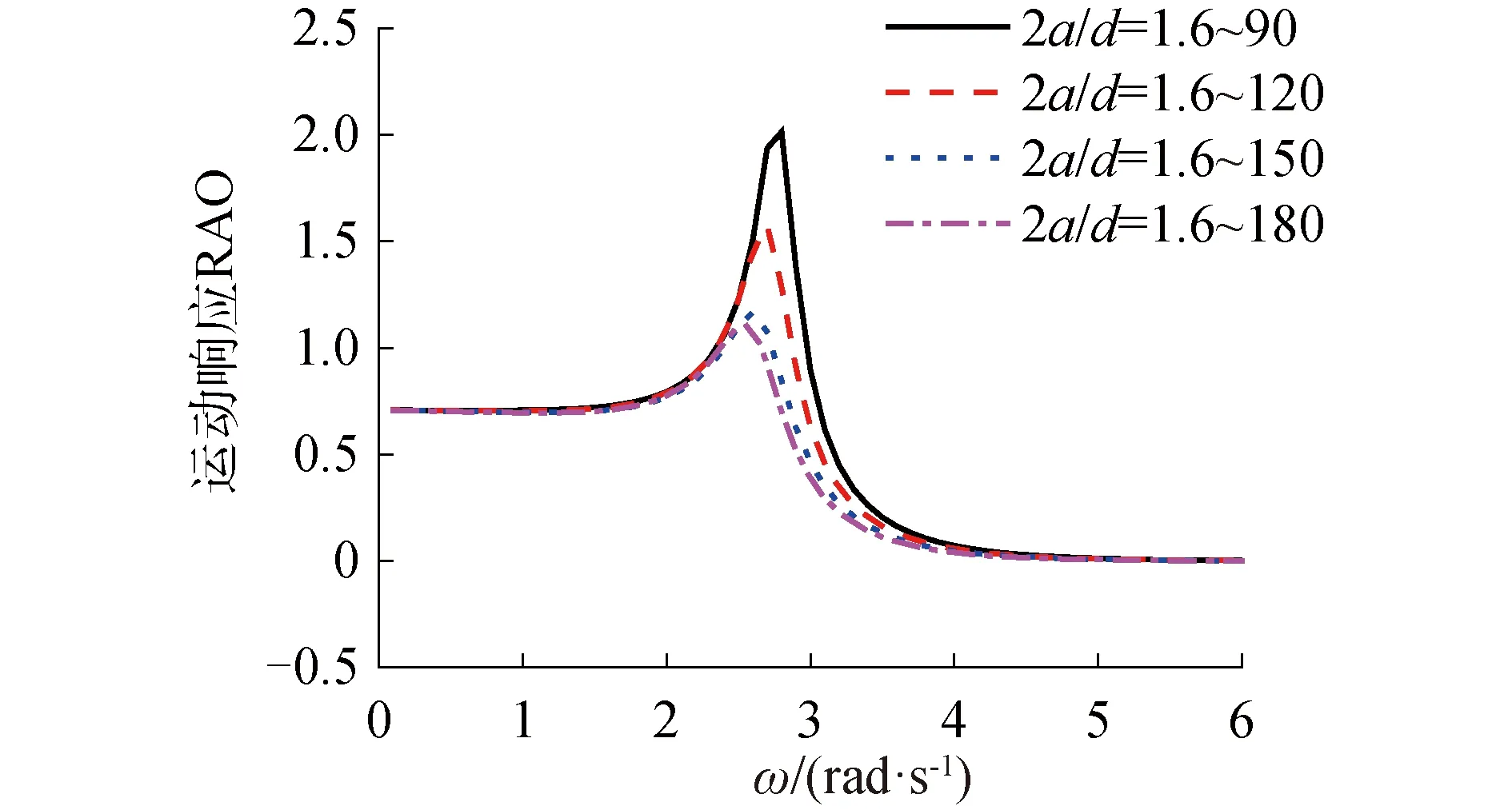
圖11 不同底部形狀浮子運(yùn)動(dòng)響應(yīng)

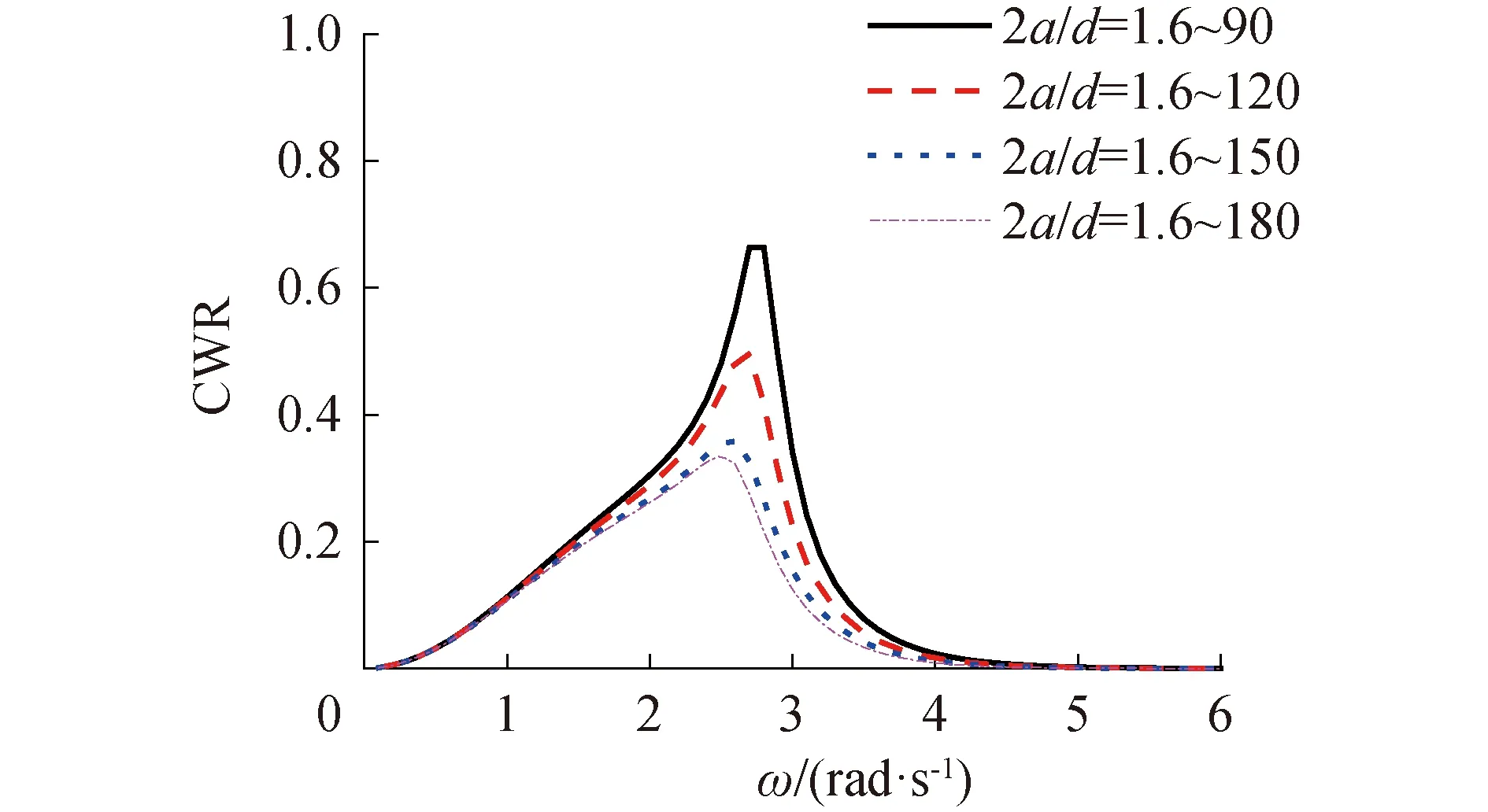
圖12 不同底部形狀浮子俘獲寬度比

在使用粘性修正的方法計(jì)算浮子水動(dòng)力系數(shù)后，為保證數(shù)值模擬的準(zhǔn)確性，需要利用CFD方法進(jìn)一步分析計(jì)算，通過模擬浮子在波浪下的運(yùn)動(dòng)流場(chǎng)，分析流場(chǎng)結(jié)構(gòu)和變化機(jī)理，進(jìn)一步檢驗(yàn)線性計(jì)算結(jié)果的可靠性。本文利用Star-CCM+模擬4個(gè)浮子在共振周期附近的波浪下的運(yùn)動(dòng)，監(jiān)測(cè)其流場(chǎng)渦的變化，波浪為從右向左傳遞。

由圖13～16為4個(gè)浮子在在一個(gè)周期內(nèi)的浮子周圍渦量場(chǎng)圖，不難看出，迎著波浪的這一側(cè)會(huì)產(chǎn)生較大的渦，因?yàn)槭艿礁∽幼璧K的流體與波浪傳遞過來(lái)的流體之間產(chǎn)生了較大的速度梯度，從而產(chǎn)生了渦。圖中，浮子錐底角度越大，附近渦量分布越紊亂，渦分布的范圍越大，其中90°錐底浮子渦分布范圍很小，僅在浮子下方有一部分，而180°平底浮子流場(chǎng)渦分布范圍最廣。這也就會(huì)導(dǎo)致波浪能能量的耗散增加，影響浮子對(duì)能量的吸收，進(jìn)而影響效率。可以看出，主要產(chǎn)生渦的部位是圓柱轉(zhuǎn)為圓錐處的拐角，這是因?yàn)閹缀纬叽缤蝗蛔兓瑢?dǎo)致流體的速度梯度也變大，容易產(chǎn)生渦。并且錐底角度越大，其尺寸變化幅度也就越大，所產(chǎn)生的大量級(jí)的渦也越多，這說(shuō)明波浪能量通過浮子壁面將能量傳遞給了流體質(zhì)點(diǎn)，變成了流體質(zhì)點(diǎn)的動(dòng)能。意味著運(yùn)動(dòng)過程中耗散的能量增加，這些耗散的能量無(wú)法被吸收，而入射波能量固定，這就導(dǎo)致錐底角度小的浮子能量利用率高于角度大的浮子。

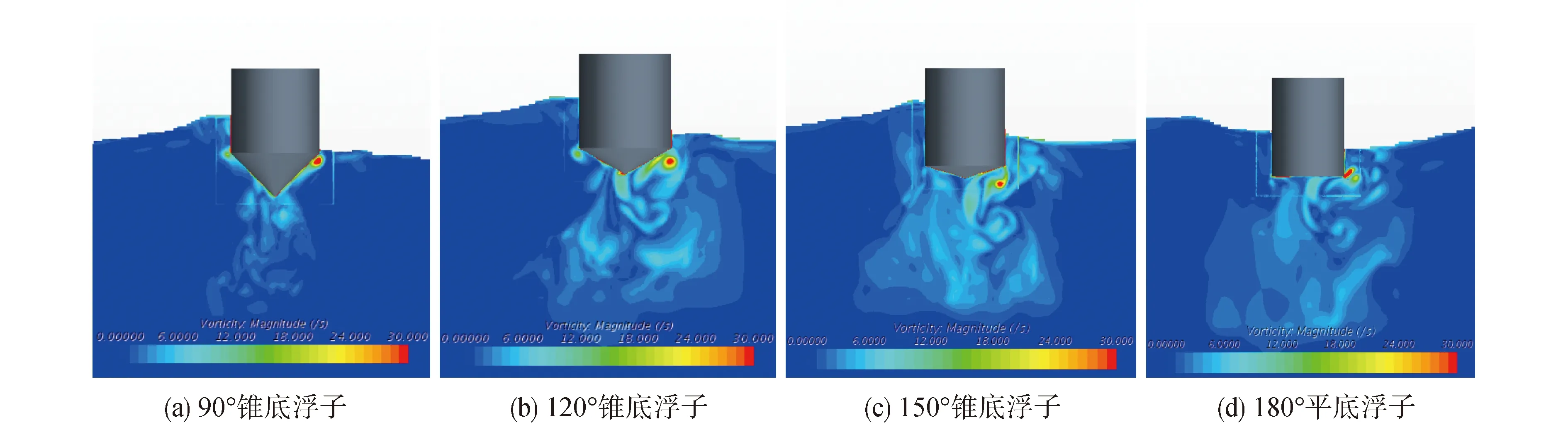
圖13 各浮子在t=NT+T/4時(shí)的渦量場(chǎng)

圖14 各浮子在t=NT+T/2時(shí)的渦量場(chǎng)

圖15 各浮子在t=NT+T3/4時(shí)的渦量場(chǎng)

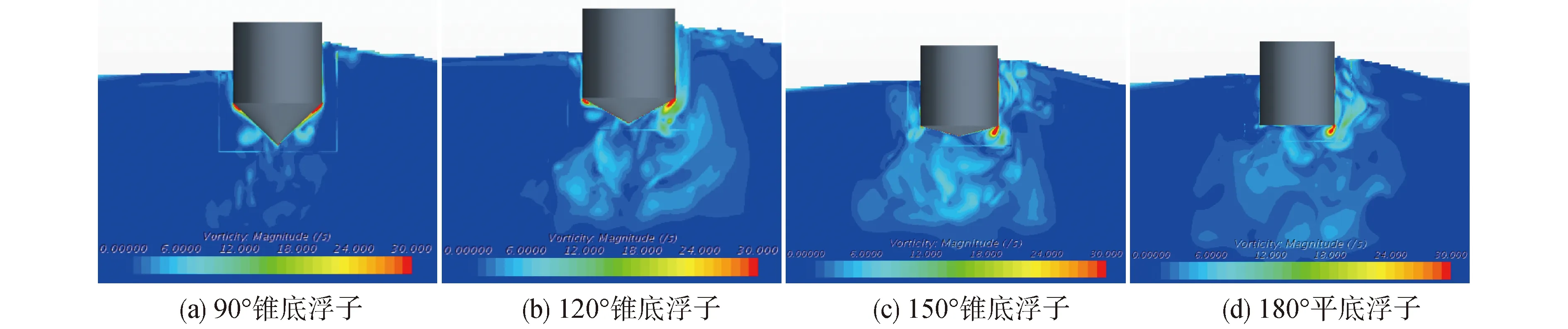
圖16 各浮子在t=(N+1)T時(shí)的渦量場(chǎng)

5 結(jié)論

1) 對(duì)于平底圓柱浮子，研究了不同直徑吃水比的粘性阻尼大小及水動(dòng)力性能，圓柱浮子越矮胖，其所受粘性阻尼越小，并且隨著2a/d的增大，浮子俘獲寬度比的峰值區(qū)域也會(huì)改變。

2) 對(duì)于錐底圓柱浮子，分析了不同錐底角度浮子的水動(dòng)力性能，當(dāng)錐底角度較小時(shí)，更有利于浮子對(duì)波浪能量的俘獲。

3) 通過對(duì)浮子進(jìn)行時(shí)域流場(chǎng)分析，得到錐底角度大的浮子容易產(chǎn)生較大范圍及量級(jí)的渦，影響波浪能量的吸收,與頻域分析結(jié)果一致。