海洋混響數據的SαS分布建模

王平波， 衛紅凱， 婁良軻， 代振

(海軍工程大學 電子工程學院，湖北 武漢 430033)

在傳統的聲吶信號處理中，高斯模型占據著主導地位。隨著現代主動聲吶體制向低頻、大功率、大孔徑方向發展，混響對聲吶性能的影響日趨嚴重，如何有效地抑制混響干擾成為主動聲吶信號處理的首要任務。大量實踐表明，沿襲傳統的高斯分布假設，往往不能取得理想的抗混響效果。因此，放棄高斯假設而采用非高斯分布假設在水聲信號處理業界已成為一種趨勢[1-2]。 近年來，α穩定分布作為一種非高斯分布模型，具有統計分布的穩定性和概率密度函數(probability density function，PDF)的代數拖尾特點，在信號處理領域受到了廣泛的重視，己成為常用的沖激信號統計模型[3-7]。作為唯一的一類構成獨立同分布隨機變量之和的極限分布[4]，α穩定分布是廣義的高斯分布，通過調整特征指數α的值實現對PDF拖尾厚度的控制，可以對PDF為單峰鐘形隨機信號統計特性進行靈活地描述，比高斯分布具有更廣泛的適用性。而以混響為主的主動聲吶背景干擾，其瞬時幅度樣本是均值為零、正負樣本量大致相等、上下包絡線基本對稱的隨機信號[1-2]，即其PDF恰好是以0為中心左右對稱的單峰鐘形曲線。因此，本文將原點位置對稱α穩定分布(SαS, symmetric alpha-stable distribution)引入到混響非高斯PDF建模中，并使用仿真和實測數據對這一建模方法的可行性和正確性進行檢驗，最后通過大量海試混響數據建模結果分析，對混響數據的SαS分布規律進行歸納總結。

1 混響的特點與SαS分布簡介

1.1 混響數據的特點

海洋混響是海洋信道中一切散射作用的總和。從瞬時幅度上看，它是緊跟在發射之后、總體由強至弱的一連串衰減(可能還有起伏震蕩)波形。

圖1給出了一段典型的主動聲吶陣元級接收數據波形，從中可以分析歸納混響數據的一般特點。

引發這段數據的發射信號是4 s脈寬的HFM脈沖。前4 s為發射脈沖直達聲，稱為直達聲區。事實上，發射伊始即引發混響，亦即，直達聲區中也有不完整發射脈沖引發的混響，但因其混疊于直達聲中難以分離，且此處視為主動聲吶近程盲區，一般不對其內的混響進行研究。直達聲結束后，數據幅度從與直達聲等高度逐漸衰減，直至不再明顯降低，大致如圖中的4～12 s段所示，這一段是典型混響區域，稱為混響限制區，該區域內，混響強度高于背景噪聲，是聲吶的主要背景干擾。大致從12 s向后，混響淹沒于背景噪聲之中，以海洋環境噪聲為主的背景噪聲成為主要的背景干擾，混響的影響可以忽略，而背景噪聲是寬平穩的，故接收數據幅度不再明顯變化，此段稱為噪聲限制區。根據聲吶量程，噪聲限制區可以延續很長，這里僅給出一部分。不難理解，研究混響數據的統計特性，要基于混響限制區內的數據進行。

從圖1中還直觀可見，混響數據是0均值的、正負樣本量大致相等、上下包絡線基本對稱，這意味著，可以使用0均值對稱單鐘型曲線來對混響數據的概率密度函數進行擬合建模。零均值高斯分布、混合高斯分布，和下面要介紹的SαS分布，其PDF恰好就是這樣一類曲線。

1.2 SαS分布簡介

若隨機變量X具有如下形式的特征函數[3]：

φ(t)=E[exp(itX)]=

exp{iμt-γ|t|α[1+iβsgn(t)ω(t,α)]}

(1)

則稱X服從α穩定分布，記為X～S(α,β,γ,μ)。其中，

式中：α為特征指數，表征穩定分布脈沖特性強弱，α∈(0,2]，值越小，則所對應分布的拖尾越厚，非高斯脈沖特性越顯著；γ為離差，亦稱為尺度參數、分散系數，表征穩定分布隨機變量偏離其均值或中值的程度，γ∈(0,∞)，定義σ=γ1/α為標準離差；β為偏斜指數，表征穩定分布的偏斜程度，β∈[-1,1]，β=0、β>0和β<0時，分別對應穩定分布無偏斜(對稱)、右偏斜和左偏斜情況；μ為位置參數，表征穩定分布的均值(α>1時)或中值(α≤1時)，μ∈(-∞,∞)。

α穩定分布特征函數與其PDF是一對傅立葉變換[3]，可通過對特征函數進行傅立葉變換得到PDF：

f(x;α,β,γ,μ)=

(2)

除幾組特殊參數取值外，式(2)一般沒有封閉的解析表達式，需要以數值積分方式計算[8-9]。圖2給出了以這種方式計算繪出的不同參數取值時的α穩定分布的PDF曲線比較。從各圖中參數變化時的PDF曲線對比，可以清晰地看到對應參數的物理意義體現。

一些常見分布可以看作是α穩定分布S(α,β,γ,μ)的特例[3]，比如：當α=2、β=0時，S(2,0,γ,μ)就是高斯分布(μ,2γ)；當α=1、β=0時，S(1,0,γ,μ)就是柯西分布(μ,γ)。

當偏斜指數β=0時，α穩定分布稱為對稱α穩定分布，記為SαS分布。不難發現，高斯分布、柯西分布都是SαS分布的特例。正常狀態下的主動聲吶背景干擾數據，包括混響數據，其樣本都是無偏斜且0均值的，故可用位置參數μ=0的SαS分布來擬合其PDF，可把這種分布稱為原點位置SαS分布，簡記作Sα(γ)。

可以看到，Sα(γ)分布僅有2個參數：特征指數α和離差γ，就像常用的高斯分布一樣簡潔。值得指出，在對混響數據進行非高斯PDF建模時，堪用的模型，即使最簡潔的二階0均值混合高斯模型ZMGM(2)，也有3個參數[1]。相對少的參數意味著相對快捷而精確的參數估計算法，在這一點上，Sα(γ)具有無可比擬的優勢。

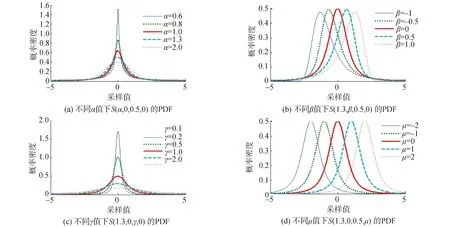
圖2 不同參數下的S(α,β,γ,μ)分布PDF變化

2 混響數據SαS分布建模方法

獲取合格而足量的混響樣本數據后，即可以原點位置SαS分布對其進行建模。而建模的核心任務是，如何構建Sα(γ)的2個未知參數α和γ估計器。

一般的α穩定分布S(α,β,γ,μ)參數估計問題，已經有很多文獻研究[3,8，10]。如前分析，混響數據實際上可以簡化的α穩定分布，即Sα(γ)分布進行PDF建模，故針對這一特點，本文從諸多方法中予以選取并簡化改進，建立了如下2種方法：正負矩法和對數矩法。

2.1 正負矩法

設隨機變量X～Sα(γ)，則有[3]：

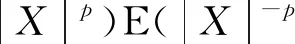
(3)

式中：

M|X|(p)?E(|X|p)=C(p,α)γp/α

(4)

(5)

這里，Γ(·)為伽馬函數，定義為[8]：

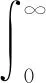
(6)

由式(3)～(5)，有：

(7)

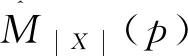
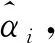
2.2 對數矩法

設隨機變量X～Sα(γ)，則由式(4)有：

E(|X|p)=E(epln|X|)=C(p,α)γp/α

(8)

引入負階矩和分數階矩概念后，式(8)在p=0處連續[3]。定義隨機變量Y=ln|X|，則Y的矩母函數為：

(9)

故Y的任意k階矩都是有限的，且滿足：

(10)

k=1時可得Y的一階原點矩(均值)為:

(11)

式中ce為Euler常數。同理可得Y的二階中心距(方差)為：

(12)

應當指出，式(11)與(12)中已無矩母函數自變量(亦即正負矩法的中階數)p，這就是說，對數矩法不需要p初值設定，恰與正負矩法形成補充，二者估計結果可以相互印證。

2.3 仿真實例

首先使用PDF可設定的仿真數據檢驗Sα(γ)分布對高斯和非高斯PDF的擬合能力。

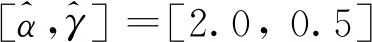
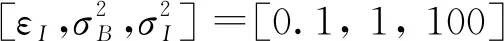
圖4 SαS分布Sα(γ)對非高斯數據PDF的擬合性能

3 混響數據的SαS分布特性分析

本節以數組低頻主動拖曳線列陣聲吶(0411三亞海試)數據分析為例，驗證以混響為主的主動聲吶背景干擾數據(即圖1所示中的混響限制區內數據，簡稱為混響)SαS分布PDF建模方法的正確性，并初步歸納混響PDF的SαS分布規律。

3.1 建模方法驗證

(0411三亞海試)發射3種主動脈沖信號：Ⅰ表示脈寬為432 ms、頻率為750 Hz的CW脈沖，稱為窄帶短脈沖；Ⅱ表示同樣脈寬、頻帶為650～850 Hz的LFM脈沖，稱為寬帶短脈沖；Ⅲ表示脈寬為1 296 ms、同樣頻帶的LFM脈沖，稱為寬帶長脈沖。使用80元拖曳線列陣接收回波數據。進行PDF建模前數據已經過帶通濾波→波束形成→移頻→降采樣→幅值歸一化等處理[1,11]。

圖5～7分別給出了3段3種脈沖混響數據的波形圖和SαS分布PDF建模擬合圖。為便于比較，圖5～7(b)圖中同時繪出了：① 使用柱狀圖統計法得到的PDF曲線，圖中標記為HS。在足夠樣本量下，HS曲線可視為真實分布。② 使用正負矩法Sα(γ)參數估計得到PDF擬合曲線，圖中標記為NM。③ 使用對數矩法Sα(γ)參數估計得到PDF擬合曲線，圖中標記為LM。NM和LM方法得到的α、γ參數估計值也同時標記于圖5～7(b)圖上方。

圖5 一段窄帶短脈沖混響數據SαS分布驗模

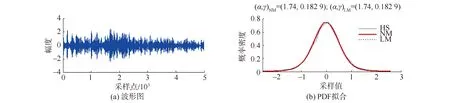
圖6 一段寬帶短脈沖混響數據SαS分布驗模

圖7 一段寬帶長脈沖數據SαS分布驗模

由圖可見，負階矩法、對數矩法2種參數估計方法得到的參數估計值幾乎完全相同，擬合的NM和LM曲線幾乎完全重合。而此二者又與統計得到的HS曲線幾乎完全重合。這說明，這2種參數估計方法具有幾乎完全相同的PDF建模精度，都能夠真實反映數據的PDF特性。換言之，SαS分布Sα(γ)可以精確反映混響數據的PDF，其參數估計選用正負矩法或對數矩法皆可。從運算速度看，對數矩法略優。下文選用對數矩法。

3.2 建模結果分析

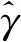
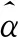
表1 海試混響數據α估值分布區間統計

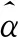
4 結論

1)SαS分布可對主動聲吶背景干擾進行較好的概率密度擬合；

2)在混響限制區內，主動聲吶背景干擾的特征指數α近半數集中在1.6～1.9，表現出一定的非高斯性。