高速鐵路陡坡路基h型樁板墻關鍵設計參數分析

廖 超

(中鐵第四勘察設計院集團有限公司,武漢 430063)

引言

我國是個山區面積廣大的國家，山區地勢起伏大，地面橫坡陡，而且這些地區構造、侵蝕作用強烈，地質條件復雜。隨著高速鐵路的蓬勃發展，出現了大量的高速鐵路陡坡路基工程，在這種情況下，提高線路的橋隧比例能夠有效減少陡坡路基。但是在同等條件下，橋隧造價比路基要顯著增加，而且工程建設的難度也將成倍增大。因此，根據現場實際情況，采用適用于陡坡路基地段的支擋結構，達到既能有效收縮坡腳、確保路堤穩定，又能降低工程造價的目的。高速鐵路對路基的沉降變形有嚴格的要求，對于陡坡路基，一般采用重力式擋墻、樁板墻[1]及樁基托梁[2]等支擋方式進行邊坡加固。但邊坡較高或土壓力較大時可能難以滿足檢算要求。對于公路工程當常用的支擋結構不能滿足要求時，可采用預應力錨索樁進行陡坡路基加固[3-5]。由于預應力錨索對垂直錨索方向的受力特別敏感，預應力錨索樁板墻用于路堤支擋，存在填料下沉產生次生應力的可能，因此，鐵路路基一般不采用預應力錨索樁板墻用于陡坡路堤邊坡加固。

h型樁板墻是一種組合樁結構，由主樁、副樁、橫梁、承載板及擋土板組成[6]，具有較強的水平荷載承載能力及較大的剛度，能有效控制邊坡穩定及水平位移[7-8]，可用于滑坡及陡坡地段的邊坡加固工程，已在鐵路[9]和公路[10]陡坡路基中取得成功運用。目前不少學者對該結構的理論計算方法[11-12]、變形控制[7-8]、設計方法[13]及力學特性[14-19]等進行了研究，取得了大量的成果，但是均未對相關設計參數進行深入的研究[20]。本文建立大量的計算模型，分別對錨固段為土質地層及巖質地層提出關鍵設計參數建議值。

1 計算方法

h型樁板墻橫梁位于線路內側，受力機理為邊坡的土壓力首先直接作用于副樁上，然后再通過橫梁及樁排間巖土體傳到主樁上，同時上部土體土壓力直接作用于主樁懸臂段，最后形成副樁、橫梁、樁間巖土體、主樁四位一體共同抵抗土壓力[15-19]。根據內力分析，橫梁上可選擇設置或不設置承載板。h型樁板墻如圖1所示。

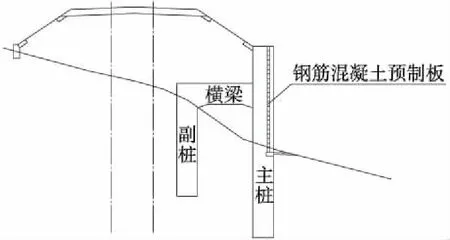
圖1 h型樁板墻示意

h型樁板墻可分解為h型抗滑樁及擋土板兩部分，h型抗滑樁可進行平面簡化，采用結構分析軟件進行計算，將荷載作用在平面桿件上，分別計算各部件的內力與變形，建立的模型應考慮地基土剛度對樁的影響，即地基土與樁的相互作用，可采用節點彈簧進行模擬。

1.1 結構荷載計算[11]

(1)主樁懸臂段土壓力作用計算方法

h型樁板墻上部懸臂部位類似樁板墻結構，墻面水平土壓力按主動土壓力考慮，列車荷載產生的水平壓力按彈性理論土中應力分布原理計算，兩項水平壓力疊加后簡化呈梯形或三角形分布。

P1=kaql

(1)

P2=kaql+kaγh1l

(2)

式中，ka為主動土壓力系數；h1為長樁懸臂段長度，m；l為結構縱向跨度，m；γ為上部填土重度，kN/m3。

(2)橫梁上側土壓力作用計算方法

橫梁上側土壓力計算可將橫向樁間距范圍內的土自重及上部荷載施加在橫梁上，計算方法見式(3)。

P=ql1+γh1l1

(3)

式中，P為橫梁上均布荷載，kN/m；γ為上部填土重度，kN/m3；h1為填土高度，m；l1為橫向樁間距，m；q為列車均布荷載，kN/m。

(3)橫梁下側土壓力作用計算方法

考慮到h型樁板墻在使用階段隨著地基土自然沉降，由于結構和土體的剛度差異，底部土體對承載板與橫梁的支撐作用將逐漸減弱甚至可能出現脫離現象，所以在設計中視其為安全儲備，計算中不考慮底部土體的支撐作用。

計算荷載分布示意如圖2所示。

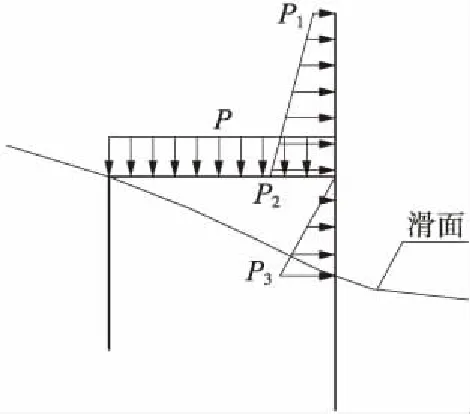
圖2 荷載示意

1.2 樁側土作用的模擬

按文克勒假定，樁側土作用在樁上的抗力可以用式(4)表示。

P=khb0x

(4)

式中，b0為樁的計算寬度，m；x為樁身截面的橫向位移，m；kh為土的橫向抗力系數，kN/m3。

土的橫向抗力系數kh沿樁身的分布規律根據地質情況采用“m”法或“k”法，采用“m”法時kh=mz。

模型中，沿單樁樁體每米分割為一個節點，建立節點彈簧，彈簧剛度kz計算如式(5)。

kz=mzb0×103

(5)

式中，kz為彈簧剛度，kN/m；m為地基系數的比例系數，MN/m4；z為樁截面深度，m。

2 工程案例

杭黃鐵路存在大量的陡坡路基，其中DK69工點采用h型樁板墻支擋。

2.1 工程地質及水文地質條件

地層巖性及土石等級：

(4)-1 D1-2t粉砂巖，褐黃色，全風化，Ⅲ，σ0=250 kPa；

(4)-2 D1-2t粉砂巖，灰黃色，強風化，Ⅳ，σ0=450 kPa；

(4)-3 D1-2t粉砂巖，青灰色，弱風化，Ⅴ，σ0=700 kPa。

水文地質條件：地下水主要為基巖裂隙水，基本不發育。區內地下水無二氧化碳侵蝕、硫酸鹽侵蝕、有酸性侵蝕，化學環境作用等級為H1；僅根據氯離子含量判定，地表水、地下水均無氯鹽侵蝕。

地震動參數：地震動峰值加速度為0.075g，地震動反應譜特征周期(中硬土)為0.35 s。

2.2 設計概況

工點最不利斷面右側路肩距坡腳高差為18.9 m，采用內置式h型樁板墻支擋，為減小自由段長度，采用路堤墻形式。樁頂路堤邊坡高4 m，主樁自由段長14.9 m、錨固段長11.1 m，副樁長10 m，主副樁橫向凈間距9 m，縱向間距(中心)6 m。樁基及橫梁截面均為2 m×2.25 m，橫梁設置在距主樁樁頂4 m處，橫梁右側懸空處設置承載板，設計斷面如圖3所示。

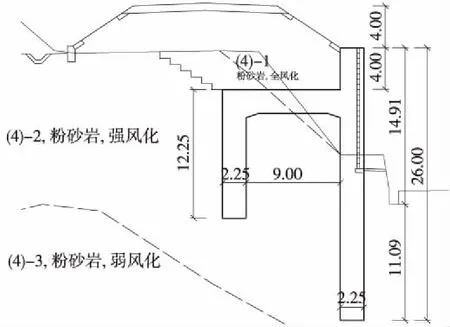
圖3 試驗工點設計斷面(單位：m)

3 關鍵設計參數影響分析

3.1 計算模型

采用數值計算軟件，建立平面桿件彈性計算模型。樁基及橫梁之間剛性連接，截面尺寸為2 m×2.25 m，沿線路方向樁間距6 m。錨固段采用節點彈簧模擬樁土作用，彈簧剛度根據表1中土質及巖質地層的地基參數，采用式(5)進行計算，樁底按鉸支考慮。施加于計算模型的橫梁及主樁上荷載參照式(1)～式(3)計算。

3.2 計算參數

h型擋墻及擋土板采用C35混凝土，計算參數見表1。

表1 材料計算參數

3.3 計算結果分析

3.3.1 橫梁設置位置對結構的影響

分別建立錨固段為巖質及土質地層、橫梁距樁頂距離為3～8 m的計算模型，分析各計算模型的受力情況，提取結構各部件的力學指標，對結構進行分析總結。代表性內力曲線如圖4～圖7所示。

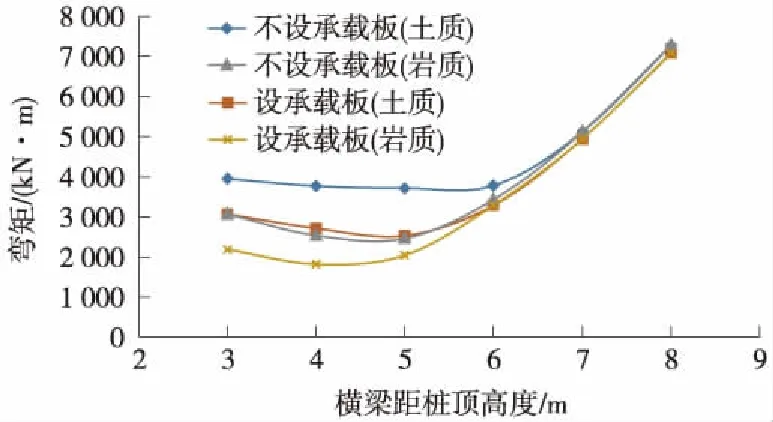
圖4 主樁最大彎矩與橫梁位置的關系曲線

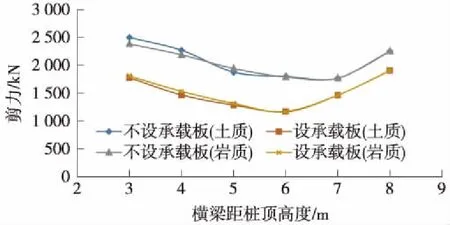
圖5 主樁最大剪力與橫梁位置的關系曲線

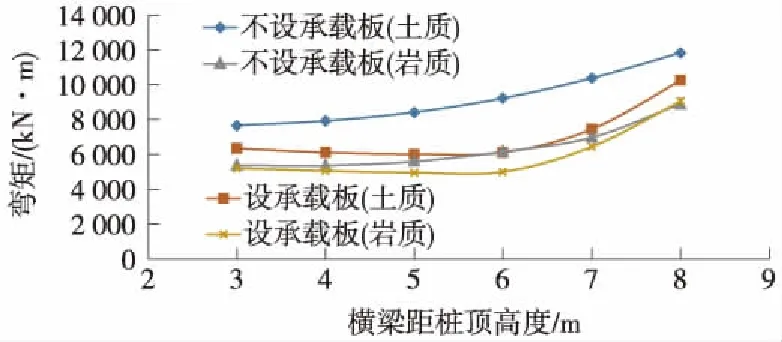
圖6 橫梁最大彎矩與橫梁位置的關系曲線

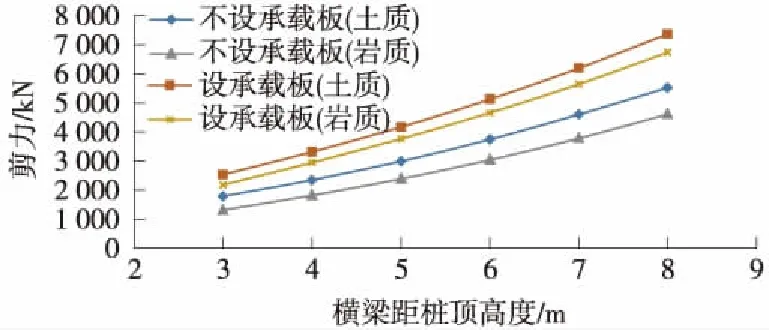
圖7 橫梁最大剪力與橫梁位置的關系曲線

主樁最大彎矩及剪力隨橫梁距樁頂長度呈先減小后增大的“V”字形變化，最大彎矩在橫梁距樁頂長度為4～5 m時最小，該處主樁橫梁上部與下部最大彎矩基本相等，剪力數值不大，不作為控制因素，因此，橫梁距樁頂長度為4～5 m時，主樁受力最優。在橫梁距樁頂長度小于6 m時，設置承載板能有效改善主樁受力；橫梁距樁頂長度大于6 m時，橫梁上設置承載板已幾乎不影響主樁受力。

橫梁最大彎矩、剪力隨橫梁距樁頂長度增大而增大，橫梁距樁頂長度小于6 m時橫梁最大彎矩變化不大，當橫梁距樁頂長度大于6 m時，橫梁彎矩顯著增大。橫梁剪力隨橫梁距樁頂長度變化呈線性增大趨勢，橫梁距樁頂長度對橫梁軸力影響不大。綜合分析橫梁彎矩、剪力及軸力，橫梁距樁頂長度宜小于6 m。對比相同地層設置承載板與不設置承載板橫梁受力，發現設置承載板后橫梁彎矩顯著減小，承載板的設置能有效改善橫梁的受力。

橫梁距樁頂長度小于6 m時副樁最大彎矩變化不大，當橫梁距樁頂長度大于6 m時，副樁彎矩顯著增大。橫梁位置對副樁軸力影響不大。對比相同地層設置承載板與不設置承載板副樁受力，發現設置承載板后副樁彎矩顯著減小，承載板的設置能有效改善副樁的受力。

綜合考慮主樁、橫梁及副樁的內力隨橫梁距樁頂長度變化規律，橫梁距樁頂長度為4～5 m，計算模型懸臂段長度為14 m，因此，橫梁位置距主樁樁頂最佳距離為0.30L～0.35L(L為主樁懸臂段長度)。在橫梁距樁頂長度小于6 m時，設置承載板能有效改善主樁受力；橫梁距樁頂長度大于6 m時，橫梁上設置承載板已幾乎不影響主樁受力；承載板的設置能有效降低橫梁及副樁的彎矩，同時有效改善副樁的軸力。綜合考慮主樁、橫梁、副樁的受力，橫梁設置位置不影響承載板對結構內力的改善效果。

3.3.2 橫向樁間距對結構的影響

分別建立錨固段為巖質及土質、主樁及副樁橫向間距為5～9 m的計算模型，分析計算各種情況下的受力情況，提取結構各部件的力學指標，對結構進行分析總結。代表性內力曲線如圖8～圖10所示。

圖8 主樁最大彎矩隨樁基橫向間距變化曲線

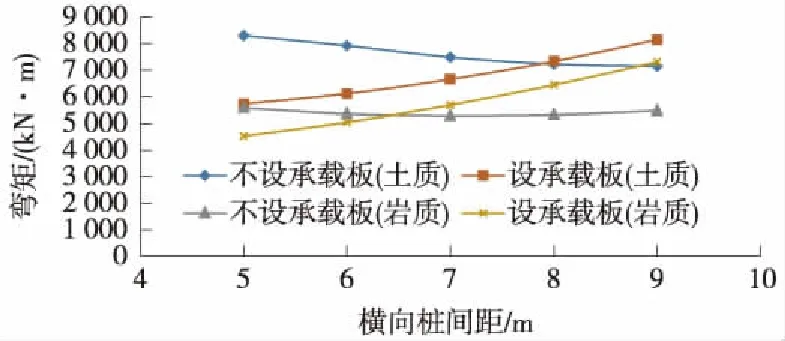
圖9 橫梁最大彎矩隨樁體橫向間距變化曲線

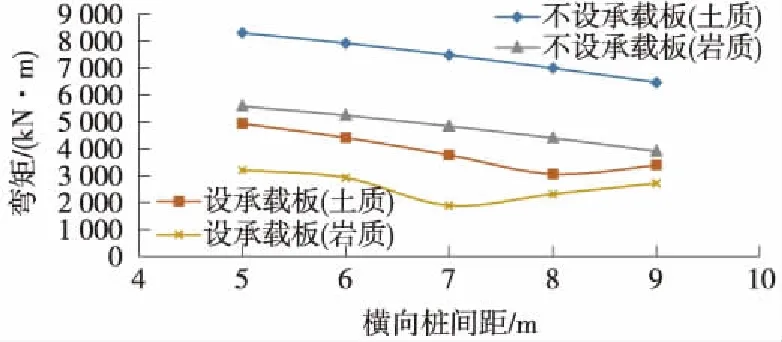
圖10 副樁最大彎矩隨樁體橫向間距變化曲線

(1)橫向樁間距變化對主樁內力的影響

橫向樁間距變化對主樁內力的影響，錨固段為巖質地層與土質地層變化規律一致，各拐點的數值有所差異，以巖質地層為例進行詳細分析。

主樁最大彎矩隨樁體橫向間距的增加呈現增大趨勢，當樁體橫向間距小于7 m時，主樁最大彎矩變化較小，當樁體橫向間距大于7 m，主樁最大彎矩隨著樁體橫向間距的增加而明顯增大。這是因為主樁最大正應力的發生位置不同造成的，當樁體橫向間距小于7 m時，最大彎矩發生在橫梁與主樁連接的部位，改變樁體橫向間距并不影響作用在主樁上的側向土壓力，因此，最大彎矩的值保持不變；當樁體橫向間距大于某一值時，由于作用在橫梁上的豎向應力增大，最大彎矩發生在樁體的錨固段。

對于不設置承載板結構，主樁最大剪力隨樁體橫向間距呈先減小后增大的趨勢，橫向樁間距為7 m時，剪力最小；對于設置承載板的結構，主樁最大剪力隨橫向樁間距增大而增大。

當橫向樁間距小于8 m時，不設置承載結構主樁最大彎矩大于設置承載板結構；當橫向樁間距大于8 m時，不設置承載板結構主樁最大彎矩小于設置承載板結構。說明當樁間距大于8 m時，由設置承載板增加的豎向力而產生的彎矩已經大于承載板卸荷作用減小的側壓力而產生的彎矩，因此，橫向樁間距大于8 m時，不宜橫梁上滿鋪設置承載板。

(2)橫向樁間距變化對橫梁內力的影響

橫向樁間距變化對橫梁內力的影響，錨固段為巖質地層與土質地層變化規律一致，各拐點的數值有所差異，以巖質地層為例進行詳細分析。

橫梁最大彎矩隨樁體橫向間距的增大呈現增大趨勢，設置承載板結構橫梁最大彎矩增大速度大于不設置承載板結構。當樁體橫向間距小于6.5 m時，設置承載板結構橫梁的最大彎矩小于不設置承載板的值，當樁體橫向間距大于6.5 m時，設置承載板結構橫梁的最大彎矩大于不設置承載板的值。

橫梁最大剪力隨樁體橫向間距的增加呈現增大趨勢，設置承載板時副樁最大剪力大于不設置承載板時的值。主要是因為設置承載板之后，樁體間的土壓力和上部列車、軌道荷載作用于樁體橫梁之上，致使最大剪力變大。

(3)橫向樁間距變化對副樁內力的影響

橫向樁間距變化對副樁內力的影響，錨固段為巖質地層與土質地層變化規律一致，各拐點的數值有所差異，以巖質地層為例進行詳細分析。

對于不設置承載板的結構，副樁最大彎矩隨樁體橫向間距的增加呈現減小趨勢；對于設置承載板的結構，副樁最大彎矩隨樁體橫向間距的增加呈現先減小后增大的趨勢，當樁體橫向間距超過某一值之后，設置承載板時副樁最大負彎矩將大于不設置承載板時的值。當橫向樁間距為7 m時，設置承載板結構的彎矩為最小值。

副樁最大剪力隨樁體橫向間距的增加呈現減小趨勢，設置承載板時副樁最大剪力小于不設置承載板時的值。主要是因為設置承載板之后，樁體間的土壓力和上部列車、軌道荷載作用于樁體橫梁之上，進而減小了樁體的側向壓力，致使最大剪力變小。

(4)橫向樁間距總結

綜合考慮主樁、橫梁及副樁的內力隨橫向樁間距的變化規律，設計建議如下。

①錨固段為巖質地層時，橫向樁凈間距宜為6～7 m；當橫向樁間距大于8 m時，不宜在橫梁上滿鋪設置承載板。

②錨固段為土質地層時，橫向樁凈間距宜為7～8 m；當橫向樁間距大于9 m時，不宜在橫梁上滿鋪設置承載板。

3.3.3 主樁錨固段長度對結構的影響

分別建立錨固段為巖質及土質、懸臂段長固為15 m、錨固長度為7～14 m的計算模型，分析計算各種情況下的受力，提取結構各部件的力學及變形指標，對結構進行分析總結。代表性內力曲線如圖11、圖12所示。

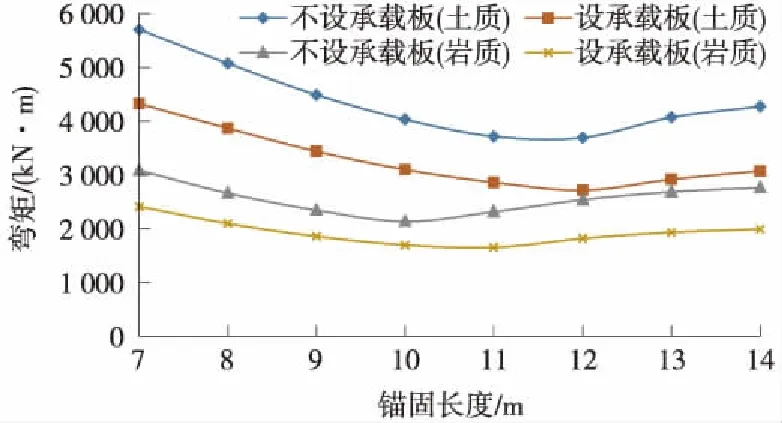
圖11 主樁最大彎矩隨主樁錨固段長度變化曲線

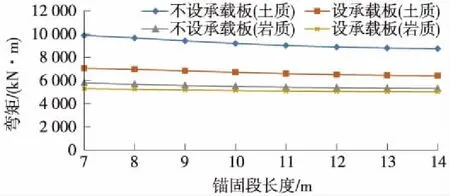
圖12 橫梁最大彎矩隨主樁錨固段長度變化曲線

主樁最大彎矩隨主樁錨固深度變化影響較大，各工況均呈現先減小后增大的趨勢。錨固段為土質地層，錨固段長度為12 m時，主樁彎矩最小；錨固段為巖質地層，錨固段長度為10 m時，主樁彎矩最小。主樁錨固深度對主樁剪力基本沒影響。設置承載板的內力均小于未設置承載板，說明錨固深度不影響承載板對結構內力的改善效果。主樁錨固深度對橫梁及副樁內力基本無影響。

主樁錨固深度設置合理能有效改善主樁的受力。錨固段為土質地層時，錨固段長度最佳為0.8L(L為主樁懸臂段)；錨固段為巖質地層時，錨固段長度最佳為2L/3。錨固深度不影響承載板對結構內力的改善效果。

4 結論

通過對h型樁板墻支擋結構設計關鍵參數影響分析，主要得出以下結論。

(1)橫梁布置距主樁樁頂的最佳距離為0.30L～0.35L。

(2)錨固段為巖質地層時，橫向最佳樁凈間距為6～7 m，主樁錨固段最佳長度約為2L/3。

(3)錨固段為土質地層時，橫向最佳樁凈間距為7～8 m，主樁錨固段最佳長度約為0.8L。

(4)橫梁設置位置及錨固深度不影響承載板對結構內力的改善效果，但橫向樁間距過大滿鋪設置承載板對結構不利。錨固段為巖質地層時，當橫向樁間距大于8 m時，不宜在橫梁上滿鋪設置承載板；錨固段為土質地層時，當橫向樁間距大于9 m時，不宜在橫梁上滿鋪設置承載板。