U形槽路堤立臂有限土體主動土壓力計算方法研究

汪 來,肖世國,2

(1.西南交通大學地質工程系,成都 610031； 2.西南交通大學高速鐵路線路工程教育部重點實驗室,成都 610031)

引言

U形槽路堤作為一種新型路基結構[1]，如圖1所示，一般具有占地面積小、整體剛度大、不均勻沉降小、防水性好等優點，適用于路堤放坡受限、地基較為軟弱、地下水豐富等地區。作用于U形槽立臂的土壓力是工程設計中的一個關鍵量值，目前常按經典土壓力理論計算[2-3]。由于經典土壓力理論建立在土體處于半無限狀態的基礎上，當U形槽路堤結構寬度較小時，其填土往往不符合半無限土體的假設，而是屬于有限土體。因此，在這種情況下按照經典土壓力理論計算并不一定合理。

圖1 U形槽路堤結構示意

目前，國內外學者對有限土體土壓力有一定的研究。Lawson和Yee[4]基于極限平衡理論分析了有限范圍的砂性土體土壓力系數，采用平面和雙線性滑移面兩種假定模式，結果顯示有限土體土壓力小于按照經典土壓力計算得到的主動土壓力，并且隨著有限土體寬度的增大而增大。Fan和Fang[5]采用有限元方法模擬了臨近傾斜基巖面剛性擋土墻上無黏性土主動土壓力的分布，并考慮了基巖面傾角、填土寬度等參數對土壓力分布的影響。結果表明：土壓力明顯小于庫倫土壓力，合力作用點也明顯高于1/3墻高。Greco[6]采用了狹窄寬度無黏性填土的多折線破壞模式，基于極限平衡法建立方程，推導出主動土壓力的表達式。高印立[7-8]基于土的塑性上限理論，給出一種有限土體土壓力的計算公式，并與朗肯土壓力的計算結果進行了對比，同時定義了有限土壓力影響系數并分析了不同因素對該系數的影響，并得到有限土體主動土壓力與朗肯主動土壓力大小關系不一定的結果，但該方法未考慮有限土體豎直滑面上的作用力。馬平等[9]基于極限平衡理論及平面滑裂面假定，在考慮土黏聚力及有限土體寬度的基礎上，推導并建立了有限土體破裂角與主動土壓力的計算公式，但該法仍未考慮有限土體豎直滑面上的作用力。王文杰等[10]指出若不考慮有限土體土壓力，則有可能導致結構不安全，但如果按照經典土壓力理論進行設計，則會造成比較大的浪費，并基于土壓力的基本原理，推導出了有限土體土壓力的計算方法。王洪亮等[11]在考慮有限土體豎直滑面上法向及切向力的基礎上，建立了求解有限土體主動土壓力的計算公式，并與有限元的結果進行了對比，但該方法將破裂角近似簡化為45°+φ/2(φ為土體內摩擦角)的假設并不一定符合實際。楊明輝等[12]通過試驗研究了3種擋墻變位模式下墻后砂性土體的破壞模式和土壓力分布，得到了有限土體主動土壓力小于庫倫土壓力的結果。李峰等[13]針對基坑工程中有限黏性土體的土壓力計算問題，基于滑楔體平衡理論，推導了考慮土體變形情況的有限土體土壓力計算模式，通過工程實例計算進行對比分析。結果表明：有限土體土壓力分布模式及其量值與半無限土體土壓力分布模式及其量值間存在顯著差異，當有限土體寬度不大于坑深的0.75倍時，宜按有限土體土壓力計算模式進行計算。王閆超等[14]基于平面滑裂的假設，采用薄層單元法推導了無黏性有限土體主動土壓力的解析解，并證明現行的經典土壓力公式為其特解。研究表明：有限土體主動土壓力在土體寬度較小時小于庫倫土壓力，當土體寬度增大時，有限土體土壓力逐漸增大，最終趨近于庫倫土壓力。廖俊展等[15]基于極限分析上限法推導了有限寬度條件下土壓力的計算模式，并與朗肯土壓力的計算進行了對比分析。結果表明：當土體寬高比小于0.7時，宜按有限寬度土體計算主動土壓力，同時得出了有限土體土壓力呈非線性分布且小于朗肯土壓力的結論。黃東[16]對臨近既有地下室的剛性擋土墻進行數值模擬，探討了填土高寬比、墻土摩擦角以及既有地下室深度對擋土墻土壓力的影響。馬繼才[17]針對地鐵車站基坑與鄰近構筑物間形成的有限土體，基于土體兩側相同深度處土壓力相等的假設，推導了有限土體土壓力的計算公式，提出了考慮土體黏聚力影響的有限土體臨界寬高比與臨界寬度修正模型，明確有限土體臨界寬高比主要介于0.55～0.65，并得到了基坑開挖深度越大，有限土體土壓力與經典土壓力之間的差異越明顯的結論。黃娟等[18]研究了填土寬度、黏聚力、內摩擦角和計算深度等對墻后有限寬度土體主動土壓力分布的影響。結果表明：有限土體土壓力隨土體黏聚力的增大而減小，隨土體內摩擦角和土體寬度的增大而增大。方燾等[19]通過有限土體自動控制模型試驗裝置，研究了不同變位模式下有限范圍的砂性土體的破裂面及土壓力分布，并與極限平衡理論計算結果進行了比較。肖昕迪等[20]通過建立不同寬度的離散元模型，得到了不同寬度土體的土壓力發展過程和極限狀態下主動土壓力的分布。研究表明：當土體寬度較小時，墻后有限土體土拱效應的疊加效應會影響主動土壓力分布，且當墻背粗糙時，有限土體寬度對主動土壓力影響較大，而當墻背光滑時，有限土體寬度幾乎不影響主動土壓力。

U形槽路堤結構屬于對稱結構，因此，其有限土體土壓力問題與前述的以往研究較多涉及的臨近既有建筑物或地下室的有限土體土壓力并不相同；同時，填土并非一定是無黏性土，其實際可能存在一定的黏性。有鑒于此，本文著眼于U形槽結構的具體受力特征，利用極限平衡理論，基于兩段折線型滑面假設，推導出一種計算U形槽有限土體土壓力的方法，可適于填土有一定黏性的情況，并根據U形槽立臂結構抗裂驗算控制條件，確定立臂底部截面擴大端的合理高度。

1 計算模型與分析推導

1.1 計算模型

由于U形槽路堤結構一般為正對稱結構，因此，在頂面對稱荷載與填土自重作用下，填土的中間對稱面上無切向力，對稱面兩側填土在極限狀態下受力模式如圖2所示(以右半側為例)。

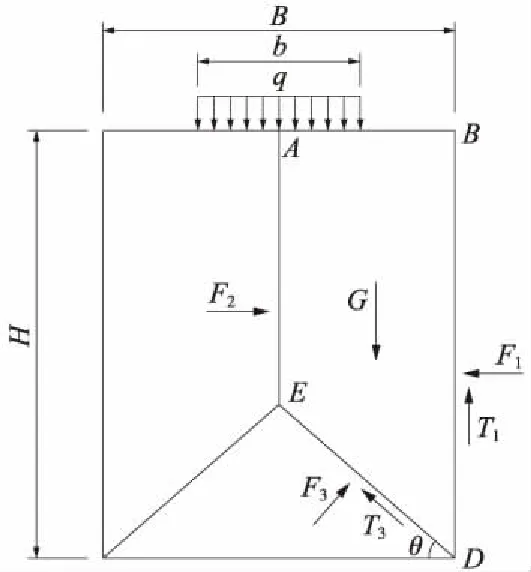
圖2 U形槽結構計算分析模型

由于填土擠壓U形槽立臂，使其產生側向變位，填土隨之產生側向位移，在填土達到主動極限狀態下，假設土體中形成AED折線型潛在滑面，其中DE面與水平向夾角為θ，潛在滑體在頂面荷載q與填土自重G的作用下，使得U形槽立臂BD上作用有側壓力F1與切向力T1，對稱面AE上作用有側壓力F2，滑面DE上作用有法向力F3與切向力T3。

1.2 平衡方程與土壓力求解

對潛在滑體ABDE，分別建立水平與豎直方向靜力平衡方程，得

F1+T3cosθ=F2+F3sinθ

(1)

T1+F3cosθ+T3sinθ=G+qb/2

(2)

式中，b為填土頂面荷載寬度；對土體采取Mohr-Coulomb強度準則，則T1=c0H+F1tanδ，T3=cB/(2cosθ)+F3tanφ，其中，c、φ分別為填土黏聚力與內摩擦角，c0、δ分別為填土與U形槽立臂界面的黏聚力與外摩擦角。

對于F1、F2、F3三個未知量，除式(1)、式(2)外，還需列力矩平衡方程。設F1、F2作用點距D點、E點高度與BD段、AE段高度比值分別為ma、mb(這里稱之為作用點系數，均為小于1的無量綱正數)，F3作用在DE段中點。于是，對D點合外力矩平衡，可得

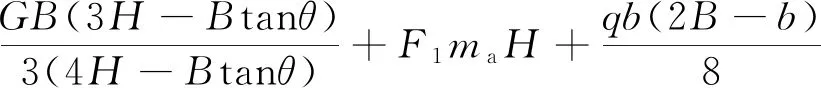
(3)

式中，G=(4γBH-γB2tanθ)/8，γ為填土重度，H、B分別為U形槽內部凈高和凈寬。聯立式(1)～式(3)可解得

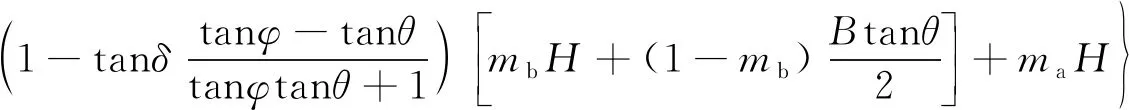
(4)

作用于立臂BD的土壓力合力Ea為

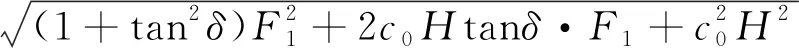
(5)

根據式(5)，由主動土壓力取極值的條件，即令dEa/dθ=0，利用Matlab的Solve函數即可求得θ，將符合條件的θ值代入式(5)，即可求得土壓力Ea之值。

2 實例分析

孟加拉帕德瑪大橋鐵路連接線一單線鐵路路堤工點擬采用U形槽結構設計方案，其填土重度γ=18.5 kN/m3，U形槽高度H=12 m，U形槽寬度B=7.2 m，填土內摩擦角φ=32°，黏聚力c=5 kPa，填土-立臂間外摩擦角δ=16°、界面黏聚力c0=2 kPa，頂面作用的對稱均布荷載q=68 kPa，作用寬度b=3.7 m，F1、F2的作用點分別取ma=1/3、mb=0.35。下面按前述方法分析該U形槽立臂上的土壓力。

2.1 主動土壓力

按照前述方法，計算得到立臂后側主動土壓力的結果如表1所示。為便于比較，表1同時也給出了已有文獻方法的計算結果。可見，本文方法計算的有限土壓力比文獻[7，11]方法分別約大23.4%、15.6%，本文方法相對偏保守。對于文獻[7]方法，計算有限土壓力時不考慮有限土體側面AE(對稱面)上的作用力，而文獻[11]則同時考慮其上的法向力與切向力，本文方法根據對稱性只考慮法向力。可見，對于AE面上作用力的不同處理會產生有差異的土壓力結果。同時，本文方法與文獻[7，11]方法所得土壓力均小于(分別約小13%，30%，25%)經典庫倫土壓力結果，說明此時采用半無限土體的土壓力算法是不合適的。此外，本文方法算得的破裂角小于文獻[7，11]及庫倫理論得到的結果，其相對誤差約在20%以內。

表1 不同方法計算結果對比

對于本例，本文方法計算得到主動土壓力及其相應破裂角隨U形槽寬度變化曲線如圖3所示。可見，隨著U形槽寬度的增大，立臂土壓力逐漸由有限土壓力轉變為半無限土體的土壓力。當B=7.5 m時，剛好為二者的分界點，同時，該點存在土壓力的極大值(見圖3(a)中P點)，即為庫倫土壓力；隨著B值繼續增大，土壓力逐漸減小，當達到12.5 m后(圖3(a)中Q點)，土壓力則保持不變。這是因為作用于頂面中心部位的條形外荷載q的影響所致，當B>12.5 m時，q對土壓力不再有影響。相應地，破裂角受q影響也呈現出隨B值的非線性變化特征(圖3(b))。

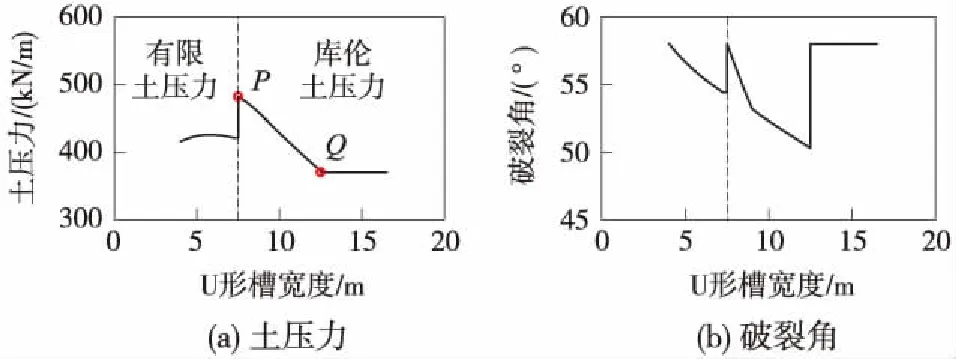
圖3 立臂土壓力及其破裂角隨U形槽寬度變化曲線

2.2 U形槽立臂厚度及合理形式

前已述及，按本文方法計算得U形槽立臂上的主動土壓力合力為Ea=421.9 kN/m。若按三角形土壓力分布模式，對立臂取單位寬度按懸臂梁進行計算，可得立臂底端彎矩為M=1.594×103kN·m。對立臂采用C35混凝土，受拉區配置12根φ28 mm、間距為55 mm的單排HRB335型縱向鋼筋。于是，可根據混凝土結構設計規范中規定的混凝土構件最大裂縫寬度計算公式進行立臂底端截面的抗裂計算。

圖4為根據鋼筋混凝土結構抗裂驗算及構造要求得到的距立臂底端不同高度處立臂最小厚度及裂縫寬度變化曲線。可見，立臂最小厚度隨高度呈逐漸收斂的折線型變化模式，兼顧施工方便，可對立臂內側在距其底端高2 m處向下呈45°角進行局部截面擴展，如圖5所示。

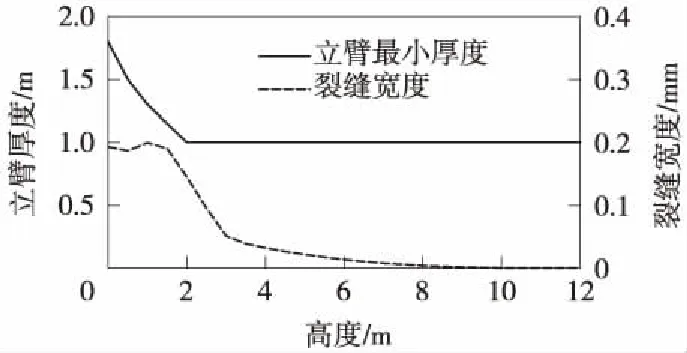
圖4 不同高度處的立臂最小厚度及裂縫寬度

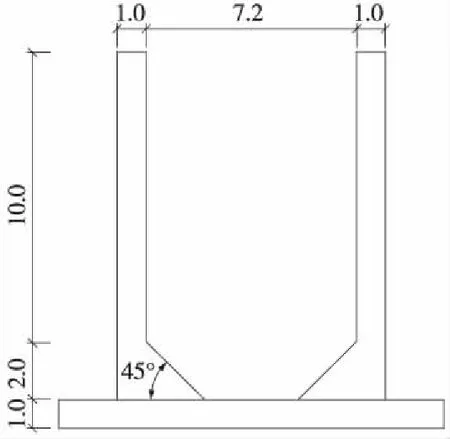
圖5 立臂的合理形式(單位：m)

3 參數影響分析

圖6 填土內摩擦角對主動土壓力及相應破裂角的影響曲線

由式(4)可知，填土內摩擦角、黏聚力與重度、填土-立臂界面外摩擦角與黏聚力、U形槽寬度與立臂高度、頂面外荷載等因素均對立臂后側主動土壓力有影響。因此，下面依托第2節所述實例，采用控制變量法，分別討論這些參數對該主動土壓力的影響。

3.1 填土內摩擦角

圖6為填土內摩擦角對有限主動土壓力及相應破裂角的影響曲線。可見，隨著土體內摩擦角φ的增大，土壓力Ea隨之呈非線性減小；本文方法計算結果大于文獻[7，11]；且隨著內摩擦角的增大，各方法所得土壓力逐漸趨于一致；破裂角θ則隨著內摩擦角的增大而增大，且本文方法計算結果小于相關文獻結果。

3.2 填土黏聚力

圖7為填土黏聚力對有限主動土壓力及相應破裂角的影響曲線。可見，隨著土體黏聚力c的增大，土壓力Ea隨之呈線性減小，破裂角θ則基本不變；填土黏聚力與土壓力之間近似呈線性關系，本文方法所得土壓力大于文獻[7，11]，其最大偏差在27%以內；對于不同黏聚力下的破裂角，本文方法與相關文獻方法相差在22%以內。

圖7 填土黏聚力對主動土壓力及相應破裂角的影響曲線

3.3 填土重度

圖8為填土重度對有限主動土壓力及相應破裂角的影響曲線。可見，隨著填土重度γ的增大，土壓力Ea隨之呈線性增大，而破裂角θ基本不變；填土重度與土壓力之間近似呈線性關系，本文方法所得土壓力、破裂角分別大于與小于相關文獻方法，其相差均在20%以內。

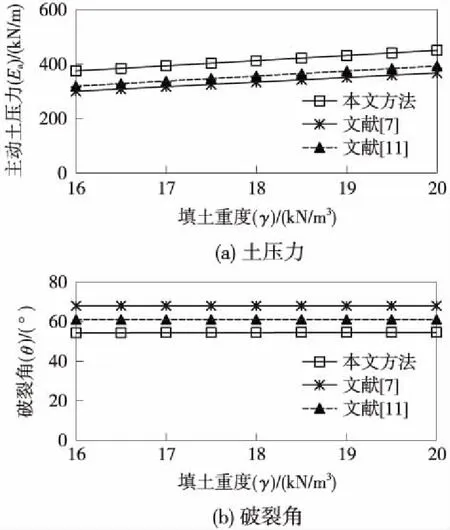
圖8 填土重度對主動土壓力及相應破裂角的影響曲線

3.4 填土-立臂界面外摩擦角

圖9為填土-立臂界面外摩擦角對有限主動土壓力及相應破裂角的影響曲線。可見，隨著外摩擦角δ的增大，土壓力Ea隨之呈非線性增大，且當外摩擦角小于10°時，土壓力基本不變，隨著外摩擦角的增大，各文獻方法得到的有限土壓力差距逐漸增大；破裂角θ隨外摩擦角的增大而逐漸減小，且其與外摩擦角之間近似呈線性關系；本文方法得到的土壓力、破裂角分別比既有文獻方法大26%、小23%。

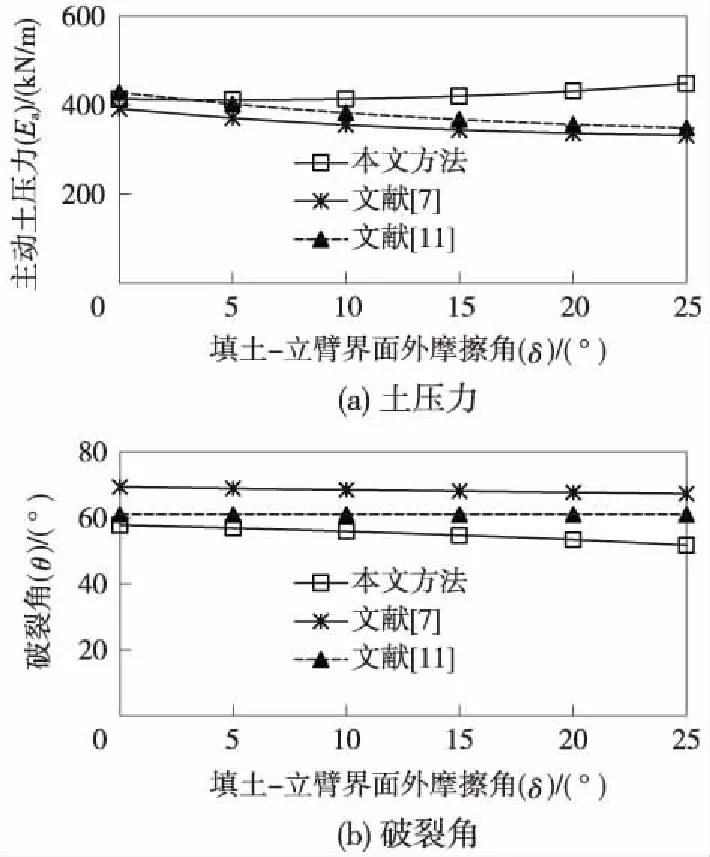
圖9 填土-立臂界面外摩擦角對主動土壓力及相應破裂角的影響曲線

3.5 填土-立臂界面黏聚力

圖10為填土-立臂界面黏聚力對有限主動土壓力及相應破裂角的影響曲線。可見，隨著填土-立臂界面黏聚力c0的增大，土壓力Ea隨之線性增大，而破裂角θ隨之略有減小；本文方法得到的土壓力、破裂角分別比既有文獻方法大23%、小19%。

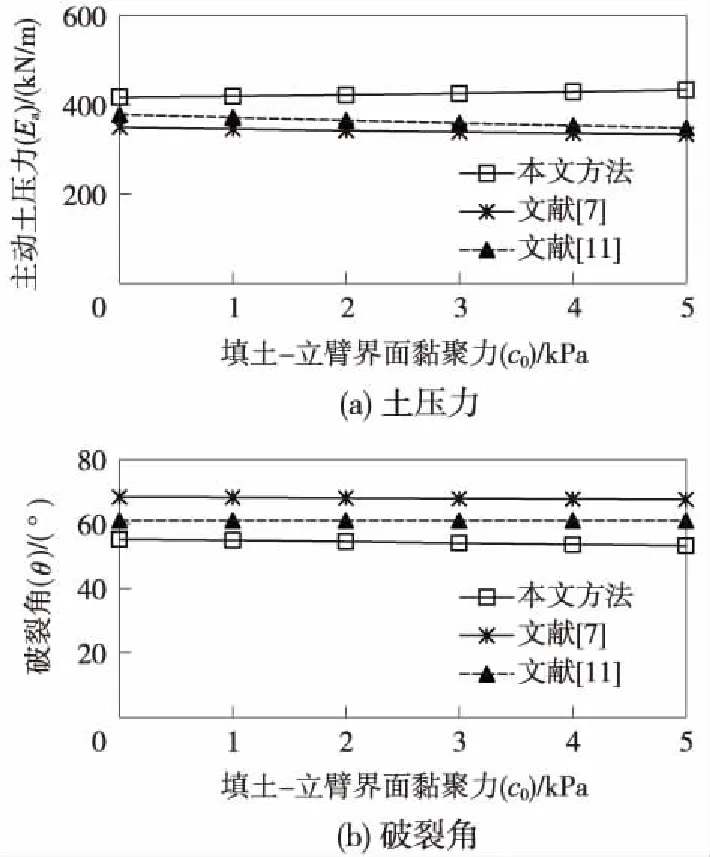
圖10 填土-立臂界面黏聚力對主動土壓力及相應破裂角的影響曲線

3.6 U形槽寬度

圖11為U形槽寬度對有限主動土壓力及相應破裂角的影響曲線。可見，隨著U形槽寬度B的增大，土壓力Ea隨之先略有增大后減小，而破裂角θ則隨之略有減小；且隨著U形槽寬度的增大，各方法所得土壓力相差逐漸減小，本文方法所得有限土壓力、破裂角分別比相關既有方法高31%、低22%。

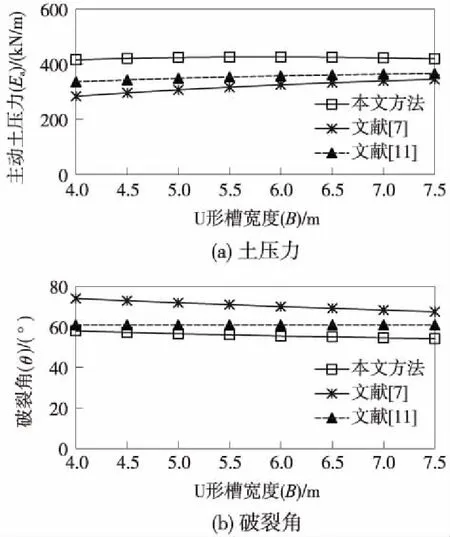
圖11 U形槽寬度對主動土壓力及相應破裂角的影響曲線

3.7 U形槽立臂高度

圖12為U形槽立臂高度對有限主動土壓力及相應破裂角的影響曲線。可見，隨著立臂高度H的增大，土壓力Ea隨之近似呈線性增大，而破裂角θ基本不變；隨著立臂高度的增大，本文方法所得土壓力與相關文獻方法所得結果相差逐漸增大；本文方法所得有限土壓力、破裂角分別比既有方法大25%、小19%。

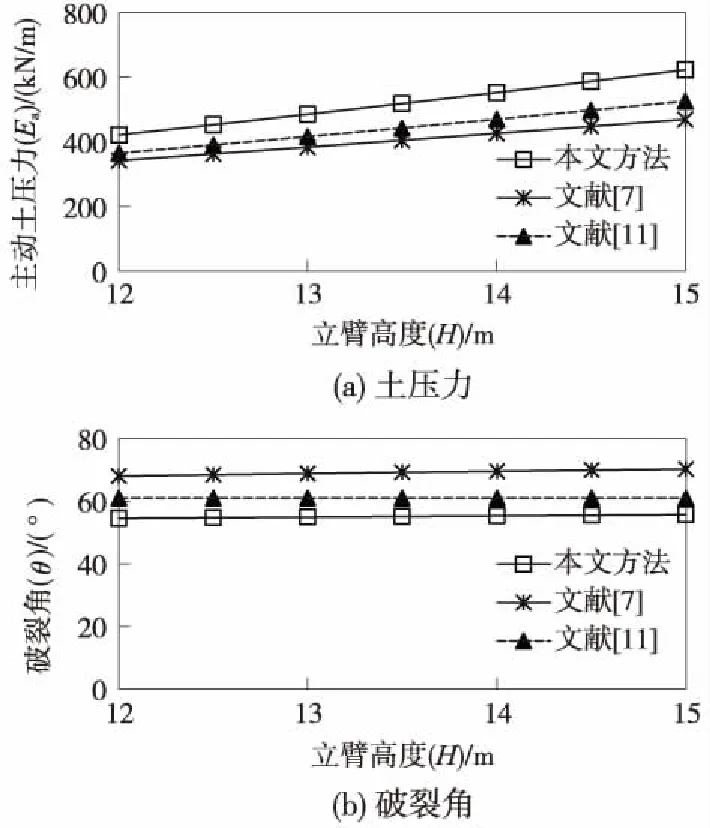
圖12 立臂高度對主動土壓力及相應破裂角的影響曲線

3.8 頂面外荷載

圖13為頂面外荷載對有限主動土壓力及相應破裂角的影響曲線。可見，隨著頂面外荷載q的增大，土壓力Ea隨之呈線性增大，而破裂角θ基本不變；頂面外荷載與土壓力之間近似呈線性關系，本文方法比既有文獻所得土壓力高出18%；頂面外荷載與破裂角之間關系也近似呈線性關系，且本文方法與比既有方法所得破裂角小19%。

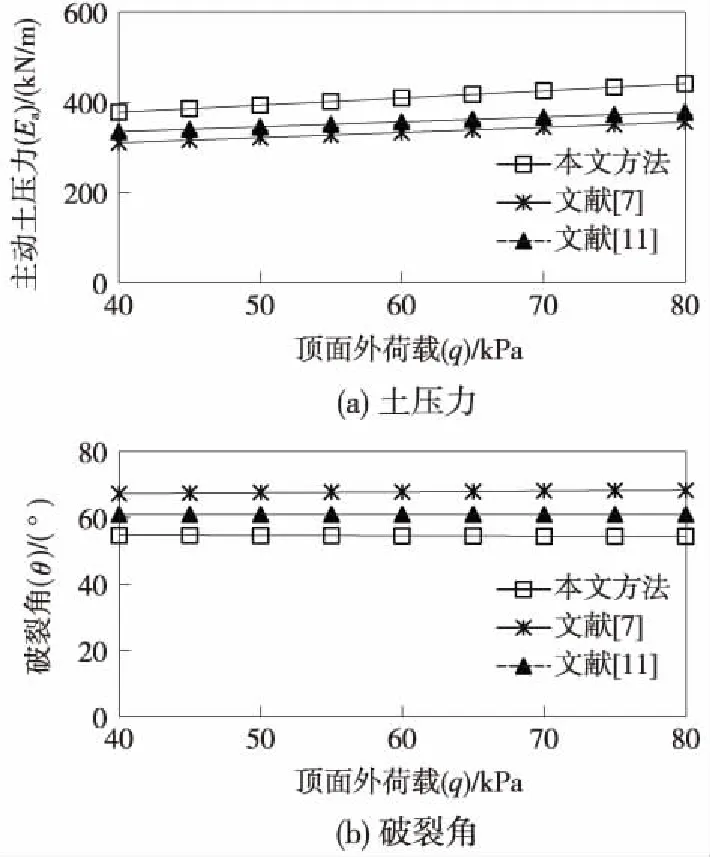
圖13 頂面外荷載對主動土壓力及相應破裂角的影響曲線

4 結論

基于兩段折線型滑面假設，采用極限平衡原理，給出了U形槽有限土體(包括黏性土)主動土壓力的計算方法并推導了相關公式，主要得出如下結論。

(1)根據U形槽路堤結構的對稱性，其豎向對稱面上只有水平力而無切向力，由此建立的主動土壓力分析模型，得到其土壓力大于完全不考慮對稱面上作用力與考慮對稱面上切向力及法向力確定的有限土壓力。

(2)當U形槽的寬高比相對較小時，應按有限土體計算其土壓力，反之，其土壓力等同于半無限土體土壓力；本文方法計算的有限土壓力小于半無限土體的庫倫主動土壓力，但明顯大于既有有限土壓力相關算法的結果。

(3)基于混凝土結構抗裂驗算可得到U形槽立臂不同高度處的最小厚度，實例分析表明，可采用立臂底端局部擴角為45°的變截面型式。

(4)填土重度、內摩擦角與黏聚力、填土-立臂界面外摩擦角與黏聚力、U形槽寬度與立臂高度、頂面外荷載等因素均對立臂后側有限主動土壓力有影響，其中填土內摩擦角、填土-立臂界面外摩擦角及U形槽寬度對土壓力均呈非線性影響。