大前進(jìn)比變轉(zhuǎn)速旋翼氣彈動(dòng)力學(xué)建模與載荷特性分析

余智豪， 周 云， 宋 彬

(中國直升機(jī)設(shè)計(jì)研究所 直升機(jī)旋翼動(dòng)力學(xué)重點(diǎn)實(shí)驗(yàn)室，江西 景德鎮(zhèn) 333001)

變轉(zhuǎn)速旋翼為當(dāng)前研究熱點(diǎn)，未來直升機(jī)發(fā)展中也有多處采用變轉(zhuǎn)速旋翼技術(shù)[1]。一方面降低旋翼轉(zhuǎn)速能有效提高旋翼升阻比，并能降低旋翼需用功率和耗油率[2-3]，從而達(dá)到提高航程的目的，波音公司采用優(yōu)化旋翼轉(zhuǎn)速概念(optimum speed rotor, OSR)[4]研制A160T[5-6]長航時(shí)無人直升機(jī)，創(chuàng)下續(xù)航時(shí)間、航程、降噪等多項(xiàng)記錄；另一方面，共軸高速直升機(jī)采用變轉(zhuǎn)速技術(shù)，通過降低旋翼轉(zhuǎn)速有效推遲前行激波產(chǎn)生，實(shí)現(xiàn)高速前飛，Sikorsky針對(duì)軍方“未來垂直起降飛行器”項(xiàng)目而研制的S-97侵襲者目前已突破370 km/h前飛速度。該構(gòu)型的高速直升機(jī)未來還有巨大的發(fā)展前景[7-8]。

隨著長航時(shí)直升機(jī)以及共軸高速直升機(jī)的研制成功和發(fā)展，越來越多的團(tuán)隊(duì)開展了變轉(zhuǎn)速旋翼方面的研究工作。雖然采用變轉(zhuǎn)速技術(shù)能提升直升機(jī)性能和提高前飛速度，但同時(shí)也出現(xiàn)復(fù)雜的氣彈動(dòng)力學(xué)問題。旋翼轉(zhuǎn)速降低和前飛速度增加使得反流區(qū)擴(kuò)大，該區(qū)域的槳葉段處于負(fù)迎角狀態(tài)，存在動(dòng)態(tài)失速以及負(fù)升力現(xiàn)象，這對(duì)反流區(qū)氣動(dòng)力計(jì)算提出更高要求。Chopra團(tuán)隊(duì)[9]在研究大反流區(qū)氣動(dòng)力計(jì)算時(shí)提出對(duì)動(dòng)態(tài)失速模型進(jìn)行修正，進(jìn)而提高計(jì)算精度。另有研究[10]表明通過修正L-B模型中的迎角以及變距運(yùn)動(dòng)，修正有效分離點(diǎn)和臨界法向力系數(shù)的方法能拓展模型適用范圍，在大反流區(qū)內(nèi)取得較好的氣動(dòng)力計(jì)算精度。另外大前進(jìn)比下反流區(qū)擴(kuò)大，氣動(dòng)載荷分布發(fā)生改變，國外團(tuán)隊(duì)在研究UH-60全尺寸變轉(zhuǎn)速試驗(yàn)[11]當(dāng)中發(fā)現(xiàn)：隨著反流區(qū)的擴(kuò)大，旋翼為滿足配平會(huì)造成槳葉內(nèi)外段氣動(dòng)載荷差距增大，同時(shí)反流區(qū)內(nèi)的負(fù)升力區(qū)域以及反流區(qū)內(nèi)氣動(dòng)中心位置的改變會(huì)造成槳葉內(nèi)外段的扭矩差異，使得槳葉產(chǎn)生周期性的脈沖氣動(dòng)載荷，同時(shí)對(duì)槳葉結(jié)構(gòu)載荷以及槳轂載荷都帶來嚴(yán)峻的影響。

旋翼轉(zhuǎn)速降低會(huì)導(dǎo)致槳葉頻率比增加，所以槳葉通常設(shè)計(jì)成剛硬輕質(zhì)，以提高揮舞擺振固有頻率，盡可能的使其在轉(zhuǎn)速區(qū)間內(nèi)出現(xiàn)較少的共振點(diǎn)。馬里蘭大學(xué)研究團(tuán)隊(duì)針對(duì)變轉(zhuǎn)速技術(shù)進(jìn)行多個(gè)轉(zhuǎn)速下的風(fēng)洞試驗(yàn)[12]，試驗(yàn)中前進(jìn)比最高達(dá)到1.2。試驗(yàn)表明：前進(jìn)比增加，揮舞載荷4/rev的諧波量顯著增加(4片槳葉)，同時(shí)槳轂垂直力4/rev的諧波量顯著增加，且扭矩會(huì)更早的受到尾跡干擾的影響。槳盤低馬赫數(shù)區(qū)和反流區(qū)擴(kuò)大后，槳根氣動(dòng)力矩在旋轉(zhuǎn)周期內(nèi)會(huì)產(chǎn)生很強(qiáng)的峰值變化。在轉(zhuǎn)速范圍內(nèi)，槳葉固有頻率與旋翼整數(shù)倍轉(zhuǎn)速頻率存在多個(gè)交叉點(diǎn)，會(huì)帶來嚴(yán)重的振動(dòng)載荷問題。國內(nèi)有關(guān)變轉(zhuǎn)速動(dòng)力學(xué)方面的研究較少，韓東等[13-14]針對(duì)變轉(zhuǎn)速旋翼動(dòng)力學(xué)問題進(jìn)行理論分析和模型旋翼實(shí)驗(yàn)，研究發(fā)現(xiàn)：轉(zhuǎn)速降低，揮舞、擺振低階載荷幅值增加，且在共振轉(zhuǎn)速狀態(tài)下?lián)]舞、擺振運(yùn)動(dòng)存在相互耦合，出現(xiàn)低階揮舞、擺振載荷突增的現(xiàn)象。目前國內(nèi)并未開展大前進(jìn)比旋翼氣彈動(dòng)力學(xué)相關(guān)的研究工作。

降低轉(zhuǎn)速會(huì)出現(xiàn)復(fù)雜的大前進(jìn)比旋翼氣彈動(dòng)力學(xué)問題，對(duì)變轉(zhuǎn)速旋翼設(shè)計(jì)提出了嚴(yán)格的要求。本文針對(duì)大前進(jìn)比變旋翼氣彈動(dòng)力學(xué)問題，建立考慮大前進(jìn)比配平的旋翼氣彈分析模型；并對(duì)大前進(jìn)比反流區(qū)氣動(dòng)力計(jì)算和配平計(jì)算進(jìn)行適當(dāng)修正，重點(diǎn)分析不同轉(zhuǎn)速狀態(tài)下的槳葉氣動(dòng)和結(jié)構(gòu)載荷，并得出相應(yīng)結(jié)論，為變轉(zhuǎn)速旋翼結(jié)構(gòu)設(shè)計(jì)以及后續(xù)的動(dòng)力學(xué)優(yōu)化設(shè)計(jì)提供理論依據(jù)。

1 大前進(jìn)比旋翼氣彈動(dòng)力學(xué)建模

1.1 旋翼動(dòng)力學(xué)模型

本文采用Green應(yīng)變以及中等變形理論，通過Hamilton原理建立旋翼動(dòng)力學(xué)方程

(1)

式中， δU為系統(tǒng)應(yīng)變能，其變分形式可表示為

(2)

式中：ε為應(yīng)變矩陣；σ為材料應(yīng)力矩陣。

δT為動(dòng)能項(xiàng)，表達(dá)式為

(3)

式中：qb為廣義自由度矩陣；Mb為槳葉慣性運(yùn)動(dòng)引起的質(zhì)量矩陣；FM為動(dòng)能的非線性廣義力。

δW為外載荷做功項(xiàng)，包括氣動(dòng)力和力矩兩部分

(4)

式中：Fa為氣動(dòng)力；Ma為氣動(dòng)力矩；Gb為廣義力系數(shù)矩陣。

采用中等變形梁理論以及有限元方法建立旋翼動(dòng)力學(xué)模型，并采用Newmark積分法建立氣彈響應(yīng)計(jì)算模型，通過計(jì)算得到槳葉上每個(gè)自由度節(jié)點(diǎn)的響應(yīng)，進(jìn)而求解槳葉剖面結(jié)構(gòu)載荷。槳葉剖面結(jié)構(gòu)載荷是由當(dāng)前剖面至槳尖的長度內(nèi)單位長度氣動(dòng)載荷和剖面單位長度慣性載荷積分而來，為

F=FI+FA

(5)

式中：F為廣義力； 下標(biāo)I為慣性載荷部分； 下標(biāo)A為氣動(dòng)載荷部分。槳葉載荷計(jì)算方法采用力積分法，表達(dá)式為

(6)

(7)

式中：L,M為剖面位置的三個(gè)力以及三個(gè)力矩，包括氣動(dòng)和結(jié)構(gòu)載荷兩個(gè)部分；f,m為整片槳葉的載荷量； 下標(biāo)u,v,w分別為徑向、弦向和垂直于弦向方向的位移。

1.2 大前進(jìn)比反流區(qū)氣動(dòng)力計(jì)算修正

本文采用的旋翼氣動(dòng)力計(jì)算模型為非線性準(zhǔn)定常氣動(dòng)模型。有效迎角采用小角度假設(shè)(見式(8))。但槳根段剖面ut速度小，有效迎角大，若繼續(xù)采用小角度假設(shè)會(huì)造成較大誤差；同時(shí)反流區(qū)槳葉剖面來流從翼型后緣向前緣移動(dòng)，又處于負(fù)迎角狀態(tài)。為準(zhǔn)確描述在槳葉剖面坐標(biāo)系內(nèi)合速度矢量方向變化導(dǎo)致的實(shí)際迎角變化，對(duì)有效迎角表達(dá)式進(jìn)行修正，修正后的表達(dá)式為

α=tan(-up/ut)≈-up/ut

(8)

式中：ut為剖面弦向速度；up為垂直于弦向速度。

(9)

XH-59A旋翼在μ=0.45的槳葉剖面迎角分布圖，如圖1所示。明顯看出在未修正前剖面有效迎角在270°附近階躍式跳動(dòng)且不是連續(xù)分布，偏離真實(shí)情況。說明此時(shí)小角度假設(shè)在低馬赫數(shù)區(qū)域以及反流區(qū)內(nèi)不適用。通過修正方法改進(jìn)之后，有效迎角呈連續(xù)變化且變化趨勢(shì)合理(在后行側(cè)低馬赫數(shù)區(qū)域迎角為負(fù))，這說明本文提出的方法有效可靠。

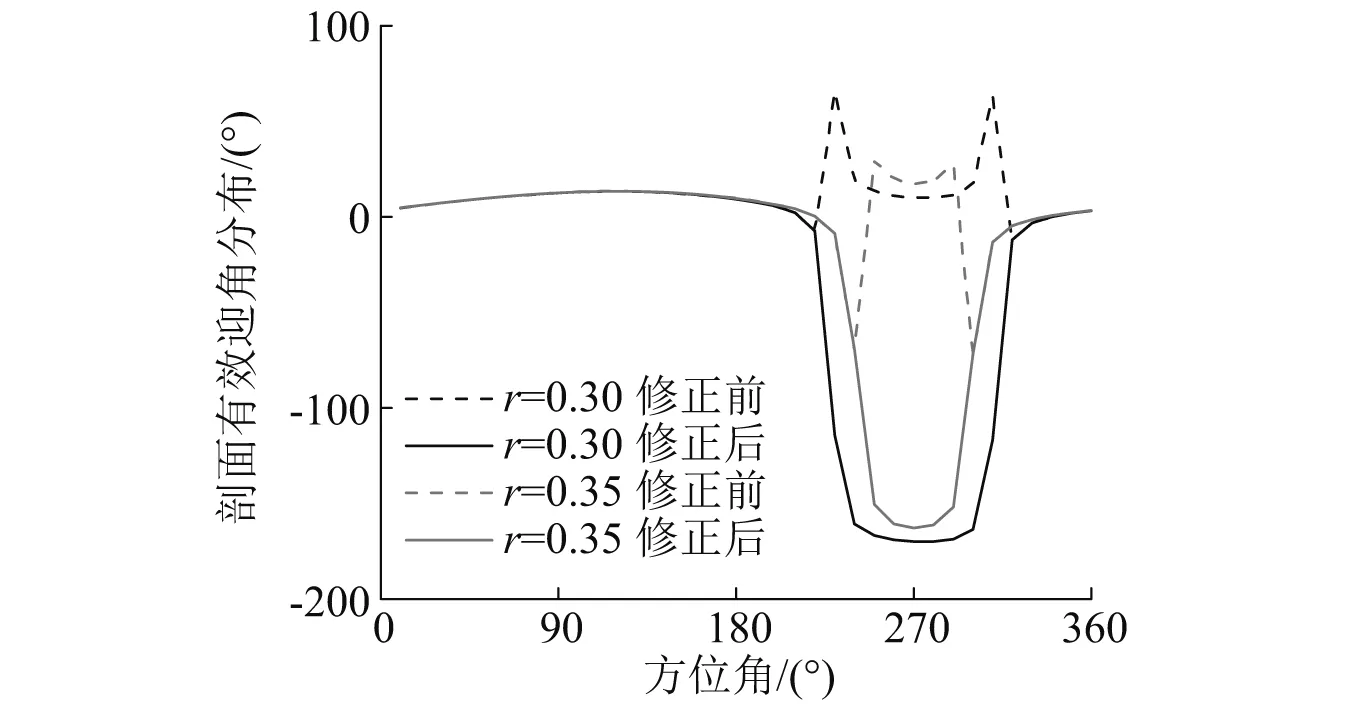
圖1 迎角修正Fig.1 The correction of angle of attack

1.3 大前進(jìn)旋翼氣彈配平計(jì)算修正

大前進(jìn)比旋翼氣彈分析中配平計(jì)算為關(guān)鍵環(huán)節(jié)之一。目前旋翼配平計(jì)算普遍采用Newton迭代法，傳統(tǒng)方法在中小前進(jìn)比條件下具有很好的收斂性，但配平計(jì)算中只生成一次Jacobian矩陣，且矩陣質(zhì)量與初始配平操縱有關(guān)。

隨著前進(jìn)比增加、氣流非對(duì)稱性增加、操縱量的變化對(duì)配平影響的敏感度增加，造成迭代計(jì)算量增加，配平計(jì)算難以收斂甚至發(fā)散。本文建立一種自適應(yīng)Newton迭代過程，如圖2所示。通過在迭代過程中判斷殘差數(shù)值變化情況，及時(shí)根據(jù)中間迭代的操縱值更新Jacobian矩陣，進(jìn)行新一輪的配平迭代，采用逐步逼近的方式控制殘差變化，從而能保持良好的收斂性，擴(kuò)展配平計(jì)算的適用范圍。

圖2 Newton迭代流程Fig.2 Newton iteration flow

1.4 模型驗(yàn)證

為驗(yàn)證本文旋翼動(dòng)力學(xué)模型的準(zhǔn)確性，本節(jié)采用XH-59A全尺寸風(fēng)洞試驗(yàn)計(jì)算的剛性槳葉模態(tài)頻率并對(duì)比驗(yàn)證。具體參數(shù)可在文獻(xiàn)[15]中查閱。本文計(jì)算的低階槳葉模態(tài)與試驗(yàn)值吻合度良好，如圖3所示。圖中：F1為揮舞1階；F2為揮舞2階；E1為擺振1階；E2為擺振2階；T1為扭轉(zhuǎn)1階。證明本文采用的旋翼動(dòng)力學(xué)模型準(zhǔn)確有效。

圖3 槳葉模態(tài)頻率Fig.3 Rotor blade dynamic modes

2 大前進(jìn)比旋翼氣彈動(dòng)力學(xué)特性分析

本文采用的OSR專利技術(shù)中有較詳細(xì)參數(shù)的旋翼作為算例模型，其采用NACA0012翼型，具體參數(shù)如表1所示。重點(diǎn)研究不同轉(zhuǎn)速和前進(jìn)比下的旋翼氣動(dòng)/動(dòng)力學(xué)變化。選取75%～100%轉(zhuǎn)速和3組前飛速度組合，如表2所示。包括槳葉模態(tài)的計(jì)算和單旋翼風(fēng)洞配平的計(jì)算。

表1 OSR旋翼參數(shù)Tab.1 Rotor parameter of OSR

2.1 槳葉氣動(dòng)載荷分析

0.25R槳葉剖面氣動(dòng)力計(jì)算結(jié)果圖，如圖4所示。隨著轉(zhuǎn)速變化的曲線，從法向氣動(dòng)力結(jié)果圖4中可知，由于轉(zhuǎn)速降低，為保持相同拉力水平前行側(cè)的升力增加以及后行側(cè)升力集中，造成大前進(jìn)比下槳根剖面法向力沿方位角分布出現(xiàn)較大波峰效果，產(chǎn)生周期性交變脈沖效應(yīng)。轉(zhuǎn)速越低，該現(xiàn)象就越明顯。并且從圖4中觀察到，150 km/h前飛速度下槳根在后行側(cè)區(qū)域法向力幾乎為0，前飛速度增加開始出現(xiàn)負(fù)法向力，即會(huì)產(chǎn)生負(fù)升力效應(yīng)。

圖4 半徑0.25R剖面法向力Fig.4 Normal force of 0.25R

半徑0.25R剖面力矩計(jì)算值結(jié)果圖，如圖5所示。圖5(a)中75%轉(zhuǎn)速下力矩在270°附近出現(xiàn)脈沖式跳動(dòng)(此時(shí)前進(jìn)比為0.295)。圖5(b)中，隨著前飛速度增加至200 km/h，力矩峰值更加明顯，脈沖式效應(yīng)更突出。最終大前進(jìn)比下槳根剖面產(chǎn)生周期性交變脈沖式氣動(dòng)力矩。旋翼后行側(cè)的升力集中和反流區(qū)的交變脈沖效應(yīng)都會(huì)對(duì)載荷造成影響。

圖5 半徑0.25R剖面氣動(dòng)力矩Fig.5 Aero moment force of 0.25R

2.2 槳葉結(jié)構(gòu)載荷分析

槳葉模態(tài)頻率的計(jì)算如圖6所示。從圖6可知，在75%～100%轉(zhuǎn)速區(qū)間，揮舞和擺振一階頻率未與轉(zhuǎn)速整數(shù)倍頻率發(fā)生交叉，這是為了避開共振問題，旋翼采用剛性槳葉將擺振1階頻率設(shè)置在1Ω以上。但揮舞2階在轉(zhuǎn)速區(qū)間內(nèi)與5Ω頻率發(fā)生交叉(旋翼為4片槳葉)，而5Ω頻率的載荷會(huì)傳遞至機(jī)身帶來振動(dòng)問題，同時(shí)也說明變轉(zhuǎn)速旋翼仍然存在共振問題，不容忽視。

圖6 槳葉模態(tài)頻率Fig.6 Rotor blade dynamic modes

旋翼在大前進(jìn)比下，剖面升力和力矩出現(xiàn)周期性脈沖效應(yīng)，同時(shí)轉(zhuǎn)速降低使得離心力剛度降低，造成揮舞載荷增大。計(jì)算槳根0.1R處揮舞和擺振彎矩并進(jìn)行諧波提取。在200 km/h速度下，揮舞彎矩呈現(xiàn)多個(gè)波峰，整體載荷水平隨轉(zhuǎn)速降低而不斷增加，載荷在270°附近波峰峰值明顯增加，曲線逐漸呈現(xiàn)2階諧波特征，說明揮舞2階諧波分量占比增加，如圖7(a)所示。圖7(b)揮舞諧波載荷分解圖也驗(yàn)證這一說法。轉(zhuǎn)速降低，揮舞0階、2階、3階載荷逐漸增加，而1階諧波量降低。這是因?yàn)殡x心力剛度降低而總拉力不變，導(dǎo)致?lián)]舞彎矩整體增加。而在配平計(jì)算中，隨這轉(zhuǎn)速降低，槳盤前傾角(αs)降低，導(dǎo)致1階諧波量降低。

圖7 槳根揮舞彎矩Fig.7 Flap bending moment of blade root

擺振彎矩計(jì)算結(jié)果圖，如圖8(a)所示。擺振運(yùn)動(dòng)受揮舞運(yùn)動(dòng)影響較大，受到氣動(dòng)力及擺振阻尼等影響。轉(zhuǎn)速降低，揮舞彎矩在90°和270°附近數(shù)值增加，相應(yīng)的擺振彎矩結(jié)果在90°和270°附近也出現(xiàn)較大波峰，且后行側(cè)升力集中以及反流區(qū)負(fù)升力對(duì)擺振載荷影響更加明顯。將擺振彎矩結(jié)果進(jìn)行諧波分解并提取前3階諧波，如圖8(b)所示。隨著轉(zhuǎn)速降低或前飛速度增加都會(huì)造成擺振各階諧波量增加，尤其對(duì)2階、3階載荷的影響最為顯著。

圖8 槳根擺振彎矩Fig.8 Edge bending moment of blade root

注意到揮舞和擺振彎矩2階諧波量在75%轉(zhuǎn)速時(shí)增幅較大，尤其是擺振彎矩，這一點(diǎn)可以從圖6模態(tài)頻率圖中觀察到：在75%旋翼轉(zhuǎn)速下?lián)]舞模態(tài)接近2Ω頻率，存在共振問題，擺振模態(tài)并未接近2Ω頻率，但揮舞也引起擺振載荷的增加，且2階影響顯著，若繼續(xù)降低轉(zhuǎn)速必然會(huì)引起強(qiáng)烈的2階擺振載荷，造成嚴(yán)重的動(dòng)力學(xué)問題。

2.3 脈沖氣動(dòng)力對(duì)結(jié)構(gòu)載荷的影響分析

為進(jìn)一步研究大前進(jìn)比狀態(tài)下的周期性交變脈沖氣動(dòng)力對(duì)結(jié)構(gòu)載荷的影響，計(jì)算85%轉(zhuǎn)速不同前進(jìn)比下的槳根0.1R剖面揮舞彎矩和揮舞彎矩中氣動(dòng)載荷部分(見式(7))，如圖9、圖10所示。從圖中看出隨著前進(jìn)比增加，揮舞彎矩中的氣動(dòng)部分出現(xiàn)多波峰。隨著前進(jìn)比增加，反流區(qū)擴(kuò)大即負(fù)升力區(qū)域增加，此時(shí)需要槳盤其他區(qū)域產(chǎn)生更多升力以抵消負(fù)升力，同時(shí)為滿足升力對(duì)稱性，后行側(cè)升力集中在槳葉外段，氣動(dòng)力造成的揮舞彎矩進(jìn)而增加。圖9中270°方位角后揮舞彎矩顯著增加也能驗(yàn)證這一點(diǎn)。

圖9 結(jié)構(gòu)載荷中氣動(dòng)載荷部分Fig 9 Part of airloads in structure loads

圖10 揮舞彎矩Fig.10 Flap bending moment

3 結(jié) 論

為研究大前進(jìn)比變轉(zhuǎn)速旋翼氣彈動(dòng)力學(xué)特性，本文修正大前進(jìn)比旋翼氣動(dòng)力計(jì)算方法和旋翼配平計(jì)算方法，建立了適用于大前進(jìn)比旋翼氣彈分析的模型，研究分析了不同轉(zhuǎn)速和速度下旋翼氣動(dòng)力和結(jié)構(gòu)載荷特性，并得到以下結(jié)論：

(1) 隨著前進(jìn)比增加，槳盤后行側(cè)出現(xiàn)升力集中，同時(shí)大反流區(qū)內(nèi)槳葉剖面幾乎不產(chǎn)生升力甚至出現(xiàn)負(fù)升力，氣動(dòng)力矩在大反流區(qū)內(nèi)出現(xiàn)較大波峰,升力及力矩呈現(xiàn)周期性脈沖效應(yīng)。

(2) 周期性脈沖氣動(dòng)力引起揮舞彎矩中氣動(dòng)力部分的增加，脈沖式氣動(dòng)力的影響隨著前進(jìn)比的增加更加顯著。

(3) 前進(jìn)比增加，導(dǎo)致?lián)]舞、擺振載荷增加，2階揮舞、擺振載荷增加明顯，且在轉(zhuǎn)速區(qū)間內(nèi)容易出現(xiàn)共振問題，惡化振動(dòng)載荷結(jié)果。