流冰對輸水隧洞襯砌的撞擊影響研究

貢 力， 王 鴻， 楊軼群， 王忠慧， 康春濤

(1. 蘭州交通大學 土木工程學院，蘭州 730070； 2. 蘭州交通大學 調水工程及輸水安全研究所，蘭州 730070)

我國西北地區冬季嚴寒，流冰期長且流冰量大，冰凌災害已成為西北地區輸水工程冰期安全運行面臨的首要問題[1]。然而位于此地區的輸水隧洞由于冬季氣候問題，經常受到水介質中流冰的撞擊作用，長期的碰撞則會造成隧洞襯砌疲勞累計損傷失效，縮短隧洞使用壽命。而對于在流冰與水工建筑物的撞擊方面，實地研究一般較難展開，因此數值模擬以及試驗驗證的方法在該研究領域內被廣泛的應用。

國內外學者對于流冰和水工建筑物以及海上結構碰撞方面進行了研究，Timco等[2]總結了所有與浮冰對結構影響相關的數據，用各種簡單的方法對沖擊進行了分析,發現沖擊力與浮冰在沖擊時的動能關系；趙緒新[3]對于空氣介質中流冰對于丁壩的撞擊破壞進行了數值模擬分析；張宿峰[4]對空氣介質下線彈性流冰模型對橋墩產生的撞擊壓力方面進行了研究；貢力等[5]對在空氣介質下線彈性流冰模型與輸水隧洞撞擊作用方面進行了相應的研究與分析；李明偉等[6]對冰荷載作用下護岸結構的撞擊影響進行了數值模擬分析；張健等[7]對水介質中船冰碰撞結構響應影響進行了數值模擬分析；黃焱等[8]對船-冰碰撞載荷時間歷程的模型試驗進行了研究與分析； Miryaha等[9]提出一種模擬浮冰對海洋結構影響的方法，討論了典型的浮冰作用模式和海上結構的壓力分布。綜上所述，國內外的學者對空氣介質下流冰與橋墩和海上結構撞擊研究較多，但針對水介質作用下流冰與寒旱地區輸水隧洞襯砌的撞擊作用研究較少。

因此，為了正確模擬碰撞過程中流冰-水-隧洞襯砌三者的相互作用，理清水介質對流冰-隧洞襯砌碰撞結構響應的影響，還原更加真實的碰撞場景，本文采用數值模擬結合試驗驗證的方法，運用LS-DYNA有限元軟件及室內物理模型試驗完成水介質中流冰與隧洞撞擊的研究與分析，探究不同碰撞工況下流冰對隧洞襯砌撞擊的力學性能規律，為西北寒旱地區冰期輸水安全提供支持。

1 流冰-隧洞碰撞有限元模型建立

1.1 流固耦合

在流冰與輸水隧洞襯砌接觸之前的近場逼近過程中，流冰與隧洞襯砌之間的水由于受到擠壓而預先產生一個高壓力場，這是一個不可忽略的重要因素，該壓力場使流冰與隧洞襯砌之間產生一個降低碰撞速度的“水墊效應”，對流冰碰撞起到緩沖作用。因此流冰與結構物的碰撞過程中周圍水的影響通過定義流固耦合來解決，流冰與隧洞襯砌采用拉格朗日網格，水介質與空氣介質采用歐拉網格，定義流固耦合關系可實現拉格朗日網格與歐拉網格相互作用，相互作用力通過耦合面進行轉換與傳遞。耦合面是一個正體積的封閉面，且至少與一個歐拉單元相交。

1.2 碰撞模型建立

水介質中流冰與隧洞襯砌相互作用是一種比較復雜的非線性動態響應過程，本文在不影響仿真結果的基礎上，對碰撞模型進行適當的簡化。選取西北寒旱地區“引大入秦”工程盤道嶺37#隧洞作為研究對象，利用 ANSYS 軟件建立水介質中隧洞和流冰的碰撞模型，并結合非線性有限元軟件 LS-DYNA 進行計算分析。隧洞襯砌混凝土材料模型采用美國聯邦高速公路管理局( FHWA) 開發的CSCM-CONCRETE模型, 該模型是美國聯邦高速公路管理局開發用來分析路邊防護欄與汽車撞擊性能的。該模型主要考慮了材料的硬化、率相關性以及損傷等，目前在混凝土材料低速沖擊方面應用廣泛[10]。具體材料參數如表1所示。

表1 混凝土材料模型參數Tab.1 Concrete material model parameters

對于冰材料而言，由于冰材料具有一定的復雜性，諸多學者在采用LS-DYNA軟件進行流冰與水工建筑物方面的碰撞模擬時，選取了LS-DYNA材料庫中的不同材料模型，包括各向同性彈性材料、各向同性彈性斷裂材料、可壓縮性泡沫材料等[11]。本文所采用的流冰材料參考了楊亮等[12]的研究數據，基于流冰碰撞時產生的破碎情況，選取了含有破碎效果的各向同性彈塑性斷裂材料作為此次數值模擬的流冰材料模型。流冰材料模型的參數如表2所示。

表2 冰材料模型參數Tab.2 Ice material model parameters

水介質與空氣介質材料均選取空白材料，而在狀態方程方面有區別是水介質采用的是Gruneisen狀態方程描述,空氣介質則采用的是線性多項式Polynomial狀態方程來描述。具體參數如表3～表5所示。

表3 水介質與空氣介質材料模型參數Tab.3 Water and air material model parameters

表4 水介質狀態方程參數Tab.4 Water medium state equation parameters

表5 空氣介質狀態方程參數Tab.5 Air medium state equation parameters

設置材料屬性后，對碰撞模型進行建立，建立的水介質中流冰與隧洞襯砌的碰撞模型如圖1所示。

圖1 水介質中流冰與隧洞襯砌碰撞模型圖Fig.1 Model of collision between flow ice and tunnel lining in water medium

圖中1為隧洞模型，因為考慮到碰撞作用以及計算時間的問題，選取對稱隧洞的一半模型用來求解分析，2為空氣域，3為水域模型。根據譚忠華[13]的研究發現，流體計算域大小對計算結果影響很小，考慮到流固耦合計算時間會大幅度增加，為節約計算資源，盡量接近真實碰撞情形，本文選取4.00 m×2.10 m×0.75 m的空氣域模型和4.00 m×2.10 m×2.25 m的水域模型，4為處于空氣域和水域中的流冰模型,該碰撞模型中流冰模型尺寸為0.5 m×0.5 m×0.2 m，其中流冰厚度為0.2 m。

空氣域未選擇全域而選取厚度為0.75 m的一層進行計算分析是因為通過觀察自然界流冰，漂浮的流冰大部分是浸泡在水介質中的，只有很小一部分處于空氣介質中，而本文研究的是中小型的流冰對輸水隧洞的碰撞影響，因此空氣域對流冰的影響較小，又基于本文采用流固耦合法進行計算分析，如果歐拉網格過多，則會造成流固耦合計算時間的大大增加。因此本文在保證碰撞結果精確性的條件下選取大約4倍流冰厚度的空氣域進行整個模型的計算分析。

1.3 邊界條件及初始條件

本文將隧洞襯砌底板及邊壁進行全約束，漂浮在水面的流冰處于豎向平衡狀態，所以在仿真模擬時忽略流冰所受的豎向荷載，只考慮水流拖動流冰運動的水平荷載，其水平荷載主要通過流冰的初速度體現，因此只對水介質中流冰施加撞擊方向的初速度[14]。流固耦合模型中還需定義歐拉單元的邊界條件和初始狀態。水域單元的邊界條件是隧洞底板，定義為剛性邊界條件，其余部分定義為自由出流邊界。空氣域單元的邊界條件是隧洞邊壁，但本文在建立空氣域模型時選擇建立0.75 m厚的一層空氣域而非全域進行模擬，所以空氣域與隧洞邊壁接觸的單元定義為剛性邊界條件，其余單元均定義為自由出流邊界。

2 碰撞工況選取

引大入秦工程盤道嶺37# 隧洞位于中國甘肅省永登縣，全長 15.723 km，設計流量32 m3/s，加大流量36 m3/s，設計水深為2.92 m，加大水深為3.37 m，縱坡 1/1 000。該隧洞的結構為反拱底板式斷面以及圓拱直墻形結構，隧洞的凈高為4.40 m，凈寬為4.20 m，半圓形拱頂，其半徑為2.10 m[15]。為研究水介質中不同工況下流冰與隧洞襯砌撞擊產生的影響以及分析流冰-水-空氣-隧洞襯砌四者耦合作用下隧洞襯砌的結構響應問題，本文選取附連水域與空氣域的流冰-隧洞襯砌碰撞模型，建立隨溫度變化的不同流冰壓縮強度和流冰厚度與隧洞襯砌的碰撞模型，使不同壓縮強度和厚度工況流冰以 3.0 m/s初速度撞擊隧洞襯砌。圖2為碰撞模型網格劃分圖，為了精確計算結果，隧洞網格采用分區劃分的原則，對隧洞受碰撞區網格進行加密處理[16]。

圖2 水介質中流冰與隧洞襯砌碰撞模型網格圖Fig.2 Mesh diagram of collision model between flow ice and tunnel lining in water medium

2.1 不同流冰壓縮強度工況選取

流冰壓縮強度會隨著溫度產生變化，參照王慶凱等[17]對黃河冰單軸壓縮強度的試驗與影響分析，溫度與流冰壓縮強度呈現出對數函數的關系，關系式為

σmax,h=0.767ln(|T|)+0.591,r=0.948

(1)

式中，σmax,h為平行冰面方向加載試樣極值壓縮強度， MPa；T為溫度，℃。

根據天堂水文站實測降水和部分蒸發資料以及鄰近氣象站資料推得冬季平均氣溫在-5℃左右，極端最低氣溫為-28.3 ℃。本文基于以上資料，對-5～-30 ℃溫度區間的流冰壓縮強度進行選取，通過不同溫度來控制流冰壓縮強度，在其他參數確定的情況下只改變流冰壓縮強度，利用1.2節所建立的碰撞模型，探究水介質中不同壓縮強度流冰對隧洞襯砌撞擊的作用，根據式(1)選取流冰壓縮強度工況如表6所示。

表6 流冰壓縮強度工況數據表Tab.6 Data sheet of flow ice compression strength condition

2.2 不同流冰厚度工況選取

通過觀察自然界中輸水工程流冰大多數屬于形狀不規則的板類結構，流冰厚度與當地氣候條件密切相關，本文綜合考慮到大通河冰情和盤道嶺隧洞所處地理位置以及參照徐國賓等[18-19]在流冰方面的研究，選取6 cm，10 cm，13 cm，16 cm，18 cm，20 cm厚度流冰，利用1.2節所建立的碰撞模型，探究水介質中不同厚度流冰對隧洞襯砌撞擊的影響作用。

3 不同碰撞工況隧洞襯砌動態響應分析

3.1 不同流冰壓縮強度

經過水介質中不同壓縮強度流冰對隧洞襯砌的撞擊模擬分析可以發現，對于小塊低速流冰撞擊隧洞襯砌時，形成的撞擊壓力相對較小，且流冰不會呈現出大面積破碎情況，當設置流冰的屈服應力為1.825 MPa時，隧洞襯砌的應力云圖及X方向位移云圖如圖3、圖4所示。

圖3 隧洞襯砌最大應力云圖Fig.3 Maximum stress cloud image of tunnel lining

圖4 隧洞襯砌最大X方向位移云圖Fig.4 Maximum X-displacement cloud image of tunnel lining

由圖3、圖4可知，隧洞襯砌所受的撞擊壓力在0.006 9 s時達到最大峰值，壓力最大峰值為1.29 MPa，且隧洞襯砌撞擊區的X方向位移也在該時刻達到最大峰值，位移峰值為2.62×10-5m。在其余壓縮強度工況下，撞擊壓力最大峰值分別為1.42 MPa，1.57 MPa，1.62 MPa，1.67 MPa，1.71 MPa，1.95 MPa，1.91 MPa，1.93 MPa，1.93 MPa，1.93 MPa；隧洞受撞擊區X方向位移最大峰值分別為2.73×10-5m，2.79×10-5m，3.00×10-5m，3.08×10-5m，3.05×10-5m，2.98×10-5m，3.05×10-5m，3.12×10-5m，3.14×10-5m，3.10×10-5m；對不同流冰壓縮強度工況下隧洞襯砌所受撞擊壓力以及X方向位移時程曲線進行匯總，如圖5、圖6所示。

圖5 不同壓縮強度流冰撞擊壓力時程曲線Fig.5 Time history curves of ice flow impacting pressure at different compression strengths

圖6 不同壓縮強度流冰下隧洞X方向位移時程曲線Fig.6 Time-history curve of X-displacement in the tunnel under ice different compression strengths

由圖5、圖6可知，不同流冰壓縮強度工況的壓力時程曲線以及隧洞受撞擊區X方向位移時程曲線均在同一時刻出現最大峰值且出現多峰值的情況，這是因為水介質中流冰與隧洞襯砌的碰撞過程屬于動態響應的過程，第一峰值為流冰在撞向隧洞襯砌的過程中，當其逼近隧洞襯砌時流冰與隧洞襯砌之間的水會形成一個高壓力場對隧洞襯砌產生作用，但作用較小，對隧洞襯砌產生的位移不明顯。隨后的第二個峰值為流冰撞擊到隧洞襯砌的作用峰值，此時為整個碰撞過程中的最大峰值，隧洞襯砌受撞擊區的位移在此時也達到最大值，由于本文在仿真模擬是采用的混凝土模型為CSCM混凝土模型，該模型在撞擊后會記錄混凝土的損傷變形。由圖6可知，隧洞襯砌混凝土在受到流冰撞擊時，會產生較大的變形，這部分變形包括彈性變形以及損傷變形，在撞擊過程發生后，隧洞襯砌的位移由最大峰值下降到穩定的損傷變形，由圖6可知隧洞襯砌發生的損傷變形在不同流冰壓縮強度工況下均穩定在1×10-5m左右。而對于壓力時程曲線的后續幾個峰值可以看成是由于撞擊過程中產生的波浪對隧洞襯砌的影響，這些峰值較小，對隧洞襯砌影響較小，因此本文不做討論。

3.2 不同流冰厚度

經過水介質中不同厚度流冰對隧洞襯砌的撞擊作用模擬分析可以發現，對于厚度較小速度較低的流冰撞擊隧洞襯砌，形成的撞擊壓力和變形相對較小，且流冰不會呈現出大面積破碎情況，當設置流冰的厚度為6 cm時，隧洞襯砌的應力云圖及X方向位移云圖如圖7、圖8所示。

圖7 隧洞襯砌最大壓力云圖Fig.7 Maximum stress cloud image of tunnel lining

圖8 隧洞襯砌最大X方向位移云圖Fig.8 Maximum X-displacement cloud image of tunnel lining

由圖7、圖8可知，當流冰厚度為5 cm時，達到撞擊壓力最大峰值的時間為0.008 49 s，撞擊壓力最大峰值為1.68 MPa，且隧洞襯砌受撞擊區的X方向位移也在該時刻達到最大峰值，位移最大峰值為1.62×10-5m。在其余厚度工況下，壓力最大峰值分別為2.02 MPa，2.15 MPa，2.20 MPa，2.10 MPa，2.06 MPa；位移最大峰值分別為3.24×10-5m，3.32×10-5m，3.40×10-5m，3.17×10-5m，3.26×10-5m；對不同流冰厚度工況下隧洞襯砌所受壓力以及位移時程曲線進行匯總，如圖9、圖10所示。

由圖9、圖10可知，不同厚度流冰工況的撞擊壓力時程曲線以及位移時程曲線也均出現多峰值的情況，原因與3.1節分析原因相同。而與圖6不同的是，在圖9中撞擊壓力的第一峰值是同時發生的，這是因為“水墊效應”產生，而第二峰值卻出現錯位的情況，這是由于不同厚度流冰在水介質中撞擊隧洞襯砌的過程中，由于流冰厚度增加，相應的碰撞面積也增加，水介質對流冰的阻力也增大，進而造成流冰與隧洞襯砌接觸時間上存在著時間差，所以造成第二峰值出現不同時刻的情況，位移時程曲線峰值也出現不同時刻的情況。由圖10可知，隧洞襯砌混凝土在受到流冰撞擊時，產生變形情況與3.1節分析一致，但是在撞擊過程發生后，不同厚度流冰工況下隧洞襯砌的損傷變形卻是均穩定在0～1×10-5m左右。

圖9 不同厚度流冰撞擊壓力時程曲線Fig.9 Pressure time-history curves of ice flow with different thickness

圖10 不同厚度流冰下隧洞X方向位移時程曲線Fig.10 Time-history curve of X-displacement in the tunnel under ice flow with different thickness

4 不同碰撞工況下最大峰值結果分析

4.1 不同壓縮強度流冰最大峰值分析

對圖5、圖6中時程曲線的最大峰值進行統計后，繪制不同壓縮強度流冰工況下隧洞所受的撞擊壓力峰值散點圖和X方向位移峰值散點圖，并進行曲線擬合。如圖11、圖12所示。

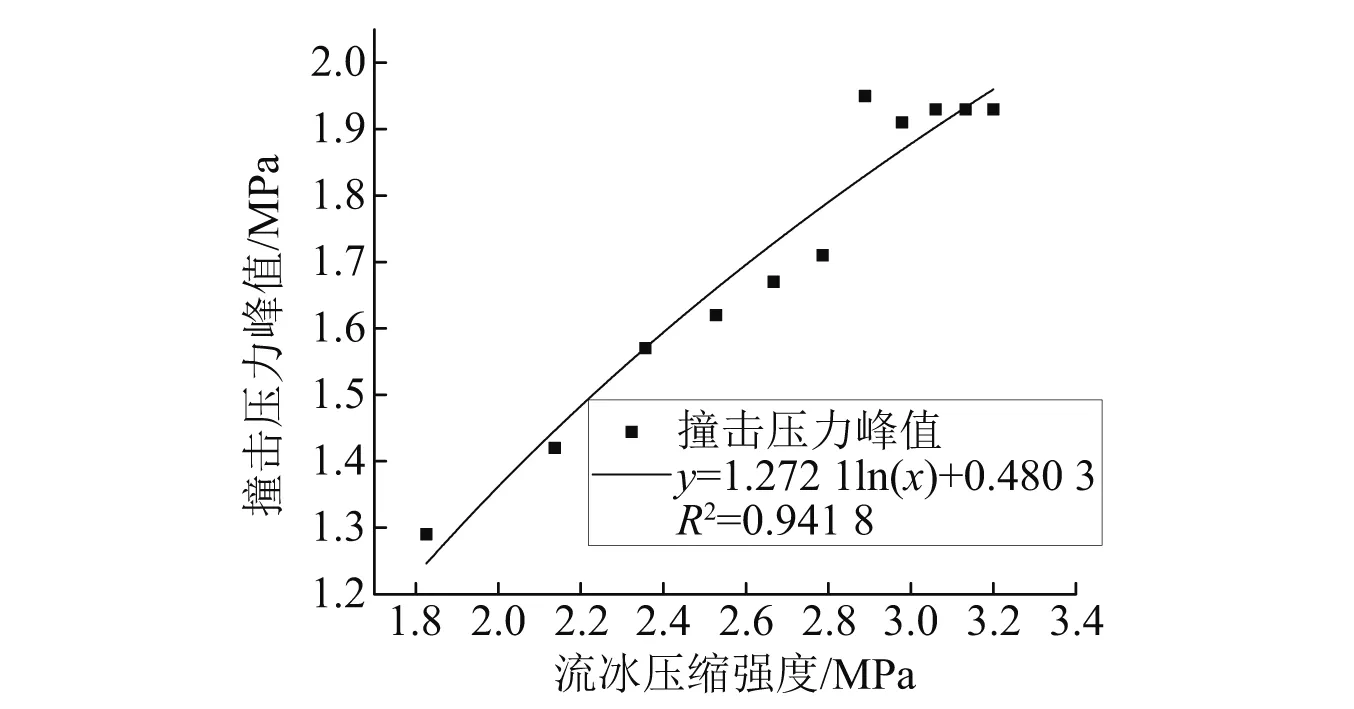
圖11 不同流冰壓縮強度撞擊壓力峰值圖Fig.11 Peak impact pressure of different ice compression strengths

圖12 不同流冰壓縮強度下隧洞X方向位移峰值圖Fig.12 Peak X-displacement in the tunnel under different ice compression strengths

由圖11、圖12可知，流冰壓縮強度與撞擊壓力和隧洞撞擊區X方向位移均呈現出對數函數的關系，由于水介質、空氣介質以及混凝土材料的影響，隧洞撞擊區位移的部分點出現偏移的情況，但就整體來說流冰壓縮強度與撞擊壓力和隧洞撞擊區X方向位移還是均呈現出對數函數的關系。

(1) 流冰壓縮強度與撞擊壓力的關系式為

y=1.272ln(x)+0.480 3

(2)

式中：y為撞擊壓力，MPa；x為流冰壓縮強度， MPa； 相關系數為R2=0.941 8。

(2) 流冰壓縮強度與隧洞襯砌受撞擊區的X方向位移關系式為

y=(9×10-6)ln(x)+(2×10-5)

(3)

式中：y為隧洞襯砌碰撞區X方向位移，m；x為流冰壓縮強度，MPa； 相關系數為R2=0.896 6。

不同流冰壓縮強度對應的隧洞襯砌受撞擊區X方向位移峰值擬合曲線相關系數略低，除了空氣介質、水介質以及混凝土材料的影響外，還有位移本身的限制條件。因為本文研究小塊流冰對于隧洞襯砌的撞擊影響，隧洞襯砌撞擊區的位移本來就是很微小，所以輸出位移會存在一定的誤差，導致擬合曲線的相關度略低。

4.2 不同厚度流冰最大峰值分析

對圖9、圖10中時程曲線的最大峰值進行統計后，繪制不同厚度流冰工況下隧洞所受撞擊壓力峰值散點圖和X方向位移峰值散點圖，并進行曲線擬合。如圖13、圖14所示。

圖13 不同厚度流冰撞擊壓力峰值圖Fig.13 Peak pressure of ice impingement with different thickness

圖14 不同厚度流冰下隧洞X方向位移峰值圖Fig.14 Peak X-displacement in the tunnel under different ice thickness

由圖13、圖14可知，流冰厚度與撞擊壓力和隧洞襯砌撞擊區位移均呈現出多項式函數的關系，同樣由于水介質、空氣介質以及混凝土材料的影響，隧洞撞擊區位移的部分點出現偏移的情況，但就整體來說流冰厚度與撞擊壓力和隧洞撞擊區位移還是均為多項式函數的關系。由圖13、圖14可以發現，當流冰厚度在16～20 cm變化的過程中，撞擊壓力峰值與X方向位移峰值均出現微小的下降趨勢，這是由于水介質和流冰厚度的尺寸效應共同導致的。本文所研究的是小塊流冰對隧洞襯砌的撞擊影響，在增加流冰厚度的過程中，流冰質量增加的相對較少，因此不同厚度流冰的撞擊壓力和撞擊區位移峰值差距會相應的較小，但是隨著流冰厚度的增加，水介質對于流冰的阻力相應的增大，對流冰速度的減緩作用增大，且流冰與隧洞襯砌的撞擊面積也相應的增大，因此撞擊壓力和隧洞襯砌X方向位移峰值會出現微小的下降趨勢，而不是線性增長的趨勢。

(1) 流冰厚度與撞擊壓力的關系式為

y=-58.739x2+17.865x+0.822 8

(4)

式中：y為撞擊壓力，MPa；x為流冰厚度，m； 相關系數為R2=0.988 5。

(2) 流冰厚度與隧洞襯砌撞擊區的位移關系式為

y=-0.002x2+0.000 6x-(1×10-5)

(5)

式中：y為隧洞襯砌碰撞區位移，m；x為流冰厚度，m； 相關系數為R2=0.913 3。

不同流冰厚度X方向位移峰值擬合曲線相關系數略低原因與4.1節分析原因一致。在此不再分析。

5 水介質中流冰撞擊隧洞襯砌的物理模型試驗

5.1 試驗方案設計

本文通過與數值模擬相對應的室內模型試驗對流冰與輸水隧洞襯砌的撞擊作用進行試驗驗證[20-21]。室內試驗模型與實際模型的幾何比尺Cl為 5，材料的密度比尺為1.0，加速度比尺為1.0[22-23]，在常重力場條件下進行試驗,試驗中水介質采用普通水介質。

試驗模型如圖9所示，圖中字母a，b，c，d，e點所代表的是應變片所在的位置，應變片布置高度為45 cm。

1.循環水管；2.固定支柱；3.水泵；4.水箱；5.旋轉螺旋；6.水槽；7.應變片(a, b, c, d, e)；8.測試儀器；9.測試線。圖15 試驗裝置圖Fig.15 Test device diagram

5.2 試驗內容

(1) 研究流冰壓縮強度對隧洞襯砌撞擊影響試驗。

在水箱中充滿水；打開總電源，利用水泵使得水箱中的水流入試驗隧洞模型中；將準備好的大小規格為 10 cm×10 cm×4 cm，屈服壓縮強度為1.825 MPa的冰塊放入隧洞模型中；通過旋轉螺旋將水流流速控制在3.0 m/s，流速用流速計測得；利用水位探針控制模型試驗水深為45 cm；檢查試驗模型邊壁的10 個有機玻璃應變片是否處于正確位置；關閉瞬態應變測試儀；利用測試線將10個有機玻璃應變片與瞬態應變測試儀進行相應的連接；將瞬態應變測試儀轉換為手動操作狀態；隨著流冰撞擊試驗模型邊壁，觀測并記錄瞬態應變測試儀上所顯示的數據；接著改變流冰壓縮強度大小，流冰壓縮強度由溫度來控制，選擇不同溫度來對應流冰壓縮強度，分別取流冰壓縮強度為2.136 MPa，2.357 MPa，2.528 MPa，2.668 MPa，2.786 MPa，2.889 MPa，2.979 MPa，3.059 MPa，3.133 MPa，3.199 MPa，重復上述步驟，最終進行數據整理。觀察流冰壓縮強度對撞擊壓力以及隧洞襯砌碰撞區位移的影響情況。

(2) 流冰厚度大小對撞擊影響的試驗。

改變工況，水深和流速均保持不變，改變流冰厚度，分別取1.2 cm，2.0 cm，2.6 cm，3.2 cm，3.6 cm，4.0 cm厚度流冰；重復上述步驟，觀察流冰厚度對撞擊壓力以及隧洞襯砌碰撞區位移的影響情況。

5.3 流冰壓縮強度對隧洞襯砌的撞擊影響

根據5.2節中試驗內容(1)所得的試驗數據，得到不同壓縮強度流冰工況下，隧洞襯砌所受的撞擊壓力值及隧洞襯砌撞擊區的位移值，將上述已處理過的試驗數據按照模型相似比進行相應的換算，得到如圖16所示的軟件模擬計算結果與試驗觀測計算結果對比圖。

圖16 不同壓縮強度流冰試驗結果與模擬結果對比圖Fig.16 Comparison of ice flow test results and simulation results with different compression strengths

由圖16可以發現，在流冰壓縮強度改變的條件下，數值模擬結果的最大峰值與試驗觀測結果所得最大峰值有基本一樣的趨勢，吻合效果良好。由圖16可以看出當流冰壓縮強度增大時，流冰對隧洞襯砌的撞擊壓力隨之增大，隧洞襯砌撞擊區的最大位移也隨之增大，且基本呈現出對數函數分布的關系。

通過誤差分析可以發現，在撞擊壓力方面：數值模擬所得的峰值結果與試驗觀測所得的峰值結果最大誤差為4.12%，最小誤差為 0.51%，平均相對誤差保持在 1.22%左右；在隧洞襯砌碰撞區最大位移方面：數值模擬所得的峰值結果與試驗觀測所得的峰值結果最大誤差為2.34%，最小誤差為 0.1%，平均相對誤差保持在 0.88%左右，其計算所得誤差均保持在允許范圍內[24]。由此可知，本文采用的仿真模型可以準確的模擬水介質中流冰與輸水隧洞襯砌的碰撞作用，模擬結果真實可靠。經過分析可知，誤差的產生主要是由于試驗值波動導致，可能與試驗中流冰與模型的二次碰撞以及水介質的作用有關。

5.4 流冰厚度對隧洞襯砌的撞擊影響

根據5.2節中試驗內容(2)所得的試驗數據，得到不同厚度流冰工況下，隧洞襯砌所受的撞擊壓力值及隧洞襯砌撞擊區的位移值，將上述已處理過的試驗數據按照模型相似比進行相應的換算，得到如圖17所示的軟件模擬計算結果與試驗觀測計算結果對比圖。

圖17 不同厚度流冰試驗結果與模擬結果對比圖Fig.17 Comparison of flow ice test results and simulation results with different thickness

由圖17可以發現，在流冰厚度改變的條件下，數值模擬結果的最大峰值與試驗觀測結果所得最大峰值有基本一樣的趨勢，吻合效果良好。由圖17可以看出當流冰厚度增大時，流冰對隧洞襯砌的撞擊壓力隨之增大，隧洞襯砌撞擊區的最大位移也隨之增大，且基本呈現出多項式函數分布的關系。

通過誤差分析可以發現，在撞擊壓力方面：數值模擬所得的峰值結果與試驗觀測所得的峰值結果最大誤差為1.91%，最小誤差為 0.1%，平均相對誤差保持在 1.17%左右；在隧洞襯砌碰撞區最大位移方面：數值模擬所得的峰值結果與試驗觀測所得的峰值結果最大誤差為4.85%，最小誤差為 0.17%，平均相對誤差保持在2.26%左右，其計算所得誤差均保持在允許范圍內。由此可知，本文采用的仿真模型可以準確的模擬水介質中流冰與輸水隧洞襯砌的碰撞作用，模擬結果真實可靠。經過分析可知，誤差的產生主要是由于試驗值波動導致，可能與試驗中流冰與模型的二次碰撞以及水介質的作用有關。

6 結 論

本文與先前研究所不同的是，考慮水介質對于流冰撞擊隧洞襯砌的影響，運用有限元分析軟件ANSYS/LS-DYNA進行了水介質中不同壓縮強度流冰以及不同厚度流冰對隧洞襯砌的碰撞仿真模擬，并開展了相應的室內模型試驗，經過研究發現數值模擬結果和試驗觀測結果具有良好的吻合性，并且根據流冰壓縮強度與流冰厚度的變化對輸水隧洞襯砌撞擊影響得到了以下結論：

(1) 在只改變流冰壓縮強度的情況下，隧洞撞擊區X方向位移峰值和撞擊壓力峰值均隨著流冰壓縮強度的增大而增大，且均呈現出對數函數關系，仿真模擬值與試驗觀測值誤差保持在5%以內。

(2) 在只改變流冰厚度的情況下，隧洞撞擊區X方向位移峰值和撞擊壓力峰值與流冰厚度呈現出近似多項式關系，仿真模擬值與試驗觀測值誤差保持在5%以內，且在本文所模擬的厚度工況下，當厚度在16～20 cm時，流冰撞擊壓力峰值及碰撞區X方向位移峰值不再隨著流冰厚度的增加呈現出增加的趨勢，而是由于水介質和流冰厚度尺寸效應的影響作用出現輕微的下降趨勢。

(3) 綜合分析本文所模擬的不同工況可以發現，水介質對于小型流冰撞擊隧洞襯砌過程有較大的影響，不可忽略，且“水墊效應”在碰撞過程中表現的較為明顯。

在實際工程中漂浮在水面的流冰其運動是受多因素影響的，如水溫與水流流態等；而對于水介質中中小型流冰長期碰撞隧洞襯砌導致其失效作用等問題，還需要做進一步的研究。因此，本文研究內容可以為后續流冰長期碰撞導致隧洞襯砌失效作用研究提供支持，也為西北寒旱地區流冰期輸水提供了理論基礎和技術保障。