多級齒輪傳動轉子系統的模態縮減與振動特性分析

韓健明， 楊 翼， 馬清雅， 王滋華， 戴義平

(西安交通大學 能源與動力工程學院，西安 710049)

齒輪傳動轉子系統在能源、電力、機械、化工、航空、船舶和車輛等行業的動力設備中起著重要作用，其動力學和振動特性直接影響到整機設備的振動噪聲和穩定運行，相關研究具有重要的理論價值和工程意義，受到國內外學者的廣泛重視。

對于單級齒輪傳動的兩軸系統，Rao等[1]提出了齒輪傳動轉子系統的通用有限元模型，對含減速齒輪的透平電機轉子系統進行了彎扭耦合自由振動分析，探究了齒輪嚙合剛度對固有頻率和模態振型的影響。Saxena等[2]利用ANSYS Workbench平臺對齒輪轉子系統進行了模態分析，并研究了軸承剛度的變化對系統固有頻率的影響。蔣慶磊等[3]建立了齒輪傳動轉子系統的通用模型，對大功率離心泵軸系進行了振動及響應分析，并研究了齒輪副耦合作用對振動特性的影響。結果在軸系設計和機組運行穩定性方面具有實際意義。車永強[4]采用有限元法計算了未耦合和耦合的齒輪-轉子系統的臨界轉速、振型、彎振不平衡響應和扭振不平衡響應。王逸龍等[5]以某航空發動機轉子為研究對象，基于集中參數法建立了帶阻尼環的齒輪傳動轉子系統的彎扭耦合動力學模型，分析了其在工作頻率范圍內的動力學響應。常樂浩等[6]提出了適用于平行軸外嚙合圓柱齒輪-軸-軸承-箱體系統動力學建模的有限單元法，并以一對單級斜齒輪傳動為例，通過與已有實驗數據的對比驗證了該方法的有效性。

對于多級多軸齒輪傳動轉子系統，龐輝等[7]分析了某三平行齒輪減速系統的固有頻率、振型和受迫振動響應特性，結果表明，多級齒輪傳動轉子系統的振動通常為各軸間的彎扭耦合振動，且各軸上的不平衡會引起整個系統的振動。張義民等[8]基于模態疊加法，對膨脹機系統進行了固有特性分析和瞬態方式的不平衡響應分析，得到齒輪嚙合前、后系統加載處的不平衡響應變化曲線。王奇斌[9]計算了齒輪傳動轉子系統在定轉速、變轉速下的不平衡響應以及靜態傳遞誤差引起的系統動力學響應。朱麗莎等[10]以壓縮機轉子系統為例，基于有限元法，建立了通用的彎-扭-軸-擺斜齒輪耦合動力學模型，并分析了系統的固有特性和不平衡響應。

綜上所述，國內外學者在單級或多級齒輪傳動轉子系統的建模和振動特性方面開展了大量的研究工作，文獻[11]研究了單級齒輪傳動轉子系統的模態縮減。然而，多級齒輪傳動轉子系統結構復雜、自由度多、求解時間長，而且由于齒輪耦合作用，多個轉子振動相互耦合，系統動力學行為復雜，有必要關注多級齒輪傳動轉子系統的簡化及其振動特性分析。因此，本文提出了一種適用于多級齒輪傳動轉子系統的模態縮減法，以某工程項目的透平驅動水泵系統為研究對象，通過有限元法建立了系統動力學模型，并利用模態縮減法減少了系統自由度。在此基礎上研究了系統的固有特性、不平衡量與靜態傳遞誤差引起的穩態響應、啟動狀態下的瞬態響應以及穩定運轉下突加不平衡時的瞬態響應。

1 齒輪傳動轉子系統有限元建模

1.1 齒輪嚙合模型

本文建立的12自由度斜齒輪三維動力學模型如圖1和圖2所示，齒輪副被簡化為兩個由彈簧-阻尼單元連接的剛性圓盤。r1與r2為齒輪基圓半徑；α12為齒輪的方位角，表示齒輪的相對位置；β12為螺旋角，主動輪左旋時大于0，右旋時小于0；ψ12為主動輪y軸正方向與嚙合平面的夾角。位移向量可表示為

圖1 斜齒輪副三維動力學模型Fig.1 Three-dimensional dynamic model of a helical gear pair

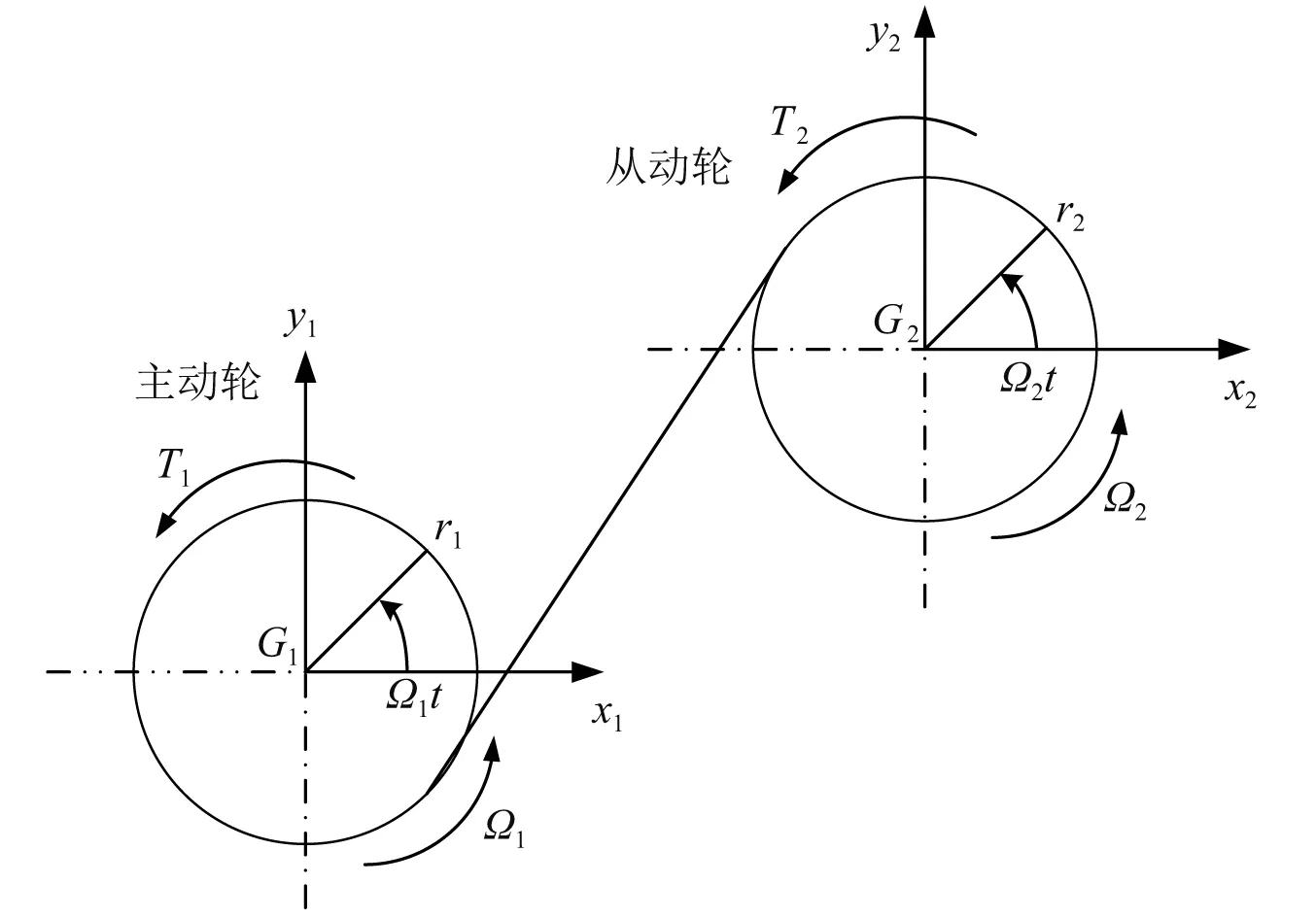
圖2 z方向投影圖Fig.2 Projection drawing in z-direction

qg=[x1,y1,z1,θx1,θy1,θz1,x2,y2,z2,θx2,θy2,θz2]T

(1)

式中：x，y和z為橫向自由度；θ為扭轉自由度。假設齒輪副受到不平衡激勵，根據牛頓第二定律，齒輪副的運動微分方程為

(2)

其中，

Mg,i=diag(mi,mi,mi,Iix,Iiy,Iiz)

(3)

(4)

qg,i=[xi,yi,zi,θxi,θyi,θzi]T

(5)

(6)

(7)

(8)

Tg,i=[0,0,0,0,0,Ti]T

(9)

(10)

(11)

式中：U為不平衡量；h12為齒輪副在嚙合線方向的相對位置，用位移向量表示為

h12(t)=[(-x1+x2)sinψ12+(y1-y2)cosψ12+
r1θz1+r2θz2]cosβ12+(z1-z2+r1θx1sinψ12+
r2θx2sinψ12-r1θy1cosψ12-
r2θy2cosψ12)sinβ12-e12(t)

(12)

式中，e12(t)為靜態傳遞誤差激勵，其定義為

e12(t)=e12sin(N1Ω1t)

(13)

式中：e12為幅值；N1，Ω1分別為主動輪1的齒數和轉速。

1.2 轉子系統模型

轉子系統的典型有限元模型由三部分組成：軸段、軸承和剛性圓盤。本文根據Stringer[12]所提出的方法建立軸段、軸承和剛性圓盤的有限元模型，獲得相應的質量矩陣M、陀螺矩陣G和剛度矩陣K。阻尼假設為比例阻尼。由此即可得到單個轉子系統的運動方程

(14)

式中：M，C和K為n階矩陣，分別表示質量、阻尼和剛度矩陣；F為外力矢量。阻尼矩陣包含兩部分，廣義阻尼矩陣D和反對稱的陀螺矩陣G。

2 模態縮減

2.1 坐標變換矩陣

Garvey等[13-14]提出了一種坐標變換的方法，可將單個轉子系統的運動方程式(14)轉換為一階狀態空間方程

(15)

其中，

(16)

式中，I為單位矩陣。這種坐標轉換方法的關鍵是得到兩個2n階的矩陣TL和TR， 使得它們滿足式(17)

(17)

式中，Md，Cd和Kd分別為對角化后的質量、阻尼及剛度矩陣。物理坐標與主坐標之間的轉換關系可表示為

u=TRv

(18)

(19)

通過以下4個步驟得到轉換矩陣TL和TR：

步驟1求解式(15)的特征值λi=αi±jβi并得到左右兩個特征向量矩陣ΦL和ΦR，ΦR為標準化后的特征向量矩陣。將特征值排列成兩個對角矩陣Λ1=diag[α1+jβ1,α2+jβ2,…,αn+jβn]和Λ2=diag[α1-jβ1,α2-jβ2,…,αn-jβn]。同時重新排列兩個特征向量矩陣ΦL和ΦR，使其中的特征向量與Λ1和Λ2中的特征值相對應。

步驟2計算得到矩陣Md，Cd和Kd。其中Md=I,Cd=diag[ci]，Kd=diag[ki]。ci和ki由式(20)得出

(20)

步驟3求解式(19)的特征值，并得到左特征向量矩陣EL和標準化后的右特征向量矩陣ER滿足式(21)

(21)

式中，Λ=diag[Λ1,Λ2]。

步驟4將式(21)進行變形

(22)

由此可得到

(23)

2.2 整體系統方程

假設齒輪轉子系統有m個軸，每個轉子視作一個子系統。將每個子系統的運動方程寫成式(15)的形式后，組裝得到整體系統的運動方程

(24)

式(24)簡寫為

(25)

式(25)所給出的整體系統的運動方程并沒有考慮齒輪嚙合效應。耦合了第i個和第j個轉子的齒輪嚙合剛度矩陣可寫為

(26)

Stringer等[15]認為單級齒輪傳動的兩軸系統的狀態空間矩陣表示為

(27)

對于一個n軸系統，式(27)應修改為

(28)

其中，

(29)

式中，Astif,k為耦合了第i個和第j個轉子的第k個齒輪嚙合剛度矩陣。對于一個m軸系統，至少應有m-1個齒輪副來保證系統的穩定運行。因此，k=1,2,…,N(N≥m-1)。這樣，整體的齒輪嚙合剛度矩陣就可表示為

(30)

根據整體齒輪嚙合剛度矩陣的形成方法同理可得整體齒輪嚙合阻尼矩陣Bdamp。由此，式(25)改寫為

(31)

整體的轉換矩陣TL,s和TR,s由各子系統的轉換矩陣TL,i和TR,i(i=1,2,…,n)組裝得到，組裝方法與式(24)類似。整體主坐標與物理坐標之間的關系表示為

us=TR,svs

(32)

(33)

3 結果與討論

3.1 有限元模型的驗證

為了不失一般性，通過現有文獻中一個實例來驗證上述有限元模型。以Rao等提出的透平電機轉子系統為驗證對象，該系統由透平轉子、電機轉子和直齒輪副組成。該轉子系統的簡圖如圖3所示。對于直齒輪來說，螺旋角為0°，其它參數與Rao等文中所給一致。齒輪嚙合剛度為1×108N/m時工作轉速下的固有頻率，如表1所示。同時，也給出了Rao等的計算結果作為對比。很明顯，兩組結果在各階固有頻率上都有著很好的一致性，證明了本文的有限元模型有著較高的精度。

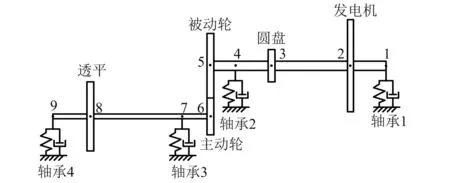
圖3 透平電機轉子系統模型Fig.3 Sketch diagram of the turbo-generator rotors system

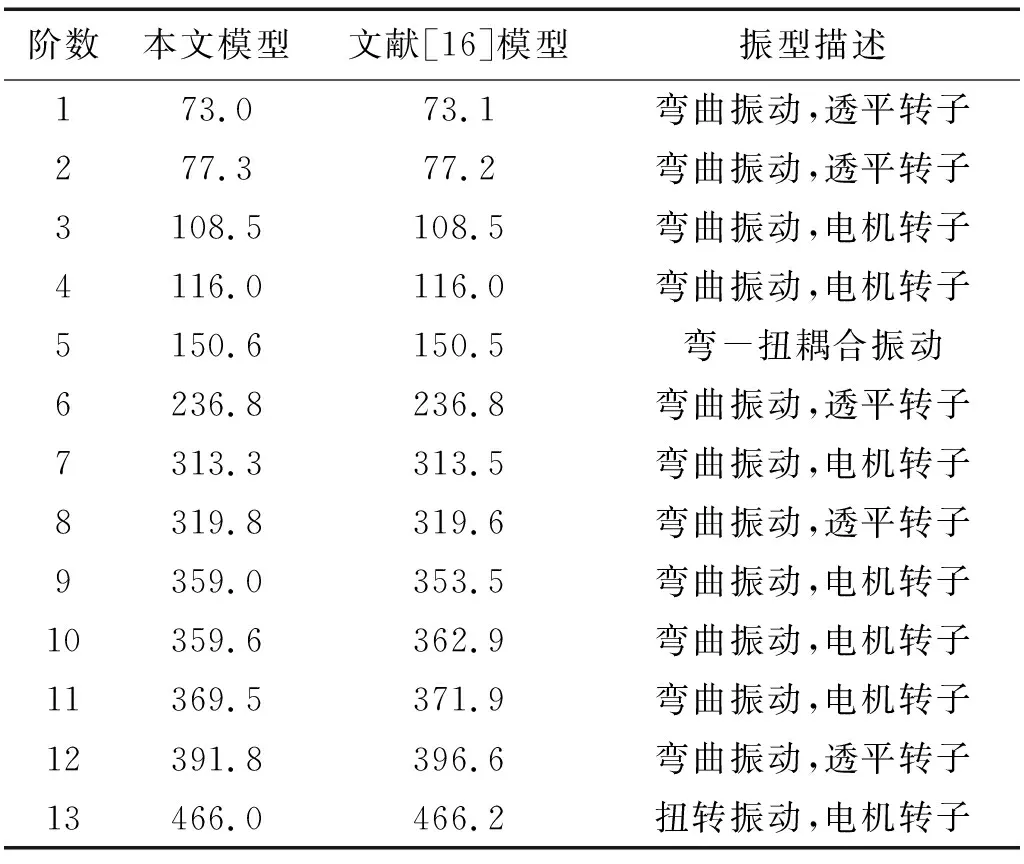
表1 透平電機轉子系統的固有頻率Tab.1 Natural frequencies of the turbo-generator rotors system (rad/s)

3.2 固有頻率分析

以某工程項目的透平驅動水泵系統為研究對象，系統結構如圖4所示。透平轉子的工作轉速為5 600 r/min。一級齒輪傳動比為33/122，齒輪嚙合剛度為2.85×108N/m，模數為4 mm，壓力角為20°。二級齒輪傳動比為34/87，齒輪嚙合剛度為3.42×108N/m，模數為8 mm，壓力角為20°。軸承B7，B8，B9和B10是滾動軸承，其它為滑動軸承。圖5為該系統所對應的等效系統圖。整個系統劃分為36個節點，共216個自由度。

圖4 透平驅動水泵系統Fig.4 Sketch diagram of the turbine driven pump system

圖5 等效系統圖Fig.5 The diagram of equivalent system

圖6和圖7分別為未耦合與耦合系統的Campell圖。從中可以看出，齒輪耦合改變了系統的模態。相比于未耦合系統，耦合系統出現了兩個新的固有頻率，如圖7中箭頭所示。未耦合系統的1階、2階、3階和4階模態與耦合系統的3階、4階、5階和6階模態相差不大。相比于未耦合系統，耦合系統的部分固有頻率如7階、8階減小了。這是由于齒輪將各轉子耦合在一起后相當于增加了轉子長度，因此部分受耦合效應影響的固有頻率有所降低。此外，受陀螺效應影響，固有頻率隨轉速的變化而變化，但變化并不明顯。

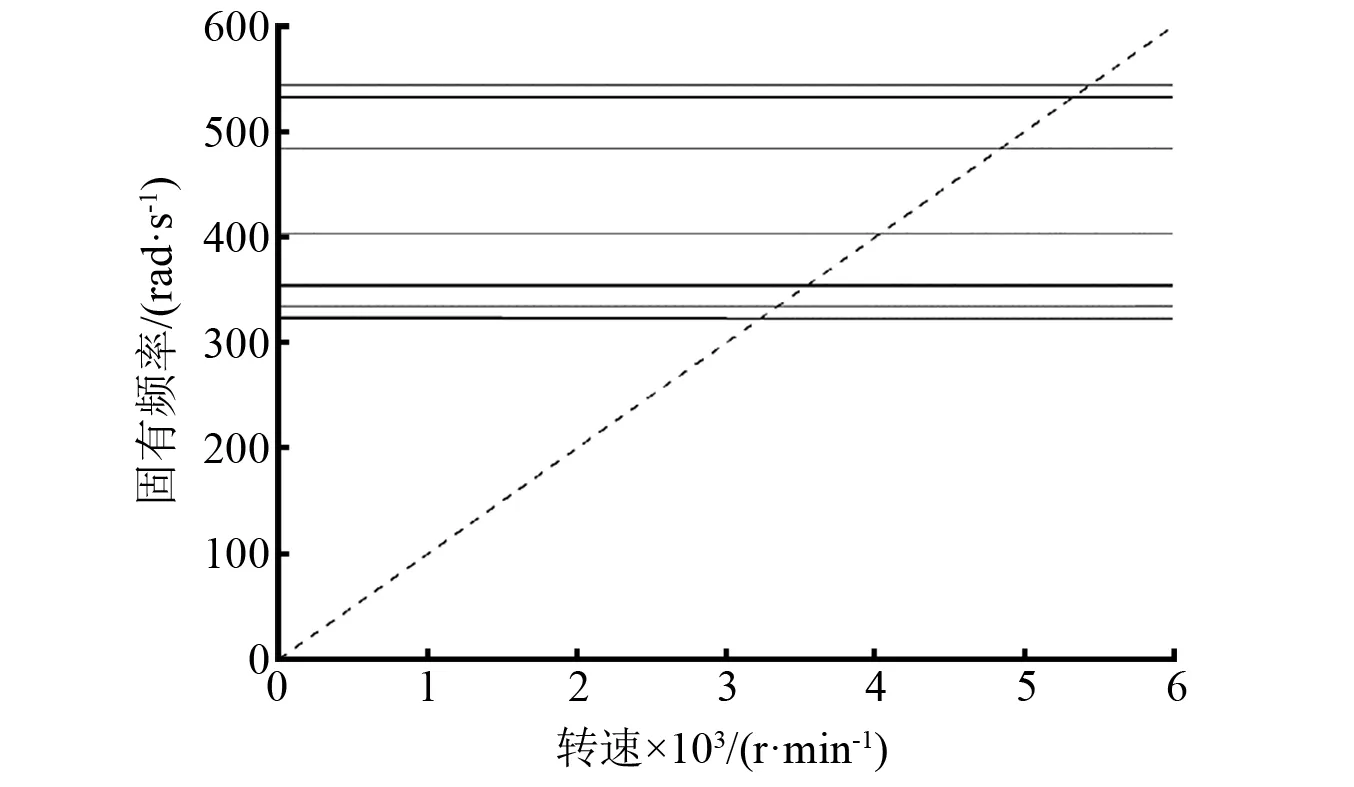
圖6 未耦合系統的Campell圖Fig.6 The Campell diagram of uncoupled system

圖7 耦合系統的Campell圖Fig.7 The Campell diagram of coupled system

表2為完整自由度模型(216個自由度)與100個、80個、60個、40個自由度模型在工作轉速下的前14階固有頻率，同時也給出了相應的偏差(以完整模型結果為標準)。當保留60個自由度時最大偏差僅為1.32%，保留40個自由度時最大偏差也僅為2.25%，意味著僅需要較少的自由度即可很好地預測系統的固有頻率。

表2 工作轉速下固有頻率的偏差Tab.2 Error percents of natural frequencies at operational speed

3.3 穩態響應分析

本節對不平衡量及靜態傳遞誤差引起的穩態響應進行分析。根據美國石油協會標準[17]確定系統不平衡量的施加位置和大小，在D5處施加不平衡量2 004 g·mm。圖8是系統D7處的不平衡響應曲線。可以看出，在給定轉速范圍0～7 000 r/min內，僅在臨界轉速3 087 r/min附近有一個波峰。相比于完整模型，縮減后的模型仍然具有很高的精度。

圖8 系統D7處不平衡響應Fig.8 Response due to mass unbalance of D7

齒輪嚙合的靜態傳遞誤差是指實際嚙合位置與理論位置在嚙合線上的偏差。齒輪的加工安裝誤差和變形都會引起傳遞誤差。靜態傳遞誤差幅值為0.5×10-6m，頻率為齒輪嚙合頻率。系統D7處的響應曲線如圖9所示。在給定的轉速范圍0～7 000 r/min內存在多個峰值，且0～1 000 r/min內存在最大峰值。這說明靜態傳遞誤差激勵在低轉速范圍內(0～1 000 r/min)就可以激發系統的高階模態，引起系統劇烈振動，因此在對齒輪動力學的設計和分析中有必要重視靜態傳遞誤差激勵的作用和影響。在轉速大于2 000 r/min之后，40個自由度模型計算出的結果偏差較大，這是因為靜態傳遞誤差激勵可以在低轉速下激發系統的高階模態，當縮減了較多的自由度后，一些高階模態被丟棄，導致精度下降。所以在計算靜態傳遞誤差引起的響應時，應保留一定數量的自由度。

圖9 系統D7處靜態傳遞誤差激勵引起的響應Fig.9 Response due to static transmission error of D7

3.4 瞬態響應分析

首先對系統啟動時的瞬態響應進行分析。在圓盤D7處給定一初始不平衡量U=156 g·mm。為簡化計算，將透平的啟動規律進行簡化，使其以111.28 rad/s2的加速度啟動至工作轉速。采用4～5階自適應變步長的龍格庫塔法求解系統的運動方程，并獲得了啟動響應曲線。系統啟動過程中X和Y方向的振幅如圖10和圖11所示。從圖中可以看出，在系統啟動至1.5 s，4 s以及5 s附近時，振幅增大，振動劇烈，相應的轉速分別接近于轉速為1 883 r/min，4 120 r/min和5 036 r/min的臨界轉速。完整自由度模型與100個、80個、60個、40個自由度模型的計算時間分別為69 856.77 s，3 016.49 s，1 601.74 s，542.46 s和119.37 s。

圖10 啟動狀態下D7處X方向振幅Fig.10 X-direction amplitude at D7 in the startup state

圖11 啟動狀態下D7處Y方向振幅Fig.11 Y-direction amplitude at D7 in the startup state

轉子系統在運轉過程中可能由于轉子零件松脫或葉片斷裂等原因造成不平衡量突然增大，為研究這種情況下的瞬態響應特性，當系統運轉至某一時刻時，將系統不平衡量增大至780 g·mm。突加不平衡后轉子系統在工作轉速下的瞬態響應特性如圖12和圖13所示。從圖中可以看出，在轉子系統運轉至1 s時突加不平衡，經過一段時間后瞬態響應消失，進入穩態階段。計算具有216個、100個、80個、60個、40個自由度的模型所需要的時間分別為20 753.05 s，789.80 s，412.42 s，132.36 s和33.17 s。

圖12 工作轉速下突加不平衡D7處X方向振幅Fig.12 X-direction amplitude at D7 due to unbalance mutation at the operating speed

圖13 工作轉速下突加不平衡D7處Y方向振幅Fig.13 Y-direction amplitude at D7 due to unbalance mutation at the operating speed

相比于完整自由度模型，縮減自由度模型節省計算時間超過90%。表3為局部放大圖中某一時刻不同自由度模型的振幅之間的偏差。以完整自由度模型為基準，縮減自由度模型結果的最大偏差僅為0.36%，說明僅需要很少的自由度參與計算，即可很好地預測系統的瞬態響應特性。

表3 瞬態響應振幅之間的偏差Tab.3 Error percents between transient response amplitude

4 結 論

本文采用有限元法，建立了多級多軸齒輪傳動轉子系統動力學模型，利用模態縮減法減少了系統自由度，并對縮減模型的準確性進行了驗證，在此基礎上研究了系統的振動響應特性，得到了如下結論：

(1) 齒輪耦合作用使系統產生了新的固有頻率。此外，由于齒輪將各轉子耦合在一起后相當于增加了轉子長度，部分固有頻率有所降低。

(2) 對于不平衡響應，相比于完整模型，縮減后的模型仍然具有很高的精度。靜態傳遞誤差激勵在低速范圍內(0～1 000 r/min)即可激發系統的高階模態。因此，為保證計算精度，在計算靜態傳遞誤差激勵引起的響應時應保留一定數量的自由度。

(3) 在啟動過程中，由于自身不平衡量的作用，系統穿越臨界轉速時會發生不同程度的振動。在系統啟動至1.5 s，4 s以及5 s附近的轉速分別對應于轉速為1 883 r/min，4 120 r/min和5 036 r/min的臨界轉速。當不平衡量發生突變時，系統發生劇烈振動，經過一段時間后瞬態階段消失，進入穩態階段。

(4) 利用模態縮減法剔除高階模態后，大大縮減了計算時間。相比于完整自由度模型，縮減后的模型精度高，偏差小。因此，本文提出的模態縮減法在節省計算時間的同時也保證了計算準確性。