既有橋梁對相鄰車-橋系統氣動力的影響分析

嚴乃杰， 吳 韜， 臧 瑜， 李永樂， 鄭博文， 戴建國

(1. 中國鐵道科學研究院集團有限公司 鐵道建筑研究所，北京 100081； 2. 西南交通大學 土木工程學院，成都 610031；3. 重慶市軌道交通(集團)有限公司，重慶 401120； 4. 上海市政設計工程研究總院(集團)有限公司，上海 200092)

隨著城市交通的快速發展，城市橋位資源越來越寶貴，為了滿足交通需求，常常需要在既有橋梁附近新建橋梁，如2007年通車的塔科馬大橋平行橋，距原塔科馬大橋僅61 m；2011年通車的新海河大橋，距原海河大橋僅35 m。當既有橋梁位于新建橋梁來流前方時，既有橋梁會干擾新建橋梁周圍的流場，對作用在新建橋梁及橋上列車的氣動荷載產生影響。已有研究表明：列車在橋梁、高路堤等結構物上運行時，在橫向風荷載作用下，列車更容易發生列車傾覆等事故[1]。因此，橋上列車的氣動特性也成為近年來的研究熱點。對于大跨度軌道交通橋梁，主梁離地較高，橋面風荷載較大，導致橋上列車對風荷載的作用更敏感，車-橋系統受橫向風的影響更明顯，且作用在列車、橋梁上的氣動力與車輛的位置密切相關，既有橋梁對新建橋梁車-橋系統氣動力的干擾也更為復雜。

目前，國內外學者針對相鄰橋梁的氣動干擾現象開展了諸多研究。針對新建的塔科馬平行橋，Irwin等[2]進行了節段模型和全橋氣彈模型風洞試驗，研究了兩座橋梁間的氣動干擾效應，包括施工狀態、成橋狀態的風荷載和氣動穩定性。陳政清等[3-4]以平勝大橋、紅島航道斜拉橋為背景，研究了平行雙箱梁橋面的顫振、渦振、靜力氣動特性，并分析了箱梁距離與氣動干擾間的關系，結果表明相鄰橋梁之間存在不可忽略的氣動干擾。朱樂東等[5-6]以新建的海河大橋為背景，研究了既有橋梁對鄰近新建橋梁顫振、渦振性能和氣動力系數的影響。劉小兵等[7]引入干擾因子概念，研究了三種典型橋梁斷面相互間的氣動干擾效應，結果表明鈍體斷面的干擾效應更明顯。秦浩等[8-9]通過全橋氣彈模型試驗、數值模擬，研究了大跨度雙幅鋼箱梁橋渦振特性，以及中央格柵抑制渦振的效果。JTG/T 3360-01—2018《公路橋梁抗風設計規范》指出：分離雙幅橋梁凈間距小于5倍單幅主梁寬度時，單幅橋梁的橫向力系數的確定宜考慮雙幅橋梁的氣動力干擾效應。上述研究結果表明，相鄰橋梁之間的氣動干擾效應顯著，在橋梁的設計中有必要考慮既有橋梁的影響。

已有研究均是針對相鄰橋梁加勁梁間的氣動干擾，如加勁梁顫振、渦振性能和靜風特性等，關于既有橋梁對相鄰車-橋系統的氣動力干擾研究還未見報道。本文以某新建的懸索橋為工程背景，通過節段模型風洞試驗，測試了考慮、不考慮既有橋梁干擾兩種工況下車-橋系統的氣動力系數，研究了既有橋梁對鄰近車-橋系統氣動力系數的影響。結合試驗結果，模擬了車-橋系統抖振力時程，通過極值概率分布計算了車-橋系統抖振力的極值，分析了既有橋梁對鄰近車-橋系統抖振力的干擾效應。

1 工程概況

本文以某新建的雙塔三跨連續鋼箱梁懸索橋為工程背景，該橋為城市軌道交通橋梁，設計時速80 km/h，跨徑布置為50 m+210 m +600 m +210 m +50 m，梁寬22.0 m、高4.5 m，橋面布置人行道護欄、防拋網、疏散平臺等附屬設施，鋼箱梁橫斷面如圖1所示。在新建橋梁下游有一座既有橋梁，為雙塔三跨連續鋼箱梁公路懸索橋，跨徑布置為211 m +600 m +211 m，梁寬35.5 m、高3.0 m，橋面布置了人行道護欄、中央分隔帶，鋼箱梁橫斷面如圖2所示。兩座橋梁軸線水平距離70 m，豎向高度差3.45 m。新建橋梁橋面設施數量多，橋面風環境相對復雜，且為軌道交通橋梁，車-橋系統對風荷載更加敏感。因此，本文主要研究既有橋梁對相鄰新建橋梁車-橋系統氣動力的影響。

圖1 新建橋梁鋼箱梁橫斷面(m)Fig.1 Cross-section of steel box girder of new-built bridge (m)

圖2 既有橋梁鋼箱梁橫斷面(m)Fig.2 Cross-section of steel box girder of existing bridge (m)

2 車-橋系統氣動力模型

2.1 靜風力

作用在單位長度橋梁上的靜風力可以表示為

(1)

(2)

(3)

列車的截面形式為矩形，繞軸心的扭轉力矩對列車響應的貢獻較小，可以忽略不計[10]。當風速垂直于列車運動方向時，作用在單位長度列車上的靜風力可表示為

(4)

(5)

2.2 抖振力

體軸坐標系下，作用在單位長度橋梁上的抖振力可以表示為

(6)

(7)

(8)

式中：FH為橋梁抖振阻力；FV為橋梁抖振升力；MT為橋梁抖振升力矩；χ為導納函數；u(t)為順風向脈動風；w(t)為豎向脈動風。

研究中通常僅考慮順風向脈動風對列車抖振力的貢獻[11]。然而，已有研究表明橫向風和豎向脈動風對列車抖振力的影響不容忽視[12]。為了更真實地模擬作用在移動列車上的抖振力，本研究同時考慮了順風向、橫風向和豎向脈動風。體軸坐標系下，作用在單位長度列車的抖振力可以表示為

(9)

(10)

式中：FS為列車抖振橫向力；FL為列車抖振升力；v(t)為橫風向脈動風；χiu，χiv，χiw為與不同風向脈動風有關的導納函數；Ciu，Civ，Ciw為與抖振力有關的氣動力系數，i=S,L。根據Yan等的推導結果，上述抖振力系數可表示為

(11)

(12)

(13)

3 車-橋系統氣動特性風洞試驗

試驗在西南交通大學XNJD-1風洞第二試驗段進行，試驗段寬2.4 m、高2.0 m，風速范圍為1.0～45.0 m/s。列車和橋梁模型縮尺比取1/40，模型長2.095 m，其中列車模型寬75 mm，高87.5 mm，風洞中車-橋系統節段模型如圖3(a)所示。通過交叉滑槽系統實現橋梁、列車氣動力分離，測試了考慮、不考慮既有橋梁影響兩種狀態下新建橋梁車-橋系統氣動力系數。考慮既有橋梁影響下的車-橋系統節段模型，如圖3(b)所示。

低風速下雷諾數較小，高風速下車-橋模型會發生振動而影響試驗結果。因此，試驗風速取15 m/s。試驗中使用了一種自主研發的車-橋系統三分力測試裝置——交叉滑槽系統，該裝置能夠實現車-橋系統的同軸轉動，并能分別測試出車-橋系統中列車、橋梁的三分力，從而方便地進行不同攻角情況下的氣動力的試驗[13]。試驗中分別測試了-3°～+3°風攻角下，考慮、不考慮既有橋梁影響時新建橋梁上無車/單車/雙車組合工況下車-橋系統的氣動力系數，試驗工況如表1所示，試驗結果如表2和表3所示。其中，單橋不考慮既有橋梁的影響；雙橋考慮了既有橋梁的影響，且既有橋梁位于新建橋梁的來流前方，如圖3(b)所示。

圖3 車-橋系統節段模型Fig.3 Segmental model of vehicle-bridge system

表1 風洞試驗工況Tab.1 Cases of wind tunnel test

由表2可知，受既有橋梁影響，當風攻角為-3°，0°時，不同位置列車的橫向力系數均增大，升力系數基本均減小；其中，0°風攻角下單車過橋時背風側列車橫向力系數增幅最大，為39.3%；-3°風攻角下雙車過橋時背風側列車升力系數減幅最大，為-68.2%。當風攻角為+3°時，不同位置列車的橫向力系數基本均減小，升力系數基本均增大；其中，雙車過橋時背風側列車橫向力系數減幅最大，為-143.1%；單車過橋時背風側列車升力系數增幅最大，為52%。需要注意的是：雙車過橋時，受迎風側列車的遮擋，背風側列車的氣動力系數均顯著小于迎風側的。

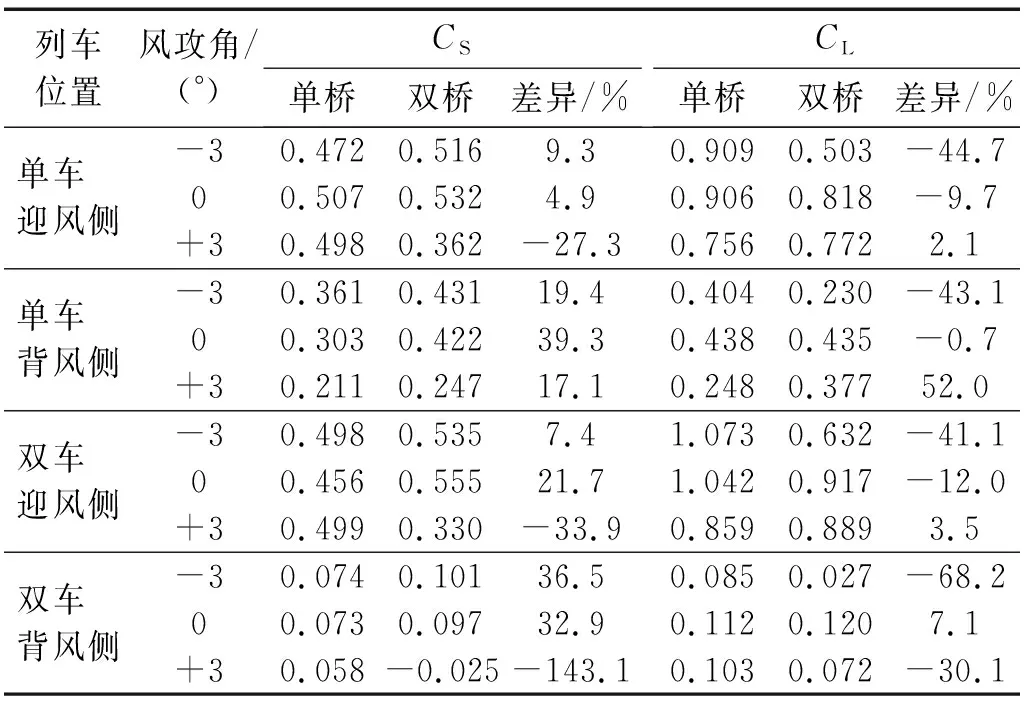
表2 列車氣動力系數Tab.2 Three-component coefficients of vehicle

由表3可知，受既有橋梁影響，不同工況下橋梁的阻力系數均減小，且減幅隨著風攻角的增大而增大，升力矩系數基本均增大；其中，+3°風攻角橋面無車情況下阻力系數減幅最大，為-22.4%；0°風攻角橋面無車情況下升力矩系數增幅最大，為200.6%。當風攻角為-3°時，不同工況下橋梁的升力系數均增大，最大增幅為29.2%；其余風攻角下橋梁升力系數的變化規律不明顯。

表3 橋梁氣動力系數Tab.3 Three-component coefficients of bridge

綜上所述，受既有橋梁影響，相鄰車-橋系統的氣動力系數變化明顯，表明既有橋梁對鄰近車-橋系統的氣動干擾效應顯著，且部分工況下列車、橋梁的氣動力系數大幅增大，對結構的整體抗風性能不利。因此，結構設計中應充分考慮既有橋梁對鄰近新建車-橋系統靜風荷載的影響。受既有橋梁干擾，相鄰車-橋系統中列車的氣動力系數變化幅度相對較大，表明橋上列車的靜風荷載受既有橋梁的影響更大。

4 車-橋系統抖振力影響分析

4.1 風場模擬

由列車、橋梁的抖振力表達式可知，橋梁抖振力與順風向和豎向脈動風有關，列車抖振力與順風向、橫風向和豎向脈動風有關。為了研究既有橋梁對鄰近車-橋系統抖振力的影響，首先需要模擬相對于靜止橋梁和移動列車的脈動風場。

模擬相對于橋梁的脈動風場較為容易，但是列車是移動的，模擬相對于移動列車的脈動風場則較為復雜。常用方法是沿順橋向模擬大量離散的脈動風場，然后插值選取不同位置風場不同時刻的脈動風速值構造出相對于移動列車的脈動風場。當模擬點數量線性增加時，計算量則呈指數型增長，使用該方法模擬移動列車時程計算量大、效率低。此外，插值選取風速值將導致構造的移動列車脈動風時程不連續而產生“突變”。另一種方法是使用相對于移動列車的脈動風譜，直接模擬相對于移動列車的脈動風時程，避免模擬大量離散風場，可有效減少計算量[14-15]。

本文采用Yan等推導的相對于移動列車的脈動風譜

(14)

(15)

Sξξ(Δy,f)=Cohξ(Δy,f)Sξ(f)

(16)

式中：Sξ′ξ′(Δη,f)為相對于移動列車風場的互譜，ξ=u,v,w；Rξ′ξ′(Δη,τ)為相對于移動列車風場的互相關函數；Sξξ(Δy,f)為相對于脈動風互譜；Sξ(f)為常用脈動風自譜；Cohξ(Δy,f)為風場相干函數；τ′=Δx/U為時間間隔，其中Δx=(Vtrτ-Δη)cosφ0， Δy=(Vtrτ-Δη)sinφ0； Δη為列車上風場模擬點間距；φ0為平均風速與車速的夾角，當風速垂直于列車運行方向時φ0=90°。當Δη=0時，式(14)便為相對于移動列車的脈動風場自譜。

將順風向和橫風向Simiu譜、Lumley-Panofsky豎向風譜和Davenport相干函數代入上述公式，便可得到對應風環境下相對于移動列車的風譜。取風速U=25 m/s、車速Vtr=80 km/h，時間步長Δt=0.25 s，風向角φ0=90°，通過諧波合成法分別模擬相對于橋梁和移動列車的脈動風時程，如圖4、圖5所示。

圖4 相對于橋梁的脈動風時程Fig.4 Time histories of turbulence relative to bridge

圖5 相對于移動列車的脈動風時程Fig.5 Time histories of turbulence relative to moving vehicle

4.2 移動列車抖振力時程

為了簡化研究，列車、橋梁的導納函數取1.0。基于上述模擬的脈動風場，分別模擬考慮、不考慮既有橋梁影響工況下單車、雙車過橋時作用在列車、橋梁上的抖振力。橋上無車、單車、雙車情況下，車-橋系統抖振力時程的影響如圖6～圖9所示。

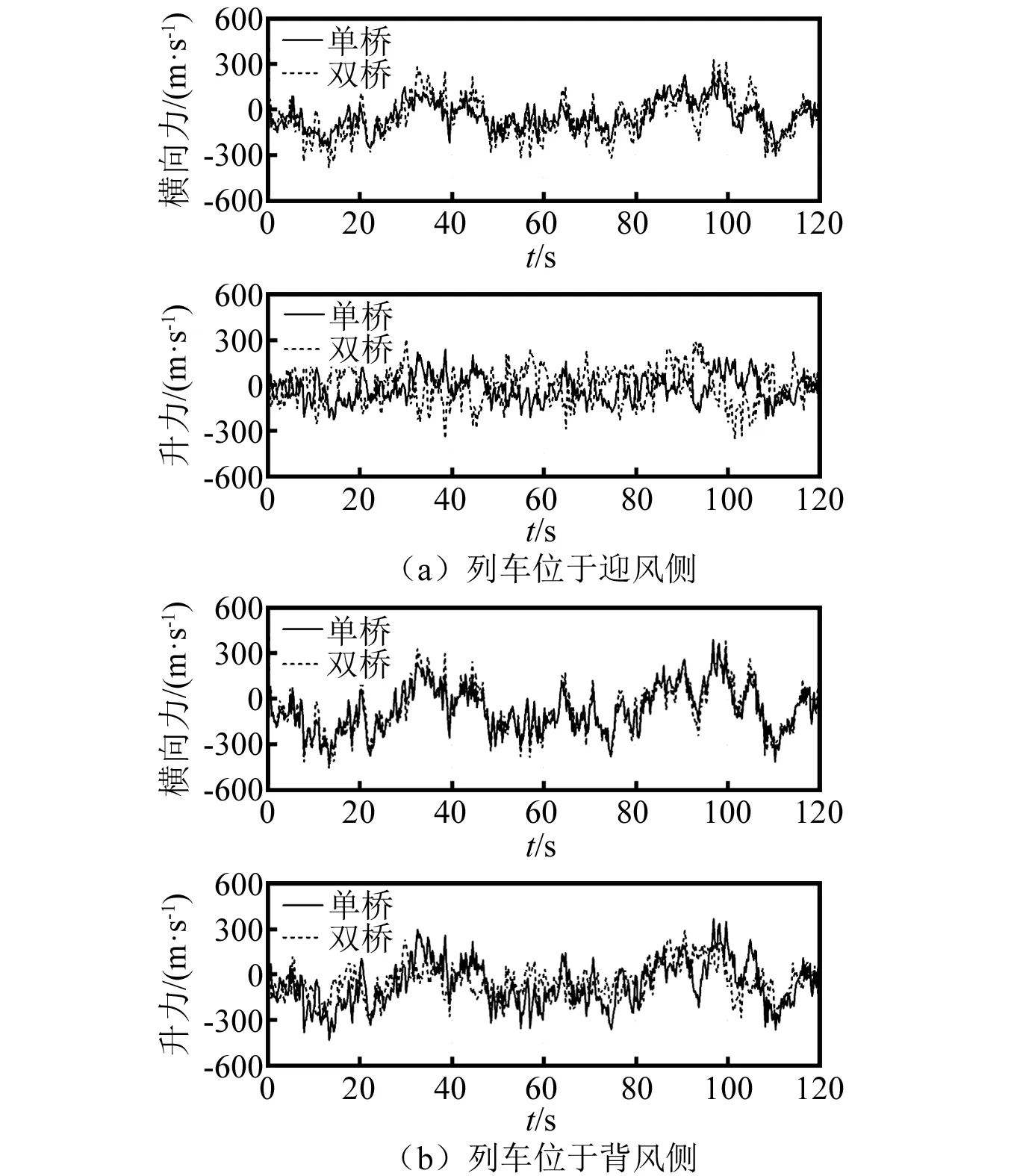
圖6 單車過橋時移動列車的抖振力Fig.6 Buffeting forces of moving vehicle as one vehicle moving on bridge

由圖6、圖7可知，受既有橋梁影響，單車/雙車過橋時，迎風側列車抖振橫向力、抖振升力幅值均顯著增大；背風側列車的抖振橫向力幅值略有增大。其中，單車情況下，背風側列車抖振升力幅值略有減小；雙車情況下，背風側列車抖振升力幅值基本不變。

圖7 雙車過橋時移動列車的抖振力Fig.7 Buffeting forces of moving vehicle as two vehicles moving on bridge

由圖8、圖9可知，受既有橋梁影響，各工況下相鄰橋梁的抖振阻力幅值均減小，抖振升力和升力矩的幅值略有增大。由圖8、圖9可知，當橋上有車時，作用在橋梁上的抖振力升力、升力矩幅值顯著大于橋上無車工況下的，表明列車對橋梁產生影響，導致作用在橋梁上的抖振升力、抖振升力矩增大。

圖8 單車過橋時橋梁的抖振力Fig.8 Buffeting forces of bridge as one vehicle moving on bridge

圖9 橋上無車、雙車過橋時橋梁的抖振力Fig.9 Buffeting forces of bridge as no vehicles or two vehicles moving on bridge

綜上所述，既有橋梁對相鄰橋梁上迎風側列車抖振力的影響顯著，且抖振力幅值受既有橋梁的影響而顯著增大；背風側列車抖振力受到的影響相對較小，其中，抖振橫向力幅值略有增大，抖振升力基本不變。較之橋上列車，鄰近橋梁受既有橋梁影響相對較小，其中抖振阻力幅值均減小，抖振升力和升力矩幅值略有增大。

4.3 抖振力極值

橫向風作用下，車-橋系統響應極值主要受風速極值控制，即脈動風極值。研究中通常將脈動風視為各臺歷經零均值的平穩高斯過程，則抖振力也為各臺歷經零均值的平穩高斯過程。零均值平穩隨機過程的極值服從穿越率基于泊松假定的極值概率分布，則時長T內不同超越概率下抖振力極值可以表示為

(17)

(18)

(19)

式中：Fmax為超越概率pf下抖振力的極值，即抖振力大于Fmax的概率為pf；v0為穿越率；λn為抖振力譜SF(f)的第n階矩。

為了進一步研究既有橋梁對鄰近橋梁車-橋系統抖振力極值的影響，取時長T=10 min，分別計算5%超越概率下上述工況列車、橋梁抖振力的極值，計算結果如表4、表5所示。

由表4可知，受既有橋梁影響，相鄰橋梁上迎風側列車抖振力極值顯著增大；背風側列車抖振橫向力極值略有增大，抖振升力極值略有減小。其中，雙車情況下迎風側列車抖振橫向力增幅最大，為35.2%；單車情況下迎風側列車抖振升力增幅最大，為67%。

表4 列車抖振力極值Tab.4 Exreme values of buffeting forces of vehicle

由表5可知，受既有橋梁影響，不同工況下相鄰橋梁抖振阻力極值均減小，抖振升力和抖振升力矩極值均增大，且抖振升力極值增幅最大。通過對比可知，橋上有車時，相鄰橋梁抖振阻力極值受既有橋梁干擾而減小的幅度比橋上無車工況下的小，表明橋上有車時，既有橋梁對相鄰橋梁抖振阻力的干擾效應大于無車情況下的。雙車情況下，相鄰橋梁的抖振力極值變化幅度最大，抖振阻力減小22.9%、抖振升力增大48.5%、抖振升力矩增大37.5%，表明雙車過橋時橋梁抖振力極值受既有橋梁的影響最大。

表5 橋梁抖振力極值Tab.5 Extreme values of buffeting forces of bridge

綜上所述，車-橋系統抖振力極值受既有橋梁的干擾顯著。受既有橋梁的影響，除了背風側列車抖振升力和橋梁抖振阻力的極值減小，車-橋系統其余抖振力極值均顯著增大。因此，結構設計中應充分考慮既有橋梁對相鄰車-橋系統抖振力的影響。

5 結 論

通過節段模型風洞試驗、數值模擬，本文研究了既有橋梁對相鄰車-橋系統氣動力的影響，得到以下結論：

(1) 既有橋梁對相鄰車-橋系統氣動力影響顯著，會導致部分工況下列車、橋梁的氣動力系數、抖振力顯著增大，對結構的整體抗風性能不利，結構設計過程中應該充分考慮既有橋梁對鄰近新建車-橋系統氣動力的干擾效應。

(2) 既有橋梁對相鄰車-橋系統氣動力的影響與列車的位置、風攻角有關，并呈現一定的變化規律。其中，列車的氣動力系數、抖振力受既有橋梁的影響更為顯著。

(3) 受既有橋梁影響，迎風側列車抖振力幅值均顯著增大，背風側列車的抖振力幅值變化較小。相鄰橋梁的抖振阻力幅值減小，抖振升力和升力矩的幅值增大。

(4) 車-橋系統抖振力極值受既有橋梁的干擾顯著。受既有橋梁的影響，除了背風側列車抖振升力和橋梁抖振阻力的極值減小，車-橋系統其余抖振力極值均顯著增大。