大型浮筏姿態及彈性變形控制算法研究

秦文政， 施 亮

(1. 海軍工程大學 振動與噪聲研究所，武漢 430033； 2. 船舶振動噪聲重點實驗室，武漢 430033)

將氣囊隔振器應用于浮筏隔振系統，可以顯著提高浮筏隔振效果，但也會帶來筏架姿態平衡欠佳的問題[1]。目前，國內學者已經在浮筏姿態平衡控制[2-5]、軸系對中控制[6-9]等方面開展了大量研究工作，并取得了較好的控制效果。

然而，隨著浮筏氣囊隔振系統趨于大型化[10-11]，其筏體結構剛度不可避免的降低。在外界擾動作用下，筏架不僅會偏離平衡位置，還會產生較大的彈性變形，造成筏上設備之間、設備與外接管路之間產生較大的相對位移，嚴重時容易超出其許用位移，危及設備運行安全。此外，筏架的彈性變形還可能影響主機與軸系的對中安全性，如圖1所示。因此，對大型浮筏氣囊隔振系統而言，不僅需要控制筏架姿態平衡，還必須考慮筏架彈性變形的控制問題。

圖1 某大型浮筏氣囊隔振系統示意圖Fig.1 Diagram of a large floating raft air spring isolation device

上述文獻中的氣囊控制方法對結構剛度較大的中小型筏架姿態平衡問題具有理想的控制效果，但尚未涉及大型筏架彈性變形的控制問題。

本文對大型浮筏氣囊隔振系統筏架姿態和彈性變形控制問題進行了研究。建立了某船舶浮筏隔振裝置柔性筏架響應模型，并在此基礎上提出了一種基于氣囊壓力參數識別的控制方法，最后在試驗平臺上進行試驗。試驗結果表明：該方法不僅可以控制筏架姿態平衡，還能夠有效抑制筏架彈性變形，并且具有較高的控制精度。

1 柔性筏架響應模型

以某船舶大型浮筏隔振裝置為研究對象如圖2所示，建立了該裝置的柔性筏架響應模型。其中，筏體尺寸為10.0 m×6.5 m×2.0 m；在筏架兩舷側均勻布置20個氣囊隔振器；另布置6個位移傳感器用于監測筏架姿態和彈性變形。

圖2 浮筏氣囊隔振系統示意圖Fig.2 The sketch of floating raft air spring isolation device

建立以系統重心為原點的總體坐標系O-XYZ和以各氣囊重心為原點的局部坐標系oi-xiyizi。根據文獻[12-13]，可得到浮筏剛體靜力學模型，其靜力學方程表達式為

Kxc=F

(1)

式中：K為系統總體剛度矩陣；xc為系統重心在O-XYZ坐標系中的平動位移和繞各坐標軸的轉動角度；F為系統受到的外力。

氣囊在額定高度附近工作時，其有效面積Se可近似為常數[14]，此時氣囊承載變化ΔF與壓力變化ΔP的關系可表示為

ΔF=ΔP·Se

(2)

由式(1)和式(2)經坐標變換可得到任一氣囊充/放氣時剛體筏架響應位移dij。

在浮筏剛體靜力學模型的基礎上，針對筏架彈性變形的特點，引入筏架響應修正系數矩陣，表達式為

(3)

式中：Ac，Af分別為充氣、放氣條件下筏架響應修正系數矩陣；aij為第i個氣囊在j號傳感器處筏架的響應修正系數，表達式為

(4)

由式(1)～式(4)可求得任一氣囊調整后柔性筏架響應理論值

(5)

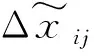
綜上，依據此柔性筏架響應模型，可預判任一氣囊充/放氣操作后筏架的調整效果。

2 控制性能指標

2.1 筏架彈性變形表示方法

筏架彈性變形是相對而言的。外界擾動作用下筏架產生的實際位移包含“剛體位移”和“彈性變形位移”，兩者相互耦合，難以完全分離。因此，研究筏架彈性變形問題時，必須選擇一個合適的參考基準。

通常，氣囊控制系統將筏架四角高度作為筏架姿態平衡的控制參數，會優先將其位移控制在精度指標范圍內，所以將1#～4#傳感器位移作為筏架彈性變形的參考基準。

5#，6#傳感器處筏架的彈性變形位移可用其實際位置到參考基準的距離表示，如圖3所示。

圖3 筏架彈性變形表示方法Fig.3 Expression method of elastic deformation of raft

以5#位移傳感器為例，該處筏架彈性變形位移Δx5可表示為

(6)

式中，x1，x3，x5分別為1#，3#和5#位移傳感器讀數。

2.2 控制性能指標函數

大型筏架由于設備工況多，局部載荷變化大，導致筏架彈性形態復雜，難以通過氣囊壓力調整使所有位移參數同時收斂。

為避免系統振蕩甚至不收斂，在控制性能指標函數Hs中引入動態權重系數a，以提高控制算法對筏架不同彈性形態的適應性。筏架姿態及變形控制性能指標函數Hs可定義為

(7)

式中： |xj|為各位移傳感器讀數的絕對值，反映了筏架偏離理想姿態位置的大小；a為動態權重系數，用于提高控制算法對復雜工況的適應性，初始值為1，取值范圍為[0,1]；ε為筏架控制精度，由于ε關于筏架理想姿態位置對稱分布，所以式(7)中取ε/2。

顯然，當Hs<1時，筏架在控制精度ε范圍內，此時算法收斂。反之，若Hs>1并且最近兩次筏架調整效果不明顯，表明調整氣囊壓力已經難以改善筏架姿態及彈性變形，此時需要減小a值使筏架快速收斂，避免系統振蕩。

3 筏架姿態及彈性變形控制算法

3.1 主控制器設計

筏架姿態及彈性變形控制原理如圖4所示。假定控制系統將進行第k+1次調整，其調整步驟如下：

圖4 筏架姿態及彈性變形控制原理圖Fig.4 Flow diagram of attitude and elastic deformation control for raft

步驟1判斷動態權重系數a是否需要調整。以第k次調整后各位移傳感器參數變化量絕對值的最大值表示第k次筏架的調整效果

(8)

步驟2判斷氣囊是否需要調整。若Hs<1則表明筏架在控制精度指標ε范圍內，此時不需要調整氣囊；反之，進行下一步。

步驟3選擇需要調整的氣囊編號。

步驟4根據模糊控制規則確定氣囊充放氣時間。

步驟5預判筏架調整效果。

步驟6對筏架姿態和彈性變形進行調整。

3.2 氣囊選擇策略及預判

假設筏架處于理想姿態位置時，各位移傳感器讀數為0并且各氣囊均處于額定狀態，則氣囊高度偏差也可以反映筏架偏離理想姿態位置的大小。

以氣囊額定工作高度為零點，當筏架偏離理想姿態位置時，氣囊高度偏差為

Δh=h-H

(9)

式中： Δh為氣囊高度偏差，可由筏上各位移傳感器參數線性差值得到；h為氣囊實際工作高度；H為氣囊額定高度。顯然，當筏架位于理想姿態位置上方時，Δh為正值；反之，Δh為負值。

大型筏架姿態和彈性變形控制的實質是通過調整氣囊壓力來減小氣囊的高度偏差。但大型浮筏氣囊數量多，氣囊工作高度之間的耦合作用也較強，所以對某個氣囊進行充、放氣操作時，筏架其他位置氣囊的工作高度也發生變化，如圖5所示。

圖5 氣囊耦合作用的影響Fig.5 Influence of air spring coupling

顯然，充氣過程中，若兩個氣囊的高度偏差Δh相同，則控制系統應當優先對其中壓力較小的氣囊實施充氣操作；而放氣過程中，若氣囊高度偏差Δh相同，則控制系統應當優先對其中壓力較大的氣囊進行放氣。

因此，可以利用氣囊壓力參數對氣囊高度偏差進行定性識別，以減小氣囊耦合作用的影響。

(10)

圖5展示了筏架剛體假設條件下氣囊耦合作用的影響，然而大型筏架柔性較大，其彈性變形復雜，大大增加了氣囊調整時其他氣囊高度偏差變化的復雜性，可能會使筏架不收斂。

因此，為提高氣囊調整的準確性，需要對筏架調整效果進行預判，并根據預判結果對氣囊編號選擇進行修正。引入修正系數χ，得到氣囊編號選擇判據為

Qi=λi·χi·Δhi

(11)

式中：Qi為氣囊廣義高度偏差，用于判斷氣囊調整的優先級，Qi絕對值越大，則氣囊調整優先級就越高；λi為通過識別氣囊壓力參數得到的修正系數，用于減小氣囊耦合作用的影響；χi為根據筏架預判結果得到的修正系數，用于提高氣囊編號選擇的準確性，χi初始值為1，取值范圍為[0,1]； Δhi為氣囊高度偏差。

根據式(11)選擇優先級最大的氣囊進行調整，然后由模糊控制規則表確定氣囊充放氣時間，最后依據式(5)預判筏架的響應位移。

定義判據Jy來表示筏架調整是否有效

(12)

顯然，不論充氣還是放氣過程，當兩者符號相反，即Jy<0時，表明此次調整有效； 反之，需要減小χi重新選擇氣囊編號。根據試驗平臺系統調試結果，取χi的減小幅值為0.2。氣囊編號選擇及預判流程如圖6所示。

圖6 氣囊選擇及預判流程圖Fig.6 Flow diagram of air spring selection and prediction

4 試驗研究

本文試驗裝置為某船舶大型浮筏氣囊隔振裝置2∶1縮比試驗平臺，如圖7所示。其中，筏架尺寸為5.5 m×3.5 m×0.2 m；沿筏架兩舷側均勻布置20個氣囊隔振器；另布置6個位移傳感器，位置分布與圖2相同；通過一套液壓伺服加載裝置調整浮筏載荷。

圖7 浮筏氣囊隔振裝置試驗平臺Fig.7 Floating raft air spring isolation device test platform

根據相關技術標準，取筏架姿態及彈性變形控制精度ε為-1～+1 mm。試驗前手動調整氣囊使筏架偏離平衡位置約±3 mm，然后分別采用剛體浮筏控制算法和本文控制算法對筏架進行調整。

其中，剛體浮筏控制算法主要通過筏架四角高度控制筏架姿態平衡，控制目標是將1#～4#位移傳感器參數控制在精度指標范圍內；而本文控制算法是在控制筏架姿態平衡的基礎上盡可能地抑制筏架的彈性變形，控制目標是盡量將1#～6#位移傳感器參數同時控制在精度指標范圍內。

充氣調整過程試驗結果如圖8所示，調整后筏架彈性變形位移如表1所示。

圖8 筏架調整試驗曲線Fig.8 Raft adjustment test curve

表1 筏架彈性變形位移試驗值Tab.1 Test values of elastic deformation displacement of raft mm

從圖8和表1可知，采用剛體浮筏控制算法時，經14次調整，筏架姿態可被控制到-1～+1 mm，此時筏架最大變形位移為1.75 mm；采用本文控制算法時，經13次調整，筏架姿態可被控制到-1～+1 mm，再經過2次調整，筏架姿態可被控制到-0.5～+0.5 mm，調整后筏架最大變形位移為0.74 mm。對比可知，充氣調整時，本文控制算法能有效抑制筏架彈性變形，并且具有較高的控制精度。

放氣調整過程試驗結果如圖9所示，調整后筏架彈性變形位移如表2所示。

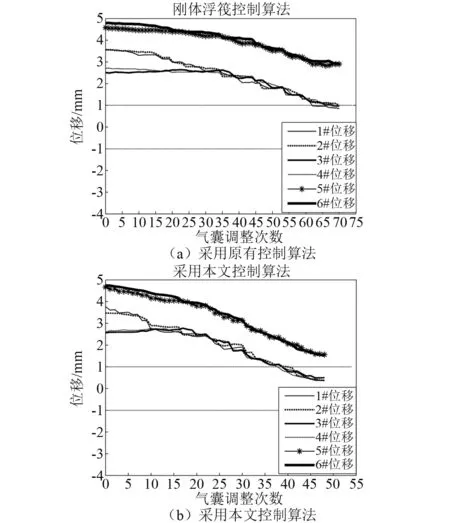
圖9 筏架調整試驗曲線Fig.9 Raft adjustment test curve

表2 筏架彈性變形位移試驗值Tab.2 Test values of elastic deformation displacement of raft mm

從圖9和表2可知，采用剛體浮筏控制算法時，經70次調整，筏架姿態可被控制到-1～+1 mm，此時筏架最大變形位移為1.99 mm；采用本文控制算法時，經50次調整，筏架姿態即可被控制到-1～+1 mm，調整后筏架最大變形位移為1.16 mm。對比可知，放氣調整時，本文控制算法調整速度較快，并且能有效抑制筏架彈性變形。

綜上，試驗結果表明本文控制算法不僅可以控制筏架姿態平衡，還能夠有效抑制筏架彈性變形，并且控制精度較高。

5 結 論

本文研究了大型浮筏氣囊隔振系統筏架姿態和彈性變形的控制問題。針對大型浮筏的特點，建立了柔性筏架響應模型并用于預判筏架的調整效果，同時提出了一種基于氣囊壓力參數識別的控制方法，并將筏架預判結果融入到該控制方法中，實現了大型浮筏姿態和彈性變形的自動控制。試驗結果表明：該控制方法可以控制筏架姿態平衡并有效抑制筏架彈性變形，同時還具有較高的控制精度。