計及運動副間隙的雙曲柄六桿壓力機機構動力學仿真向量鍵合圖法

王中雙， 尹久政

(齊齊哈爾大學 機電工程學院，黑龍江 齊齊哈爾 161006)

平面多體系統在工業生產中應用十分廣泛[1-3]，雙曲柄六桿壓力機機構是典型的該類系統，其低速鍛沖和急回特性十分突出，具有較高的推廣應用價值。然而，多體系統構件的實際加工及裝配均會產生誤差，所導致的運動副間隙會引發設備運行中的沖擊、振動及噪聲問題，給其性能及工作壽命帶來不利的影響。因此，計及運動副間隙的平面多體系統動力學研究一直是學術界關注的熱點問題[4-7]。現有的運動副間隙碰撞模型多數是以Hertz理論為基礎，但在機構實際運動過程中，Hertz定律的假設條件并不能始終得到滿足，這會對間隙接觸碰撞力描述的準確程度產生影響。為此，文獻[8]基于L-N(Lankarani-Nikravesh)碰撞力模型及改進彈性基礎模型，提出了一種修正的運動副間隙連續碰撞力混合模型，實際應用中能夠更精確地描述運動副間隙。

上述模型的建立方法是以分析力學及彈性力學為基礎，對于計及運動副間隙的多種能量形式并存的系統(例如：電機驅動的雙曲柄六桿壓力機機構系統)，不能用統一的方式實現系統動力學的建模，這在很大程度上制約了該類系統的動力學自動建模與仿真。鍵合圖法[9]從理論上可以有效地解決該類問題，但對于復雜的平面多體系統(例如:計及運動副間隙的雙曲柄六桿壓力機機構系統)，其標量鍵合圖模型的表達方式過于繁雜，實用價值有限。文獻[10]將標量鍵合圖的概念進一步擴展，提出了向量鍵合圖法。不僅可以用統一的方式實現多能域并存系統的建模，還具有表達方式簡明、建模過程程式化的特點，對于復雜多體系統動力學計算機建模與仿真問題的研究頗具特色及潛力。

文獻[11]基于向量鍵合圖方法，推導出便于計算機建模的系統驅動力矩及運動副約束反力方程，建立了三角形肘桿壓力機機構的向量鍵合圖模型，實現了其動力學自動建模與動態靜力計算。文獻[12]闡述了以廣義位移、廣義速度向量為關鍵向量的平面連桿機構向量鍵合圖模型的建立方法，應用相應的算法，在計算機上自動建立了RRR-RRP型平面六連桿壓力機機構驅動力矩方程，揭示了脈沖載荷作用下的機構驅動力矩變化規律。文獻[13]基于向量鍵合圖的基本概念，推導出便于計算機自動建立的系統狀態方程及運動副約束反力方程的統一公式，實現了計及驅動電機在內的3-RRR型平面并聯機器人機構系統動力學計算機建模及仿真，其方法特別適用于多種能量形式并存系統的動力學統一化建模及仿真問題。

上述以向量鍵合圖法為基礎的研究工作，均未有涉及到計及運動副間隙的機構動力學問題。文獻[14]基于二狀態非連續接觸運動副間隙模型，建立了考慮運動副間隙的平面四連桿機構向量鍵合圖，對其動態特性進行了分析。由于所建立的機構向量鍵合圖模型存在微分因果關系，使其建立機構動力學方程的過程局限于手工推導。文獻[15]以MLSD(massless-link/spring-damper)運動副間隙模型為基礎，建立了含轉動副間隙的RRR-RRP六連桿壓力機機構的向量鍵合圖模型，實現了其計算機自動建模及動力學仿真。但是，其在精確程度及實用性方面具有局限性。

為此，本文基于白爭鋒的研究所提出的修正非線性連續接觸碰撞力混合模型，推導出間隙運動副的相對碰撞速度向量方程，建立了更加精確描述運動副間隙的向量鍵合圖模型，具有通用性強、模塊化的特點，便于嵌入到系統的向量鍵合圖模型中。在此基礎上，建立了計及驅動電機、運動副間隙的雙曲柄六桿壓力機機構向量鍵合圖模型。應用王中雙等所述算法，實現了機構的計算機建模及動力學仿真。通過對仿真結果的分析討論，揭示了運動副間隙對雙曲柄六桿壓力機機構刀具的加速度及運動副約束反力的影響，驗證了所述方法的可靠性及有效性。通過與無質量彈簧阻尼運動副間隙模型的計算對比，進一步表明本文方法可以提高系統動力學仿真的精度及實用性。

1 修正非線性連續接觸碰撞力混合間隙向量鍵合圖模型

圖1為修正非線性連續接觸碰撞力混合間隙模型簡圖，構件Fi為軸套；構件Fj為軸；OFi，OFj分別為軸套和軸的軸心點；RFi，RFj分別為軸套和軸的半徑；rFOi，rFOj分別為軸套、軸的軸心點在全局坐標系OXY中的位置向量；δFi，δFj分別為軸套、軸的碰撞點在全局坐標系OXY中的位置向量；e為軸與軸套的偏心向量，其表達式為

圖1 修正非線性連續接觸碰撞力混合模型簡圖Fig.1 An improved hybrid nonlinear continuous contact and collision model

e=rFOj-rFOi

(1)

設δF為軸與軸套相互碰撞的壓入深度向量，相應的壓入深度δF為

δF=e-c

(2)

式中：c=RFi-RFj，為軸與軸套的半徑差；e為軸與軸套的偏心量。

在白爭鋒的研究基礎上，間隙運動副的連續接觸碰撞力可以進一步歸納成如式(3)向量形式

(3)

(4)

(5)

由圖1可得向量δF，δFi，δFj間的關系式為

δF=Sn(δF)(δFj-δFi)

(6)

對式(6)兩邊求導得

(7)

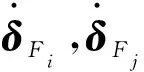
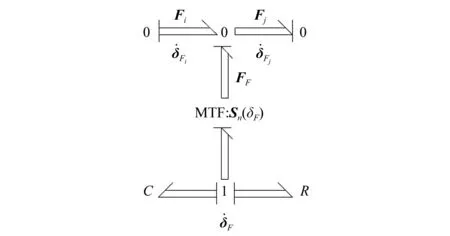
圖2 間隙轉動副向量鍵合圖模型Fig.2 A vector bond graph model with joint clearance

Behzadipour等和王中雙等的研究詳細闡述了平面多體系統向量鍵合圖模型的建立方法，將圖2所示間隙轉動副向量鍵合圖模型嵌入到系統向量鍵合圖模型的相應處，便可以建立計及運動副間隙的平面多體系統向量鍵合圖模型，這為該類系統的計算機建模與仿真奠定了重要基礎，下面通過仿真實例對此具體予以說明。

2 計及運動副間隙的雙曲柄六桿壓力機機構向量鍵合圖模型

由王中雙和等的研究可建立該系統永磁式直流驅動電動機的鍵合圖模型，如圖4(a)所示。由圖3可以看出，該機構是由通用曲柄滑塊壓力機的曲柄和傳動軸之間串聯一個雙曲柄機構所構成，曲柄AB、連桿BC、曲柄CDE、機架及連桿EF彼此間用轉動副連接，滑塊(刀具)與機架通過移動副連接。由于機構運行時滑塊(刀具)沖切工件會發生碰撞與沖擊， 轉動副F受實際沖切力的影響最直接，極易產生磨損，故這里僅計及轉動副F的間隙。應用Behzadipour等研究所述方法，可以分別建立圖3所示機構各構件的向量鍵合圖模型，將其按照機構的上述運動約束關系鍵接起來，可以建立計及運動副間隙的雙曲柄六桿壓力機機構向量鍵合圖模型，將其與圖4(a)驅動電機的鍵合圖模型進一步鍵接，可以建立圖3所示系統完整的向量鍵合圖模型，如圖4所示。其中，間隙轉動副F的向量鍵合圖模型如圖4(b)所示。

圖3 電機驅動含運動副間隙的雙曲柄六桿壓力機機構Fig.3 Double crank six-bar press mechanism with joint clearance driven by motor

通過上述方法所建立的機構向量鍵合圖模型，同時具有積分因果關系及微分因果關系，直接應用現有的方法進行機構的計算機建模及動力學仿真，代數上的處理非常困難。為此，將該機構各運動副約束反力向量Se5(轉動副B)、Se8(轉動副C)、Se10(轉動副D)、Se12(轉動副E)作為未知勢源向量，添加在圖4相應的0-結處，可以完全消除微分因果關系。如此建立的如圖4所示的機構向量鍵合圖，所有貯能元件皆具有積分因果關系，可以直接應用王中雙等所述方法實現機構的計算機建模與動力學仿真。

3 計及運動副間隙的雙曲柄六桿壓力機機構動力學仿真

由王中雙等所述方法知，與圖4所示系統向量鍵合圖相對應的系統獨立貯能場獨立運動的能量變量向量為

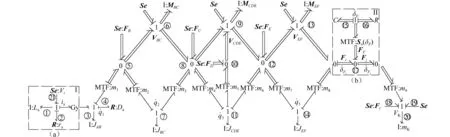
圖4 系統向量鍵合圖模型Fig.4 Vector bond graph model of system

(8)

式中，pi(i=1,3,7,11,14)為圖2中相應慣性元件的廣義動量。

系統獨立貯能場非獨立運動的能量變量向量

(9)

式中，pix，piy(i=6,9,13)為圖4中相應慣性元件的廣義動量向量在X軸及Y軸方向的投影；p20為圖4中相應慣性元件的廣義動量；VBCx，VBCy，VCDEx，VCDEy，VEFx，VEFy分別為相應構件質心速度向量在X軸及Y軸方向的投影；q15x，q15y為圖4相應容性元件的廣義位移δF在X軸及Y軸方向的投影。

相應的共能量變量向量

[VBCxVBCyVCDExVCDEyVEFxVEFyFFxFFyVK]T

(10)

式中：fi(i=1,3,7,11,14,20)為圖4相應慣性元件的流變量；e15x，e15y為圖4相應容性元件的勢變量向量在X軸及Y軸方向的投影；fix，fiy(i=6,9,13)為圖4相應慣性元件的流變量向量在X軸及Y軸方向的投影。

耗散場輸入、輸出向量分別為

(11)

(12)

式中：ei，fi(i=2,4)分別為圖4相應阻性元件的勢變量和流變量；e16x，e16y，f16x，f16y分別為圖4相應阻性元件的勢向量和流向量在X軸及Y軸方向的投影。

系統已知勢源向量

U1=[Se21Se6xSe6ySe9xSe9ySe13xSe13ySe18Se19]T=

[Vt0-mBCg0-mCDEg0-mEFgFr-mKg]T

(13)

式中，Seix，Seiy(i=6,9,13)分別為圖4相應勢源向量在X軸及Y軸方向的投影；Se1，Se18，Se19分別為圖4相應的勢源。

系統未知勢源向量

U2=[Se5xSe5ySe8xSe8ySe10xSe10ySe12xSe12y]T=
[FBxFByFCxFCyFDxFDyFExFEy]T

(14)

式中：Seix，Seiy(i=5,8, 10,12)分別為圖4相應勢源向量在X軸及Y軸方向的投影；FBx，FBy，FCx，FCy，FDx，FDy，FEx，FEy分別為運動副B、C、D、E約束反力向量在X軸及Y軸方向的投影。

應用王中雙等所述方法，由圖4可以建立向量Xi1與向量Zi1之間的關系矩陣Fi1、向量Xi2與向量Zi2之間的關系矩陣Fi2、向量Dout與向量Din之間的關系矩陣R。同時，可以建立與圖4所示系統向量鍵合圖模型相對應的結型結構矩陣。

將系統狀態變量向量Xi1，Xi2的初值、系統的結構參數、已知勢源向量U1、矩陣Fi1，Fi2，R及結型結構矩陣代入以王中雙等所述算法為基礎所編制的MATLAB軟件中去，可以用程式化的方式自動建立形式為一階非線性微分方程組的系統狀態方程并求解，部分仿真結果曲線如圖5～圖7所示。值得說明的是本文所采用的求解器Ode45，其基礎算法是變步長Runge-Kutta-Felhberg方法，適用于對精度要求較高的問題，是實際工程中應用較多的有效算法。

對圖3所示機構各構件進行受力分析，應用牛頓-歐拉法可以分別建立各運動構件質心加速度與所受外力的關系方程(既牛頓方程)及各構件角加速度與其所受力矩的關系方程(既歐拉方程)，將所得到的二階微分方程組形式的牛頓-歐拉動力學方程進一步降階整理并與驅動電機的動力學方程聯立，可以得到以Xi1，Xi2為狀態變量向量的一階非線性常微分方程組，這在形式上與用本文方法所得到的系統動力學方程是完全一致的。在MATLAB環境下，選用與本文上述方法同樣的求解器、設定同樣的參數求解，部分計算結果如表1、表2所示，與本文方法所得結果是完全一致的。將表1、表2所列數據用涂黑的圓點表示在圖5～圖7中，這些圓點均在對應的仿真曲線上，更加直觀地表明了這一點。但是，這一驗證過程手工處理量較大，相當繁瑣。相比而言，本文所述方法可以用統一的方式使該機電系統的動力學建模、仿真及分析過程以程式化的方式由計算機來完成，提高了該類工作的效率及可靠性。

表1 無間隙機構牛頓-歐拉動力學方法部分計算結果Tab.1 Some results without clearance calculated by Newton-Euler dynamic method

圖5 轉動副F約束反力合力Fig.5 Resultant constraint force of joint F

圖6 滑塊(刀具)加速度曲線Fig.6 Acceleration of slider (cutter)

圖7 轉動副E約束反力合力Fig.7 Resultant constraint force of joint E

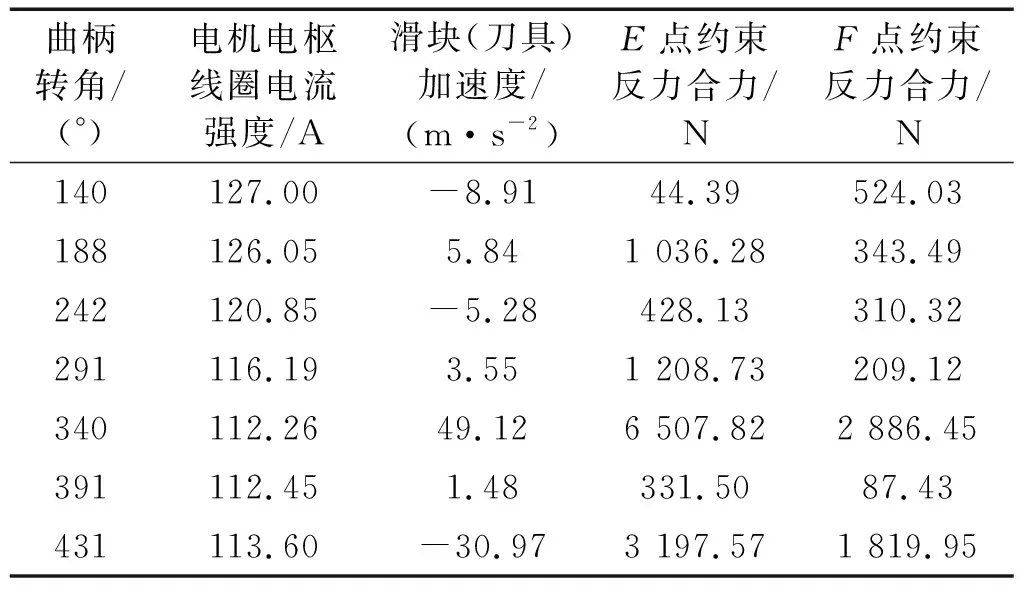
表2 有間隙機構牛頓-歐拉動力學方法部分計算結果Tab.2 Some results with clearance calculated by Newton-Euler dynamic method

圖5～圖7中，曲柄角位移的初值為87°(對應刀具上極限位置)。曲柄由該位置逆時針轉360°，機構完成一個運動周期。在機構一個工作循環中，對應無間隙機構的動力學仿真曲線均比較光滑。間隙使運動副軸與軸套間產生脈沖式的間隙碰撞力，導致間隙轉動副F的約束反力曲線、刀具加速度曲線及無間隙轉動副E的約束反力曲線均呈高頻振蕩狀態，在初始點附近表現得尤為明顯。另外，轉動副F的間隙使其本身的約束反力、(刀具)加速度及轉動副E約束反力的最大峰值均顯著增大。相比無間隙機構，有間隙機構相應仿真曲線的總體變化趨勢相近。具體分析如下：

由圖5知，曲柄角位移q1=334°時，無間隙機構轉動副F的約束反力最大峰值為2 821.41 N，角位移q1=336°時，有間隙機構轉動副F的約束反力最大峰值為3 329.14 N，其最大峰值增加了507.73 N，兩者達到最大峰值曲柄角位移相差2°。

由圖6知，當曲柄角位移q1=334°時，無間隙機構刀具加速度的最大峰值為47.54 m·s-2，當角位移q1=336°，含間隙機構刀具加速度的最大峰值為55.66 m·s-2，其最大峰值增加了8.12 m·s-2，兩者達到最大峰值曲柄角位移相差2°。

由圖7知，當曲柄角位移q1=334°時，無間隙機構轉動副E約束反力的最大峰值為5 757.34 N，角位移q1=336°時，有間隙機構轉動副E約束反力的最大峰值為6 622.33 N，其最大峰值增加了864.99 N，兩者達到最大峰值曲柄角位移相差2°。

由此可見，相比無間隙機構，含間隙機構刀具的加速度及運動副約束反力達到最大峰值時曲柄角位移相差均較小。間隙轉動副F本身的約束反力、刀具的加速度及轉動副E的約束反力對間隙均十分敏感，最大峰值分別增加了18%，17%，15%。其中，間隙轉動副F約束反力最大峰值的增長率尤為突出。這會導致壓力機機構的實際運行產生較大的沖擊、振動及噪聲，加劇運動副的磨損，給機構運動的穩定性、零部件的強度及工作壽命均帶來不利的影響。

針對本文的機電系統，應用王中雙等所述方法，將基于MLSD運動副間隙模型的向量鍵合圖嵌入到本文機電系統的向量鍵合圖模型中，可以建立計及MLSD間隙模型的系統向量鍵合圖模型。在此基礎上，采用王中雙等研究中MLSD模型的物理參數值，應用與本文同樣的建模方法(詳見王中雙等的研究)實現系統的動力學建模與仿真，其仿真結果曲線如圖8～圖10所示。

通過與圖5～圖7對比分析可知，兩種方法所得到的間隙轉動副F約束反力曲線、刀具加速度曲線及無間隙轉動副E約束反力曲線總體變化趨勢相近。在曲柄轉動的初始階段，均呈現高頻波動狀態。但是，隨著曲柄角位移的增大，圖8～圖10所示仿真曲線的波動頻率均有所下降，明顯低于圖5～圖7相對應的仿真曲線。圖8所示間隙轉動副F約束反力曲線的最大值為3 630.61 N，比圖5相應曲線的最大值增加了301.47 N；圖9所示刀具加速度曲線的最大值為71.23 N，比圖6相應曲線的最大值增加了15.58 N；圖10所示轉動副E約束反力曲線的最大值為7 053.29 N，比圖7相應曲線的最大值增加了430.96 N。由此可見，基于MLSD運動副間隙模型所得到的間隙轉動副F約束反力、刀具加速度及轉動副E約束反力的最大值均有所增加。進一步對比分析可知，圖8～圖10與圖5～圖7相對應的仿真曲線取得最大值的時間也皆不相同。

圖8 MLSD模型轉動副F約束反力合力Fig.8 Resultant constraint force of joint F based on MLSD model

圖9 MLSD模型機構滑塊(刀具)加速度曲線Fig.9 Acceleration of slider (cutter) based on MLSD model

圖10 MLSD模型轉動副E約束反力合力Fig.10 Resultant constraint force of joint E based on MLSD model

導致上述兩種方法仿真結果出現偏差的主要原因在于機構運行時，其間隙運動副軸與軸套間的碰撞是復雜的非線性過程，MLSD模型是用線性彈簧阻尼描述運動副間隙的彈性及阻性效應，不能真實反映運動副軸與軸套間碰撞過程中的非線性特性。另外，實際應用中準確地給出彈簧阻尼器的彈性系數及阻尼系數比較困難，本文所采用的MLSD模型的具體參數是通過直接引用白爭鋒和王中雙等的研究來獲得，這也是導致其仿真結果產生誤差的重要原因。相比較而言，本文所建立的模型是用非線性彈簧阻尼描述運動副間隙的彈性及阻性效應，不但能夠描述碰撞過程中的能量轉換特性，還包含碰撞體本身的材料屬性、局部變形及碰撞速度等信息，比較真實客觀地反映了間隙運動副的碰撞過程，有效地解決了實際應用中碰撞剛度系數及阻尼系數取值較困難的問題，且不受間隙尺寸和恢復系數的限制。由此可見，應用本文所建立的修正非線性連續接觸碰撞力混合間隙向量鍵合圖模型，可以進一步地提高計及運動副間隙的機電系統計算機建模及動力學仿真的精度及實用性。

4 結 論

(1)本文基于修正非線性連續接觸碰撞力混合間隙模型，推導出間隙運動副相對碰撞速度向量方程。在此基礎上所建立的間隙轉動副向量鍵合圖模型，可以用簡明的圖形方式更精細地描述運動副間隙，具有通用性強、模塊化的特點，便于嵌入到平面多體系統向量鍵合圖模型中，為更精確地實現計及運動副間隙的多能域系統計算機建模、動力學仿真及分析奠定了重要基礎。

(2)建立了計及驅動電機、運動副間隙的雙曲柄六桿壓力機機構向量鍵合圖，實現了其計算機統一建模及動力學仿真。驗證對比分析表明：本文所述方法是可靠的，進一步提高了系統動力學仿真的精度及實用性，其程式化的建模方式提高了計及運動副間隙的機電系統動力學建模、仿真及分析工作的效率。

(3)通過對具體實例的仿真結果分析，揭示了運動副間隙對電機驅動的雙曲柄六桿壓力機機構刀具的加速度、運動副約束反力的影響，對于機構的設計、控制及可靠性問題的研究具有一定的價值。

(4)本文工作為同類問題的研究提供了特色鮮明的新途徑，進一步拓展了向量鍵合圖理論及應用的研究領域。