核電廠主蒸汽管道阻尼減振與抗震分析

鄭成成，陳永祁，鄭久建，馬良喆

（1.燕山大學建筑工程與力學學院，秦皇島 066004；2.北京奇太振控科技發展有限公司，北京 100037）

眾所周知，核電在整個能源領域中占據著重要地位，各地擬建和在建的核電廠不斷增加，但工程建設中的管道振動問題一直存在。長期處于振動狀態下的管道系統（特別是在接管、測量計及法蘭等部位）很容易出現疲勞損傷，受交變應力的影響容易出現焊縫開裂的現象。這些問題會影響正常工作甚至會引發爆炸、火災等［1］，從而會造成巨大的生命和財產損失。福島核事故后，世界各國對核工程抗震安全性的要求更加嚴格，如何控制管道振動也成為行業研究的重點。管內流體的脈動、與管道相連機械的旋轉振動、水錘的沖擊作用以及地震荷載和風荷載等是引起管道振動的主要原因［1］。工程上用來控制管道振動的方法有：改造管道結構以及為管道增設支架、緩沖器等減振組件［1］。本文主要研究在正弦波激勵和地震荷載下的管道響應，并針對核電廠主蒸汽管道的振動情況及抗震需求，從增加管道系統阻尼的角度出發［2］，探究阻尼器在解決核電廠管道系統振動問題上的應用效果。

1 管道振動研究現狀

1.1 管道振動數學模型

管道的受迫振動主要是由作用在其上的周期性激振力引起的。這種周期性激振力除來自外部的地震荷載外，還主要來自管道內部的脈動壓力。當管道系統的固有頻率等于或靠近振源頻率時，會出現共振現象。通過有限元分析建立的管道振動方程如下［3，4］：

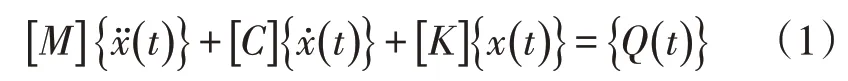
式中：［M］——管系的總質量矩陣；

［C］——管系的總阻尼矩陣；

［K］——管系的總剛度矩陣；

{Q(t)}——荷載向量；

{x(t)}——管系質點的位移列向量。

1.2 周期激振力下穩態響應［3，4］

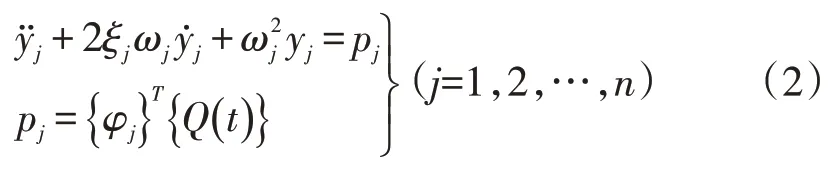
式中：ξj——第j階模態阻尼；

{φj} ——第j階模態矩陣；

yj——第j階振動幅值；

ωj——第j階模態固有頻率；

Pj——第j階主激振力。

用傅里葉級數將Pj展開得：

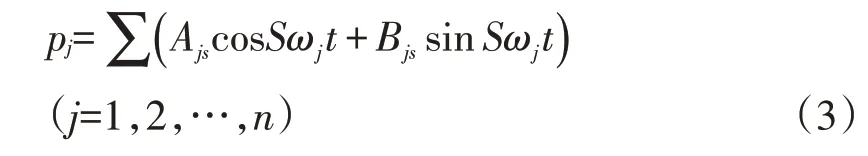
從式（3）可以看出，Ajs和Bjs及ωj是影響管道系統振動大小的主要參數，即激振力與管道內氣流脈動的大小和管系的設計有關。

1.3 管道系統的振動響應分析方法

目前，世界各國對管系在塑性變形下的破壞機理及地震動力反應都沒有進行深入研究［5］，大多數的管系減振、抗震分析都是以線彈性為基礎。等效靜力法、響應譜法以及動力時程分析法是目前常用的三種分析方法［5，6］。本文主要利用動力時程法進行管道減振及抗震分析。

1.4 對直管的研究［3，4，7，8］

早期研究的管道是厚壁的等直細長管，內部是無粘、可壓縮穩定流動的流體。在分析時用梁模型模擬管道系統，在不考慮結構阻尼、重力、流體壓力效應和外部拉壓力影響的前提下，等直管的方程可表示為：

式中：EI——管道抗彎剛度；

M——流體的線密度；

m——管道系統的線密度；

U——流體的平均流速；

ω——管道的橫向位移；

x——管道的軸線坐標；

t——時間變量。

早期，Paidoussis 和Issid 在方程（4）的基礎上建立了一個更為普遍的方程，重力、拉壓載荷及管道的材料阻尼等因素被考慮在內。方程的形式為：

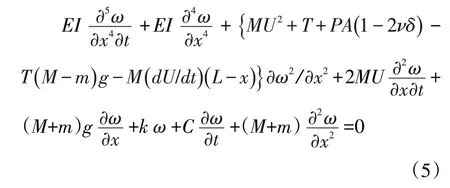
式中：E——材料內阻系數；

C——粘性阻力系數；

K——基礎彈性模量；

δ——管端能否軸向移動的因子，其取值非1即0；

ν——泊松比；

P——管內靜壓力；

T——軸向外載。

到目前為止，該公式是大家公認的描述流體管道液彈耦合振動較為完善的方程。

2 振動原因分析［9］

導致管道系統產生振動的激振力按來源可分為系統內部產生的激振力和系統外部產生的激振力兩類。系統內部產生的激振力主要來源于機械結構系統和流體系統，除了與管道連接的其他機械工作時產生的振動會引起管道振動外，對于輸送蒸汽的專用管道，由于蒸汽輸入口與出口存在一定的壓強差，快速流動的蒸汽會引發管道振動。系統外部產生的激振力主要來源于附近工作的其他機械設備及風、地震等自然力。究其根源，共振仍是引起管道振動的主要原因，當管道結構固有頻率中某階頻率處于動力設備激勵力頻率的共振范圍之內時［（0.8～1.2）f］就會發生氣柱共振或機械共振，使管道產生劇烈振動。

3 管道阻尼器耗能減振原理［10，11］

本文中管道減振所用設備是一種預存內壓的液體黏滯阻尼器，主要由外部缸體、帶有小孔的活塞、活塞桿、流體阻尼介質以及密封裝置和連接裝置等組成［12］。減振原理是阻尼介質阻礙活塞相對缸體作往復運動時產生阻尼力。阻尼力的計算式為：

式中：F——阻尼器的阻尼力；

C——阻尼器的阻尼系數；

α——速度指數；

V——阻尼器活塞與外殼的相對運動速度。

由式（6）可知，該阻尼器產生的阻尼力與剛度無關，只與速度有關。與結構運動方向相反的阻尼力將振動產生的動能轉化為熱能耗散掉，可以達到控制管道振動的目的。

4 案例分析

本文研究的核電廠主蒸汽管道是一段長約11.2 m 的直管道，外徑965 mm，厚度44 mm，材質為SA335 P11。為防止蒸汽管道升溫時由于熱伸長或溫度應力而引起的管道變形或破壞，需在管道上設置多種補償器，來減小管壁的應力和作用在閥門或支架結構上的作用力［13，14］。整個管道系統包括直管道以及支座、支吊架等零部件。

本次研究主要分為正弦波荷載作用下的管道阻尼減振分析和地震動作用下的阻尼抗震分析。目的就是分析在不同激振力作用下，阻尼器的減振和抗震效果。

4.1 阻尼減振分析

本文用正弦波激勵模擬管道正常工作時受到的激振力擾動。這種激振力的特點是持續時間長，呈周期性，且伴隨著管道系統工作的整個生命周期。傳統控制管道振動的方法是設置剛性支架，通過增大系統的剛度來減小管道的振動。事實證明，這種方法雖然在一定程度上能減小管道振動，但容易在支撐處產生應力集中，導致局部變形過大，產生疲勞破壞。而阻尼器通過給管道提供附加阻尼，消耗管道的振動動能，不會產生剛度［15］。

4.1.1 模態分析

為比較設置阻尼器和使用普通剛性支架對管道振動的影響，本文利用Sap2000建立管道有限元模型，并在模型中相應節點處施加約束與支撐剛度，進行模態分析，得到蒸汽管道前6階振動特性參數（見表1）和前4階振型形狀（如圖1所示）。

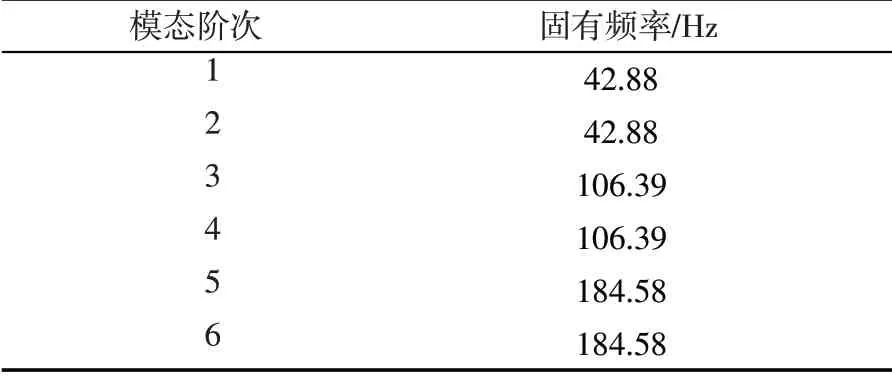
表1 蒸汽管道系統前6階固有頻率Table 1 The first 6 natural frequencies of the steam piping system

從表1 和圖1 可以看出，管道結構振型具有如下特點：（1）直管道的自振頻率較大；（2）結構第1 階振型固有頻率為42.88 Hz，表現為直管道一階對稱橫彎；（3）結構第2階振型固有頻率與1階振型相同，但表現為直管道一階對稱豎彎；（4）結構第3 階振型固有頻率為106.39 Hz，表現為直管道一階反對稱橫彎；（5）結構第4 階振型固有頻率與第3階振型相同，但表現為直管道一階反對稱豎彎。從自振模態看，直管道主要以橫彎和豎彎為主，所以應采取措施控制管道的橫向振動和豎向振動。

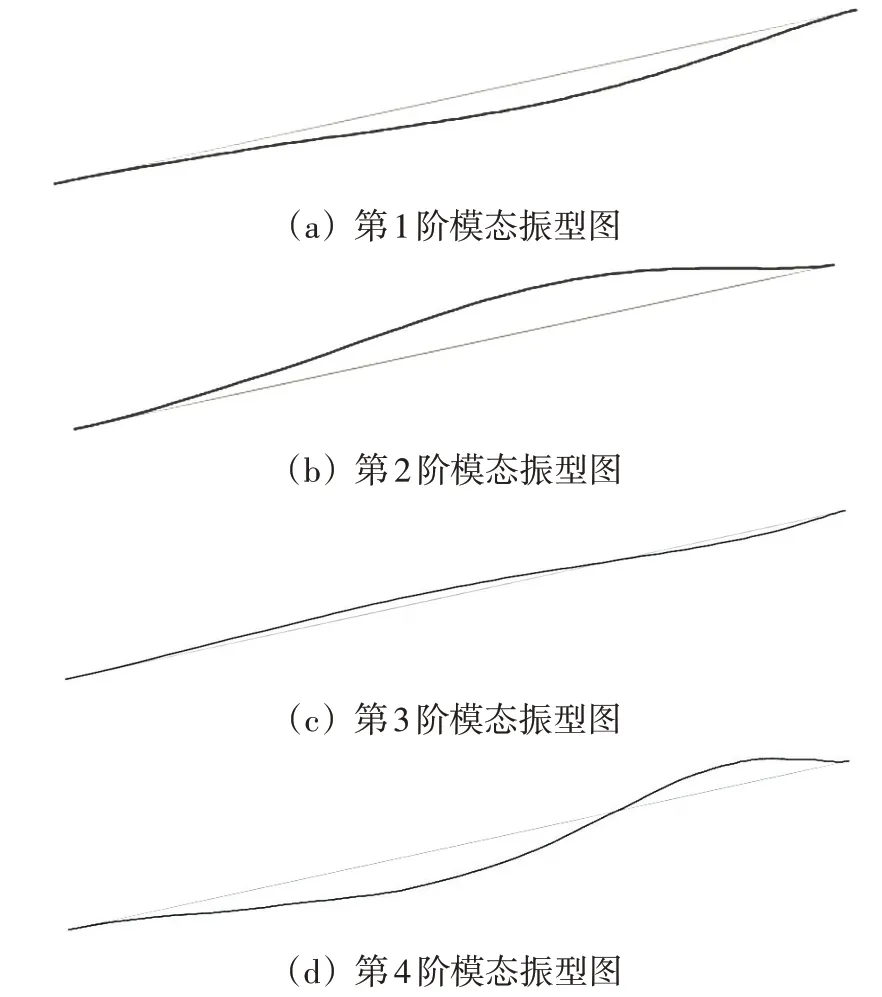
圖1 前4階模態振型圖Fig.1 The first four modes of mode shape

4.1.2 動力時程分析

本文通過對設有剛性支撐（支架）和黏滯阻尼器的管道模型分別輸入正弦波時程激勵，計算出管道上各質點隨正弦波振動的位移和速度，具體剛性支撐和阻尼器的設置方式如圖2所示。

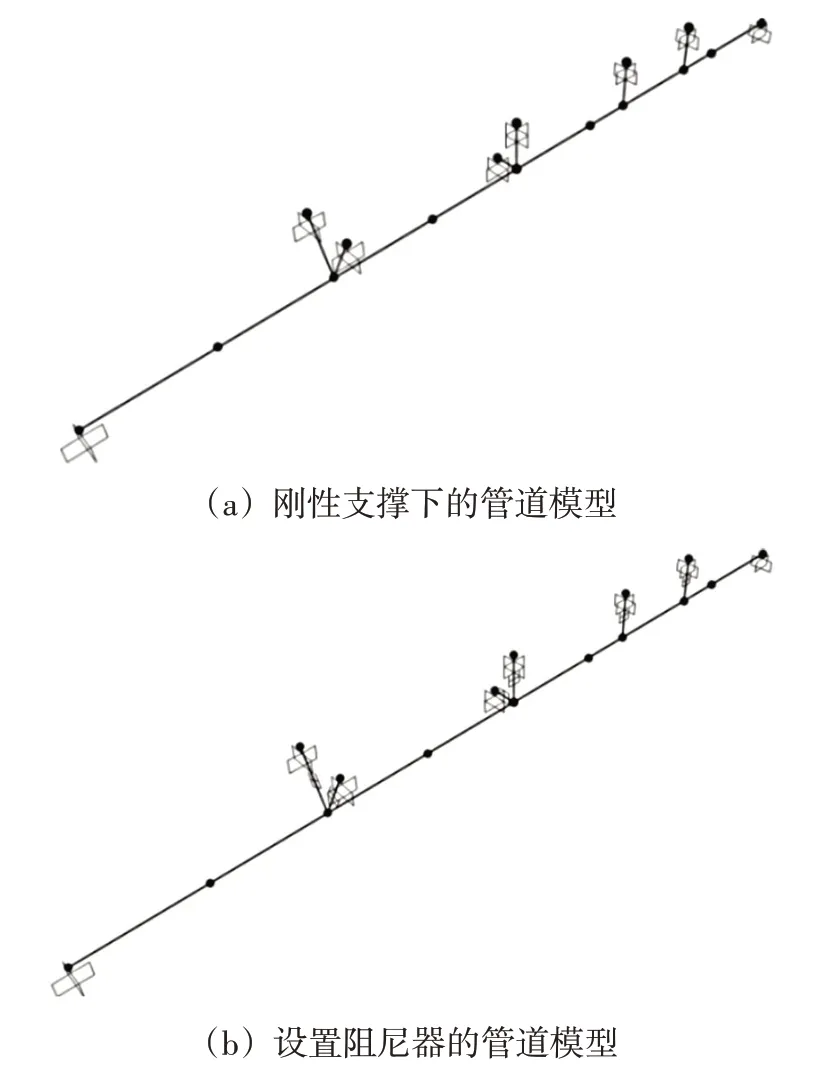
圖2 采用剛性支撐和設置阻尼器的管道模型Fig.2 Pipe model with rigid support and damper

正弦波時程函數所參考的正弦函數方程為：

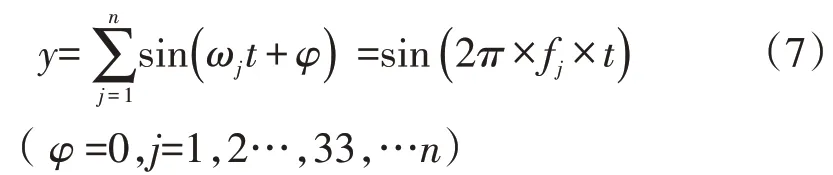
管道動力特性分析結果表明，橫向和豎向振動較為明顯，因此本文通過對管道輸入橫向和豎向振動頻率為33 Hz 的正弦波荷載進行分析，正弦波時程函數曲線如圖3所示。

圖3 正弦波時程函數曲線Fig.3 Sine wave time history function curve

本文為了比較采用剛性支撐和設置阻尼器兩種工況下管道的減振效果，分別在采用普通剛性支撐（支架）和設置阻尼器的管道模型上每隔2.8 m選取一個節點作為測試點，共取4個。阻尼器參數取值：阻尼系數C=500 kN/（m/s）0.2，阻尼指數α=0.2。

本文通過時程分析分別計算出管道每個測試點在兩種減振措施下的振動位移和速度，如表2和表3所示（限于篇幅，本文僅給出橫向激勵下的結果）。圖4和圖5分別是2號測點采用剛性支撐與設置阻尼器的管道振動位移和振動速度時程曲線對比。

表2 剛性支撐和阻尼器下管道節點振動位移對比Table 2 Comparison of vibration displacement of pipe joints under rigid support and damper

從表2 和表3 可以看出，與采用普通剛性支撐（支架）相比，設置阻尼器后管道在激振力作用下的振動位移和振動速度均明顯減小，振動位移減振率均在36%以上，振動速度減振率均在73%以上，振動控制效果明顯。圖4和圖5則反映出，在管道整個振動時程內阻尼器都正常工作，振動位移和振動速度得到了有效控制。

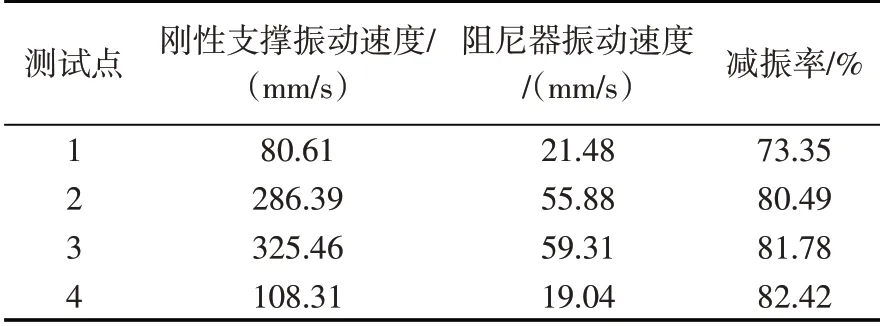
表3 剛性支撐和阻尼器下管道節點振動速度對比Table 3 Comparison of vibration speed of pipe joints under rigid support and damper

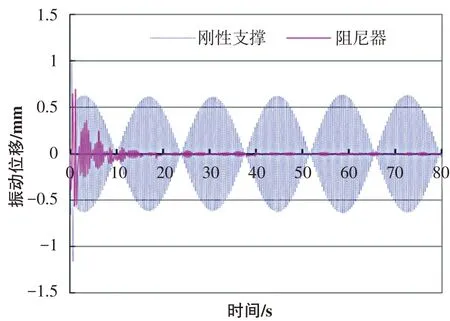
圖4 2號測點在剛性支撐與阻尼器下振動位移時程曲線對比Fig.4 Comparisonoftime-historycurvesof vibrationdisplacementofNo.2measuring pointunderrigidsupportanddamper

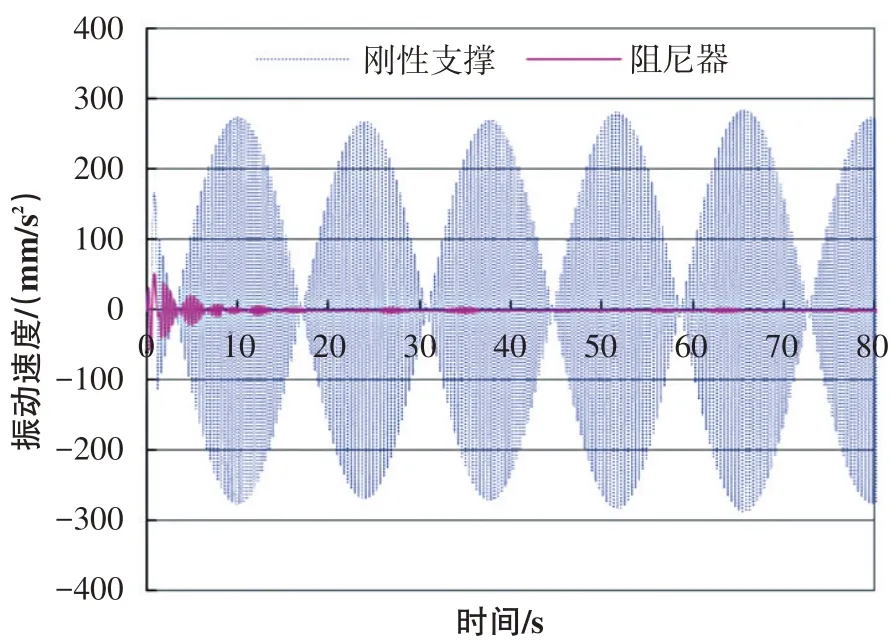
圖5 2號測點在剛性支撐與阻尼器下振動速度時程曲線對比Fig.5 Comparison of the time-history curve of the vibration speed of the No.2 measuring point under rigid support and damper

在正弦波荷載激勵下，設置剛性支撐與阻尼器的管道固定端所受剪力和彎矩情況如表4和表5所示。

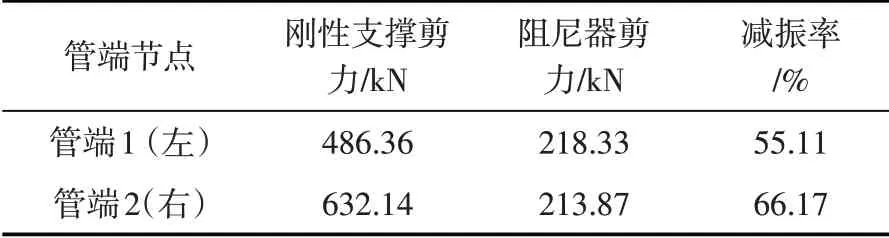
表4 管道固定端所受剪力對比Table 4 Shear force comparison of fixed ends of pipes

從表4 和表5 可以看出，在橫向激振力作用下，設置阻尼器的管道固定端所受彎矩和剪力均小于采用剛性支撐的管道，剪力最大減振率在66%左右，彎矩最大減振率在55%左右。可見阻尼器能有效降低管端受力，抑制疲勞破壞。

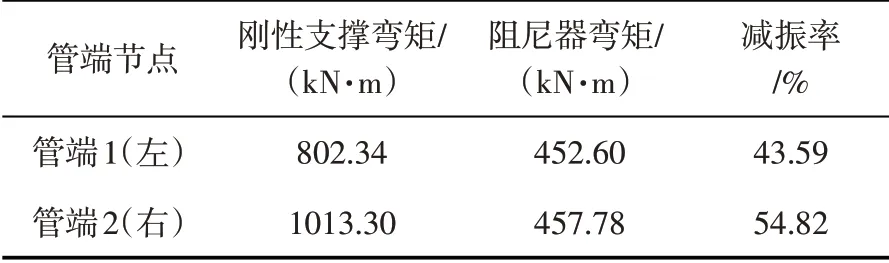
表5 管道固定端所受彎矩對比Table 5 Comparison of bending moments of fixed ends of pipes

此外，時程分析還輸出了在正弦波激勵下6個不同位置阻尼器的出力情況，見表6。

表6 阻尼器最大出力Table 6 Maximum output of damper

從表6 可知，在橫向正弦波激勵下位于管道中段的3 號阻尼器（橫向設置）出力最大，而豎向設置的5號和6號阻尼器出力相對較小。不同部位阻尼器的出力情況可作為選取阻尼器型號和安裝位置的依據。在本文案例中，可選取150 kN的阻尼器來滿足管道的減振需求。

4.2 阻尼抗震分析

4.2.1 模態分析

通過模態分析得出的蒸汽管道系統前6階振動特性參數如表7 所示，管道有限元模型如圖6所示。

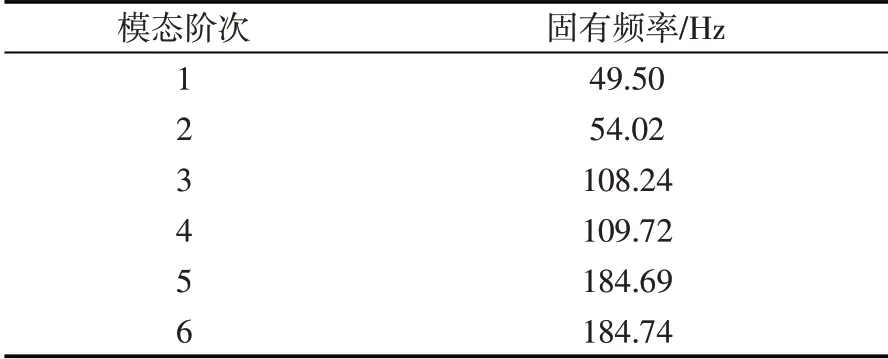
表7 管道前6階固有頻率Table 7 The first 6 natural frequencies of the pipeline

圖6 有限元管道模型Fig.6 Finite element pipeline model

圖7是通過模態分析得到的管道采用普通支撐的前4階模態振型圖。

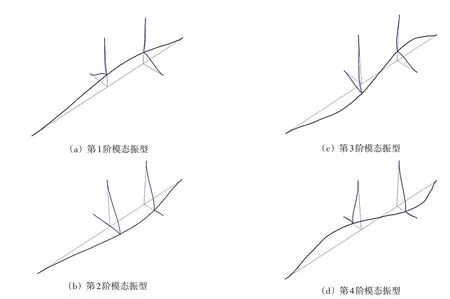
圖7 管道前4階模態振型圖Fig.7 The first 4 order mode shapes of the pipeline

從前4階的振型圖可以看出，蒸汽管道的第1階振型為Z 向的對稱彎曲，第二階振型為Y 向的對稱彎曲，第三階管系發生扭轉，表現為反對稱豎彎，第四階表現為反對稱橫彎。結構的振型圖按照Y 向平動、Z 向平動以及X 向扭轉的規律相互交替出現［5］。因此，管道抗震應以控制Y、Z 向的平動和X向的扭轉為主。

4.2.2 動力時程分析

為了對比管道在未設置阻尼器和設置阻尼器兩種工況下的抗震情況，本文在模態分析的基礎上進行動力時程分析，計算管道在地震荷載下的響應。計算中采用三種不同的地震波形，地震波形1 由擬合反應譜而來；地震波形2 由ELCen?tro波改造而來；地震波形3由TAFT波改造而來，如圖8所示。三者的最大加速度峰值均為35cm/s2。阻尼器的阻尼系數C=100 kN/（m/s）0.2，阻尼指數α=0.2。圖9是管道阻尼器安裝示意圖。

圖8 地震波形3時程曲線Fig.8 Seismic waveform 3 time history curve

圖9 阻尼器安裝示意圖Fig.9 Dampers installation diagram

具體的對比方案為：分別在有無阻尼器管道模型上取3、4、5、6號節點作為測試點，編號分別為1、2、3、4，共4個。利用動力時程分析得到在三種不同地震波形下各個節點的振動位移和振動速度。

圖10 和圖11 分別給出了地震波形3 下管道系統有無阻尼器的振動位移和振動速度對比結果。圖12是地震波形3下4號測點加設阻尼器前后的振動位移時程曲線對比。

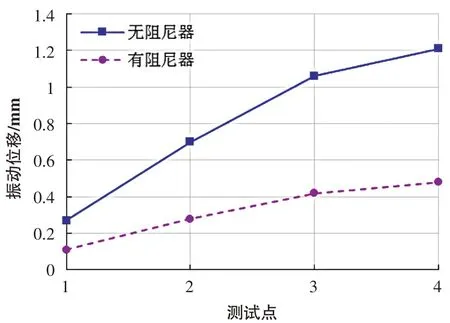
圖10 管道有無阻尼器振動位移對比Fig.10 Comparison of vibration displacement of pipeline with or without damper

從圖10 和圖11 中可以看出，加設阻尼器后，管道的振動位移和振動速度均明顯減小，振動位移最大減振率在60%左右，振動速度最大減振率在75%左右，對振動速度的控制效果顯著。圖12 反映出，在整個地震荷載作用過程中，阻尼器正常工作，起到了抑制管道位移振動的良好作用。

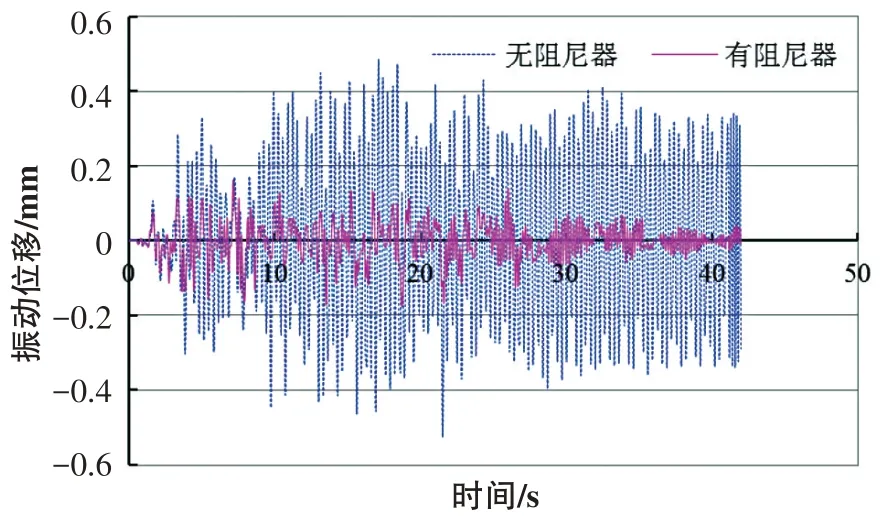
圖12 管道振動位移時程曲線對比Fig.12 Comparison of time-history curves of pipeline vibration displacement

本文通過時程分析，分別計算出在3 種橫向地震荷載作用下，蒸汽管道加設阻尼器前后兩端固定支座所受的剪力和彎矩，如圖13、圖14所示。

圖13 三種地震波下支座所受剪力對比Fig.13 Comparison of the shear forces of the three seismic waves under the support

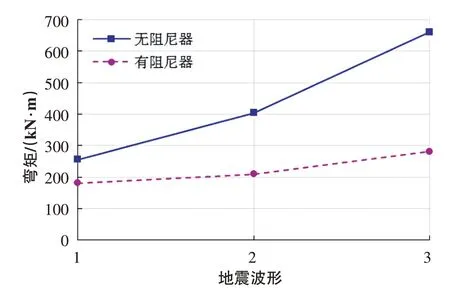
圖14 三種地震波下支座所受彎矩對比Fig.14 Comparison of bending moments of the bearings under three seismic waves

從圖13 和圖14 中可以看出，在三種不同地震荷載作用下，加設阻尼器后管道兩端所受的剪力和彎矩均減小，剪力最大減振率在55%左右，彎矩最大減振率在57%左右。結果證明，阻尼器能減弱地震荷載對兩端支座產生的作用力，能有效控制管道端部的變形。

從表8 可知，在三種地震荷載作用下單個阻尼器最大出力在35 kN 左右，具體阻尼器參數如表9所示。

表8 三種地震波下阻尼器最大出力Table 8 Maximum output of damper under three seismic waves

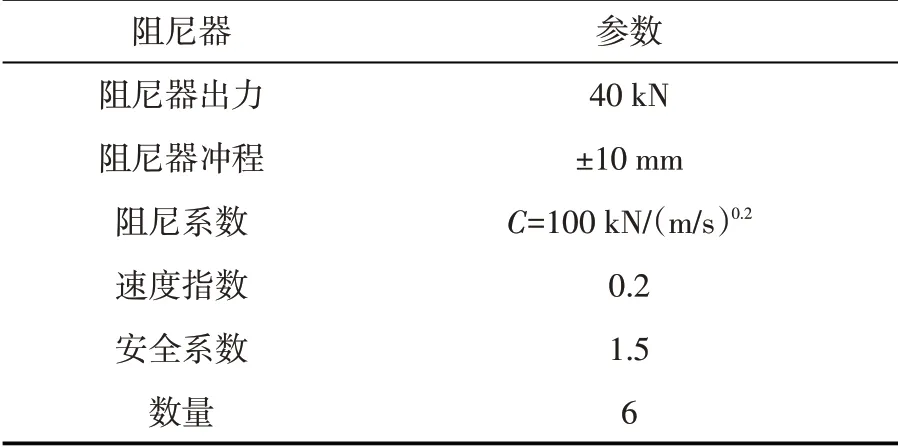
表9 阻尼器參數Table 9 Damper parameter

5 結論

本文從能量耗散的理論角度分析阻尼減振和抗震技術，結果表明:（1）受正弦波激勵的管道的振動位移和振動速度均小于采用剛性支撐的管道，其中位移最大減振率在54%左右，速度最大減振率在80%左右。且加設黏滯阻尼器后，管端所受剪力和彎矩也有所減小。說明黏滯阻尼器比普通剛性支撐更能有效控制管道振動。（2）受地震荷載作用的管道的振動位移和振動速度也明顯減小，其中位移最大減振率在60%左右，速度最大減振率在75%左右。且加設阻尼器后，管端支座處所受的剪力和彎矩均有所減小。說明黏滯阻尼器的使用不僅能有效控制管道在地震荷載作用下振動位移和振動速度，還能有效降低管端受力，減少疲勞荷載對管道的損害。（3）針對不同管道的減振與抗震需求，可采取不同的措施，而阻尼器作為一種消能減振的工具，無疑提供了一種更有效的減振方案。