基于ABAQUS 的超聲變幅桿設計及有限元分析
汪銳,王艷
(200093 上海市 上海理工大學 機械工程學院)
0 引言
超聲振動復合工藝是將傳統切削加工與超聲振動結合所形成的新型復合加工技術。超聲振動復合工藝可以有效降低切削力,減少刀具的磨損,提高加工效率,同時還拓展了難加工材料的應用領域[1]。超聲變幅桿是超聲振動系統中的重要部件,其主要作用是將換能器輸出的振動進行放大,達到需要的振幅,滿足超聲復合加工的要求[2]。本文通過理論計算設計了階梯形超聲變幅桿,并利用有限元分析軟件ABAQUS 對超聲變幅桿進行了模態分析及諧響應分析,驗證設計的合理性并進行了優化。
1 超聲變幅桿的理論計算
本文選擇45#鋼作為超聲變幅桿的材料,其具體材料參數如表1 所示。

表1 45#鋼材料參數Tab.1 Material parameters of 45# steel
超聲變幅桿的性能可以通過共振頻率、放大系數、形狀因數等很多參數來描述。其中,放大系數Mp是指變幅桿工作在共振頻率時輸出端與輸入端的質點位移或速度振幅的比值;形狀因數φ是衡量變幅桿能達到最大振動速度的指標之一,它僅與變幅桿的形狀有關,φ 越大,所能達到的最大振動速度也就越大[3]。如圖1 所示,本文設計的變幅桿類型為階梯形變幅桿。以階梯形變幅桿的軸線為x 軸建立坐標系,本文中假設不計機械損耗,且變幅桿截面上的應力分布是均勻的。在簡諧振動的條件下,變截面桿縱振動的波動方程為[3]

式中:ξ——質點位移函數;S——桿的橫截面積函數;k——圓波數,且k=ω/c,ω——圓頻率,c——縱波在變幅桿中的傳播速度。

圖1 階梯形變幅桿結構示意圖Fig.1 Structure schematic diagram of stepped horn
因階梯形變幅桿由兩端不同橫截面積的均勻桿組成,所以S 為常數,故式(1)可簡化為

對方程求解,可知質點位移函數為
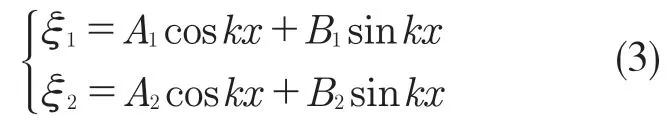
根據連續性可以得知邊界條件,進而求出A1,A2,B1,B2,并帶入式(3)得質點位移函數

式中:ξi——輸入的振動位移;ξo——輸出的振動位移;ZL——負載力阻抗;Z0=S1ρc;ρ——變幅桿的密度。當a=b=λ/4(為波長)時,位移節點x0=0,即變幅桿的中心位置。
在波節點等于零處,放大系數

根據實際要求,超聲變幅桿的大端直徑D1為71 mm,小端直徑D2為31 mm。選用超聲波發生器的工作頻率為20 kHz。根據上述式子,可以計算出階梯形變幅桿的參數,如表2 所示。

表2 階梯形變幅桿的參數Tab.2 Parameters of stepped ultrasonic horn
2 超聲變幅桿的有限元分析
2.1 超聲變幅桿的模態分析
模態分析主要用于計算某個結構件或零件的固有頻率和振型,是進行其他動力學分析如諧響應分析、瞬態動力學分析及譜分析的基礎[4],因此,應先對超聲變幅桿進行模態分析,確定其固有頻率等振動特性。
在動力學問題中,系統的平衡方程為

式中:[M]——質量矩陣;[C]——阻尼矩陣;[K]——剛度矩陣;{Q}——力矢量。
模態是一個機械系統的固有屬性,每一個模態都有一個對應的固有頻率、振型以及阻尼。模態分析動力學問題的方程為

變幅桿的模態分析中,結構的自由振動為簡諧振動,即

由式(10)可得變幅桿的固有頻率。應用有限元法對變幅桿進行分析,利用前面計算得到的尺寸參數,在ABAQUS 仿真軟件中進行三維實體建模,如圖2 所示。接著進行材料屬性的設置、創建線性攝動頻率分析步、輸出前20 階模態;布種、設置網格屬性最后劃分網格,如圖3 所示。

圖2 三維模型Fig.2 3D model

圖3 網格劃分示意圖Fig.3 Mesh diagram
最后提交分析,計算得到超聲變幅桿的模態分析結果。圖4 是該變幅桿第8 階到第11 階的模態振型云圖。由圖4 可知,在第8 階、第9 階模態下,變幅桿的小端發生了彎曲振動;第11階模態下,變幅桿整體都產生了彎曲振動,均不符合設計要求。第10 階模態下的振型滿足變幅桿縱向振動的要求,且此時振型的固有頻率為20 486 Hz,接近設計要求即超聲波發生器的輸出頻率20 kHz。
2.2 超聲變幅桿的諧響應分析
諧響應分析是用來分析線性結構在受到按簡諧規律變化的載荷時的穩態響應。一般諧響應分析有2 種求解方法:模態疊加法與完全法。采用模態疊加法必須先進行模態分析,提取出無阻尼的特征模態,通過變換得到一組模態坐標表示的單自由度運動方程,求解各個單自由度運動方程,并得到系統在模態坐標下的穩態響應,最后通過變換獲得系統在物理坐標下的穩態響應。而完全法則是通過對模型的原始方程直接積分計算[5]。本文采用模態疊加法求解,掃頻范圍設置為15~25 kHz。在變幅桿大端施加沿軸線方向大小為20 N 的簡諧載荷。
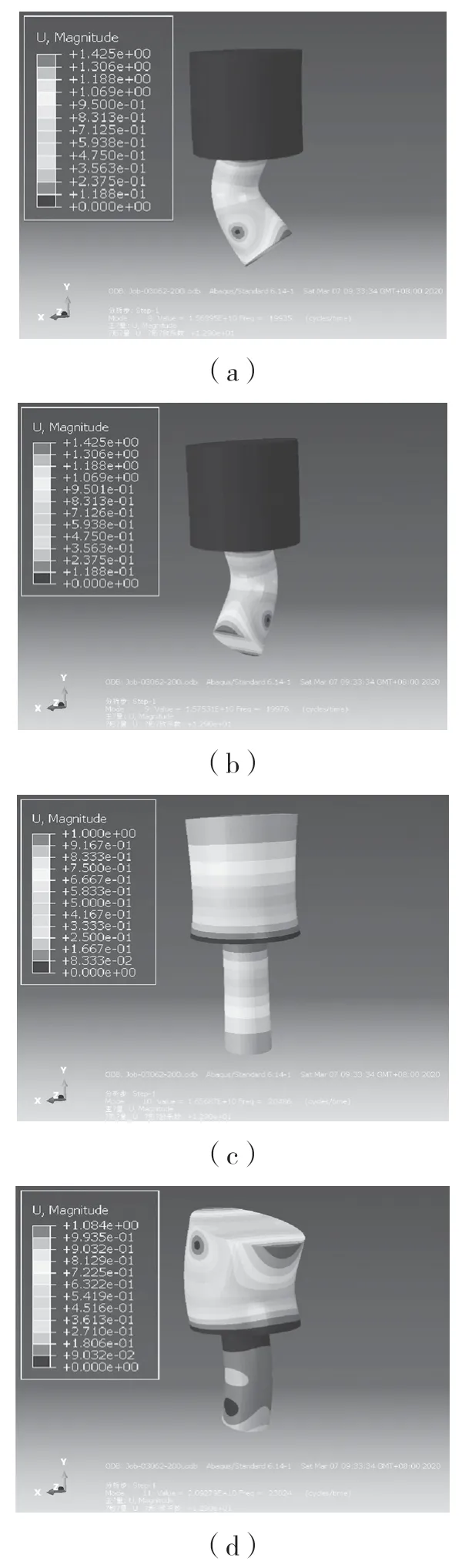
圖4 不同固有頻率下的模態振型圖Fig.4 Mode shapes at different natural frequencies
如圖5 所示,進行分析之后提取出頻率為20 486 Hz 的應變和應力云圖。可以看到,應力集中部位和應變集中部位均為大端與小端連接處,最大應力值為238.1 MPa,最大應變為6.0×10-4,使用過程中變幅桿容易因疲勞發生斷裂。現對變幅桿的結構進行優化。

圖5 階梯形變幅桿的應力及應變云圖Fig.5 Stress and strain cloud image of stepped horn
優化的主要手段為在截面突變處設計一段過渡圓弧[6]。需要注意的是,此時變幅桿結構已經發生改變,意味著固有頻率也會隨之發生改變,因此,需要重新進行模態分析,在做諧響應分析時,與前面的分析結果進行對比。在變幅桿大端和小端連接處增加一個半徑為10 mm 的圓弧。如圖6(a)所示,進行建模后,依照2.1 節所述進行模態分析,得到優化之后的變幅桿固有頻率為20 456 Hz,接著依照上文所述的諧響應分析步驟進行諧響應分析,得到的應力分布結果如圖6(b)所示。可以看到,變幅桿最大應力位置在圓弧與大端連接處,最大值108 MPa。
為了研究不同半徑的過渡圓弧對變幅桿的影響,再分別對過渡圓弧半徑為14,18 mm 的變幅桿進行模態分析,得到它們的固有頻率分別為20 507,20 651 Hz,接著進行諧響應分析,得到各自在其固有頻率下的應力云圖,最大應力分別為97.2,93.0 MPa。圖8(a)是不同圓弧半徑變幅桿固有頻率變化圖,圖8(b)是不同圓弧半徑變幅桿最大應力值的變化圖。從圖中可以看出,隨著圓弧半徑的增大,變幅桿的固有頻率逐漸增大,變幅桿最大應力位置向圓弧與變幅桿連接處轉移且最大值逐漸變小,說明增加過渡圓弧可以改善應力集中現象,進而降低疲勞效應提高使用壽命。

圖6 10 mm 半徑過渡圓弧的階梯形變幅桿Fig.6 Stepped horn with a transition arc of radius 10 mm

圖7 不同半徑過渡圓弧的變幅桿應力云圖Fig.7 Stress nephograms of variable horn with different transition arcs

圖8 不同圓弧半徑對變幅桿固有頻率及最大應力的影響Fig.8 Influence of different arc radius on natural frequency and maximum stress of horn
3 結語
超聲技術在實際生產中的應用越來越廣泛。作為超聲系統的重要部件之一,變幅桿的重要性不言而喻。本文以階梯形變幅桿為研究對象,利用設計參數對變幅桿進行了理論計算,得到了階梯形變幅桿的三維模型,接著對其進行模態分析,得到了符合縱振動特性的固有頻率,然后進行了諧響應分析。通過分析發現,階梯形變幅桿大端和小端連接處應力值最大,容易發生斷裂,故利用增加過渡圓弧的方法對變幅桿進行了優化。本文對不同半徑過渡圓弧對變幅桿的影響也作了分析,結果發現,隨著過渡圓弧半徑的增大,變幅桿的固有頻率逐漸增大,并且最大應力隨之減小,說明增加過渡圓弧可以有效改善應力集中問題,延長變幅桿使用壽命。

