“線性時間選擇算法”教學探討

張惠艷 陳芳

摘要：基于選擇問題的線性時間要求，本文從算法思想、算法實現以及算法復雜度三個部分對《算法設計與分析》課程中“線性時間選擇算法”的教學方法進行了探討，用圖形直觀地分析了線性時間選擇算法的時間復雜度的最好情況和最壞情況，便于學生理解和掌握。

關鍵詞：線性時間選擇算法; 二次取中法; 算法復雜度

中圖分類號：G642 ? ? ? ?文獻標識碼：A

文章編號：1009-3044（2021）35-0260-04

Discussion on the Teaching of Linear Time Selection Algorithm

ZHANG Hui-yan， CHEN Fang

（Huaiyin Normal University， Huaian 223300，China）

Abstract： Based on the linear time requirement of the selection problem， this paper discusses the teaching method of "linear time selection algorithm"in the course of algorithm design and analysis from three parts： algorithm idea， algorithm realization and algorithm complexity. It analyzes the best and worst situation of the time complexity of linear time selection algorithm intuitively with graph， which is convenient for students to understand and master.

Key words： linear time selection algorithm; median of medians rule; algorithm complexity

1引言

《算法設計與分析》是計算機科學與技術專業居于核心地位的專業課程，學生無論是考研究生還是從事IT方面的工作，掌握好這門課的算法理論和算法思想都是非常重要的。這門課不僅要學習基本算法理論，還要用程序設計語言來實現算法，以便學生更好地理解和掌握算法設計的基本方法和技術，有助于學生進一步學習計算機技術，適應更廣泛的職業挑戰。迄今為止，算法學家們設計了許多基本和經典的算法，如何將這些算法傳授給學生，讓學生熟練掌握并能運用所學知識解決實際問題，是教授這門學科的教師所面對的主要問題。

大部分高校選用的教材是陳慧楠《算法設計與分析》[1]第二版。教材的算法基本都給出了C++的代碼實現，便于學生很好地理解和掌握復雜抽象的算法設計理論。但本課程是一門理論性和實踐性都很強的課程，為了取得好的教學效果，很多授課老師都探討了該課的教學方法[2-8]，提出了自己的教學建議。本文從教學與實踐兩個環節針對該書的第五章“分治法”中的“線性時間選擇算法”談談教學體會。

線性時間選擇算法是在若干元素中不用排序方法求出其中第k小的方法，并且要求時間復雜度是線性的。文中采用了“二次取中法”并結合遞歸調用和快速排序的劃分思想得到了求第k小的線性時間選擇算法。

2 線性時間選擇算法的課堂教學

2.1算法描述

1）將S中元素5個一組分成n/5份，每份5個元素，若n不是5的整數倍，剩余元素在分組時不予考慮;

2）每5個一組，分別求出每組中間元素;并通過交換將所有中間值依次存放在序列的最前端;

3）求序列前端M的中間值m*;

4）以二次中間值m*為主元，進行劃分操作;

5）如果左子序列元素個數p=k，則k-1為第k小元素;如果左子序列元素個數p>k，則在左子表中繼續搜索，如果左子序列元素個數p<k，則在右子表中繼續搜索k-p小元素。

首先引導學生如何實現元素分組并將每組元素的中間值調到整個序列的最前端？在不排序的情況下如何求得前端序列的中間值？求得中間值后如何對序列進行劃分？劃分后如何找到要求的第k小元素？然后結合實例和C++代碼來詳細講解這一算法思想。

2.2算法實現

程序主要代碼段是select函數：

int select（int k， int left， int right， int r） ? //k是第幾小數，left為左下標，right為右下標，r為多少個元素一組

{ int n=right-left+1;

if （n <= r） ? //問題足夠小，返回下標

{ InsertSort（left，right）;

return left+k-1;

}

for （int i=1;i<=n/r; ++i）

{ InsertSort（left + （i - 1）*r，left+i*r-1）;

swap（a[left+i-1]， a[left+（i-1）*r+Ceil（r，2）-1]）; ? ?//將每組元素的中間值集中存放在子表前面

}

int j=select（Ceil（n/r， 2）， left， left+ n/r-1， r）; ? ?//n/r表明一個分了多少組，二次求中間值，其下標為j

swap（a[left]， a[j]）;

j = Partition（left， right）; ? ? ? ? ? ? //用二次取中值對原序列重新劃分

printfMoM（j）; ? ? ? ? ? ? ? ? ? ?//輸出二次取中值

if （k == j-left + 1）

return j;

else if （k < j-left + 1）

return select（k， left， j-1， r）; ? ? ?//左子表第K個元素

else

return select（k-（j-left +1）， j+1， right， r）; ? //右子表第k-（j-left+1）小元素

}

select函數中調用InsertSort排序函數，當序列規模不超過5個元素時，可以采用InsertSort排序直接求出第k小元素，并且一次取中值等于二次取中值;如果序列規模超過5個元素，則對序列循環調用InsertSort函數分組排序，并將每一組的中間值調到序列的最前端，可直接調用庫函數swap，再遞歸調用select函數求二次取中值。這里給相應的代碼都加上了注釋，理解起來更容易;swap函數中還調用了Ceil函數，功能相當于上取整，代碼如下：

int Ceil（int x，int y） ? ? ? ? ?//x，y均為整形數

{ if （x%y==0） return x/y;

else return x/y+1;

}

教材中沒有給出這個函數，可讓學生自己補充上取整函數;緊接著select函數遞歸調用自身，求得前端序列的中間值，并用這個中間值對整個序列進行劃分，即調用Partition函數。最后根據劃分的結果以及k值的大小，用if-else語句來選擇select函數，繼續遞歸調用，最終得到第k小的值。

2.3算法實例講解

教材中給了35個元素的求第7小的實例，對這個實例的運行講解可以很好地讓學生理解上述一系列提問。

步驟1：首先將給定的35個元素存入全局數組a：

int a[35]={41，76，55，19，59，63，12，47，67，45，26，76，74，33，18，65，86，49，77，35，80，53，19，97，22，52，62，39，60，59，29，72，31，56，91};并在主函數中通過賦值語句int j=select（7，0，34，5）調用select函數。

步驟2：進入select函數，首先調用InsertSort排序函數，代碼如下：

void InsertSort（int left， int right） ? ? //插入排序

{ for （int i=left+1; i<=right;++i） ? //從left+1開始進行插入，一直到right結束

{ int temp= a[i];

int j;

for （j=i-1; j>=left&&temp<a[j];j--）

{ a[j+1]=a[j]; ?}

a[j+1] = temp;

}

}

通過循環7次調用InsertSort排序函數，即依次調用InsertSort（0，4），InsertSort（5，9），InsertSort（10，14），InsertSort（15，19），InsertSort（20，24），InsertSort（25，29），InsertSort（30，34），將7組元素按從小到大的順序排序，并通過swap函數將每組序列的中間元素依次調至序列的最前端。此時可得到序列的最前端元素依次是55，47，33，65，53，59，56這七個元素。

步驟3：程序執行int j=select（Ceil（n/r，2），left，left+n/r-1，r）這條語句遞歸調用select函數自身，此處n=35，r=5，Ceil（n/r，2）=Ceil（35/5，2）=4，left=0，left+n/r=7傳遞給實參right，即運行select（4，0，6，5），即在前端序列的7個元素中找出第4小元素，這是select函數第一次遞歸調用自身。

步驟4：第二次進入select函數，因7除以5取整結果是1，所以只有第一組元素需要再排序，得結果33，47，53，55，65，通過swap（a[left]，a[j]）語句將53調至序列的最前端得前端序列為53，47，33，55，65，59，56，程序執行int j =Select（Ceil（n/r，2），left，left+n/r-1，r）; 即第三次遞歸調用select函數，求前端序列53，47，33，55，65的中間值，即執行select（1，0，0，5），直接返回0，完成此次遞歸調用。

調用printfMoM（j）輸出函數，代碼如下：

void printfMoM（int j）

{ cout << "二次取中值為：" <<a[j]<<endl;

for （int i=0;i<35;++i）

{ cout << a[i] << " ";

if （（i+1）%5==0）

cout << endl;

}

}

輸出結果“二次取中值為53”，這是第一次求得的“二次取中值”。

步驟5：執行j=Partition（left，right）;即調Partition函數，此處left=0，right=7，代碼如下：

int Partition（int left， int right） ? //劃分函數，返回分割點

{

int i = left; ? ?//以最左邊的數為分割點

int j = right + 1; ?//由于do while先執行--j，為了保證最右邊的數參與比較，所以先加一

do

{ do

{ ++i;

} while （a[i] < a[left]）;

do

{ --j;

} while （a[j] > a[left]）;

if （i < j）

swap（a[i]， a[j]）;

} while （i < j）;

swap（a[left]， a[j]）;

return j;

}

即用53對前端7個元素序列進行第一次劃分。得到劃分結果為33，47，53，55，65，59，56。此時元素53所對應的數組下標為2，即j=2;因為函數select（4，0，6，5）是要求前端序列得第4小元素，此時前端序列只有兩個元素，j=2<4，所以第4小元素應是右端序列的第一小元素。

步驟6：執行語句Select（k-（j-left+1），j+1，right，r），即第四次遞歸調用函數select（1，3，6，5），此時left=3，right=6，n=right-left+1=4，4<5，直接對右端序列55，65，59，56進行插入排序，得55，56，59，65，它的第1小元素即為55，運行結果是返回3，即j=3，因a[3]=55，得到第二次“二次取中值”55。

步驟7：執行swap（a[left]，a[j]）;將55調到序列的最前端，執行j=Partition（left，right）;此處left=0，right=34，即用55完成對原始序列的第一次劃分，并printfMoM（j）即輸出二次取中值55。

教材對二次取中值55如何得到的講解得不夠細，在得到“二次取中值”55時，程序已經在select（7，0，34，5）函數中遞歸調用select函數3次，分別是select（4，0，6，5），select（1，0，0，5）得第一次“二次取中值”并對前端序列進行劃分，其運行結果如圖1;select（1，3，6，5）得第二次“二次取中值”并對原始序列的劃分，其運行結果如圖2。圖中的紅色下劃線是后標注的，可以清楚地看到“二次取中值”在原序列中的位置。很多同學此處都理解得不夠透徹，這里給出了詳細的分析運行過程。

步驟8：因為j=17，j-0+1=18>k=7，left=0，故執行語句else if（k<j-left+1） return select（k，left，j-1，r）;即第五次調用函數select（7，0，16，5）。

步驟9：第五次進入select函數，首先調用InsertSort排序函數，此時共17個元素，5個元素一組，只需調用3次InsertSort函數，依次是：InsertSort（0，4），InsertSort（5，9），InsertSort（10，14），將3組元素按從小到大的順序排序，并通過swap函數將每組序列的中間元素依次調至序列的最前端。此時可得到序列的最前端元素依次是45，31，22，直接插入排序得22，31，45，前端序列共3個元素，求其中間元素，即第2小，遞歸調用select（2，0，2，5）得到j=1，第6次調用select函數結束，即第三次二次取中值31。用31對原序列的前17個元素進行劃分，運行結果如圖3所示。可看到劃分后31的下標是7，是前17個元素的第8小元素，因此第7小元素應在31的左端繼續找。

步驟10：因為j=7，j-0+1=8>k=7，left=0，故執行語句else if（k<j-left+1） return select（k，left，j-1，r）;即調用函數select（7，0，6，5）。

步驟11：第7次進入select函數，執行select（7，0，6，5）此時共7個元素，18，22，26，19，19，12，29。首先調用InsertSort排序函數，5個元素一組，只需1次調用InsertSort函數即InsertSort（0，4），得18，19，19，22，26，取中間值19，第八次調用select（1，0，0，5），得j=0，第八次遞歸調用結束，得到第四次二次取中值19，并通過swap函數將19調至序列的最前端。用19對這7個元素進行劃分，得18，12，19，22，26，19，29，運行結果如圖4所示。19的下標j=2，所以j-left+1=2-0+1=3，此時k =7>3，因此第7小元素應在a[2]=19的右側，執行return select（k-（j-left+1），j+1，right，r），即調用select（4，3，6，5）。

步驟12：第九次進入select函數，此時共4個元素，因此進行InsertSort排序，排序結果是19，22，26，29，調用結束返回select函數，執行return left+k-1，3+4-1=6，即返回下標6，selcet函數調用到此結束，回到主函數，j=6即29即為所求得第7小元素，程序到此運行結束。主函數如下：

int main（）

{

int j=select（7，0，35-1，5）;

cout <<"第七小的值為："<<a[j]<< endl;

return 0;

}

至此教材中選用的35個元素把selcet函數的每一條語句都執行了一次，主函數依次調用了select（7，0，34，5），select（4，0，6，5），select（1，0，0，5），select（1，3，6，5），select（7，0，16，5），select（2，0，2，5），select（7，0，6，5），select（1，0，0，5），select（4，3，6，5），select函數共被調用了9次。教材中此例的元素個數35和各元素的值以及求解第7小的設計都考慮得特別巧妙，這是一個值得所有學算法的學生好好學習的實例，可以很好地幫助學生理解程序的遞歸調用，提高學生的算法理解和實現能力。

3 線性時間選擇算法的復雜度分析

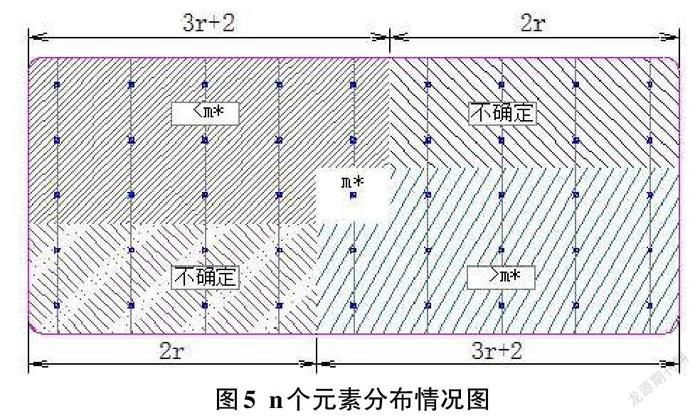
教材中給出了線性時間選擇算法的復雜度分析，但不夠直觀，這里結合圖形給出線性時間選擇算法的最好和最壞時間復雜度分析。n個元素（元素可重復），5個元素為一組，共分為n/5（最后的幾個元素可不考慮）每組按從小到大的順序排序，如圖5所示：

假設m*的左側有r列，右側有r列，則問題的規模：n=5（2r+1）=10r+5，子問題最壞情況：3r+2+2r+2r=7r+2;最好情況：3r+2+2r=5r+2，可以根據算法步驟分析得到問題最壞時間復雜度為：T（n）=T（n/5） +T（7/10n）+cn，用遞歸樹易得：T（n）=O（n）;最好時間復雜度為：T（n）=T（n/5）+T（1/2n）+cn，用遞歸樹易得：T（n）=O（n）;因此該算法具有線性時間復雜度。若3個元素一組是否能得到線性時間復雜度？7個元素一組呢？留給讀者考慮。

4 結語

線性時間選擇算法因為結合了元素的排序、劃分以及函數的遞歸調用，教師在講解以及學生在理解接受這一算法的過程中都有一定的難度，這里結合本人上課實際情況以及授課效果給出了一種易懂易掌握的方法，該方法收到了非常明顯的教學效果，激發了學生對算法學習的興趣。

參考文獻：

[1] 王曉東.算法設計與分析第二版[M].北京：清華大學出版社，2016.

[2] 畢方明，楊文嘉.算法與復雜度分析案例化教學改革[J].教育教學論壇，2018（44）：102-103.

[3] 南姣芬， 楊文雅， 李紅嬋，等. 《算法設計與分析》教學過程中的思考[J]. 教育現代化， 2019，6（35）：195-196.

[4] 袁李萌子， 周杰. 《算法分析與設計》課程教學初探[J]. 教育現代化， 2019，6（70）：89-90..

[5] 郭惠芳，劉寒冰.算法設計與分析課程研討教學的探索[J].計算機教育，2018（4）：60-62.

[6] 秦丹.算法設計與分析教學常見問題分析[J].電腦知識與技術，2014，10（24）：5719-5720.

[7] 季曉慧， 姚國清， 張玉清，等. 計算思維與實踐編程能力培養并重的算法設計與分析教學[J]. 電腦知識與技術：學術版， 2020，16（4）：70-71.

[8] 范昊，束德勤.《算法設計與分析》課程教學方法研究[J].教育教學論壇，2020（9）：246-247.

【通聯編輯：王力】