基于化學反應神經網絡的納米Al-PTFE復合體系反應動力學建模研究

許亞北，初慶釗，陳東平

(1.北京理工大學 爆炸科學與技術國家重點實驗室，北京 100081; 2.爆炸防護與應急處置技術教育部工程研究中心，北京 100081)

引 言

納米鋁-聚四氟乙烯(Al-PTFE)作為典型的活性復合材料，具有高能量密度、較好的力學性能和熱穩定性而得到了廣泛應用[1-4]。在納米鋁-聚四氟乙烯儲存過程中，熱分解與其安全性能息息相關[5]。因此，近年來Al-PTFE復合材料的熱分解特性研究得到了廣泛關注[6-10]。如WU Jia-xiang等[11-13]分析了鋁顆粒粒徑、溫度等因素對Al-PTFE復合材料的熱反應行為的影響，發現鋁顆粒尺寸和溫度均與反應密切相關。TAO Jun[14]利用密度泛函理論計算了PTFE的熱解產物與鋁的反應過程，并測試了Al-PTFE體系的反應壓力和溫度，發現分解產物與Al從898K開始發生反應。在文獻中則研究了其他物質(TiH2、Ni)、Al和PTFE含量對Al-PTFE的反應和動力學特性的影響[15-18]。雖然大量學者對這一體系的熱分解行為及反應機理進行了深入研究[4,8,9,19]，但由于Al-PTFE熱解本身是一個復雜的化學反應過程，涉及到多步反應路徑和大量的化學成分，目前對其化學動力學的理解還存在明顯的不足。

為深入理解含能材料的熱分解特性，需要開展熱分解動力學計算研究。在含能材料熱分解動力學計算方面，最常用的動力學模型為Kissinger[20]、Friedman[21]、Ozawa[22]和Starink[23]等方法。毛亮等[1]采用Starink法對納米Al-PTFE體系進行化學反應動力學計算，得出PTFE基Al活性材料的活化能為208.5kJ/mol。此方法忽略復雜體系的詳細反應機理，通過線性擬合得出表觀活化能。潘劍鋒[24]通過DSC對Al-PTFE反應材料進行線性升溫，發現其具有典型的動力學特征，由Kissinger方程計算得到Al/PTFE的活化能為309.1kJ/mol，此Kissinger法需要至少3種不同升溫速率的分解曲線，通過擬合分解峰溫得到活化能，并不能得到整個反應過程中的活化能變化趨勢。有些學者則采用Friedman和Ozawa動力學模型對RDX和HMX的熱分解進行計算，得到隨反應進度發生變化的活化能[25-26]。以上常用的動力學計算方法都是從幾條不同升溫速率的熱解曲線上同一轉化率的溫度計算活化能，不用假設反應機理函數，這些方法求解活化能相對較為快捷。但目前已有文獻中的熱解反應動力學模型均是基于一步式總包反應，并不能針對體系的每步反應進行動力學計算。詳細熱解反應動力學模型的建立需要開展大量針對性的實驗研究，其過程緩慢而復雜，對具體的化學結構和材料特性有明顯的依賴性，這在一定程度上阻礙了固體熱解反應動力學模型的發展。近年來，神經網絡模型逐漸應用到各種復雜體系的建模中。邢江寬等[27]采用神經網絡模型分析了生物質熱解動力學參數和生成物之間的關系，準確地預測了生物質的熱解產物和動力學參數。LUO Kun等[28]使用神經網絡模型準確預測了多種煤炭的熱解產物。但是以上研究都是基于人工神經網絡模型，缺乏真實的物理含義，無法闡明反應過程。化學反應神經網絡(CRNN)[29]利用神經網絡模型求解反應動力學方程，可以提出多步總包反應機理，能夠深入理解復雜復合體系的燃燒動力學行為。

為此，本研究首次將CRNN應用于納米Al-PTFE反應動力學建模過程中，開發一種既能擬合實驗數據，又能闡明反應路徑和動力學參數的神經網絡建模方法[30-34]。首先詳細介紹了CRNN框架，通過CRNN法對不同升溫速率的納米Al-PTFE熱重實驗數據進行學習；然后建立基于納米Al-PTFE化學反應神經網絡框架，并討論不同數量的反應路徑和生成物質對模型精度的影響；最后得出物質殘余質量分布、反應路徑和動力學參數(表觀活化能、指前因子) ，結合納米Al-PTFE的化學反應過程，對反應路徑和生成物質進行討論，預測納米Al-PTFE體系可能存在的反應機理。與許多其他數據驅動的建模方法相比，此CRNN模型不需要實驗樣品的具體性質，反應路徑(化學計量系數)和動力學速率常數都被視為可優化的參數，不需要對反應路徑的先驗知識[27]。該方法還可以擴展到其他含能材料，為其動力學模型開發提供一定借鑒及參考。

1 計算方法

1.1 化學反應神經網絡法(CRNN框架)

首先簡要介紹CRNN框架，并將Al-PTFE熱解的約束條件納入其框架。Al-PTFE復合物作為初始輸入物質，假設Sn為反應中間物質和生成物質，此處Sn不總代表一個物質，可以代表多個物質組分。Al-PTFE熱分解反應體系的反應方程式如下:

(1)

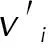
(2)

(3)

式中：參數A、n和Ea分別代表反應速率常數中的指前因子，非指數溫度依賴因子和活化能。進一步將每個中間體和產物的生成速率寫為：

(4)

單步反應的CRNN網絡和多步反應神經元網絡如圖1所示。

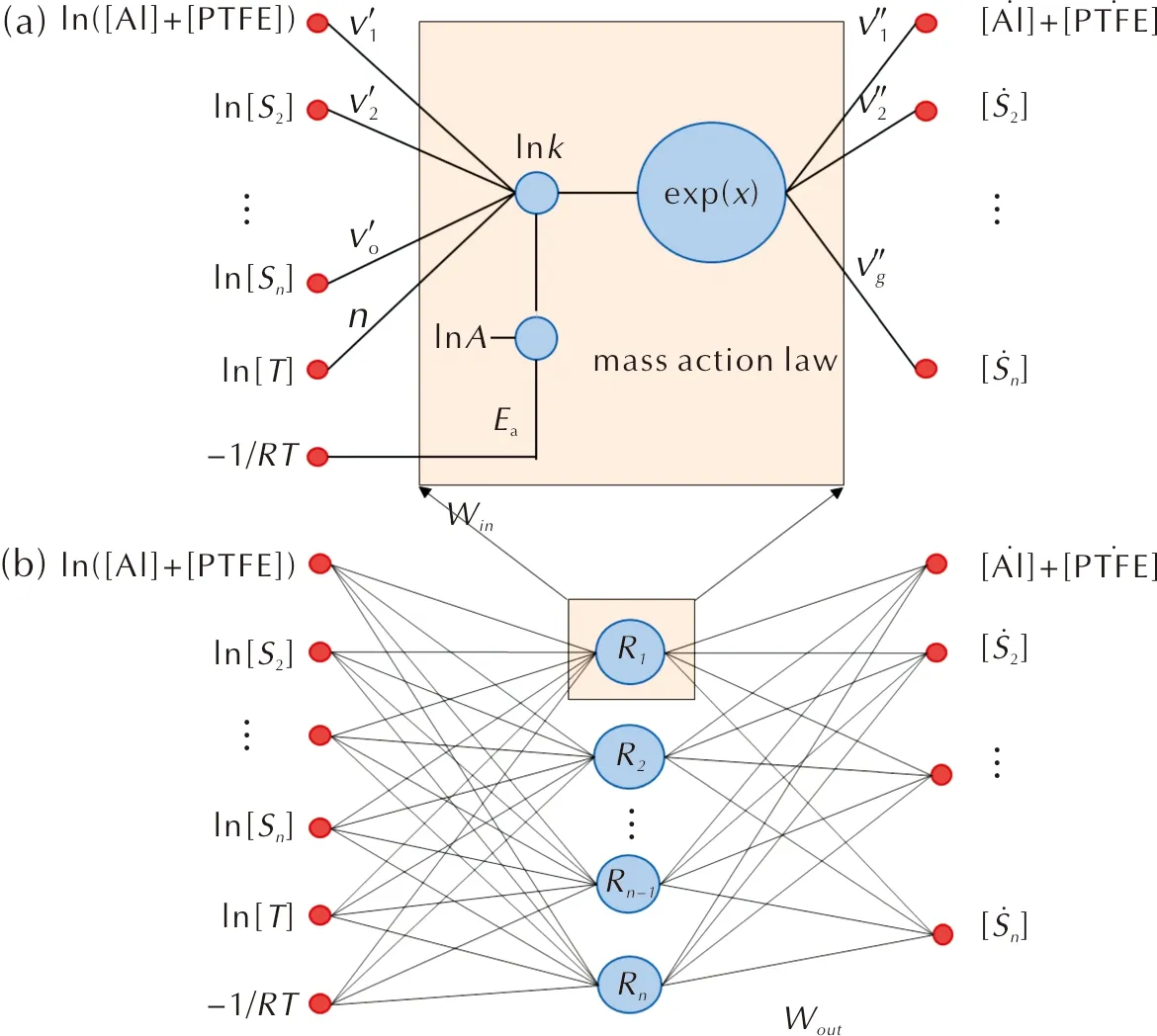
圖1 單步反應的CRNN網絡(a)和多步反應神經元網絡(b)Fig.1 CRNN network for single-step reaction (a) and multi-step reactions (b)

公式(1)中的反應表示為一個神經元，如圖1(a)所示，公式表示為y=σ(wx+b)，其中x為神經元的輸入，表示體系中各組分的質量濃度和溫度；y為輸出，表示體系中各組分的反應速率；w為權重，代指阿倫尼烏斯公式中的活化能和反應方程式中的化學計量系數；b為偏差，對應阿倫尼烏斯公式中的指前因子A；σ為非線性激活函數，可以避免過擬合現象。總的來說，Al-PTFE熱解過程涉及多個步驟，可以將單個神經元疊加，形成一個包含一層隱含層的神經網絡，如圖1(b)所示。神經網絡的隱藏層節點數等于基元反應的個數。神經網絡模型的損失函數定義為熱分解實驗的TG質量分數與模型預測的質量分數之間的平均絕對誤差：

(5)

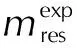
在Al-PTFE動力學建模的CRNN模型中加入了以下約束條件：(1) Al-PTFE只存在于反應物中；(2) 質量化學計量守恒；(3) 活化能Ea和lnA分別在0～300kJ/mol和-20～50范圍中取值。

1.2 訓練和驗證數據的選取

熱重實驗是測試物質熱分解特性的經典方法，可精確測量物質在特定升溫速率下，熱解過程中質量損失隨溫升的變化情況[36-38]。盡管多年來，眾多學者對Al-PTFE復合體系的熱解進行了研究，但由于各自實驗條件(升溫速率、氣體流速、樣品質量)和樣品特性(粒度大小、配比)等因素的不同，導致實驗結果有所差異[4,7,19,39,40]。本實驗以納米級鋁顆粒作為主要研究對象，選用毛亮[1]通過熱重分析測試的PTFE基納米Al活性材料的實驗數據，具體實驗參數如表1所示，Al/PTFE質量比為74∶26，通過濕混工藝制備，納米Al顆粒粒徑為50nm級。在訓練神經網絡時，為了避免過擬合，選取升溫速率分別為10、15、30℃/min的3組實驗作為訓練集，每組實驗包含不同時刻的數據點，共有2089個熱重數據點，選取升溫速率為20℃/min的實驗作為驗證集，在訓練神經網絡時每個時刻的數據都會單獨參與模型的訓練，為了進一步測試神經網絡動力學模型的泛化能力，又選取了一組升溫速率為5℃/min的熱重數據為驗證集，包含971個熱重數據點[41]。

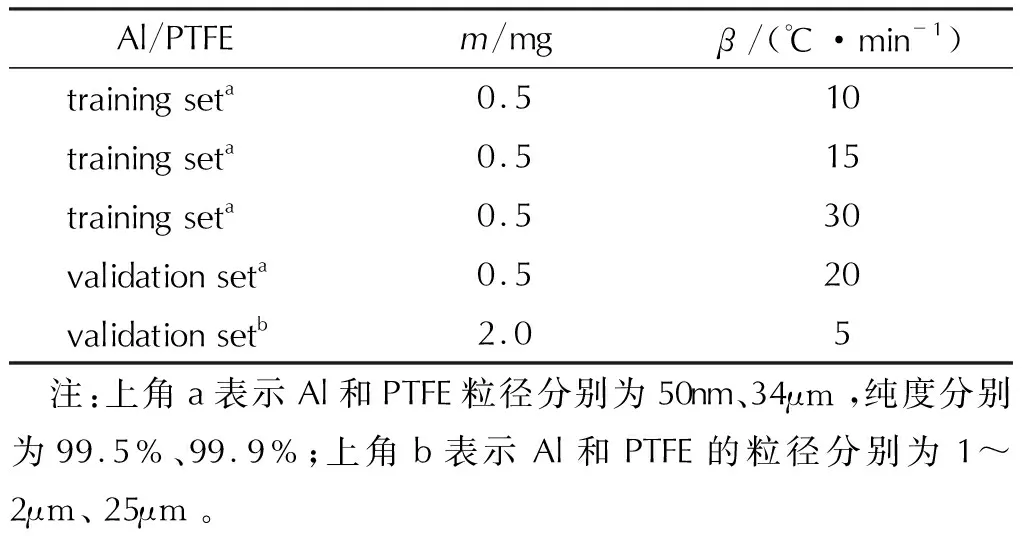
表1 Al-PTFE樣品和熱解實驗相關參數[1,41]Table 1 The parameters of Al-PTFE sample in the thermal decomposition experiments [1,41]

2 結果與討論

2.1 動力學模型分析

通過分別設置不同的物質數量和反應數量，利用CRNN框架推演納米Al-PTFE復合體系的動力學模型。圖2為包含5個反應(Number of reactions，nr)和5個物質(Number of species，ns)的動力學模型在訓練集和驗證集的計算誤差隨神經網絡迭代次數的演化。圖中實線代表損失函數的滑動平均值，取每個時刻前100步計算平均值。

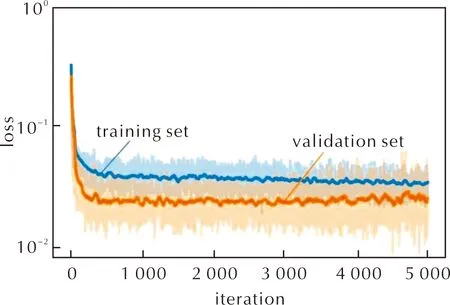
圖2 神經網絡模型在訓練集和驗證集的計算誤差隨迭代次數的演化(ns=5, nr=5)Fig.2 The errors of the CRNN model in the training set and validation set (ns=5, nr=5)

從圖2可以看出，訓練數據集在前300個迭代周期快速下降，誤差小于0.1。為了確保訓練精度，模型進行5000次迭代訓練。如1.2節所述，每個周期對3組訓練集數據進行模型訓練，并使用1組實驗數據進行驗證以避免過擬合。經過5000次迭代后，得到的模型對熱重實驗的預測誤差均小于0.1。

圖3為驗證數據集(升溫速率為20℃/min)在5000次迭代后的誤差與生成物質和反應數量的關系，圖中顏色的深淺表示損失函數值的大小，紅顏色表示誤差較小(單位為質量分數)。由圖3可知，反應數目和物質數量越大，損失函數值也就越小，總體平均損失值為0.085。這意味著更為詳細的動力學可以更好地闡釋熱重實驗數據。當組分數目小于4時，CRNN推演出的模型與熱重實驗在殘留物質量分數上的誤差較大(均大于0.1)。當物質組分數目大于等于4時，模型的誤差快速降低(大部分小于0.02)。但也有少數特殊例子，例如當反應路徑數目和物質數量分別為10和8時，誤差為0.07，比其他損失值(0.01～0.04)略大。在下面工作中，主要選取3組動力學模型作為討論對象，模型中包含的生成物質數和反應數相等，分別為3、4和5, 這3個模型名稱被簡化為3-3、4-4和5-5。

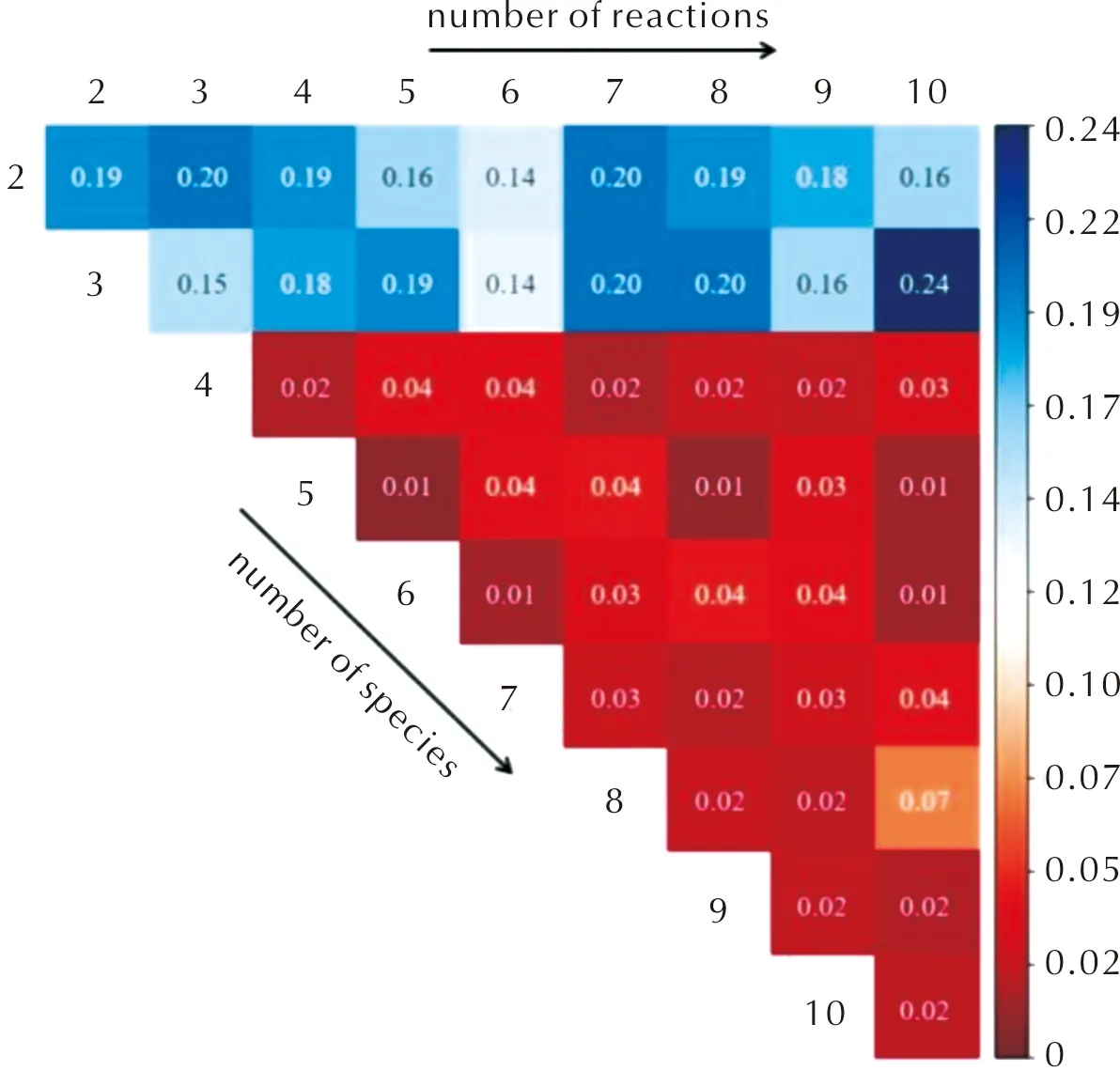
圖3 驗證數據集的損失函數與生成物質和反應過程的依賴關系Fig.3 The values in the loss functions of validation sets for all CRNN models

接下來利用3-3、4-4和5-5模型預測4種不同升溫速率條件下的Al-PTFE熱重數據。3種模型預測的熱重分解結果與實驗數據分別如圖4所示，其中圖4(a)～(c)分別是3-3、4-4和5-5的模型預測結果。從圖4(a)中可以看出，預測值與實驗值發生十分明顯的偏離，其誤差較大為0.15，說明生成物質和反應路徑數量設置較小時，對CRNN學習模型測試結果影響較大，無法重現實驗結果。圖4(b)中的預測值與熱重曲線的誤差為0.02，但在升溫速率為30℃/min條件下，預測值與實驗曲線有較小的偏離。圖4(c)中的預測值與熱重實驗數據的吻合度較高，誤差僅為0.01，可知在ns=5和nr=5條件下，采用CRNN框架對Al-PTFE復合體系訓練結果的準確度較高，將對此條件下的反應機理進行重點分析。

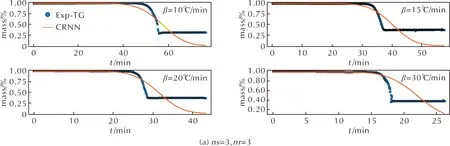
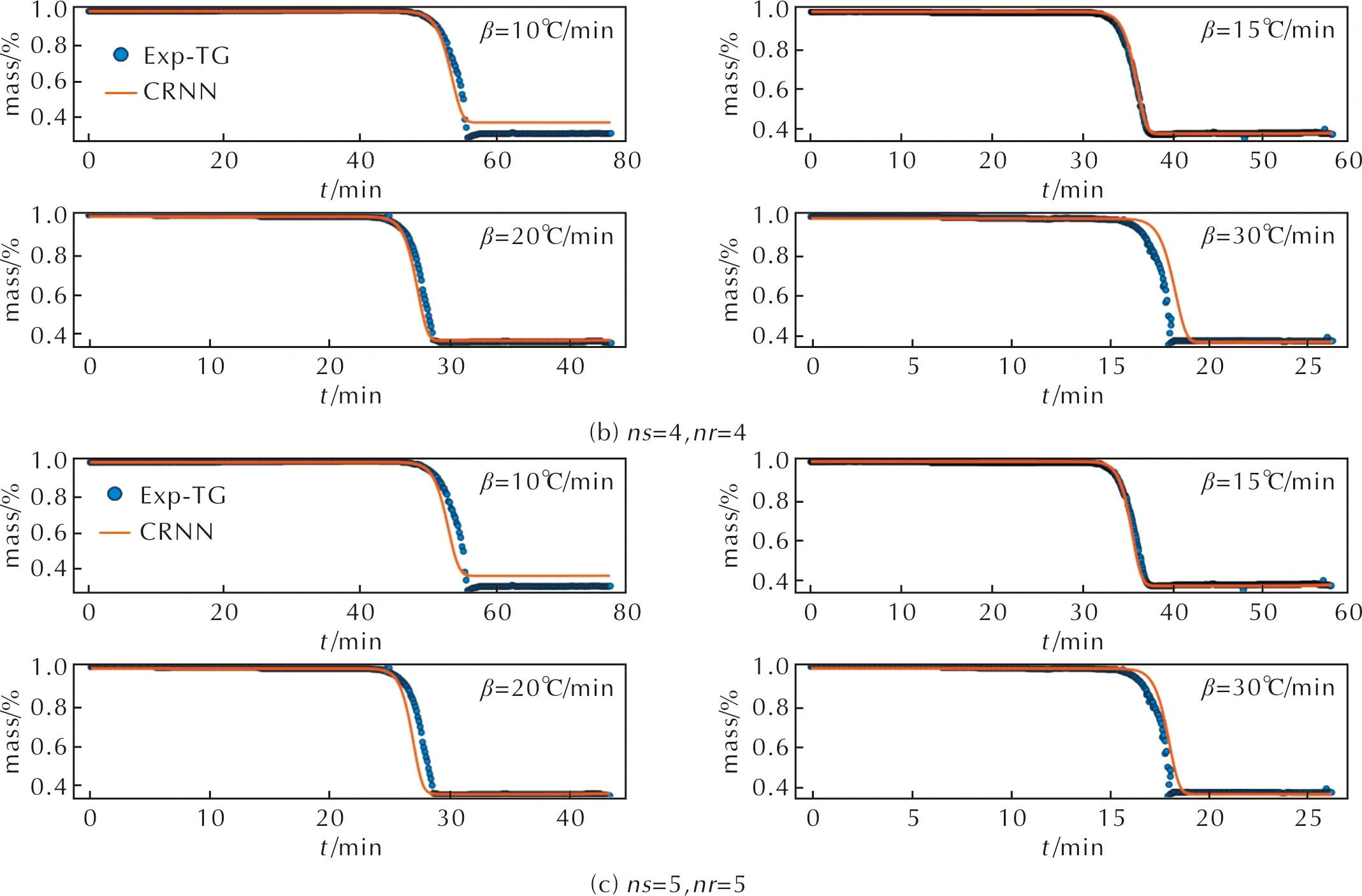
圖4 通過CRNN學習模型測試結果(實線)與TG實驗結果(圓點)的對比Fig.4 The predicted TG curves by the CRNN models (solid line) and experimental results (dot)

圖5包含CRNN框架推演得到的3個動力學模型 (3-3、4-4和5-5模型) 對于納米Al-PTFE復合體系熱分解反應過程中物質質量演化，相對應的反應模型如表2所示。在圖5(a)(3-3模型)中，Al-PTFE復合體系熱解起始時間比實驗要普遍早5～10min，同時熱解速率明顯要慢于實驗結果。由于路徑R3的系數為零，在本研究中忽略，實際整個反應模型只包含一個熱解總包反應和一個S2轉化為S3的反應。在整個模型中，S2作為主要熱解產物，質量快速增長，但是在反應后期速率減慢，有部分S2轉化為S3。S3作為熱解的副產物，質量占比遠小于S3。值得注意的是3-3模型中沒有包含任意反應中間體。4-4模型相較于3-3模型，增加了一個新的反應產物S4，其中反應路徑R2、R3和R4均是描述物質S3生成S2和S3的反應，反應路徑 R3的反應速率相對較快，從圖5分析可知，經過R2、R3和R4的反應，物質S3的質量逐漸為0，可知物質S3為反應中間物質。從圖4中已知4-4模型相比3-3模型可以準確描述熱重實驗曲線，這可能與新引入的S4有直接關系。

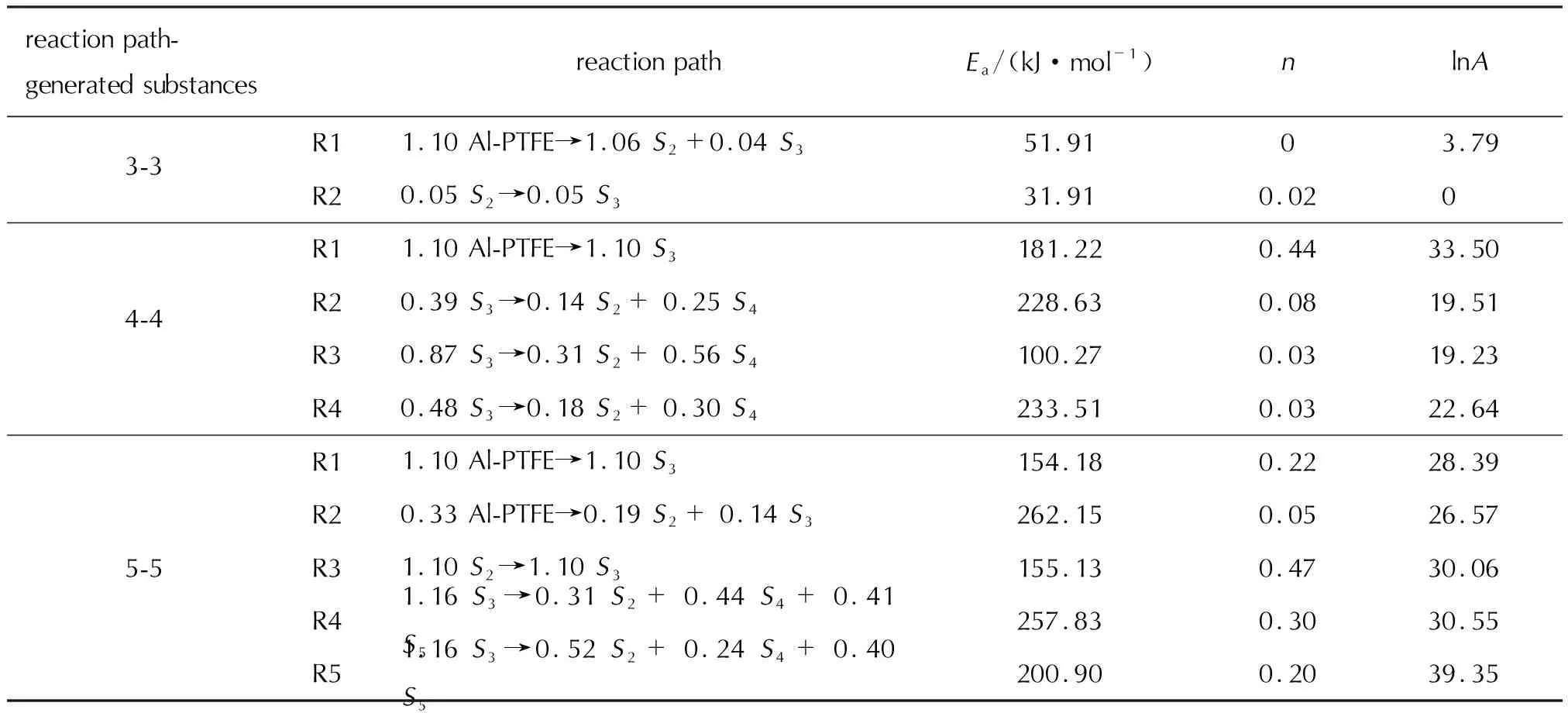
表2 CRNN框架下訓練得到的化學反應模型Table 2 The reaction mechanisms learned from the CRNN model

在圖5(c) (5-5模型)中，Al-PTFE體系的起始熱解反應為R1，有少部分反應物質Al-PTFE發生了另外一個反應R2，反應R1比R2的反應速率相對較快，反應路徑R2中生成S2和S3。R4和R5的反應路徑均是描述S3轉化為S2、S4和S5的反應，其中R5的反應速率比R4高約4個數量級，因此R4反應實際可以被簡化。根據圖5的物質分布曲線可知，經過反應路徑R4和R5，物質S3質量減少，待反應結束，其質量為0，可知S3為反應中間物質。以反應體系的初始質量為參考，S5的質量濃度較大，為65%，S2和S4保持在10%～25%之間，S2、S3和S5為主要產物。

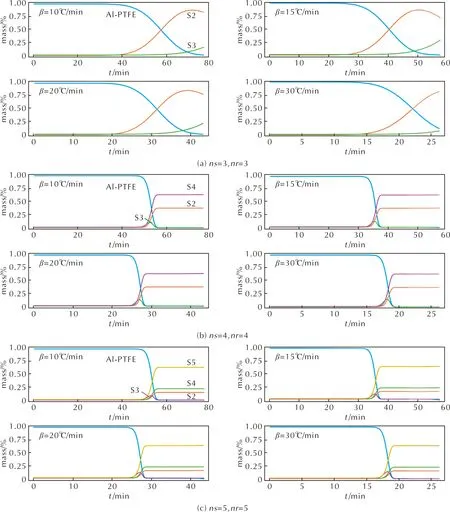
圖5 通過CRNN學習模型預測納米Al和PTFE熱分解的物質演化過程Fig.5 The species evolutions of nano Al and PTFE composite during the thermal decomposition predicted by the reaction mechanisms derived from CRNN model

為了說明CRNN模型的泛化能力，本節中選取了另外一組Al-PTFE熱重數據[41]為驗證集。由于納米級的Al-PTFE熱重實驗相關數據較少，因此本實驗選取了微米級的Al-PTFE熱重數據。此樣品質量為2mg，和訓練集的熱重實驗參數有明顯差別，具體參數如表1所示。CRNN模型的計算結果如圖6所示。由圖6可知，Al-PTFE的模型驗證結果和熱重曲線的吻合度與前文 (圖4)中計算基本一致，3-3組的預測值和實驗曲線的偏離較大，4-4和5-5的預測值和熱重實驗值吻合度相對較高。與圖5(c)中的5-5模型相比，圖6(c)中的物質S2質量分數相對較少，為12%左右，而圖5(c)中的S2質量分數為18%左右，這可能是因為熱重實驗樣品參數的不同所導致。從以上分析可知，CRNN模型提出的反應機理具有一定的泛化能力，可以預測到其他Al-PTFE熱重數據。

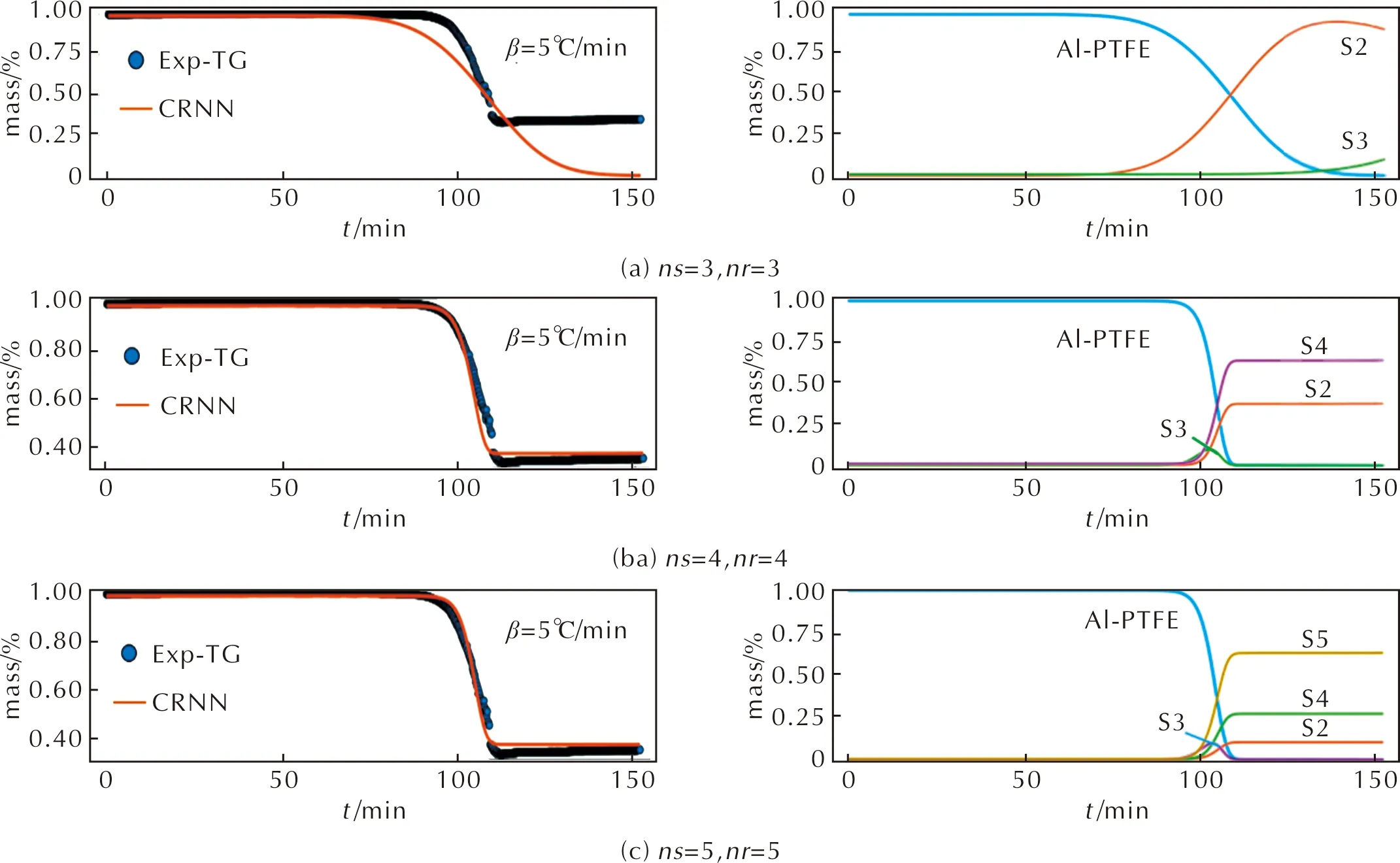
圖6 通過CRNN模型對另外一組Al和PTFE熱重數據的計算結果 Fig.6 The calculation results of another set of Al and PTFE thermal decomposition data through CRNN model

2.2 Al-PTFE復合體系動力學反應機理

在納米鋁顆粒和PTFE反應體系中，納米鋁顆粒為還原劑，PTFE則起到氧化劑的作用，總包化學反應可分為兩種情況，如圖7所示。

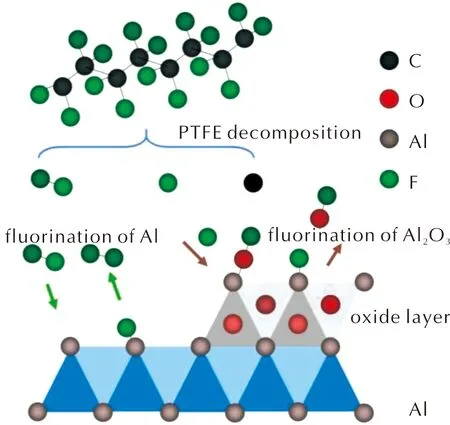
圖7 Al顆粒與PTFE 反應機理示意圖Fig.7 Reaction mechanism of Al with PTFE

第一種為零氧平衡下的反應，為反應(1)[42]，此反應無其他氧化劑的參與。但從以往研究中可知，納米鋁顆粒表面總有一層致密的Al2O3氧化層[43-45]，因此Al2O3可能參與其中的反應，如反應(2)所示，生成的碳氧化合物 (COn代表CO、CO2或二者的混合)。反應(1)和(2)均為鋁顆粒和PTFE在熱解反應過程中的總包反應，主要生成物質為AlF3、Al4C3、C和碳氧化合物。本研究分析的對象納米Al-PTFE是通過濕混工藝制備的聚四氟乙烯基鋁活性材料，納米鋁顆粒吸附在PTFE表面，質量配比為74∶26，Al與PTFE的反應剛好符合零氧平衡，但鋁顆粒的表面有Al2O3氧化層。在Al-PTFE復合體系熱解過程中涉及氟聚物分解，以及碳化氟小分子與Al和Al2O3的反應[45]，反應機理較為復雜。因此，并不能簡單地按照反應(1)和(2)對納米Al-PTFE復合體系的反應機理進行分析。此處結合從神經網絡學習到的反應動力學網絡對反應機理進行大致的推測，如圖7所示。

4Al+3(-C2F4-)→4AlF3+6C

(1)

6Al+Al2O3+3(-C2F4-)→4AlF3+Al4C3+2C+COn

(2)

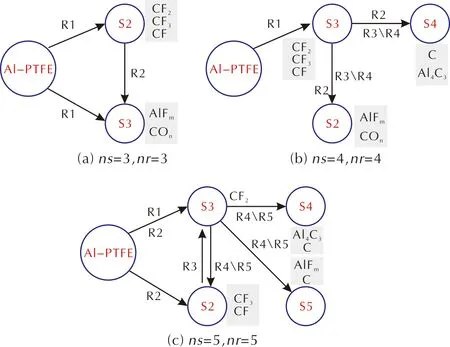
圖8 CRNN模型推演出反應網絡Fig.8 Reaction network derived from CRNN models

基于熱重實驗曲線，本研究通過CRNN模型提出了多步反應機理。圖8為不同路徑和生成物質的反應網絡，由于缺乏分解產物的實驗數據，將依據神經網絡學習得到的反應機理來推測Sn代表的物質。當反應路徑和生成物數量均為3時，由于網絡中組分數目不足，沒有固體產物的生成(Al4C3和C)，導致模型精度很差。對于4-4和5-5模型的反應網絡結構足夠復雜，可以描述主要的分解產物演化。從上述2.1節分析可知，5-5模型的反應機理比其他兩種反應機理更貼近Al-PTFE復合體系的反應過程，下面將對該機理進行進一步分析。在WANG Jun[46]對納米Al-PTFE復合體系研究中發現，PTFE在熱解初始階段可能存在兩種反應，分別生成CF2以及CF3和CF，其中CF2為主要產物。在納米Al-PTFE聚合物中，納米Al顆粒吸附在微米級PTFE的表面，所以先由與PTFE接觸的Al2O3薄膜與PTFE的分解產物(CF2、CF3、CF)發生反應，隨著反應的進行，氧化膜Al2O3發生破損，Al開始加入反應。參照5-5模型的形式，提出如下反應機理：

(-C2F4-)→CF2

(3)

(-C2F4-)→CF3+CF+CF2

(4)

CF3+CF→CF2

(5)

Al+Al2O3+CF2→a(CF3+CF)+

b(Al4C3+COn) +c(AlFm+C)

(6)

Al+Al2O3+CF2→a′(CF3+CF)+

b′(Al4C3+COn)+c′ (AlFm+C)

(7)

其中反應 (3)和(4)代表氟聚物的熱分解，生成CF2、CF3和CF。從表2中的動力學參數可知R1反應速率遠大于R2，這與WANG Jun[46]發現CF2物質為主要產物的動力學行為相一致。此外，反應(5)代表碳化氟小分子間的轉化。上述反應(3)、(4)、(5)主要涉及氟聚物和碳化氟小分子的反應，與5-5模型中的R1、R2、R3相對應。反應(6)和(7)則分別表示氟聚物的分解產物與納米鋁粉的氧化層、鋁核的反應路徑，與5-5模型中的R4、R5相對應。反應(6)和(7)中的AlFm和COn表示氣相的氟化鋁(如AlF3)和碳氧化物(CO和CO2)。反應(6)相較于反應(7)更傾向于生成Al4C3和COn，而反應(7)更傾向于生成更多的碳化氟小分子。值得注意的是R5反應速率在熱解溫度區間中均遠大于R4反應，這一動力學現象與R4反應主要發生在鋁粉顆粒氧化層破碎前有直接關系。在5-5模型中，反應路徑R5中的活化能為200.9kJ/mol，與文獻[1]中總包反應的活化能208.5kJ/mol十分接近，此反應路徑為體系的主要反應。S3(CF2)為反應的中間產物，這可能由于CF2的反應活性較強所導致。結合已有文獻，推測Al-PTFE復合體系反應生成的固體產物主要為Al4C3和C，氣態產物為AlFm和碳氧化合物。

以上是基于CRNN模型進行的推斷，但在Al-PTFE復合體系實際分解反應過程中受多方面因素的影響，如Al顆粒表面Al2O3的厚度，樣品質量比、反應氣氛等因素。為提高模型學習的結果，在未來工作中，可在不同實驗條件下進行多組測試，分析這些因素對實驗結果的影響規律。還可借助于其他測試手段，如采用質譜分析、X射線衍射和紅外光譜對樣品分解產生的物質進行實時測量，為物質生成、反應路徑的準確預測提供約束條件，有助于開發出符合化學和物理規律的含能材料熱分解模型。

3 結 論

(1) 以納米Al-PTFE復合體系的熱重實驗數據為基礎，提出了一種基于神經網絡建立化學反應機理的方法，對納米Al-PTFE反應機理進行動力學建模，預測納米Al-PTFE可能存在的反應路徑、生成物質和相應的動力學參數。此模型還可以對物質的殘余質量分布進行準確預測，有效識別未知中間體的質量變化。

(2) 結合CRNN模型學習的基元反應網絡和Al-PTFE的總包反應，預測了納米Al-PTFE可能存在5步基本反應，首先是C2F4的分解和氣化反應，之后是納米鋁顆粒最外層的Al2O3薄膜與C2F4的分解產物發生反應，氧化膜破損，顆粒內部的Al釋放發生主要反應，活化能為200.9kJ/mol，與總包反應的活化能非常接近，中間物質可能包括氣化的CF、CF2、CF3等物質，生成的固體產物為Al4C3和C，氣態產物為碳氧化合物，可能包括CO2或者CO。

(3) 與傳統的反應動力學建模方法相比，CRNN模型不需要實驗樣品的具體性質，反應路徑(化學計量系數)和動力學速率常數都被視為可優化的參數，不需要對反應路徑的先驗知識。該方法還可以擴展到其他含能材料，為其動力學模型開發提供一定借鑒及參考。