廣告牌支架梁貫通式節點極限承載力數值分析

時維周學軍周雅馨

(1.山東建筑大學 土木工程學院，山東 濟南250101；2.同圓設計集團，山東 濟南250101)

0 引言

廣告牌作為一種直觀的廣告載體，已經成為行業傳播信息的重要方式之一，其支架的安全性受到了工程界的廣泛重視，國家和地方也發布了相應的廣告牌設計標準和設計圖集，其可以規范和指導廣告牌的設計和制作[1-3]。常見的廣告牌結構形式多采用單柱或多柱懸臂結構，其頭大腳小、自重輕，主要承受自重、風荷載和地震作用。李海旺等[4]通過ANSYS有限元分析軟件對廣告牌整體結構進行受力分析，研究其整體受力狀態；戴卓見[5]針對廣告牌受風荷載的結構特征，研究了廣告牌的設計理念；汪大海等[6]以單立柱三面廣告牌為試驗對象，為完善大型廣告牌結構的抗風設計提供了相應計算理論方法；李志豪[7]研究了廣告牌整體結構的風荷載及風振響應特性。而目前對廣告牌節點承載性能的研究較少，特別是獨立柱式廣告牌，連接節點一旦失效便會導致廣告牌傾斜或倒塌，存在極大安全隱患[8]。文章采用有限元軟件ABAQUS建立廣告牌支架節點模型，研究了梁貫通式、無內隔板柱貫通式、帶內隔板柱貫通式3種形式的梁柱節點的極限承載力及其破壞模式，以期為實際工程中該節點的使用可靠性和適用范圍提供參考依據。

1 廣告牌支架梁貫通式節點有限元模型建立

廣告牌支架一般采用鋼管結構，如圖1所示，梁柱構件均為圓管鋼。梁柱連接形式主要為梁貫通式節點、無內隔板柱貫通式節點和帶內隔板柱貫通式節點[9-11]，工程中多采用梁貫通式梁柱連接節點，如圖2所示。但在實際工程中發現，梁、柱等直徑時仍采用梁貫通式節點，類似于柱被梁截斷，存在較大的安全隱患，因此為探討梁貫通式梁柱節點的受力性能和適用范圍，文章利用有限元軟件建立了3種類型節點的計算模型，研究不同工況下節點的極限承載力及其破壞模式。

1.1 單元類型和參數設計

利用ABAQUS有限元軟件建立梁柱節點模型[12]，單元類型選用四邊形四結點曲面殼單元減縮積分(S4R)，采用Q235鋼材，其彈性模量E＝2.06×105MPa、泊松比μ＝0.3。鋼材本構關系選用簡化的三折線理想應力—應變曲線模型，如圖3所示。實際工程中梁柱節點一般采用全熔透焊縫，焊縫強度與母材等強，工程應用和試驗研究表明，將梁柱焊接節點簡化成剛接節點與實際情況區別不大。因此，為了方便分析，在建模時將梁柱節點直接綁定作為分析的剛接節點。

圖1 廣告牌支架示意圖

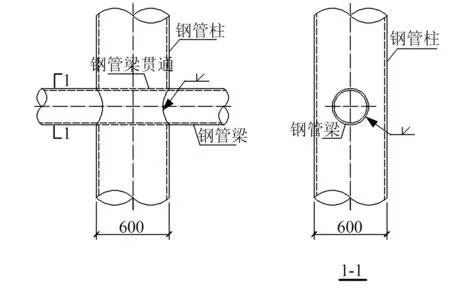
圖2 梁貫通式節點設計圖/mm

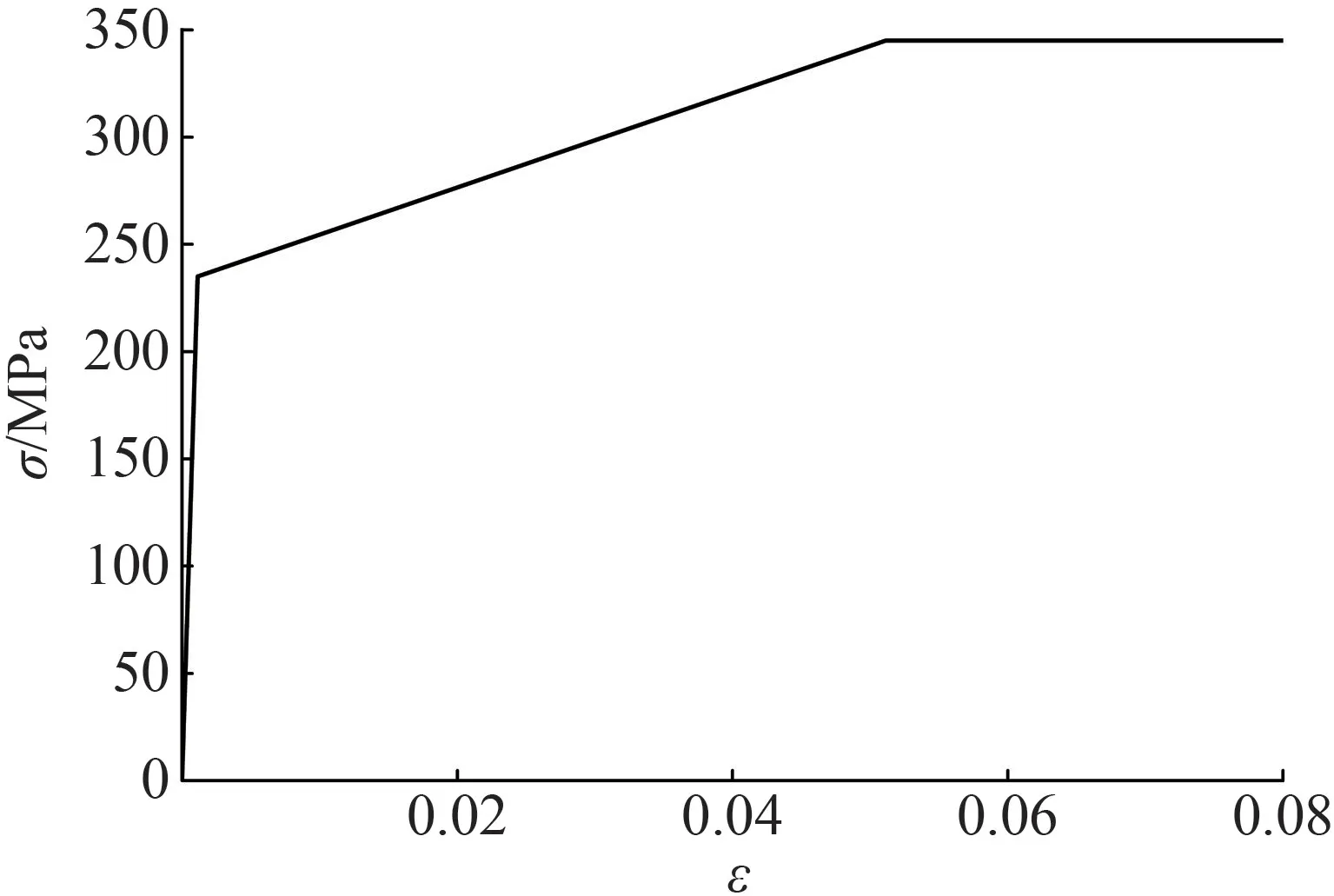
圖3 Q235鋼材應力—應變曲線圖

1.2 邊界條件和載荷條件

根據構件使用時的實際受力情況，節點模型取廣告牌承重框架梁柱反彎點之間的一個脫離體進行分析[13-15]，為一個“十字形”試件，將柱上、下端及兩側梁遠端各耦合為一個點，通過耦合點設置邊界條件及載荷條件，柱底約束x、y、z3個方向的位移，柱頂約束x、y兩個方向位移。為模擬柱在實際使用中所受的軸向壓力作用，在柱頂耦合點上施加一個軸壓比為0.2的豎向軸壓力；為模擬節點在實際工程中所受的彎矩作用，通過梁端的耦合點施加豎向力，梁兩端加載方向相反。邊界條件及載荷條件設置如圖4所示。

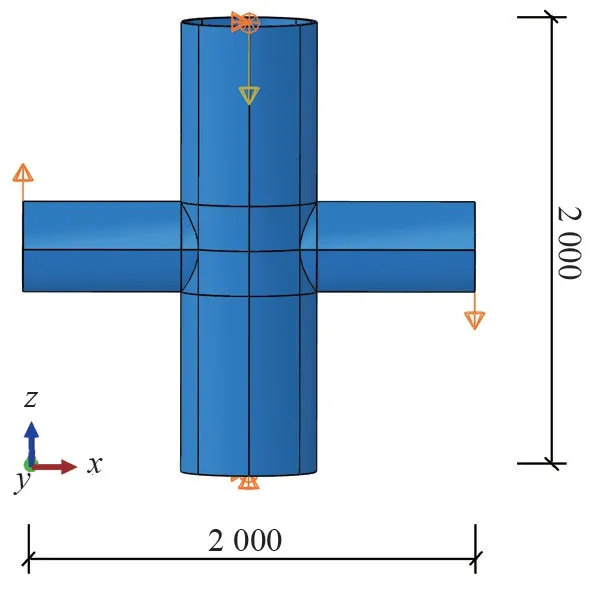
圖4 節點有限元模型圖/mm

1.3 節點模型尺寸

模型節點尺寸為2 000 mm×2 000 mm，鋼管柱壁厚為20 mm保持不變，為了便于對照分析，以梁柱直徑比和鋼管梁壁厚作為控制變量，分別建立梁貫通式、無內隔板柱貫通式、帶內隔板柱貫通式3種節點模型，模型設計參數見表1～3。表中圓管梁、柱尺寸以“直徑×壁厚”表示，如“600×20”表示圓管直徑為600 mm、壁厚為20 mm。

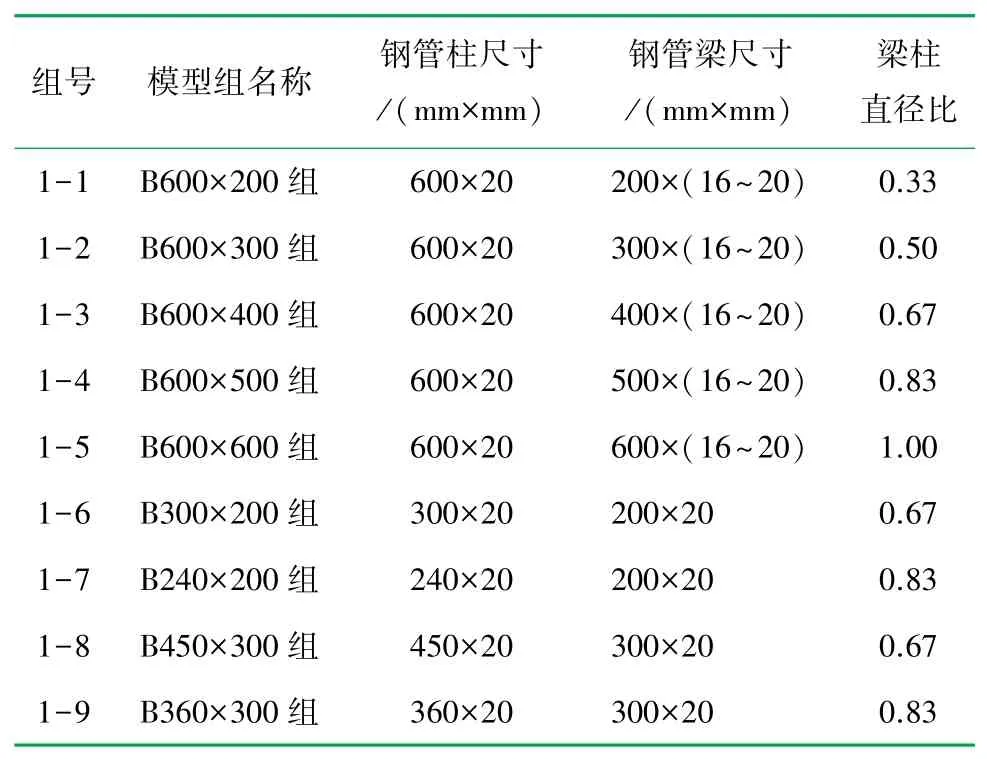
表1 梁貫通式節點模型設計參數表

表2 無內隔板柱貫通式節點模型設計參數表

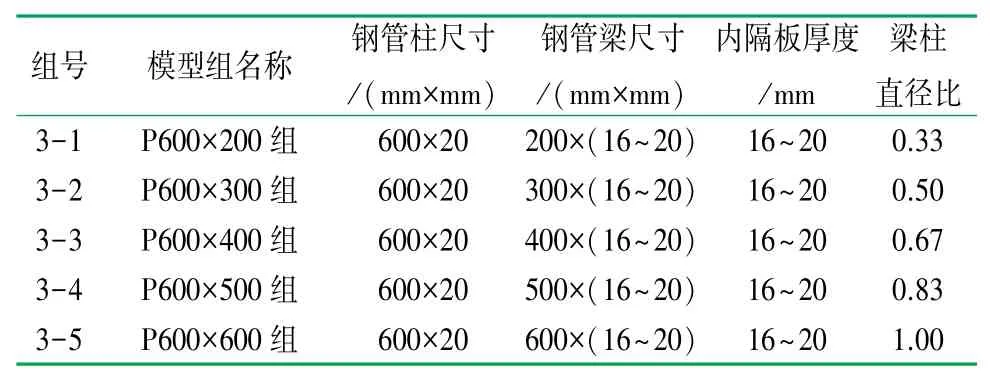
表3 帶內隔板柱貫通式節點模型設計參數表

1.4 有限元模型驗證

為衡量所建有限元模型的準確性，以某圓鋼管空間相貫節點試驗結果[16]為參照，根據文中的有限元模型建模方法建立了該空間相貫鋼管節點的有限元模型，如圖5所示，并分析了節點極限承載力。有限元分析的節點荷載—位移曲線和文獻[16]中試驗得到的荷載—位移曲線如圖6所示，二者吻合較好；同時有限元分析得到的節點極限承載力(1 734.7 kN)和試驗得到的節點極限承載力(1 670.2 kN)相比，誤差僅有3.86%，表明所建立的有限元模型及其分析方法的準確性和精確性。

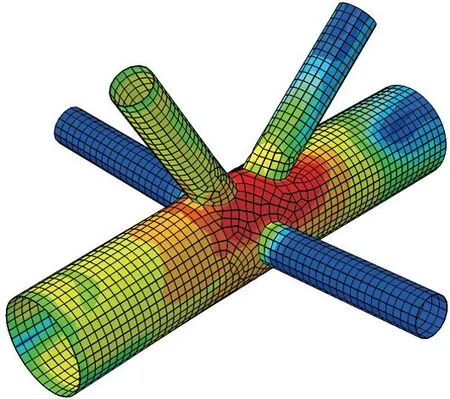
圖5 XK型節點有限元模型Mises應力云圖

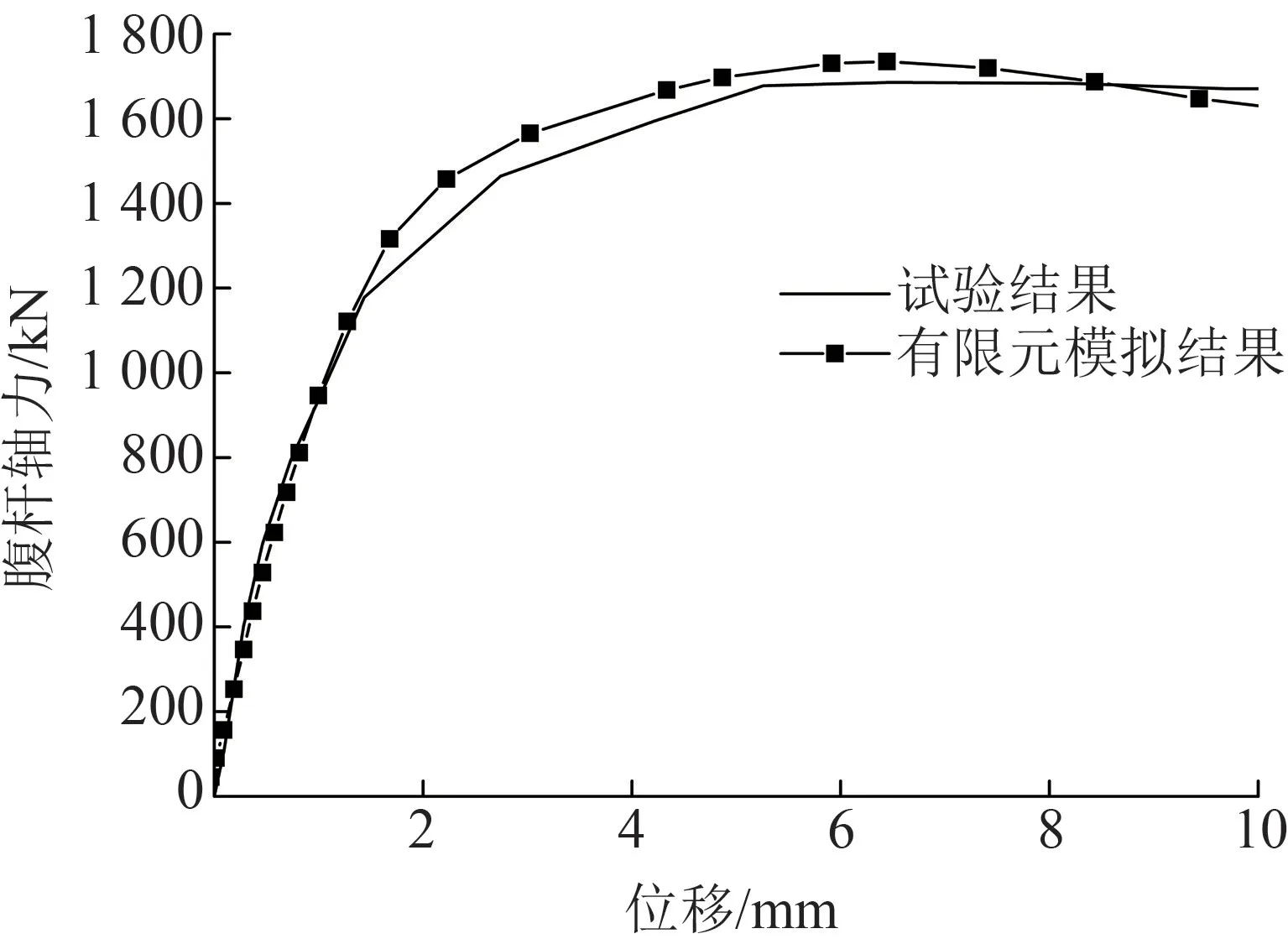
圖6 XK型節點有限元模擬與試驗模結果對比圖

2 模擬結果與分析

2.1 梁貫通式節點極限承載力分析

對梁貫通式節點模型進行極限承載力有限元分析，得到節點極限承載力值見表4。結果表明，圓管梁壁厚對節點極限承載力的影響會隨著圓管梁直徑的增大而增大，當圓管梁直徑為200 mm時，增加壁厚使節點極限承載力提高約為18.47%；當圓管梁直徑為600 mm時，增加壁厚使節點極限承載力提高約為28.69%，說明梁直徑越大，壁厚對節點極限承載力影響越大。

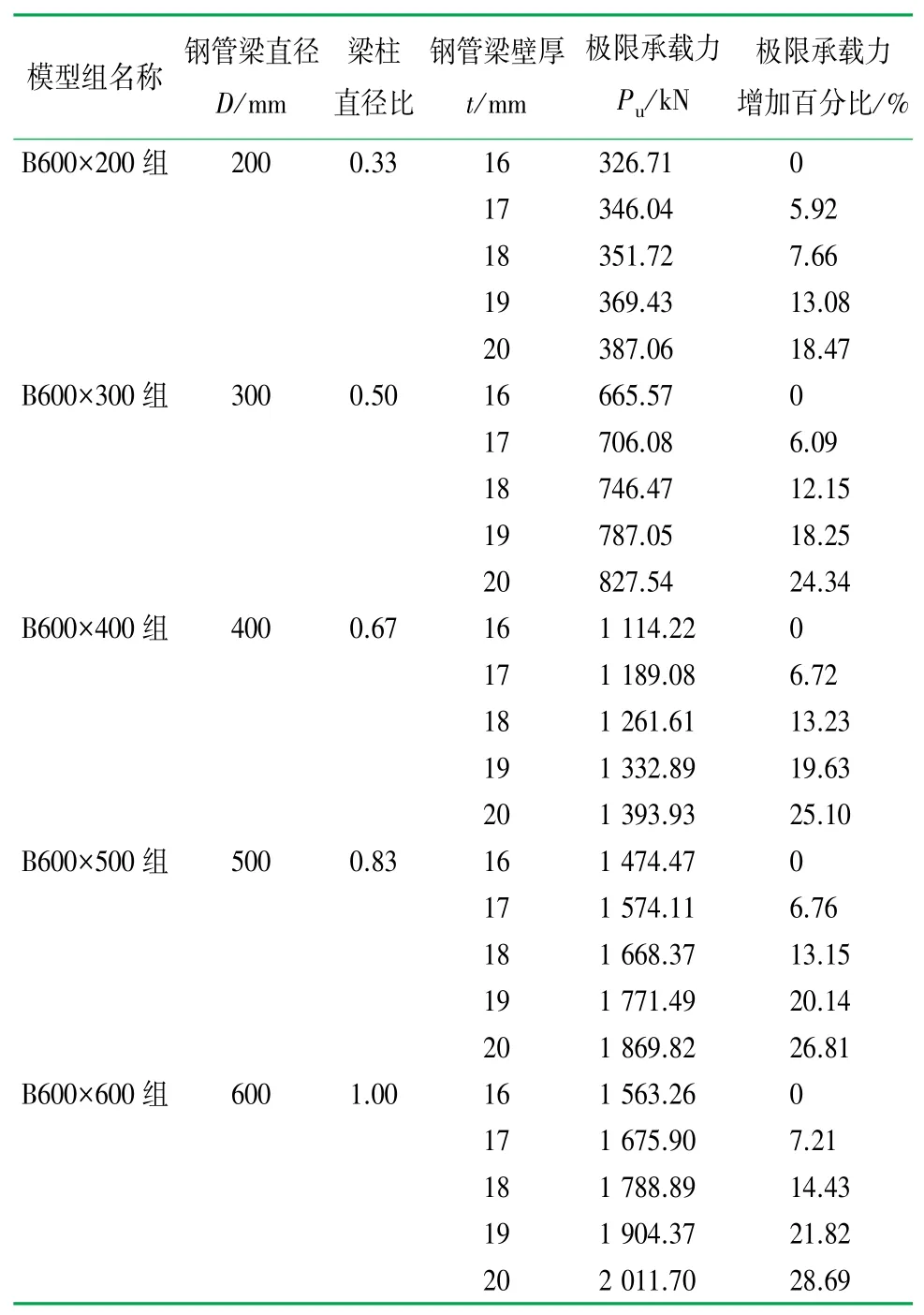
表4 梁貫通式節點極限承載力分析表

為更直觀、方便地分析計算結果，將有限元計算結果繪制成曲線，如圖7、8所示。由圖7中曲線的整體趨勢可知，當梁直徑在300～500 mm即梁柱直徑比為0.5～0.83范圍時，節點極限承載力提高最快；當梁直徑超過500 mm即梁柱直徑比超過0.83后節點極限承載力增長幅度變緩，但極限承載力仍是上升趨勢。由圖8可知，節點極限承載力與梁直徑、圓管梁壁厚呈正相關。增加圓管梁壁厚不如增加梁直徑提高節點承載力顯著。因此，對于圓管梁截面而言，改變梁截面直徑比改變圓管壁厚提高節點的極限承載力更為有效。

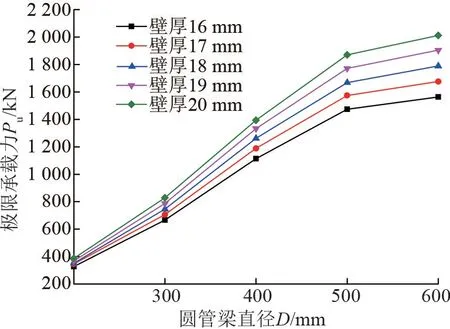
圖7 梁貫通式節點極限承載力—圓管梁直徑曲線圖

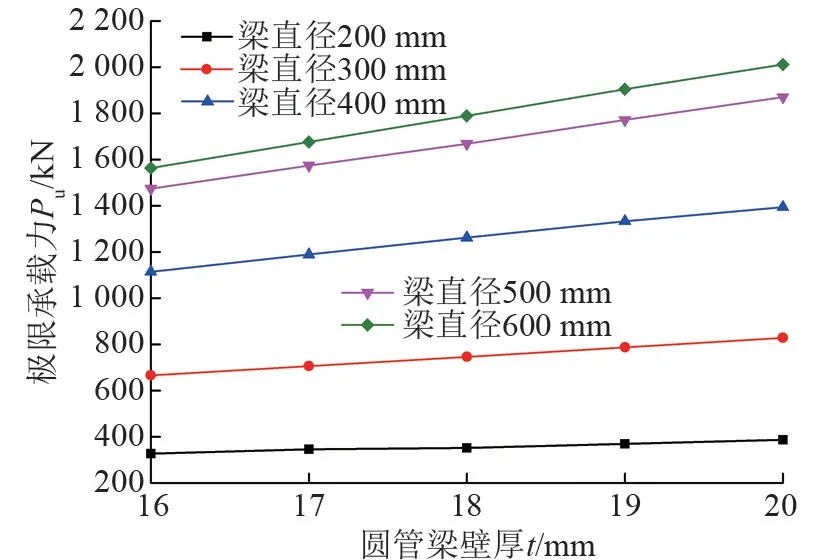
圖8 梁貫通式節點極限承載力—圓管梁壁厚曲線圖

分析梁貫通式節點前5組模型的馮·米塞斯Mises應力云圖發現，同一組內模型圓管壁厚的改變對節點極限承載力影響較小，節點破壞模式也相同，但梁直徑的改變對節點破壞模式有顯著影響。圓管梁壁厚為20 mm時，梁直徑由200 mm增加到600 mm時的Mises應力云圖如圖9所示。隨著梁直徑的增大，節點處的破壞模式也由梁端出現塑性鉸破壞轉變為節點域破壞。

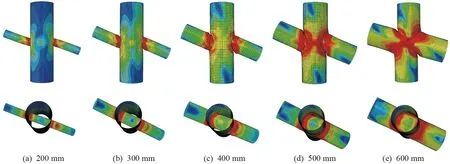
圖9 梁壁厚20 mm時不同直徑的梁貫通式節點Mises應力云圖

梁貫通式節點模型的有限元分析結果見表5。可以看出，當梁柱直徑比≤0.67時，節點的破壞模式表現為梁端出現塑性鉸破壞；當梁柱直徑比＞0.67時，節點的破壞模式表現為節點域破壞，不能滿足工程中“強節點弱構件”的要求。

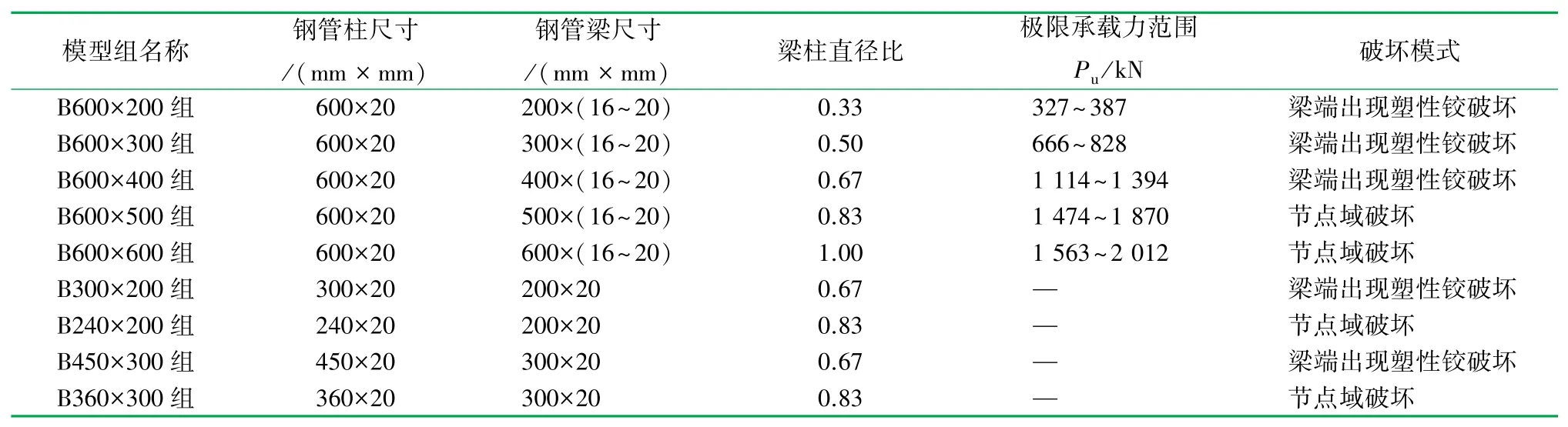
表5 梁貫通式節點模型有限元分析結果表

2.2 無內隔板柱貫通式節點極限承載力分析

無內隔板柱貫通式節點多用于民用建筑框架結構中，作為梁貫通式節點的對照組，目的是研究兩種節點形式的極限承載力和破壞模式的異同。節點的有限元模型設計參數見表2，模型各參數、尺寸不變，圓管梁截斷與圓管柱通過對接焊縫連接，柱子截面不削弱。

有限元分析發現，所有節點模型的破壞過程皆為靠近梁柱相交處的柱身先發生局部屈曲，隨著荷載增大，柱身塑性區域進一步擴大，最后擴展到梁端，整個過程柱子先于梁破壞。無內隔板柱貫通式節點破壞形態如圖10所示。

圖11為圓管梁壁厚為20mm時，不同梁直徑的無內隔板柱貫通式節點的Mises應力云圖。不論圓管梁尺寸如何變化，無內隔板柱貫通式節點的破壞模式都表現為柱端出現塑性鉸破壞。對于無內隔板柱貫通式節點，由于圓管柱中沒有內隔板加強，對圓管梁施加荷載時梁柱相交處因復雜應力狀態先發生局部屈曲，柱身出現塑性區。

圖10 無內隔板柱貫通式節點破壞形態圖

圖11 梁壁厚20 mm時不同直徑的無內隔板柱貫通式節點Mises應力云圖

2.3 帶內隔板柱貫通式節點極限承載力分析

為進一步研究通過內隔板加強的柱貫通式節點的極限承載力和破壞模式，在柱貫通式節點中添加內隔板進行加強并進行有限元分析。兩個內隔板的位置分別與圓管梁上下表面處相對應[17]，且內隔板厚度與圓管梁厚度相同，如圖12所示。

將帶內隔板柱貫通式節點與梁貫通式節點的受力狀態進行對比，發現兩者的受力性能和破壞模式類似，同一組內模型圓管梁壁厚的改變對節點處受力性能的影響不大，節點破壞模式也相同，但梁直徑的變化對節點的極限承載力有較大影響。圓管梁壁厚為20 mm時，不同梁直徑的帶內隔板柱貫通式節點的Mises應力云圖如圖13所示。當梁柱直徑≤0.5時，節點的破壞模式表現為梁端出現塑性鉸破壞；當圓管梁直徑＞0.5時，節點的破壞模式表現為節點域破壞。

梁貫通式節點與帶內隔板柱貫通式節點有限元計算結果對比見表6。兩種節點形式的極限承載力接近。

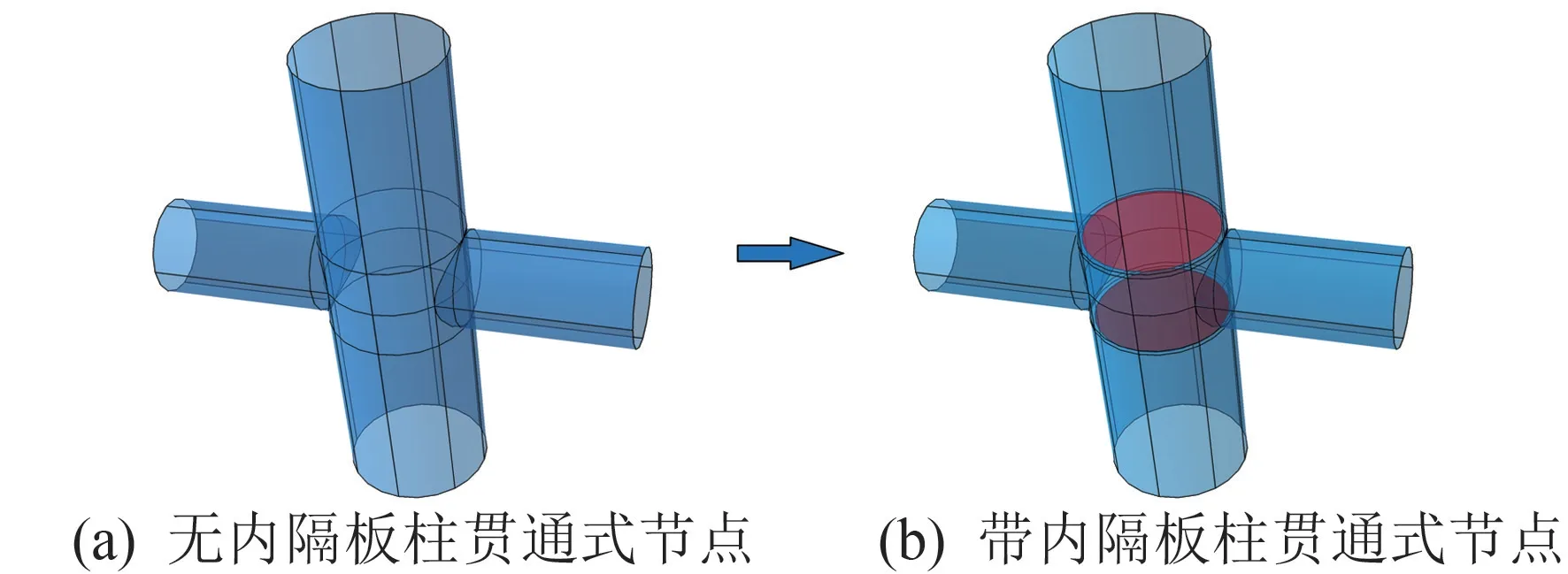
圖12 帶內隔板柱貫通式節點示意圖

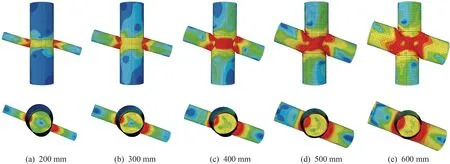
圖13 梁壁厚20 mm時不同直徑的帶內隔板柱貫通式節點Mises應力云圖

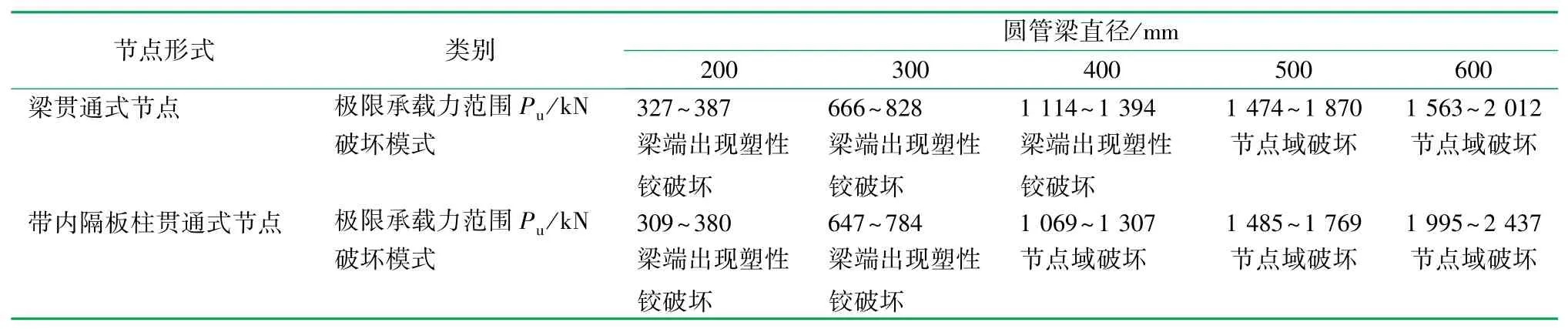
表6 梁貫通式節點與帶內隔板柱貫通式節點有限元分析結果對比表

3 結論

利用有限元軟件，對梁貫通式、無內隔板柱貫通式、帶內隔板柱貫通式3種節點形式的極限承載力及其破壞模式進行了對比分析，得到的主要結論如下:

(1)梁貫通式節點的受力性能優于無內板的柱貫通式節點，增加內隔板能夠改善柱貫通式節點的受力性能，帶內隔板的柱貫通式節點受力性能與梁貫通式節點類似。

(2)圓管梁壁厚和梁柱直徑比是影響節點極限承載力的主要因素；相較于圓管梁壁厚因素，梁柱直徑比的變化對節點極限承載力的影響更為顯著。

(3)梁貫通式節點的梁柱直徑比≤0.67時，其破壞模式為梁端塑性鉸破壞；當梁柱直徑比＞0.67時，其破壞模式為節點域破壞。而對于帶內隔板的柱貫通式節點，梁柱的直徑比界限值則為0.5。