具有Logistic輸入和密度制約的一類階段結(jié)構(gòu)傳染病模型

劉亭亭，喬志琴

（中北大學(xué) 理學(xué)院，太原 030051）

1 研究背景

研究傳染病的發(fā)病機理、傳染規(guī)律和防治策略是醫(yī)學(xué)研究的重要內(nèi)容［1］。然而在現(xiàn)實世界中，諸如麻疹、水痘、猩紅熱等傳染病多見于幼年時期，白喉、淋病、性病等傳染病則多見于成年階段。因此，研究階段結(jié)構(gòu)的傳染病具有重大現(xiàn)實意義。對于階段結(jié)構(gòu)的傳染病，許多專家和學(xué)者已經(jīng)進行了大量的研究［2－16］。文獻［2－3］研究了單種群結(jié)構(gòu)的模型，文獻［4－8］主要研究了幾類階段結(jié)構(gòu)的幼年患病傳染病模型。文獻［9－16］主要研究了幾類階段結(jié)構(gòu)的成年患病傳染病模型。

隨著研究的深入，研究人員發(fā)現(xiàn)溫度、食物、空間等都會引起種群數(shù)量的變化，由此提出了環(huán)境容納量的概念，并引入了Logistic輸入這一概念。幼年個體向成年個體的發(fā)展過程中，需要獲取一系列的資源來保持自身的增長。當(dāng)個體所需資源非常相似時，競爭就會相當(dāng)激烈，出現(xiàn)種內(nèi)競爭。由于分析的復(fù)雜性，很多模型在研究過程中都沒有考慮密度制約［16］。

本文在前人研究的基礎(chǔ)上，考慮并分析了一類具有Logistic輸入和幼年受密度制約的階段結(jié)構(gòu)傳染病模型。假設(shè)種群中個體生長分為幼年和成年兩個階段，疾病僅在成年種群中傳播，幼年個體以Logistic形式輸入，并受密度制約，而成年個體不受密度制約。x＝x（t）、y＝y(tǒng)（t）和z＝z（t）分別表示t時刻幼年、成年易感者和成年染病者的數(shù)量，N（t）＝x＋y＋z表示t時刻種群的個體總數(shù)量。假設(shè)所有參數(shù)均為正，其中參數(shù)r表示內(nèi)稟增長率；K表示環(huán)境容納量；d1、d2表示幼年個體、成年易感個體自然死亡率；d3表示成年染病者的移除率，包含自然死亡、因病死亡等；m表示單個幼年個體的平均成熟率；η表示幼年個體的密度制約系數(shù)；β表示疾病的傳染率系數(shù)并建立以下傳染病模型：

本文中側(cè)重對初值（x（0），y（0），z（0））限定在集合D＝｛（x，y，z）∈R3＋｜x＞0，0＜y≤K，z＞0｝上系統(tǒng) （1）的解（x（t），y（t），z（t））的分析，其中t≥0。系統(tǒng) （1）對應(yīng)流程如圖1所示。

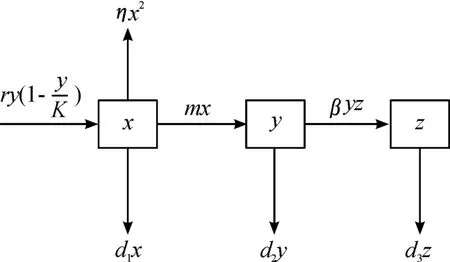
圖1 疾病傳播流程示意圖

引理1 初始條件在D上系統(tǒng) （1）的t≥0部分的解均為正的。

由以上結(jié)論可知，系統(tǒng) （1）的初值落在D中，其解軌線均為正解。證畢。

引理2 系統(tǒng)（1）的一切正解最終有界。

證明：將系統(tǒng) （1）的3個等式相加，并令d＝min｛d1，d2，d3｝，可以得到

根據(jù)比較定理［17］可以得到 limt→＋∞sup N≤rK／4d。所以對 ε＞0，-T＞0，當(dāng)t＞T時，x（t）＜rK／4d＋ε，y（t）＜rK／4d＋ε，z（t）＜rK／4d＋ε。因此，系統(tǒng)（1）一切正解最終有界。證畢。

2 平衡點的存在性分析

為了后續(xù)研究的方便，引入以下參數(shù)：

其中R0和Re0分別表示階段結(jié)構(gòu)種群的基本再生數(shù)和傳染病的基本再生數(shù)，顯然有Re0＜R0。

定理1

證明：系統(tǒng)（1）的平衡點滿足以下方程組：

由第3式可得，z＝0或y＝d3／β。

當(dāng)z＝0時，代入方程組（2）的第2式知

并由式（2）的第1式可得

則可解得x＝0或

且y0＝mx0／d2。

當(dāng)z≠0，y＝d3／β時，由式 （2）第2式得

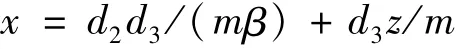
代入式（2）的第1個方程得到

由于A，B＞0，則僅當(dāng)C＜0即Re0＞1時，式（3）有一正解，從而當(dāng)且僅當(dāng)Re0＞1時，系統(tǒng) （1）存在唯一的地方病平衡點E（x，y，z）。證畢。

3 平衡點的穩(wěn)定性分析

定理2 當(dāng)R0＜1時，系統(tǒng) （1）的平衡點E（0，0，0）局部漸近穩(wěn)定；當(dāng)R0＞1時，系統(tǒng) （1）的平衡點E（0，0，0）不穩(wěn)定。

證明：系統(tǒng)（1）在E（0，0，0）處的雅克比矩陣為

其對應(yīng)的特征方程有1個實特征根λ1＝－d3＜0，另外2個特征根λ2，λ3滿足方程：

所以，當(dāng)R0＞1時，方程 （4）具有1個正實根；當(dāng)R0＜1時，方程（4）的2個根均有負實部。證畢。

定理3 當(dāng)R0≤1時，系統(tǒng)（1）的平衡點E（0，0，0）全局漸近穩(wěn)定。

證明：構(gòu)造Lyapunov函數(shù)

對L求全導(dǎo)數(shù)：

當(dāng)R0≤1時，L·≤0；當(dāng)且僅當(dāng)x＝y(tǒng)＝z＝0時，L·＝0，系統(tǒng) （1）在集合｛（x，y，z）∈D∶L·＝0｝上的最大不變集是單點集｛E｝。根據(jù)LaSalle不變性原理［18］可知，E（0，0，0）全局漸近穩(wěn)定。證畢。

定理4 當(dāng)Re0＜1＜R0時，系統(tǒng) （1）的平衡點E0（x0，y0，0）局部漸近穩(wěn)定，而當(dāng)Re0＞1時則不穩(wěn)定。

證明：系統(tǒng) （1）在E0（x0，y0，0）處的雅克比矩陣為：

易知此矩陣對應(yīng)的特征方程有1個實根：

當(dāng)Re0＜1＜R0時，系統(tǒng) （1）的平衡點E0（x0，y0，0）局部漸近穩(wěn)定。證畢。

為了證明平衡點E0和平衡點E 的全局穩(wěn)定性，首先給出以下命題。

命題1 令

可得F1（x，y）≤0，F(xiàn)2（x，y）≤0，其中（x，y）∈D。

證明：下面僅證明F1（x，y）≤0。F2（x，y）≤0類似。

1）在P01（x01，K）處的Hessian矩陣［19］為

3）在P0（x0，y0）處的Hessian矩陣為

由系統(tǒng)（1）的第1個方程可知y0＜K。因此

因此P01（x01，K）、P02（x02，K）均不是F1（x，y）的極值點。P0（x0，y0）為F1（x，y）惟一的極大值點，并在P0（x0，y0）處取得最大值，F(xiàn)1（x0，y0）＝0，所以F1（x，y）≤0。證畢。

定理5 當(dāng)Re0≤1＜R0時，系統(tǒng) （1）的平衡點E0（x0，y0，0）全局漸近穩(wěn)定。

證明：構(gòu)造Lyapunov函數(shù)，設(shè)

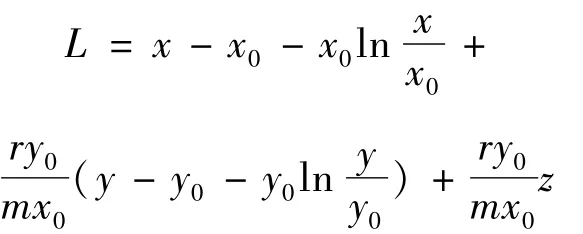
對L求全導(dǎo)數(shù)可化簡為

由命題1可得F1（x，y）≤0。當(dāng)Re0≤1時，有βy0≤d3成立，則·L≤0；并且易知系統(tǒng) （1）中｛（x，y，z）∈D：·L＝0｝＝｛E0｝；由LaSalle不變性原理知，當(dāng)Re0＜1＜R0時，E0（x0，y0，0）是全局漸近穩(wěn)定的。證畢。

定理6 當(dāng)Re0＞1時，系統(tǒng) （1）的平衡點E（x，y，z）局部漸近穩(wěn)定。

證明：系統(tǒng)（1）在E（x，y，z）處的雅克比矩陣為

矩陣的特征方程為

其中：

且有

由Hurwitz判據(jù)［17］可知，J（E）對應(yīng)的所有特征值均具有負實部。因此，系統(tǒng) （1）的平衡點E（x，y，z）局部漸近穩(wěn)定。證畢。

定理7 Re0＞1時，系統(tǒng) （1）的平衡點E（x，y，z）全局漸近穩(wěn)定。

證明：構(gòu)造Lyapunov函數(shù)，設(shè)

對L求全導(dǎo)數(shù)：

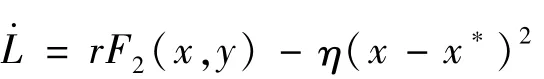
由命題1有F2（x，y）≤0，因此L·≤0；當(dāng)且僅當(dāng)x＝x，y＝y(tǒng)，z＝z時，·L ＝0；系統(tǒng) （1）在集合｛（x，y，z）∈D：·L＝0｝上的最大不變集是單點集｛E｝。根據(jù)LaSalle不變性原理可知，當(dāng)R ＞1

e0時，E（x，y，z）是全局漸近穩(wěn)定的。證畢。

4 數(shù)值模擬

模擬系統(tǒng)（1）的無病平衡點和地方病平衡點，給出時間序列圖和系統(tǒng)軌線圖。

模擬1 取r＝0．9，K＝2，d1＝0．25，d2＝0．2，d3＝0．5，m＝0．1，η＝0．01，β＝0．2，則R0＝1．286＞1＞Re0＝0．468。選取初值x（0）＝0．2，y（0）＝0．1，z（0）＝0．1，模擬平衡點E0（x0，y0，0）附近的漸近性態(tài)，如圖2所示。任取5組初始值模擬Re0＜1＜R0時系統(tǒng)的軌線圖，如圖3所示。

圖2 無病平衡點E0隨時間變化序列圖

圖3 Re0＜1＜R0時系統(tǒng)軌線圖

通過數(shù)值模擬發(fā)現(xiàn)：當(dāng)Re0≤1＜R0時，曲線隨時間變化最終趨于穩(wěn)定，所以E0（x0，y0，0）是全局漸近穩(wěn)定。

模擬2 取r＝0．4，K＝2，d1＝0．05，d2＝0．3，d3＝0．01，m＝0．3，η＝0．3，β＝0．2則R0＝1．143＞Re0＝1．067＞1。選取初值x（0）＝0．3，y（0）＝0．5，z（0）＝0．1，模擬地方病平衡點E（x，y，z）的漸近性態(tài)，如圖4所示。任取5組初始值模擬Re0＞1時系統(tǒng)的軌線圖，如圖5所示。

通過數(shù)值模擬發(fā)現(xiàn)；當(dāng)Re0＞1時，曲線隨時間變化最終趨于穩(wěn)定，所以E（x，y，z）是全局漸近穩(wěn)定。

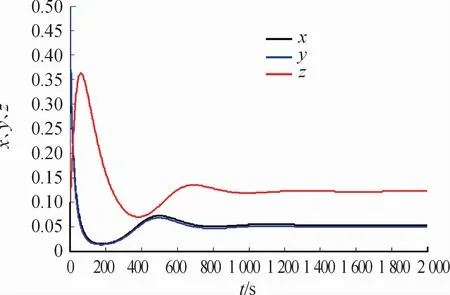
圖4 地方病平衡點E 隨時間變化序列圖

圖5 Re0＞1時系統(tǒng)軌線圖

5 結(jié)論

在考慮Logistic輸入和密度制約的情形下，分析了平衡點的存在性和穩(wěn)定性，并利用Matlab進行數(shù)值模擬。此外，同時考慮幼年和成年均受密度制約的情形或在此基礎(chǔ)上更加符合現(xiàn)實情況的疾病發(fā)生率等可作為下一步研究工作。