風電集群的儲能容量優化配置

王凱， 李喜蘭， 劉振偉 ， 鄭海林

(1.福建永福電力設計股份有限公司，福建 福州 350000；2.福州大學 電氣工程與自動化學院，福建 福州 350108)

0 引 言

要實現我國能源發展戰略目標，風力發電裝機比重必將進一步提升。然而，風電出力的間歇特性大大制約了風電的進一步發展[1]。為風電場配置儲能可以提高風電消納率以及風電場的經濟性[2-3]。

目前已有一些文獻對風電配置儲能的容量優化進行相關的研究。文獻[4]從風電功率預測誤差縮減、預測結果的合格率以及投運成本來考慮風電場的儲能配置容量。文獻[5]通過儲能的回收年份與預測誤差控制范圍來確定風電場配置儲能的最優容量。文獻[6]從減少風電場的缺電懲罰成本和棄風懲罰成本帶來的收益來優化儲能容量配置。文獻[7]提出配置合適比例容量的儲能用于平抑風電功率波動。同時，儲能作為良好的調峰和調頻資源[8-9]，文獻[10]提出了風儲系統可以通過提供輔助服務來回收成本。

現有文獻對于風電配置儲能往往僅考慮單一風電場的配置儲能情況，容易出現儲能資源浪費。此外，隨著風電并網規模的增大，電網對風電場的接納度給未來風電場發展會帶來一定的影響。

本文分析對比了各個風電場配置儲能的效益與風電集群配置儲能的效益，提出了電網對風電場并網的接納度指標，綜合考慮了風電集群配置儲能所減少偏差考核的經濟效益、參與輔助服務市場帶來的經濟效益、社會效益和儲能設施的投建以及運行維護成本。

1 風電集群配置儲能的優勢

假設風電集群中有三個風電場，參數如表1所示。

表1 各個風電場參數

考慮完全消除風電的預測偏差所需要的儲能容量，各個時刻風電場與風電集群偏差量如圖1所示。

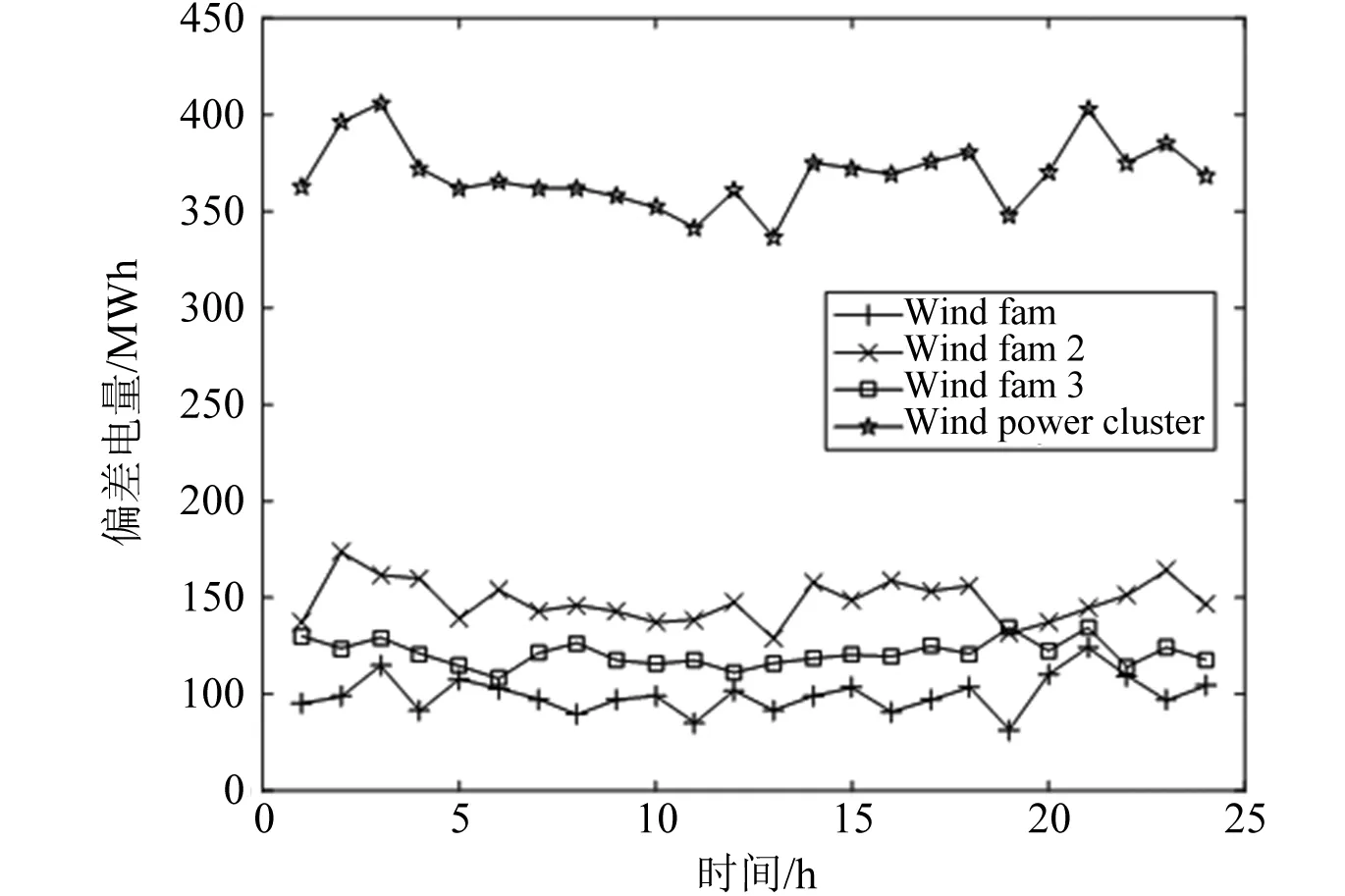
圖1 各個風電場與風電集群風電預測偏差量

在各個電場配置儲能的場景下，各風電場所需儲能容量分別為124.24 MWh、173.47 MWh和134.51 MWh。在風電集群配置儲能的場景下，所需要的儲能容量為405.94 MWh，減小了23.28 MWh的儲能配置，減少比例為5.73%，提高了風電場的經濟效益。

2 風電集群配置儲能的效益與成本

2.1 減少偏差考核的收益

當風電場的出力偏差電量超范圍時，按照偏差范圍分段計算偏差考核電量。

Rbias=∑Pbias×p1

(1)

(2)

式中:Rbias為減少偏差考核收益；Pbias為偏差考核電量；P為風電出力超發電量或欠發電量；Swind為風電場總裝機容量；p1為機組批復的上網電價。

2.2 風電場的接納度

風電功率的波動過大會降低電網對風電場的接納程度，不利于風電場規模的進一步擴大。

(3)

(4)

式中:Faccept為電網對風電場的接納度；K為總的采樣區間數；Sk為第k次采樣區間風電波動指標；Pw(k-1)、Pw(k)分別為k-1與k時刻風電出力；Pes(k-1)、Pes(k)分別為k-1與k時刻儲能動作；p為風電場每小時最大有功出力變化限值。

2.3 參與輔助服務市場的收益

參與調峰的市場主體采用分區間報價補償[11],對參與調頻的市場主體，根據調頻里程進行補償[12]。

(5)

(6)

式中:Rps為調峰帶來的收益；Rfm為調頻帶來的收益；N為時間段內計費周期的個數；p2為有償調峰申報價格；Pw(t)為風電場第t個計費周期內的實際出力；Pwe(t)為風電場參與調峰時第t個計費周期內的出力；LFM(t)為第t個計費周期內的調頻里程；Pclear(t)為調頻里程補償價格。

2.4 環境效益

環保收益為體現在燃煤機組和燃氣機組產生的污染治理成本。

(7)

式中：REP為風力發電帶來的環境效益；Cpoll為常規機組燃煤發電單位電量所產生的污染物治理費用，為了簡化計算，本文簡化為0.11 元/kWh；Pw(t)為t時刻風電配置儲能后增加的出力；T為計算周期。

2.5 儲能成本和運行損耗

由于電池容量衰減，在項目周期內更換帶來電池更換成本。儲能成本模型采用全壽命周期進行分析。

(8)

(9)

(10)

(11)

式中:Creplace為儲能電池更換成本；α為電池成本年下降比例；KR為電池的更換次數；Ces為電池的單位成本；N為電池儲能電站運營周期;L為儲能電池更換周期；CLCCNPV為儲能電站全壽命周期凈現值；CLCCNAV為儲能電站全壽命周期凈年值；CCI為儲能電站的投資成本；CCM.j為第j年的檢修成本；i為貼現率；CCD為期末退役成本。

(12)

式中：Celc為儲能運行損耗成本；Pes(t)為儲能t時刻的充電量；η為儲能的循環效率；p2為電池儲能循環損耗成本。

2.6 目標函數

用于減小偏差考核部分的儲能容量，以配置儲能后單位投資的收益最大、電網對風電接納度的提高程度為目標函數。參與輔助服務市場的儲能容量則把配置儲能后的凈收益最大化作為目標函數，通過粒子群算法進行尋優求解。

max[(Rbias+REP)/CLCCNAV+Faccept.ws-Faccept.w]

(13)

(14)

max[(Rps+Rfm)-CLCCNAV-Celc]

(15)

(16)

式中:Faccept.w為配置儲能前風電集群的接納度；Faccept.ws為配置儲能后風電集群的接納度；Sbias為用于調整偏差考核的儲能容量；Sps為參與調峰輔助服務市場的儲能容量；max(windbias)為風電的最大偏差量。

3 粒子群算法

算法流程如圖2所示。

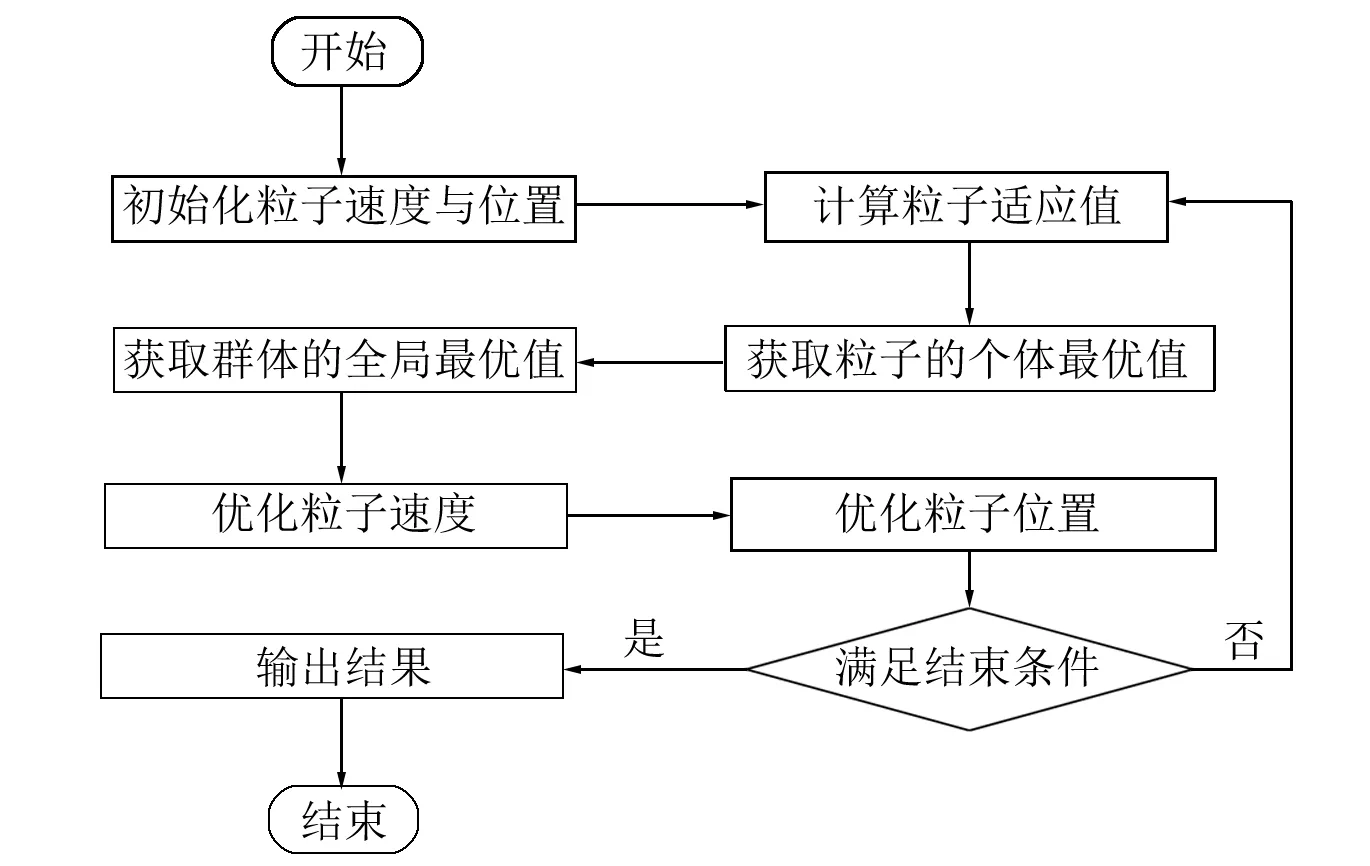
圖2 粒子群算法流程

(1) 輸入算例參數和粒子群初始參數。

(2) 計算每個粒子的適應度值，與個體極值對比，保留最優值并繼續下一次迭代。

(3) 用每個粒子的適應度函數值和全局極值對比，并更新粒子的速度和位置。

(4) 如果滿足結束條件，終止程序并輸出結果，否則返回步驟(2)繼續執行程序。

4 算例仿真分析

4.1 算例參數

本文基于某地區風電集群數據作為計劃出力曲線，假定所有預測偏差符合正態分布，風電機組以及儲能電站的參數如表2所示。

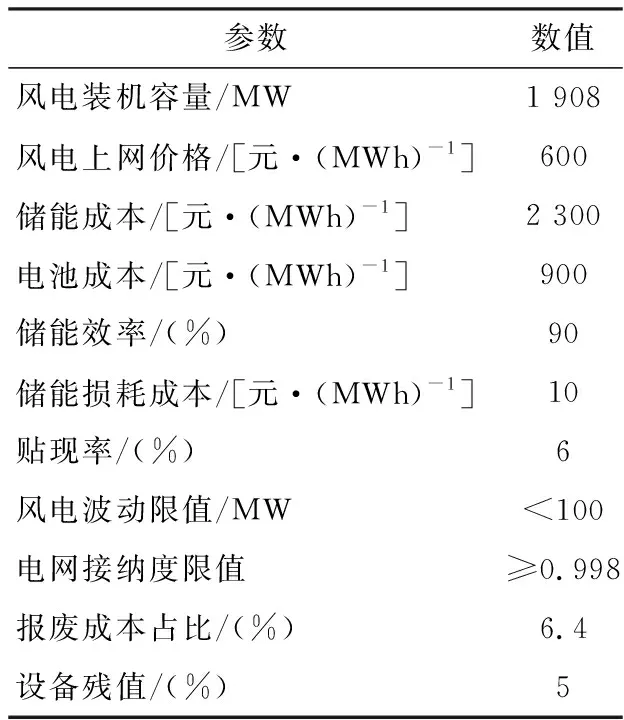
表2 算例參數

4.2 算例結果分析

(1) 針對風電集群不同的預測偏差進行了分類，不同預測精度下的最優儲能配置容量以及配置前后的接納度與投資需求如表3所示。

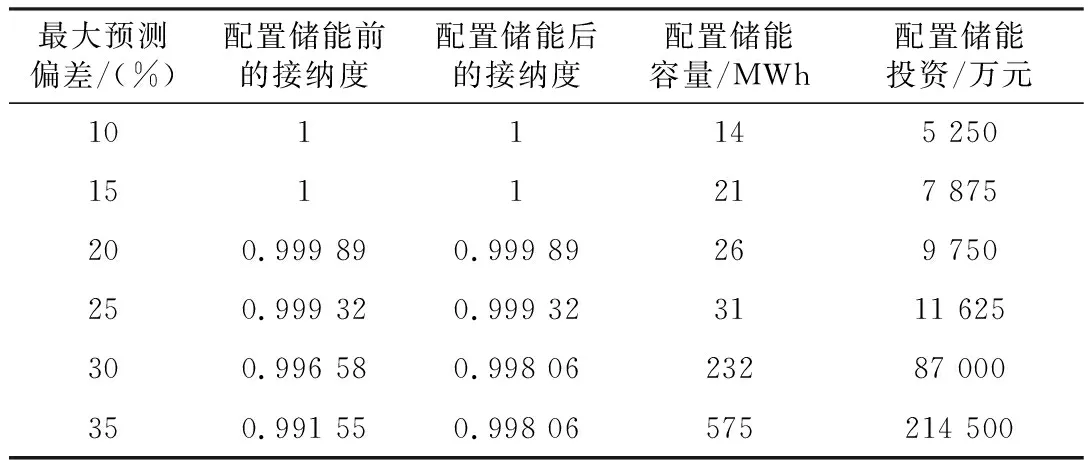
表3 用于減少偏差考核的儲能配置容量與效益

(2) 采用粒子群算法對風電集群所配置的儲能參與輔助服務市場經濟性的收斂曲線如圖3所示。當收斂到最優值時，儲能的配置容量、投資凈年值、年凈收益以及回收年限如表4所示。

表4 參與輔助服務市場儲能配置容量與效益

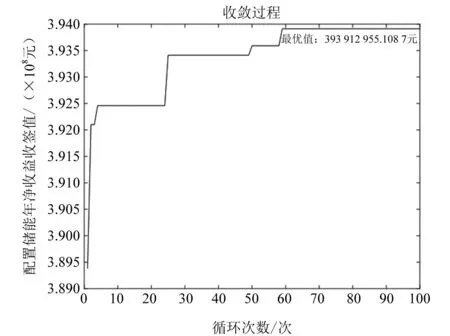
圖3 粒子群算法收斂曲線

本文研究了以風電集群配置儲能相較于分散配置儲能可以減少5.73%的儲能配置容量。當預測精度為15%時，風電場儲能最優配置比例為11.58%，回收年限為13.79年；當預測精度為20%時，風電場儲能最優配置比例為11.84%，回收年限為13.95年。

5 結束語

本文對比得出了以風電集群配置儲能的優勢，提出了風電場的接納度這一指標，綜合考慮了風電配置儲能的成本、效益以及并網后的發展，能夠更加貼近實際生活，為風電場配置儲能提供參考借鑒。