改進型憶阻退化jerk系統初值敏感的動力學和瞬態行為

張春紅 ， 朱菊香 ， 張璇

(1.江蘇聯合職業技術學院 常州鐵道分院，江蘇 常州 213011；2.南京信息工程大學 濱江學院，江蘇 無錫 214105)

0 引 言

憶阻器是一種電阻或電導可調的雙端元件，通常包含磁控和荷控兩種憶阻器。由于其非線性和記憶性，憶阻器在人工神經網絡[1-2]和圖像加密[3-4]等領域有著廣泛的應用。憶阻器作為非線性元件引入電路之后，混沌電路的動力學行為更為復雜[5]。因此，建立含有憶阻的混沌電路，分析其超級多穩定性的行為，進而闡明非線性系統對于初值的敏感性是十分重要的。

本文在退化jerk系統的基礎上，在第二方程中引入理想磁控憶阻器，提出一種改進型憶阻退化jerk系統[6]。新系統具有線平衡點，并表現出含有三種不同拓撲結構混沌吸引子的超級多穩態。此外，通過動力學特性分析，得出改進型憶阻系統的吸引子都是自激吸引子。特別是隨著初始條件的變化，新系統表現出瞬態混沌，瞬態周期甚至改變吸引盆和拓撲結構的特殊暫態行為。

1 數學模型與穩定性分析

1.1 數學模型

采用有源磁控憶阻的數學模型為:

(1)

式中:u為憶阻的終端電壓；j為憶阻內部磁通變量，j是u的積分；W(j)為與磁通量j相關的磁導率。

在退化jerk系統[6]第二方程中引入式(1)描述的憶阻，即可構建出新穎的憶阻系統，其數學模型表示為:

(2)

式中：x、y、z和w為4個狀態變量；a、b和c為原三維系統的3個控制參數。

1.2 穩定性分析

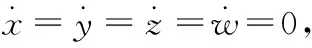
(3)

式中:η為任意實常數。不難看出I1和I2，I3和I4關于y軸對稱。

式(2)在平衡點I處的雅克比矩陣為:

(4)

相應的特征方程為：

(5)

除零特征根外，其余的特征根的勞斯陣列表如式(6)所示。

(6)

式中:γ=sgnxIsgnyI(a-1)(α+βη2)/a；μ=sgnxIsgnyI(α+βη2)。

根據勞斯判據為了避免臨界穩定狀態，系統僅考慮00，兩個實正一個實負和一個零特征根。平衡點I2和I3滿足sgnxsgny>0，一個實正兩個實負和一個零特征根。因此平衡點I1和I4為指數為1的不穩定鞍點，I2和I3為指數為2的不穩定焦點，在I2和I3附近可以形成自激吸引子的兩個渦卷。

2 無窮多吸引子的共存行為

2.1 初值敏感的動力學行為

對于式(2)，首先規定控制參數a= 0.6、b= 1.3、c=2、α=1、β=0.03，初始狀態[0，0/1，0，w(0)]。當w(0)在(-6, 8)內變化時，系統狀態分量x的分岔圖及其李雅普諾夫指數如圖1(a)和圖1(b)所示。隨著w(0)的逐漸增大，式(2)表現出復雜動力學行為，包含周期、準周期和不同吸引盆的混沌行為，以及分段倍周期分岔行為等。特別當w(0)∈(-3.697, 4.523)時，式(2)在y(0) = 0和1兩個初始條件下，呈現出對x(0)初始條件的敏感性，并且吸引子的混沌行為完全不同。

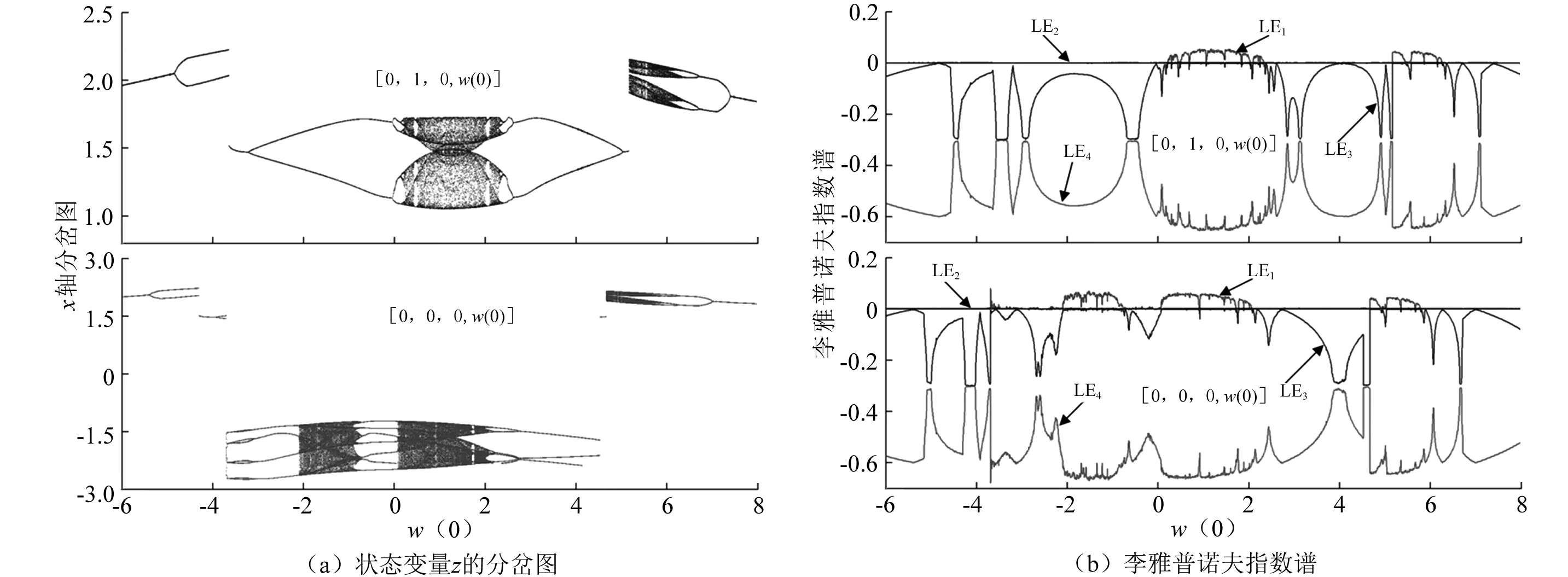
圖1 式(2)關于w(0)的動力學

2.2 無窮多吸引子

根據圖1的分岔圖，仿真獲得了在x-z平面上的若干典型吸引子相軌圖。這些吸引子有著不同的尺寸和拓撲結構，并且由于憶阻器的引入，式(2)隨著初始值的變化，所獲得的吸引子的吸引盆也是不同的，因此式(2)存在著超級多穩定性。其中，圖2(a)為三種混沌吸引子，圖2(b)為準周期和周期。初始狀態(0,0,0,0.3)為左，初始狀態(0,1,0,1)為中和初始狀態(0,1,0,6)為右的三種混沌吸引子。

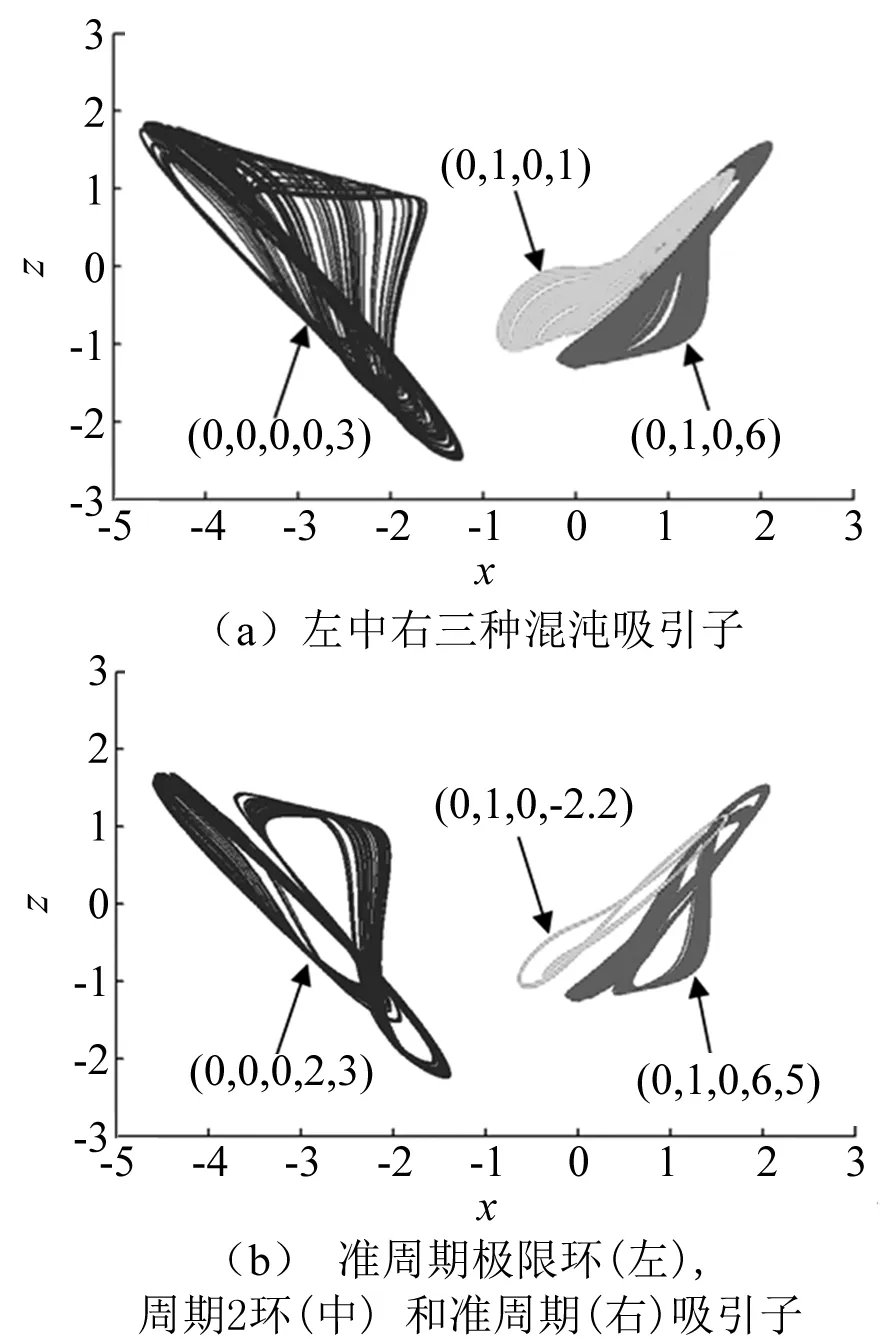
圖2 式(2)MATLAB仿真的x-z平面相軌圖

3 初值敏感的瞬態行為

對于式(2)，首先規定控制參數a=0.6、b=1.25、c=2、α=0.7、β=0.07，以初始狀態 (0，1，0，0)為例，仿真[0.5 ks，0.9 ks]和 [2.5 ks，2.9 ks]兩個不同時間段的吸引子相軌圖，由一個瞬態周期過渡到穩態混沌。特別以初始狀態(0，0，0，-2.3)為例，圖3展示了[0.2 ks，0.6 ks]和[0.9 ks，1.3 ks]兩個不同時間段的吸引子相軌圖，由圖3(a)瞬態周期過渡到圖3(b)穩態周期。

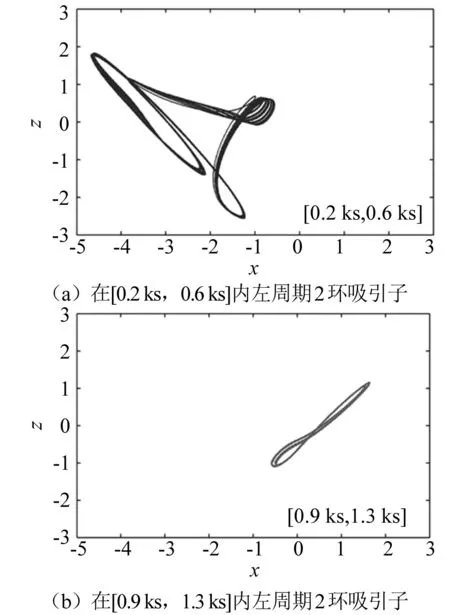
圖3 (0,0,0,-2.3)時MATLAB仿真相軌圖

4 硬件設計和PSIM仿真

構建憶阻系統式(2)的模擬電路，圖4為憶阻jerk系統的主電路。選擇時間尺度因子為k=1/(RC)，電路狀態方程可以表示為

(7)

式中:ux、uy、uz和uw為電路中 4 個電容兩端的電壓，分別對應于x、y、z和w狀態變量。為了更好地驗證系統基于初值敏感存在無窮多吸引子和復雜的瞬態行為，設計了PSIM電路,并進行仿真驗證MATLAB數值仿真結果。圖4的絕對值函數abs(·)和-abs(·)使用PSIM電路仿真軟件中的abs函數模塊和比例模塊實現。與系統(7)比較，圖4中電阻值分別為Ra=R/a=60 kΩ，Rα=R/α，Rβ=gR/β，R1=R4=R=36 kΩ。以圖3為例設定電路的初值，驗證憶阻退化jerk系統中的復雜現象。由于數學模型與電路模型的時間參數不同，圖5中的結果存在一定差異，但兩者都顯示出基于初值敏感的復雜瞬態動力學行為。

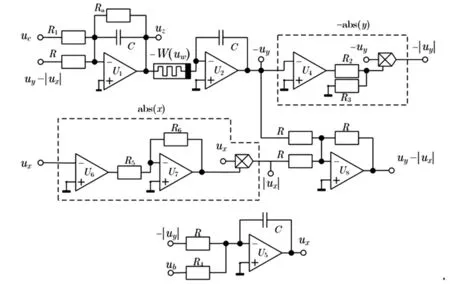
圖4 改進型憶阻退化jerk系統主電路

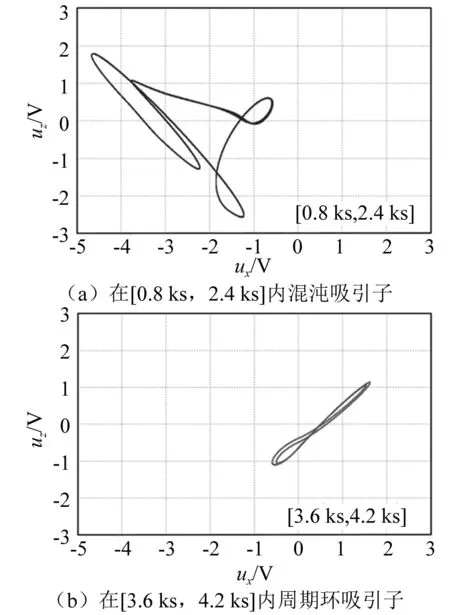
圖5 (0,0,0, -2.3)時PSIM模擬的相軌圖

5 結束語

通過在退化jerk系統中引入理想磁控憶阻器，提出改進型憶阻退化jerk系統。該憶阻系統固定系統參數條件下，通過改變系統初始狀態可以呈現出三種拓撲結構混沌、準周期和周期等超多吸引子共存。調整系統參數后，在不同的初始條件下，改進型退化jerk系統不僅存在瞬態周期和瞬態混沌，還會呈現改變拓撲結構和吸引盆的復雜瞬態混沌現象，呈現對初值敏感的復雜瞬態行為。對系統模型進行模擬電路設計，并通過PSIM電路仿真驗證了改進型憶阻退化jerk系統初值敏感的復雜動力學。