彈體非正撞擊/侵徹載荷響應的一種半經驗分析方法

王成華，楊永剛，楊 陽，劉 寧，李 磊

（北京航天長征飛行器研究所，北京，100076）

0 引 言

非正撞擊/侵徹（小攻角或大著角撞擊/侵徹）過程中彈體經受的載荷環境遠比正侵時的嚴酷和復雜，開展非正撞擊/侵徹條件下彈體的載荷強度設計和結構參數優化，是侵徹彈體工程設計的一項重要內容。數值仿真是解決非正撞擊/侵徹彈體載荷和強度計算分析的有效手段[1,2]，但由于其建模過程復雜且計算量大，不便用于方案設計和結構參數的快速優化。一套能兼顧精度和效率的非正撞擊/侵徹彈體載荷強度工程計算方法更易為設計人員接受。

美國Sandia國家實驗室和水道實驗室已在非正撞擊/侵徹彈體載荷預示方法研究方面開展過深入工作。水道實驗室的R.S. Bernard等人提出了一套基于球腔膨脹理論的非正撞擊/侵徹彈體載荷強度預示方法[3]，將球形腔膨脹理論推導出的彈體表面壓力方程直接應用于彈體表面單元、并與求解彈體終點彈道運動方程相互關聯，來確定彈體各時刻的橫向分布載荷，但其方法沒有對橫向載荷的機理和規律作進一步歸納總結，且彈體應力的計算需進一步借助有限元方法完成，方法本身仍顯復雜。基于其長期積累的試驗數據和經驗，Sandia國家實驗室的Young等人[4]總結出彈體橫向載荷與軸向載荷的經驗關系式，將經驗關系式應用于整個彈體并結合彈體終點彈道聯立求解，給出了一套計算效率較高的非正撞擊/侵徹彈體載荷強度預示方法，但由于是一種純經驗方法，缺少理論基礎。另外，上述兩套方法對彈體受撞擊/侵徹載荷后的動響應問題均未有涉及，預示結果與彈體實際的應力響應水平存有較大差距。

本文將球腔膨脹理論和彈性振動理論及經驗方法相結合，提出了一套新的彈體非正撞擊/侵徹載荷響應預示的半經驗計算方法。

1 用球形腔膨脹理論確定彈體載荷

著角（本文定義為彈軸與靶面法向夾角）和攻角均能誘導出彈體橫向載荷，二者誘導的機理不同，需要分別加以考慮。

1.1 攻角誘導出的橫向載荷

彈體質心處的速度矢量與彈軸間的夾角用總攻角α表示，彈體繞質心的轉動角速度用ω表示，忽略彈體變形產生的附加攻角，彈體剛體運動和轉動在彈體任意軸向單元i（位置坐標Xi）處誘導出的當地攻角αi具體表達式如下：

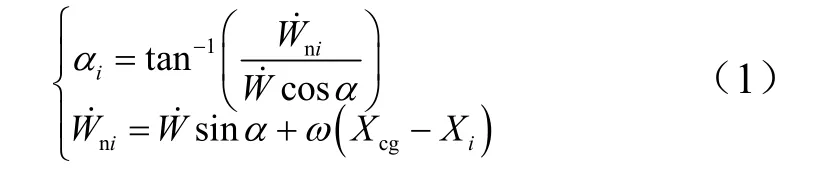
式中表示彈體速度；Xcg表示彈體質心距彈尖距離。

當地攻角αi會誘導產生垂直于彈軸方向的橫向分布載荷，這種由攻角誘導出的橫向載荷，在侵徹過程中將作用在彈體侵入靶體部分的每一處位置而不僅限于彈體頭部。將球形腔膨脹理論直接應用于非對稱受力情況下的帶攻角撞擊侵徹問題，如圖1所示。

圖1 存在攻角情況下彈體受力分析示意Fig.1 Forces Carried by Projectile under Non-normal Impact/penetrating

速度矢量投影到圖示微元法向上的速度分量為

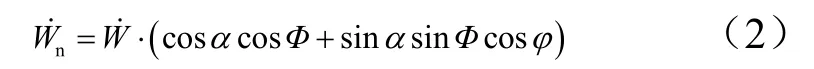
根據球形腔膨脹理論推導結果，作用在圖1所示的ds×dl微元法向上的壓力和法向面載荷分別為

法向壓力：

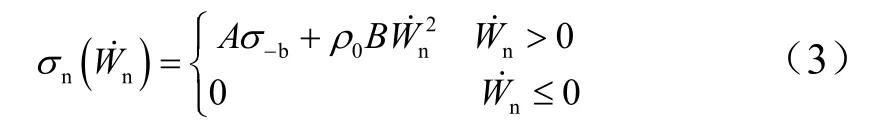
單元面載荷：

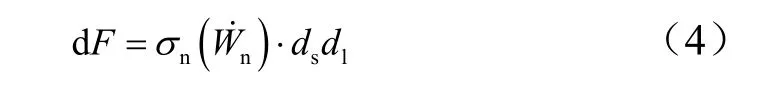
式中A為靜態阻力項系數[5]，B為動態阻力項系數，對混凝土取B=1.5；ρ0為靶板材料密度；σ-b為靶板材料無側限抗壓強度。

橫向載荷：

軸向載荷：

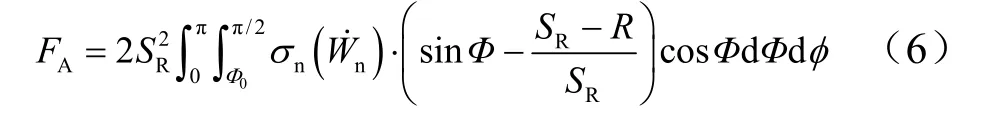
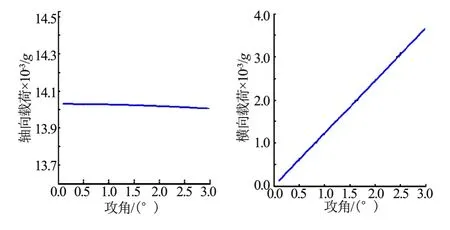
圖2 軸向載荷和橫向載荷隨攻角變化的關系Fig.2 Relation Curves Between Angle of Attack and Force

引入無量綱比例系數：

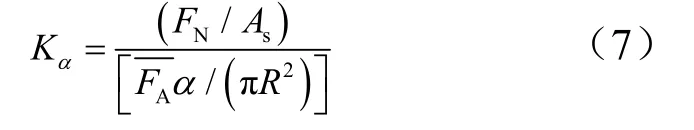
式中sA為彈體頭部側向投影面積；為侵徹平均阻力，其中Lmax為零攻角正侵極限侵徹深度，m為彈體質量，W˙0為彈體著靶初始速度。

將式（5）計算結果以式（7）無量綱形式輸出，研究發現系數Kα存在以下近似關系式：

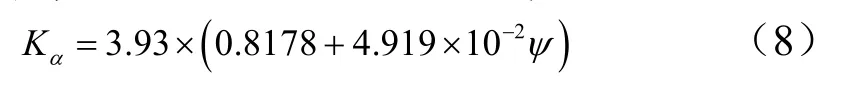
式中ψ為彈體頭部形狀因子，

基于式（7）、式（8）代表的物理意義：作用在彈體單位側向投影面積上的橫向載荷正比于單位橫截面積上的軸向載荷，并考慮到彈體撞擊/侵徹混凝土靶存在的開坑區效應，提出如下小攻角誘導彈體橫向載荷單元分量表達關系式：

式中As,i為彈體任一單元段i的側向投影面積；為開坑區損傷效應修正系數，是彈體單元段i距離靶板表面距離li的函數：

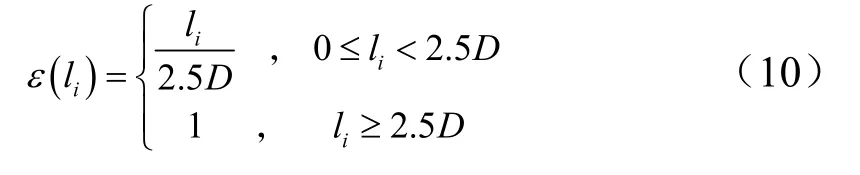
式（9）與Young等人提出的經驗公式近似，但它是基于理論和數值積分分析得到的半經驗公式，二者在系數Kα量值和形式上均不相同。計算驗證顯示式（9）不僅適用于彈體頭部，對整個彈體也適用。

1.2 著角誘導出的橫向載荷

著角誘導出的橫向載荷是由圖3所示彈體頭部Δ段上受力面不對稱和（LN-Δ）段靶板自由面效應兩方面的因素造成的。在斜侵情況下（只有著角）彈體柱段表面和靶板間相對運動的法向速度分量為0，彈體的柱段表面不會誘導出橫向力，著角誘導出的橫向載荷只需考慮彈體頭部即可。

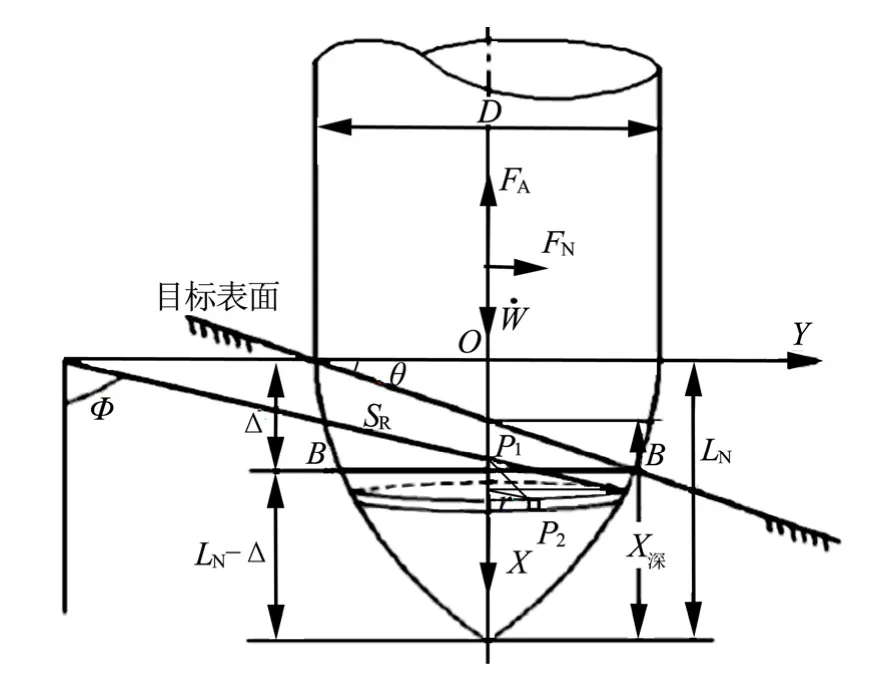
圖3 斜侵情況彈體受力分析Fig.3 Forces Carried by Penetrator in Oblique Impact

靶板作用在Δ段和（LN-Δ）段彈體表面的壓力均可采用有限尺寸介質球形腔膨脹理論確定，在考慮有限尺寸介質的自由面效應情況下，球形空腔內壁壓力簡單表達式如下[6]：

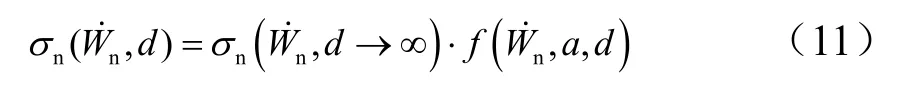
式（11）右端第1項為當介質的尺寸為無限大時球形空腔內壁壓力，可以由式（3）給出，其中的球形空腔膨脹速度 nW˙在圖3所示坐標系下具有如下形式：

式（11）右端第2項是考慮有限尺寸介質的自由面效應下的壓力損失因子，它與 nW˙、球腔內半徑a及距自由面的距離d（見圖4）有關。

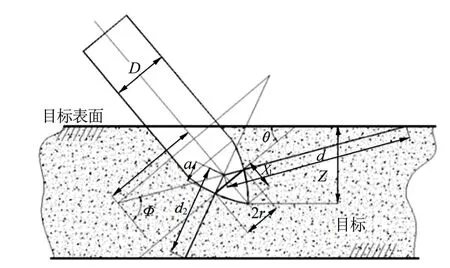
圖4 著角誘導橫向載荷自由面效應影響示意Fig.4 Free-surface Effects of Lateral Force Caused by Impact Angle

把有限尺寸介質中的球形腔膨脹理論應用于彈體非正侵情況，如圖4所示先借助解析幾何原理計算出彈頭任一表面位置處的d和a，然后代入式（11）并用式（11）替代式（3），就可以計算給出考慮自由面效應后的彈體橫向載荷與著角間的變化關系。

同樣引入一個與彈著角θ相關的比例系數關系式：

由數值積分給出的比例系數K,dθ隨侵深（用相對XCrit的無量綱變量表示）變化的關系曲線見圖5，顯示沿侵深存在兩個不同區段，兩區段分界點對應的侵深為

式中LN表示彈體頭部長度。

圖5 系數K,dθ與侵徹深度間的變化關系Fig.5 Relation Curve between Coefficient Kθ,d and Penetration Depth

式（14）顯示在XCrit以前K,dθ隨侵徹深度近似線性增加、XCrit以后則呈指數衰減并在約3XCrit侵徹深度左右K,dθ趨進于0、XCrit處K,dθ達到最大。

改變著角、靶板強度和著靶速度等參數，研究了Kθ,d對這些參數變化的敏感程度，結果顯示Kθ,d對靶板強度和著角均不敏感，但受速度的影響不可忽視，需要引入速度項修正系數Kθ,W˙來反映這種影響效應，根據數值積分結果速度項修正系數具有以下形式：

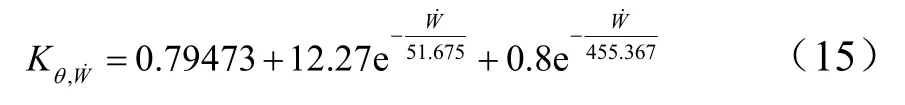
綜合考慮圖5所示隨深度變化的比例系數K,dθ和式（15）給出的速度修正系數，提出如下單元分量形式的當地著角誘導橫向力分量計算公式：

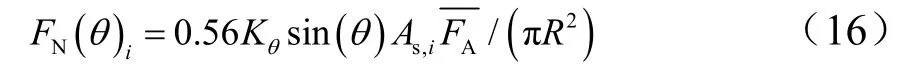
式中Kθ為合成系數，其中Kθ,d由圖5獲得；系數0.56是根據數值驗證情況確定的修正系數。

2 撞擊/侵徹載荷作用下的彈體結構響應計算

撞擊侵徹過程中彈體會發生彈性響應變形，彈體的應力計算需要考慮撞擊侵徹過程中的沖擊響應放大。將式（9）、式（16）與彈體終點彈道運動方程求解過程相關聯，首先確定撞擊/侵徹各個時刻點的彈體載荷分布，再通過彈性振動理論中的模態疊加法，就可以確定出彈體在撞擊/侵徹沖擊載荷作用下的響應放大情況。

彈體長細比較大時，可以將彈體簡化成一個等截面梁模型，撞擊/侵徹過程中彈體在橫向分布激勵載荷f(x,t)作用下的結構變形y(x,t)根據模態疊加法有如下形式解：

式中ωn,r為彈體第r階模態頻率；ξ為阻尼比系數；ωd,r彈體第r階諧振頻率，為廣義力，為彈體長度。

撞擊/侵徹條件下彈體約束方式為兩端自由-自由狀態，彈體的各階固有頻率ωn,r和歸一化振型可以通過試驗或計算獲得，對于均質等截面梁可以通過查表獲得[7]，將獲得的Yr（x）和式（18）確定的代入式（17），即可獲得各個時刻的彈體結構變形y(x,t)，彈體各截面的彎矩可通過下面的差分方程求解：

由M（x,t）進而獲得由橫向載荷引起的彈體彎曲響應應力。

注意到軸向載荷FA(t)只作用于彈體頭部，可以將其簡化為集中載荷作用在彈尖位置處、并忽略阻尼比系數影響，彈體軸向彈性響應加速度具有如下簡單形式：

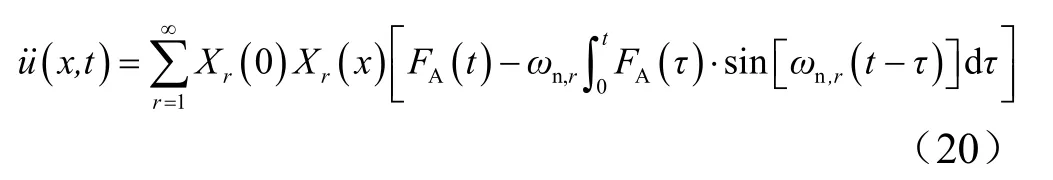
3 彈體撞擊/侵徹過程的運動學求解

需要建立非正撞擊/侵徹彈體運動微分方程并與第1節、第2節計算過程聯立求解，最終確定撞擊/侵徹過程彈體載荷變化以及彈體結構變形響應的時間歷程。圖6為非正撞擊侵徹彈體受力及運動模型。

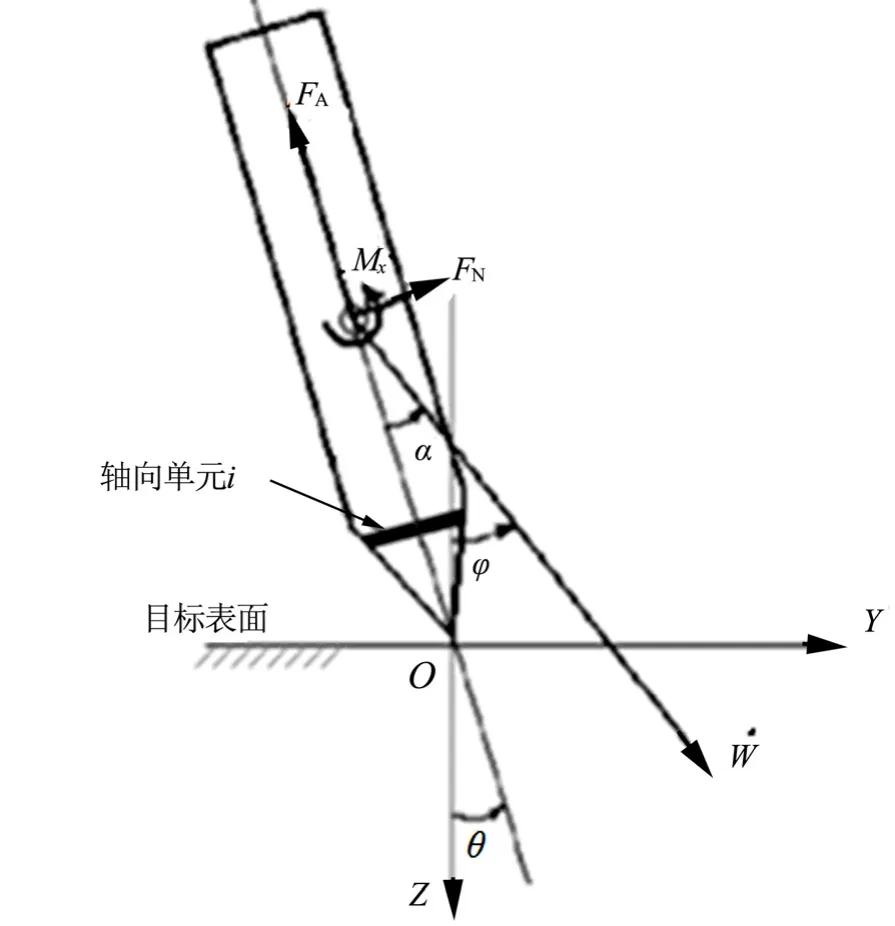
圖6 非正撞擊侵徹彈體受力及運動模型Fig.6 Terminal Ballistics and Stress Model for Penetrator in Non-normal Impact/penetration

彈體質心運動方程形式為

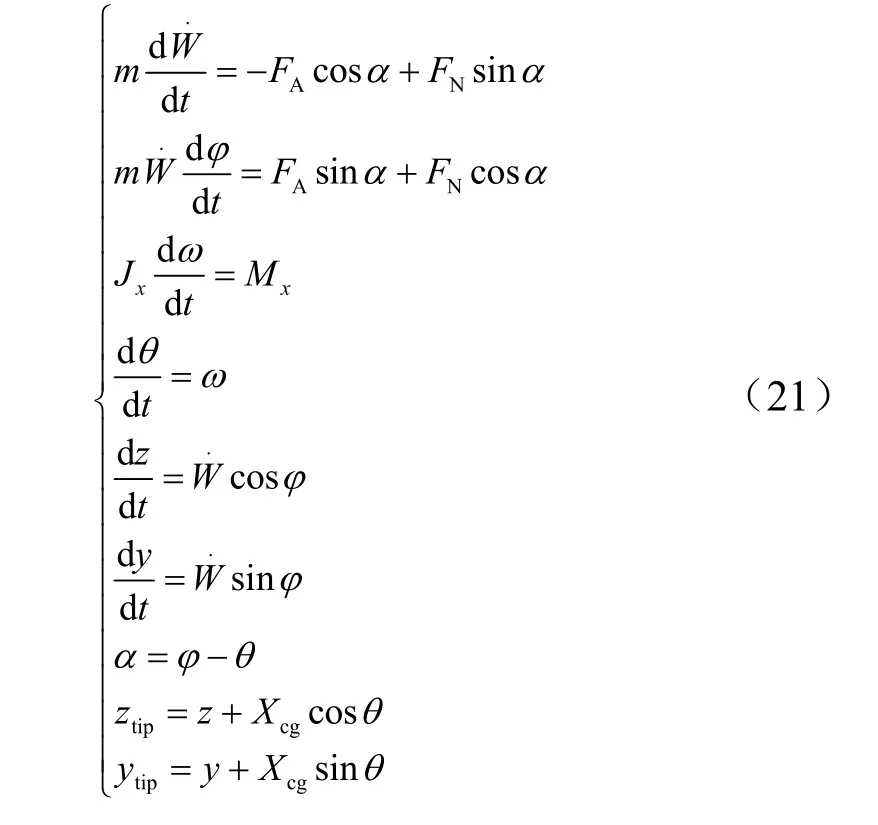
式中Jx為彈體繞質心轉動慣量；ytip，ztip為彈尖位置坐標；y，z為彈體質心位置坐標；AF為彈體軸向阻力；NF為橫向載荷。

給定彈體初始著靶速度、彈著角和攻角，借助上述微分方程就可以求解出撞擊侵徹過程任一時刻的彈體運動學參數，彈體軸向阻力和橫向載荷根據彈體所對應時刻的侵深和姿態、由第1節方法計算給出。

4 半經驗計算方法的數值仿真驗證

基于本文半經驗方法，對多個彈體算例侵徹過載和應力進行預示，從彈體過載/應力變化時間歷程和最大峰值方面，進行了與LS_DYNA3D數值仿真結果間的對比驗證。圖7表示了彈體最大應力時間歷程變化。

以某縮比實驗彈為例，著靶初始條件：攻角3°、著角0°、著靶速度600 m/s，靶板混凝土材料無側限抗壓強度30 MPa。數值仿真給出的彈體受力最嚴重部位的應力變化曲線見圖7a，對應的彈體最大應力為-5322 MPa；本文方法計算給出的應力變化曲線見圖7b，對應的彈體最大應力為-4998 MPa，最大應力量值上與仿真結果接近。應力曲線的變化規律上，本文方法模擬出了彈體在穿靶過程中出現的多個應力響應峰，峰值發生的時刻與仿真結果基本吻合。

表1為小攻角撞擊混凝土靶彈體侵徹過載和最大應力，表2為大著角撞擊混凝土靶彈體侵徹過載和最大應力。進行了小攻角和大著角多種子樣情況下彈體過載和應力峰值與數值仿真結果的對比，表1和表2結果顯示本文方法具有較廣泛的適應性，與數值結果相比彈體應力預示結果的相對誤差基本能控制在30%左右。

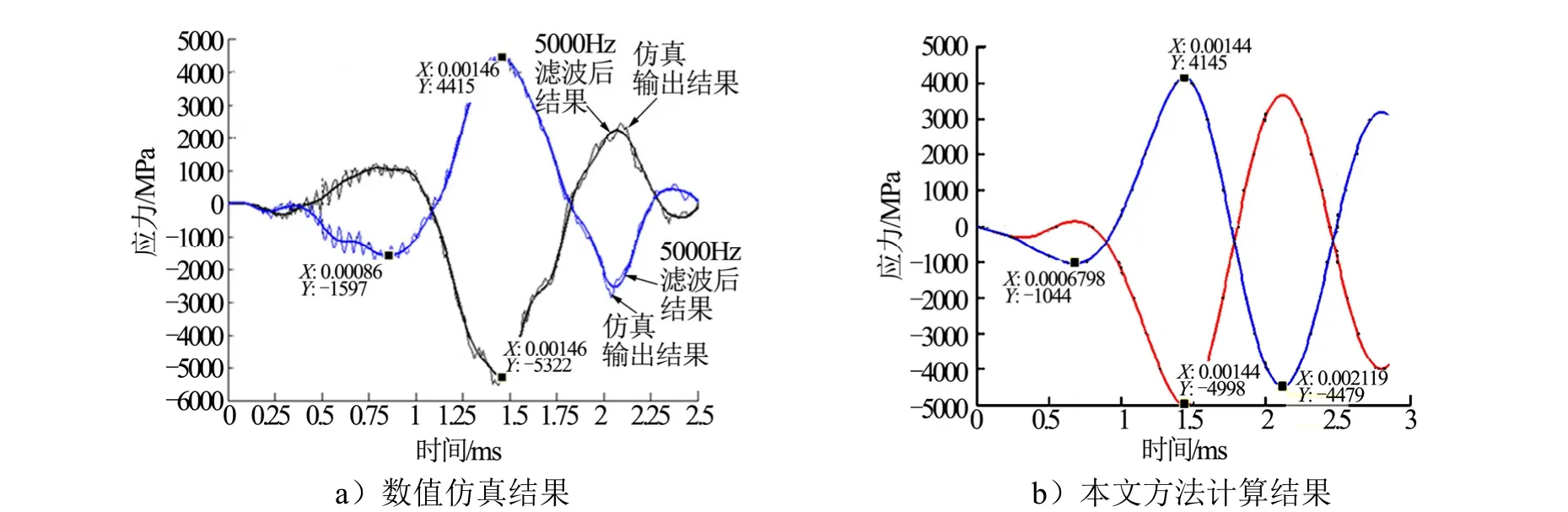
圖7 彈體最大應力時間歷程變化Fig.7 Maximum Stress Time History of Penetrator

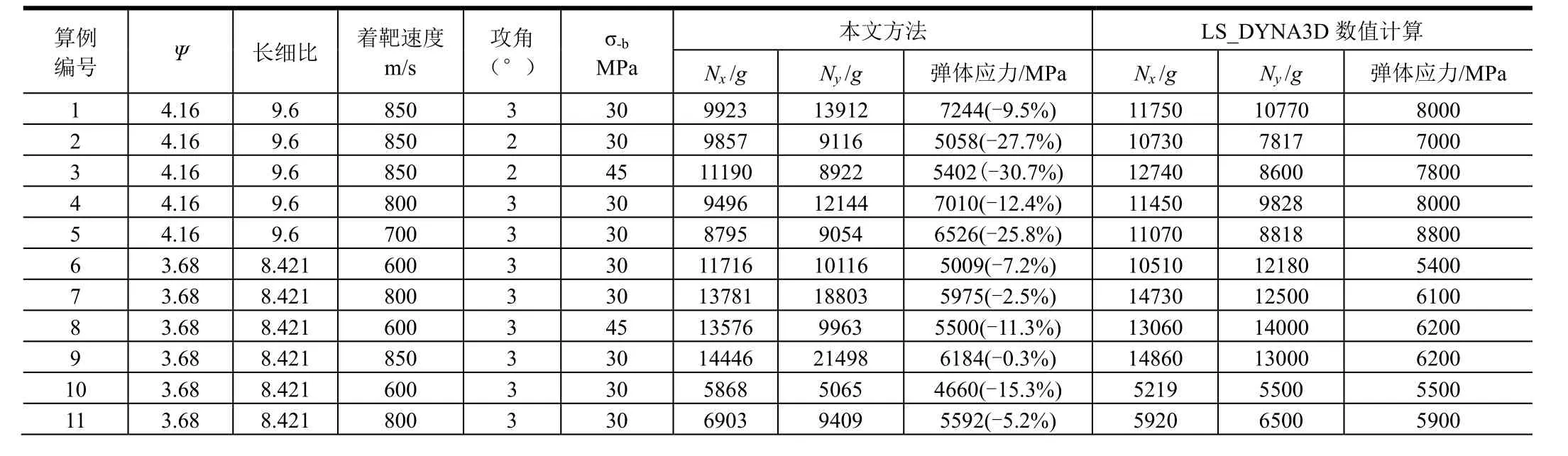
表1 小攻角撞擊混凝土靶彈體侵徹過載和最大應力Tab.1 Aeceleration and Maximum Stress of Projectile Penetrating into Concrete Targets with Small Angle Attack

續表1

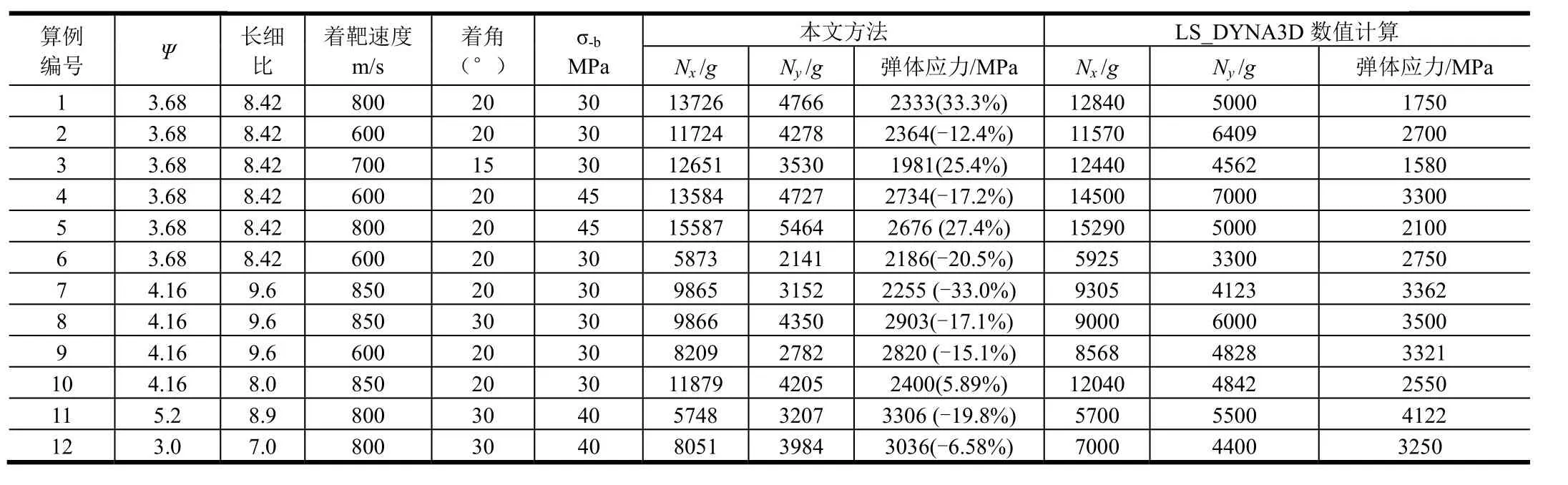
表2 大著角撞擊混凝土靶彈體侵徹過載和最大應力Tab.2 Aeceleration and Maximum Stress of Projectile Penetrating into Concrete Targets with Large Impact Angle

5 結 論

通過將球形腔膨脹理論的應用范圍推廣到彈體非正撞擊/侵徹情況，本文對非正撞擊/侵徹過程攻角和著角誘導載荷的機理以及靶板自由面效應的影響特性等進行了分析，提出了一套建立于理論分析并輔之以數值驗證的彈體非正撞擊/侵徹載荷響應半經驗計算方法，將基于這套方法得到的彈體連續分布時變載荷作用于彈體上，采用彈性振動模態疊加法，得到了非正撞擊/侵徹載荷作用下彈體的沖擊響應時間歷程。

與數值仿真結果的對比驗證情況表明：本文方法能夠模擬出彈體載荷和應力沿終點彈道的主要時間歷程變化規律，沖擊響應曲線的特征（峰值個數、大小及發生時刻等）和峰值量值均與仿真結果一致，且方法具有較廣適應性，彈體應力預示結果的相對誤差基本能控制在30%左右。