基于蒙特卡洛法的拋錨撞擊海管概率分析

尹豐,劉宇,鄧宇林,劉延波

(1.中海油研究總院,北京 100000；2.哈爾濱工程大學 船舶工程學院，哈爾濱 150000)

近些年，海底管道的鋪設數量逐漸增加，近海航運和漁業快速發展，由落錨、拖錨等第三方因素引起的管線損傷事故頻發，危害極大[1-2]。挪威船級社和中海油能源發展股份有限公司提出了一種海上墜物對海底管道撞擊概率的計算方法[3-4]，該方法的計算過程復雜，精確度依賴于計算步長的選取，當步長小于有效撞擊寬度時將不再適用。蒙特卡洛方法[5]也稱統計模擬法、統計試驗法，適用于求解不確定性問題，在金融工程學、生物醫學等領域應用廣泛。考慮采用蒙特卡洛方法，建立拋錨統計試驗模型，實現對該問題的求解。利用上述3種方法，分別對某一條件下船舶拋錨對海底管道的撞擊概率進行計算，探究船舶拋錨點到海底管道水平距離、海底管道外徑對撞擊概率的影響，對比計算結果，驗證蒙特卡洛方法的準確性和適用性。

1 船舶拋錨

1.1 船舶拋錨作業

拋錨是船舶最基本的操縱作業，涉及到很多專業技能，如果操作不當，很容易發生走錨、斷鏈、丟錨等狀況，需要慎重對待[6]。船舶拋錨可分為普通拋錨和應急拋錨。

普通拋錨主要包括深水拋錨、大風浪中拋錨、急流中拋錨，以及錨地擁擠、順水或進車時拋錨等。急流中拋錨一定要頂流拋錨；在擁擠的錨地拋錨時，應注意控制車速不能快，轉向時應適當加車以增加轉頭力矩；順水拋錨應在有足夠的旋回范圍的寬敞水域進行拋錨。

應急拋描是將錨直接從錨鏈孔丟入海中，一般是在緊急情況下使用，諸如在大風浪中采用頂浪滯航法，用以增加船舶漂泊阻力、控制艏方向或者采用拋描拖行用以減小船速，保證船舶航行安全。應急拋錨作業時，錨的觸底速度通常會大于正常拋錨時錨的觸底速度，且會加大錨對海底的沖擊力[7]。

1.2 船錨運動模型

船舶拋錨后，船錨在海水中的下落過程存在漂移現象，如圖1，假定漂移服從正態分布，表示為

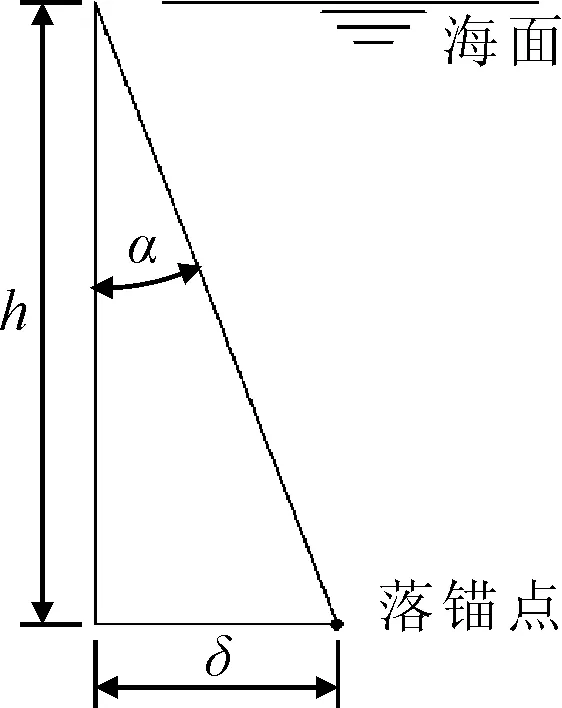
圖1 船錨的漂移現象示意

(1)

δ=htanα

(2)

式中：p(x)為錨到達海底落錨點時與拋錨點水平距離為x的概率；x為落錨點與拋錨點之間的水平距離，m；δ為橫向偏移，m；h為落錨點水深，m；α為偏移角，與錨的形狀、質量有關，rad。

2 拋錨對海管的撞擊概率計算方法

2.1 現有方法

挪威船級社和中海油提出的海上墜物對海底管道撞擊概率的計算方法，首先確定船錨落在某一區域內的概率，并根據區域內有效撞擊面積占區域總面積的比值，計算出船錨會撞擊此段管道的概率，最后將所有區域內船錨撞擊管道的概率累加，即為海域內船舶拋錨對海底管道的撞擊概率。

2.1.1 區域內落錨概率

基于船錨在海水中的運動模型，落錨點位于以拋錨點為圓心，半徑為r的圓內的概率為

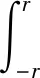
(3)

如圖2，以拋錨點為圓心，將海域劃分為等寬的圓環，圓環寬度即為步長，則落錨點位于內徑為ri、外徑為ri+1的圓環內的概率為

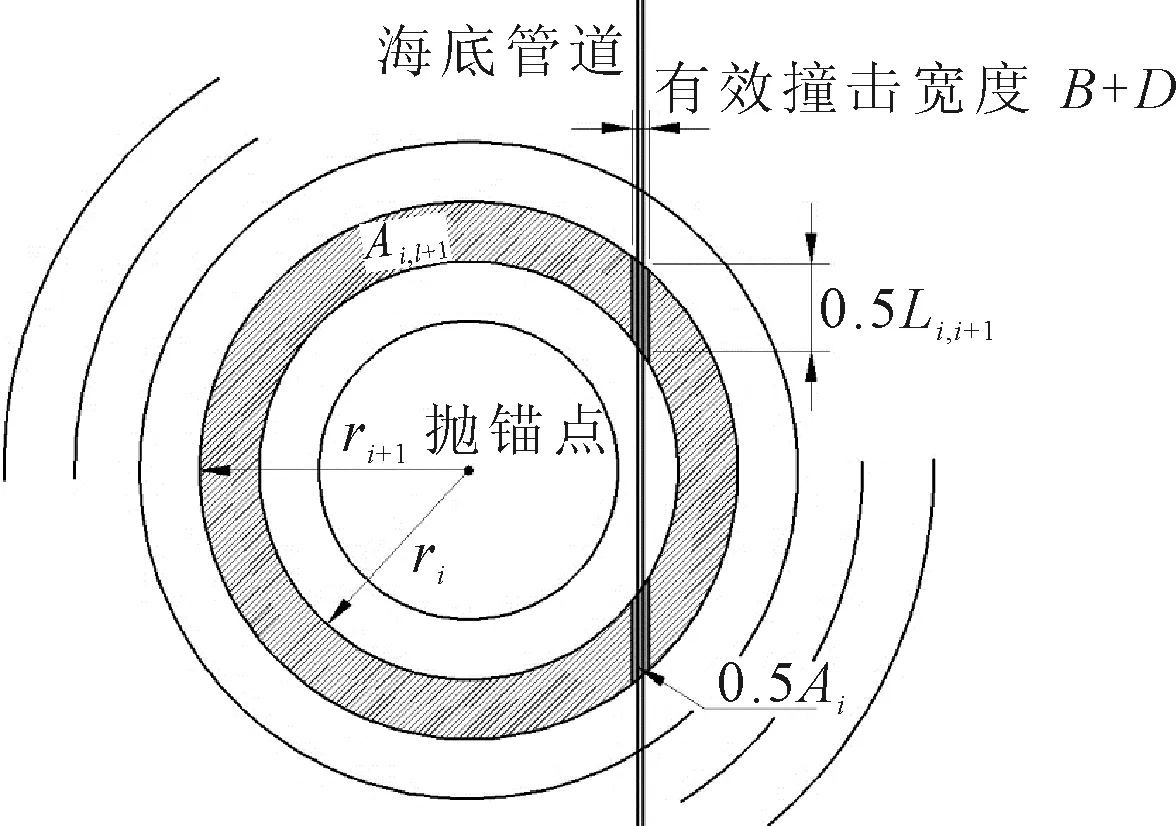
圖2 圓環內撞擊概率示意

pi,i+1=p(x≤ri+1)-p(x≤ri)=pi+1-pi

(4)

2.1.2 圓環內船錨撞擊管道的概率

如圖2，在內徑為ri、外徑為ri+1的圓環內，假定落錨概率相等，則船錨撞擊管道的概率可表示為

(5)

Ai=Li,i+1(D+B)

(6)

(7)

式中：phit,i,i+1為船錨撞擊圓環內管道的概率；Ai為圓環內的有效撞擊面積，m2；Ai,i+1為圓環的面積，m2；Li,i+1為圓環內海底管道的長度，m；D為海底管道的外直徑，m；B為船錨寬度，m。

2.1.3 海域內船錨撞擊管道的概率

對于整片海域，船舶拋錨后，船錨撞擊海底管道的概率Phit為

(8)

2.2 現有方法的改進

現有的拋錨對海底管道撞擊概率的計算方法因假定圓環內落錨概率相等，故圓環步長越小精度越高，但當步長小于有效撞擊寬度時，無法計算有效撞擊面積，現有方法將不再適用。假定圓環的步長無限小，以圓弧代替圓環，通過積分累加各個圓弧上有效撞擊長度得到拋錨對管道的撞擊概率，提高計算精度，實現對現有方法的改進。如圖3，以拋錨點為圓心的部分圓與有效撞擊寬度存在交叉的部分，交叉部分的長度即為有效撞擊弧長，以y為變量對有效撞擊弧長進行積分，可得船舶拋錨對海底管道的撞擊概率Phit為

圖3 積分改進現有方法示意

(9)

2.3 蒙特卡洛方法

采用蒙特卡洛方法求解某個問題時，首先要建立一個與問題相對應的概率模型或隨機過程，使其數或數字特征等于問題的解；然后通過對模型或過程的觀察、抽樣試驗來計算這些參數或數字特征。

以式(1)為基礎，進行n次拋錨試驗，模擬船錨的漂移現象，記錄船錨與管道發生碰撞的次數，將其與總試驗次數n的比值作為在此條件下船舶拋錨對海底管道的撞擊概率。

具體過程：首先以拋錨點為原點建立極坐標系，確定有效撞擊范圍，分別生成n個服從式(1)分布形式的隨機數和n個在區間[0,2π]之間均勻分布的隨機數，一一對應組合成為n個極坐標點，統計在有效撞擊范圍內的點的數量，即為船錨與管道發生撞擊的試驗次數。

3 算例

假設在某平均水深為100 m的海域，海底鋪設1條外徑為D的輸油管道，長度無限長。在距離管道水平距離為x處，有1船舶即將拋錨。船錨為霍爾錨[7]，質量為750 kg，錨干長度1 425 mm，錨的寬度為1 000 mm。

3.1 現有方法

采用現有方法，計算船舶拋錨對海底管道的撞擊概率，工況設計見表1。計算結果見圖4。

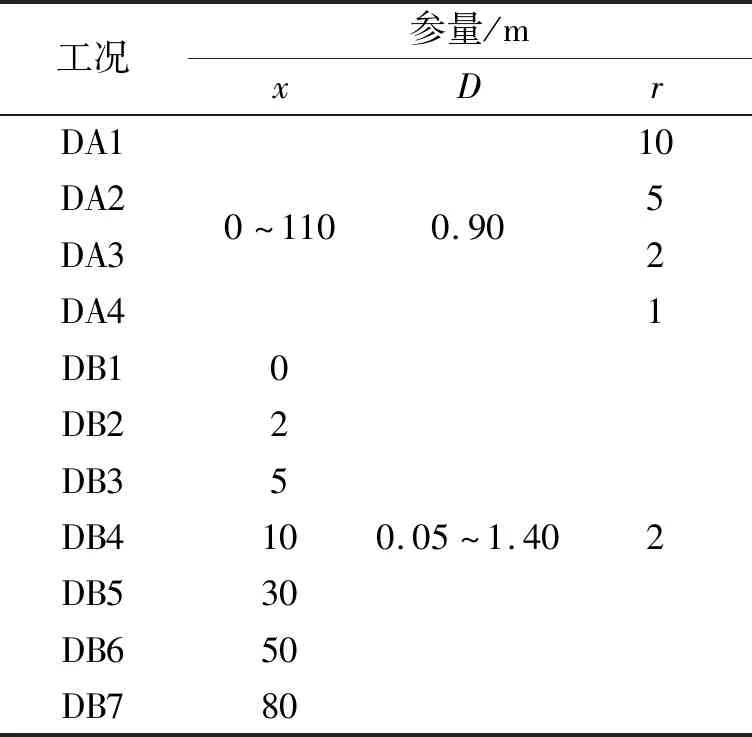
表1 現有方法計算撞擊概率設計工況

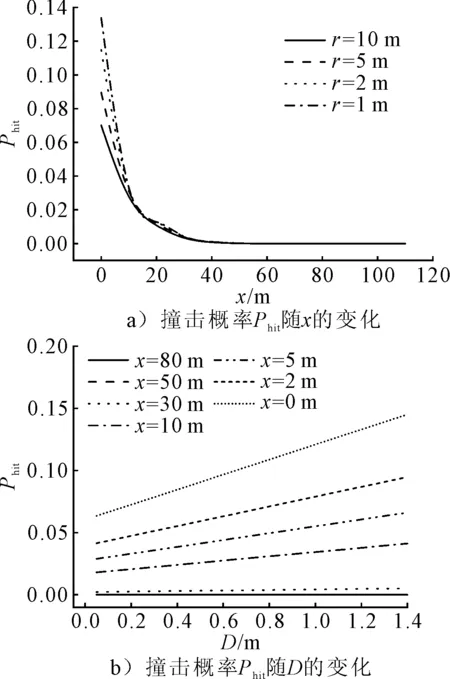
圖4 拋錨對管道撞擊概率現有方法計算結果

由圖4可知，當船舶在管道正上方拋錨時，船錨撞擊管道的概率最大，隨著x的增大，撞擊概率迅速下降為0，在撞擊概率較大的位置，由步長引起的誤差較明顯；撞擊概率與管道外徑呈線性關系，隨著管徑的增加，撞擊概率也增大，這是因為在單個圓環范圍內，假定各點落錨概率相等，管徑的增加等價于有效撞擊面積的線性增加，因而撞擊概率與管徑之間呈現線性關系。

3.2 改進后的方法

通過積分對現有方法進行改進，計算船舶拋錨對海底管道的撞擊概率，工況設計見表2。

表2 積分方法計算撞擊概率設計工況

3.3 蒙特卡洛方法

采用蒙特卡洛方法，進行船舶拋錨的統計試驗，計算船錨對海底管道的撞擊概率，工況設計見表3。

表3 蒙特卡洛方法計算撞擊概率設計工況

由圖5可知，隨著隨機點數n的增加，撞擊概率Phit隨x變化曲線逐漸趨于平緩，當n=9×105時，該曲線與n=9×106的曲線幾乎完全重合，可以認為此時的隨機點數量已經足夠使計算結果達到合適的精度；撞擊概率Phit與管道外徑D呈微弱的非線性關系，這是因為隨著管徑的增加，船錨落在新增撞擊范圍內的概率與落在原撞擊范圍內的概率不同。

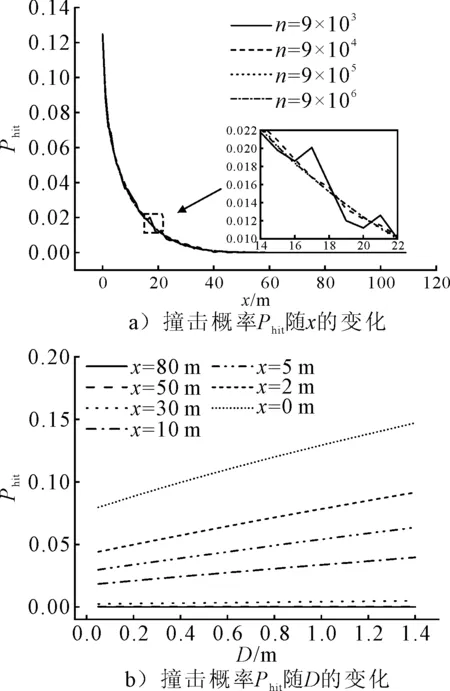
圖5 蒙特卡洛法計算拋錨對管道撞擊概率

3.4 對比分析

分別將工況DA3、DA4、JA1、MA3和工況DB3、JB3、MB3的計算結果進行對比，見圖6。

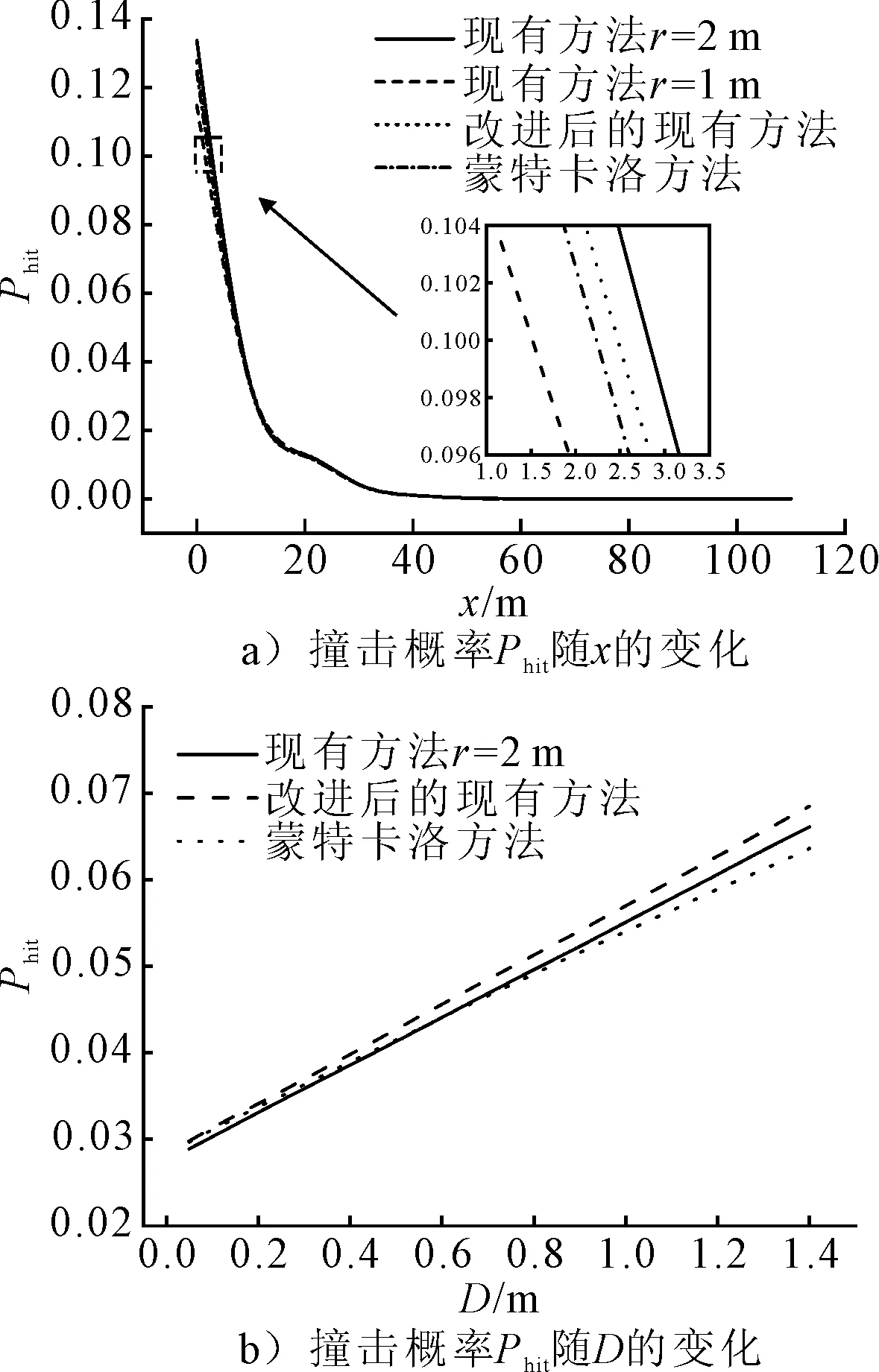
圖6 不同方法計算拋錨對管道撞擊概率

3種方法計算得出的Phit隨x、D變化趨勢基本一致；在x<10 m時，蒙特卡洛方法計算得出的Phit略小于現有方法改進后計算出的Phit，兩者又同時介于現有方法步長r=1 m和r=2 m時的計算結果之間；當x≥10 m時，不同方法的計算結果差距不明顯，這是因為，隨著x的增大，Phit的數值迅速減小，不同方法計算結果的絕對差值也迅速減小。

4 結論

對現有方法進行改進或利用蒙特卡洛方法都能較好地反映船舶拋錨對海底管道的撞擊概率變化特性；考慮計算的復雜程度等因素，蒙特卡洛方法更具優越性；可以將蒙特卡洛法應用于危險區域的拋錨預警和海上禁錨區的設置等方面。