彎道航行時集裝箱側翻落水事故防范
陳志飚,朱顯玲,張帆,侯超
(1.中國船級社武漢規范研究所,武漢 430022;2.武漢船舶職業技術學院,武漢 430050;3.中國船級社重慶分社,重慶 401121)
2017年8月28日,某集裝箱船下行至長江干線長壽水域,在彎道航行時發生集裝箱落水事故[1]。根據調查結果,本次事故主要原因[2]是船員操作失誤,在彎道航行時引航操作不當致使船舶駛入泡漩,之后又未能及時減速和正確操舵,最終造成船體傾斜、綁繩(綁扎鋼絲繩)崩斷,船上載運的24個集裝箱落水。為了預防再次發生類似事故,收集該事故的數據資料,分析事故的力學機理和影響因素,提出改進和防范措施。
1 事故過程
事發時船舶處于夜航下行狀態,航速較快(24 km/h),集裝箱落水過程可簡化為3個階段。
1)船舶左轉,舷外水漫上甲板,見圖1a)。
2)漫上甲板的舷外水持續增多,淹至貨艙艙口圍板根部,集裝箱相對船體右傾,集裝箱綁繩繃緊,見圖1b)。
3)集裝箱右傾加劇,最終側翻落水(見圖1c)),從落水后的綁繩狀態(見圖1d))可推知,綁繩在落水前已經崩斷。

圖1 右舷集裝箱落水過程截圖及示意(截圖來自右舷看向尾的監控視頻,示意圖為尾視圖)
此外,根據貨艙內未進水這一事后檢查結果可知,事故中舷外水并未淹沒貨艙艙口圍板。
2 力學分析
2.1 事故時的力學模型
該船為典型的內河集裝箱船,集裝箱系固采取整垛八字綁扎[3](見圖1b)和圖2),左右舷綁繩緊貼最外側延伸至頂部,即規范[4]中規定的頂部交叉綁扎。以最先側翻的集裝箱行(即BAY,圖1a)和1b)中綁繩所在位置)作為研究對象,所有集裝箱為40 FEU,積載情況見圖2,圖中數字為單箱質量,t。

圖2 落水集裝箱堆垛的積載與綁扎
不同于碼頭堆裝時集裝箱側翻落水[5],針對船舶彎道航行中集裝箱相對于船體開始側傾的瞬間,建立力學分析模型,見圖3。
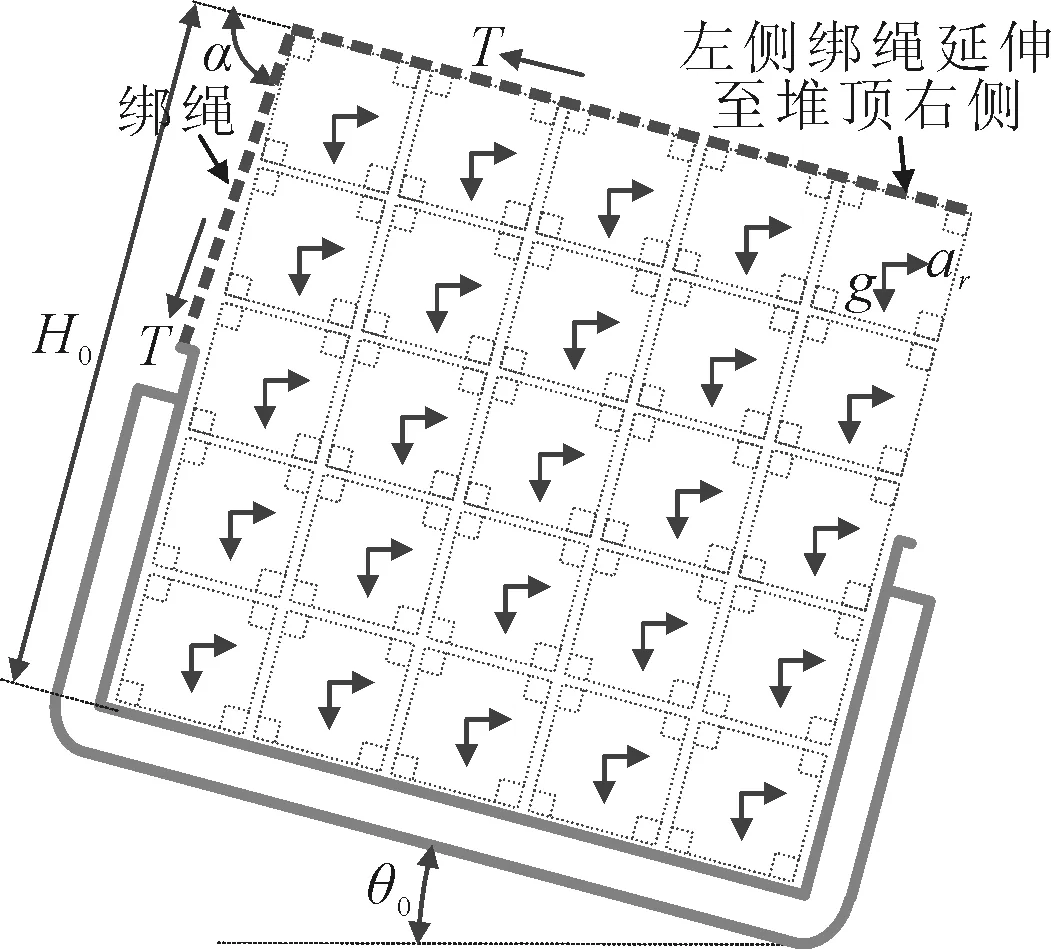
圖3 落水集裝箱堆垛的力學模型
1)集裝箱與船舶一起右傾,對地的傾角與船舶傾角θ0相同。
2)船舶急速左轉,集裝箱承受離心慣性力,離心加速度ar。
3)集裝箱承受重力,重力加速度g。
4)據船首監控錄像,事發時風平浪靜,因此忽略風浪等引起的船舶運動影響。
5)各列集裝箱之間頂層有橋鎖連接,列間存在相互作用力,整行視為一體,由綁繩提供拉力T抵抗集裝箱堆垛右傾,綁繩從右側頂層集裝箱橫穿左側頂層集裝箱最后連接至左舷艙口,左舷側部分的綁繩與船舶基平面夾角α。
2.2 側翻堆垛的受力分析
為防止集裝箱側翻落水,需要防止綁繩崩斷,而綁繩崩斷意味著其承受的負荷(拉力)大于本身的許用負荷。因此,需要分析確定集裝箱側翻時綁繩承受的拉力。
如圖3所示,假定綁繩不會崩斷,則該行集裝箱堆垛首尾兩端的綁繩拉力T產生的抵抗力矩等于集裝箱堆垛的側傾力矩,即:
2TH0cosα=∑Mi
(1)
式中:H0、α見圖3,按實船作圖測量得13.095 m和87.5°;Mi為堆垛中單個集裝箱的側傾力矩。
Mi=Gi(gsinθ0+arcosθ0)hi-
(2)
集裝箱層間未使用扭鎖,下層箱不會給上層箱提供拉力以幫助上層抵抗側傾,因此取Mi≥0;Gi為單個集裝箱箱重(質量);hi為集裝箱中心至艙底的垂直距離,從積載圖上測量;b為集裝箱寬度,取2.438 m;θ0為圖3所示橫傾角,具體數值未知;g為重力加速度,取9.81 m/s2;ar為離心加速度。
(3)
其中:Vm為轉彎航速,按事故資料取24 km/h;R為轉彎半徑,按該船試航資料取127.6 m。
依據式(1),T為
(4)
分析式(4)(2)(3)可知,為計算確定綁繩拉力T,尚需確定橫傾角θ0的具體數值。
2.3 側傾時橫傾角的確定
該事故船型深5.2 m,型寬17.2 m,貨艙寬12.7 m,甲板梁拱0.2 m,圍板頂緣距基線6.2 m,事發時船舶吃水為3.9 m,舷外水漫過了主甲板,超過了艙口圍板根部,但貨艙尚未進水(未超過艙口圍板頂緣),據此可測算得船舶橫傾角處于12.3°~19.9°之間,見圖4。
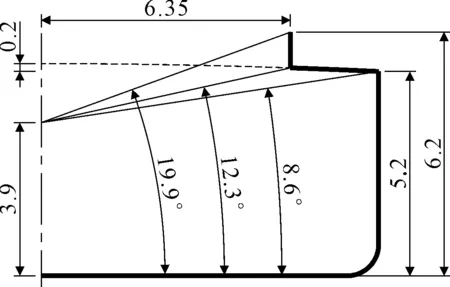
圖4 橫傾角測算圖(單位:m)
因為無法觀測到舷外水的具體位置,所以無法測算船舶橫傾角的準確值,本文分析計算時取θ0=12.3°,此時計算所得的綁索拉力為最小值。
2.4 綁繩拉力計算與崩斷判定
將集裝箱箱重(見圖2)和測算所得橫傾角θ0等參數代入式(2),可得單個集裝箱的側傾力矩,見表1,與圖2對應。表1中正值表示如無綁繩拉力約束則會發生側傾,負值則相反。
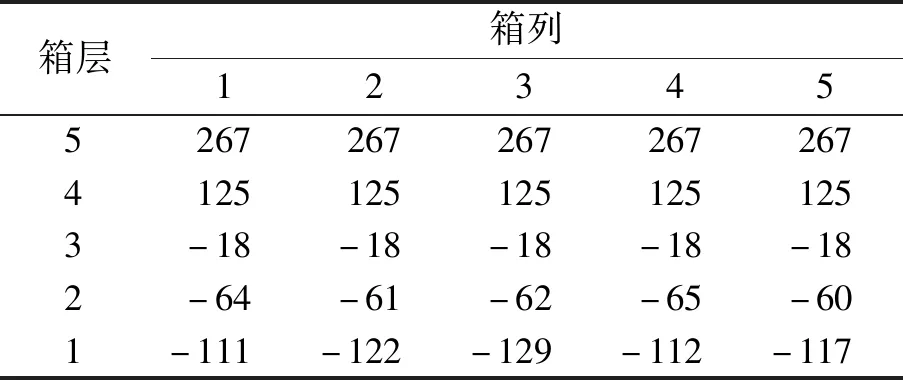
表1 單個集裝箱側傾力矩Mi kN·m
根據式(4)計算得T≥4 484 kN。在實際計算過程中按前述Mi的取值規則取為0。
該船采用的綁扎鋼絲繩直徑為15 mm,其破斷負荷為127~160 kN(具體取決于鋼絲繩結構和抗拉強度,這些參數現已無法確定),遠小于實際承受的拉力4 484 kN,因此必然會崩斷。
3 改進措施
為防止綁繩崩斷導致集裝箱落水,總體上可以從兩方面著手:①降低綁繩承受的負荷(拉力);②提高綁繩本身的許用負荷。具體可采取如下4種措施。
3.1 綁扎方式優化
分析圖3所示的力學模型和式(4)可見,綁繩拉力T與綁繩夾角α關系非常大,當α=90°時T為無窮大,而當α=0°時T達到極小值。因此,可以通過優化綁扎方式,盡可能降低綁繩夾角α,從而降低綁繩拉力T。具體做法為:將綁繩的八字形綁扎方式修改為端面交叉綁扎,見圖5a)。對于存在空缺箱位的情況,需特別對待,見圖5b)和圖5c)。
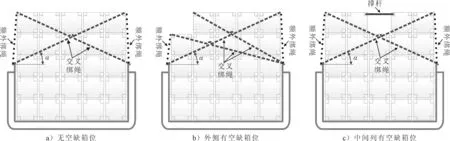
圖5 改進后的綁扎系固方式
此外,考慮到內河集裝箱船積載時集裝箱行與行的間距非常小,由于操作空間不足等原因,手動扭鎖通常難以實施鎖閉操作,集裝箱列的層與層之間垂向連接有效性難以保證。因此,在最外側布置額外的垂向綁繩(見圖5),主要用于確保最外側集裝箱列的層與層之間不會分離。
假設本船采用了改進后的綁扎方式,則對于前面分析的集裝箱堆垛,綁繩夾角α將從87.5°降低到31.6°,綁繩拉力T將從4 484 kN降低到230 kN,降低幅度超過94.8%。
3.2 駕駛行為優化
再次分析式(4)、(2)和(3)可知:當減少船舶橫傾角θ0、降低航速Vm、增大轉彎半徑R,也能降低綁繩拉力T。3個參數中,控制轉彎時的船舶橫傾角θ0最為有效。以前面分析的集裝箱堆垛為例,若能將橫傾角θ0從12.3°降至8°(根據前文橫傾角測算方法,船舶主甲板入水時對應橫傾角為8.6°),則T將從4 484 kN降低到1 716 kN,若同時采用改進后的交叉綁扎,則T將能降低到88 kN,降低幅度超過98%。
因此,可以考慮在船舶出港前,針對當時的積載狀態和綁扎方式,先計算確定一個轉彎時的最大允許橫傾角θ0max,具體做法為:以全速回航為假想狀態(航速和回轉半徑R已知),將綁繩(鋼絲繩)的許用負荷作為其最大允許拉力Tmax,然后通過取不同的橫傾角θ0代入式(2)、(3)和(4)進行迭代計算,使得綁繩計算拉力T盡可能接近但不大于Tmax,此時所得橫傾角即為轉彎時的最大允許橫傾角θ0max,若該值大于主甲板入水時的橫傾角則取甲板入水橫傾角。
船舶航行過程中,駕駛人員需將計算確定的最大允許橫傾角θ0max作為彎道航行時船舶橫傾角的最大限值,并實時優化駕駛行為(如調整舵角和主機轉速等),使船舶實際橫傾角不超過該限值,以此確保綁繩不致于承受過大的拉力而崩斷。
3.3 積載布置優化
進一步分析式(4)和(2)可知,同樣質量的集裝箱,當其位于上層時hi較大,傾側力矩Mi較大,這意味著需要綁繩提供的拉力更大。因此,集裝箱在積載布置時,應盡可能將重箱放在下層,即應符合“下重上輕”的基本原則,此舉也是降低綁繩拉力的重要措施。
分析圖2中各集裝箱的質量分布,發現重箱大多分布在上層,這也是導致綁繩崩斷的一個重要因素。若依次采取上述降低綁繩拉力的改進措施,即先將八字綁扎改為端面交叉綁扎,再限制轉彎時船舶橫傾角不大于8°,最后按“下重上輕”的原則調整集裝箱積載布置,則綁繩拉力T可從4 484 kN降至34 kN,降幅超過99.2%。
3.4 綁繩強化
即選用直徑更大和強度更高的綁繩,此舉旨在提高綁繩的許用負荷。許用負荷一般以安全工作負荷表達,取值等于最小破斷負荷除以安全系數(船舶規范中一般取3)。因此,所選用的綁扎鋼絲繩,其最小破斷負荷應至少大于3倍的綁繩拉力T。
對于前面分析的集裝箱堆垛,在綜合采取綁扎方式優化、駕駛行為優化和積載布置優化措施之后,其綁繩拉力降至34 kN,則選取的鋼絲繩的最小破斷負荷應不小于108 kN。
根據鋼絲繩標準[6-7]選用直徑18 mm、抗拉強度1 870 MPa、結構6×7+FC的纖維芯鋼絲繩(因其柔韌性優于鋼芯鋼絲繩而更受歡迎),其最小破斷負荷為201 kN(鋼芯鋼絲繩為218 kN),是需求的最小破斷負荷的1.86倍,是綁繩拉力的5.58倍,足以避免在彎道航行時崩斷。
4 結論
1)改進綁扎方式,將八字形綁扎修改為端面交叉綁扎,并在最外側布置額外的垂向綁繩以防層間分離,以此降低綁繩所需承受的拉力;對于最外側和中間列存在空缺箱位的特殊情況,也給出了對應的解決方案;
2)優化駕駛行為,出港前根據積載狀態和綁扎方式,計算確定船舶轉彎允許的最大橫傾角,并通過調整舵角和主機轉速確保轉彎時實船橫傾角不超過該限值,以此降低綁繩所需承受的拉力;
3)優化積載布置,確保其符合“下重上輕”的基本原則,以此降低綁繩所需承受的拉力;
4)強化綁繩,選用直徑更大和強度更高的鋼絲繩,以提高綁繩的許用負荷。
綜合采取上述4項改進措施,將可使綁繩所需承受的拉力小于其許用負荷,從而有效防止綁繩崩斷所導致的集裝箱落水。
更智能的解決方案是:船舶積載前獲取準確箱重,利用船載裝載儀計算確定配載與綁扎系固方案,以及彎道航行等各種狀態下的船舶限制橫傾角;實船航行時實時比對船載數字化傾角儀對應的橫傾角,并在分析研判船舶運動狀態后向駕駛人員告警;甚至可以通過智能技術應用為駕駛人員推薦最佳的舵角、主機轉速等,最終實現在限制船舶橫傾角條件下的船舶自主航行。
由于事發時風平浪靜,所以沒有計及風浪造成的船舶運動影響,在實船設計與營運中尚應對這一因素進行考量。

