真空斷路器分斷金屬液橋形成的數值模擬

趙永秀，王 瑤，王 騎，田江暉

(西安科技大學 電氣與控制工程學院，陜西 西安 710054)

0 引 言

真空斷路器分斷產生的電弧會影響斷路器的可靠性及壽命[1-4]。金屬液態橋作為電弧形成的重要階段，決定了建弧時極間金屬蒸氣的含量和陰極斑點的形狀及大小[5-8]，直接影響了電弧是否形成。故研究高壓真空斷路器分斷金屬液橋的形成對探究真空金屬蒸氣電弧產生機理及提高斷路器可靠性具有重要意義。

真空斷路器發生分斷時，電極表面由于熱效應發生熔化在極間形成金屬液橋，進而斷裂產生電弧[9-11]，電極的熱效應伴隨著電弧發展的整個過程。但目前對電極熱過程的研究主要集中在建弧后電極表面的加熱及熔蝕。如通過在大功率條件下探究動靜觸點分斷過程電弧使觸點表面發生的侵蝕現象，分析了觸點分斷速度及橫向和縱向磁場對觸點侵蝕量的影響[12-13]。文獻[14]通過建立大電流真空電弧燃弧過程中的傳熱模型，得出了真空大電流電弧對陽極表面的變形及溫度分布的影響。文獻[15]提出了針對銅鉻合金觸頭熔化過程的計算方法，并得出了對于小電流擴散態電弧和大電流聚集態真空電弧的2種弧后陽極溫度衰減模式。利用高速攝像機拍攝燃弧過程，探究了開斷次數對觸頭腐蝕行為的影響[16-17]。文獻[18]比較分析了觸頭材料在焦耳熱和電弧作用下的響應過程，指出在液橋斷裂時觸頭溫度的變化由焦耳熱作用逐漸轉為電弧作用。上述研究雖解釋了弧前觸頭溫度變化的原因，但并未對弧前的熱行為進行具體研究。

目前對弧前電極熱過程的研究主要針對金屬液橋斷裂前的溫度分布及電流對其變化的影響，且不同電極材料分斷時其溫度變化的規律也不相同。對于以AgNi10為材料的觸頭，從分離到熔融金屬液橋的產生，其中心節點溫度與分離時間呈指數變化關系[19]。文獻[20]通過建立不同電極材料的電接觸模型，分析了熱導率對Ag、AgPd60、Pd這3種組合電接觸材料分斷時金屬液橋斷裂的影響。而對于真空斷路器常用的銅觸頭材料的研究，文獻[21]探究了金屬液橋斷裂前的溫度及電流密度分布，但僅從溫度角度判斷金屬液橋是否發生熔化，并未給出實際的熔化相變過程。文獻[22]探究了真空環境下銅觸頭分斷初始電流對金屬液橋形成的影響，但未考慮電極表面微觀形貌等其它因素產生的影響。

為研究高壓斷路器觸點分斷金屬液橋的形成，考慮金屬液橋形變，建立真空環境下銅觸點電接觸模型；得出金屬液橋形成的相變變化、電勢及溫度分布；進而探究觸點分斷初始電流、表面粗糙高度及觸點初始接觸壓力對金屬液橋的影響。為深入研究真空金屬蒸氣電弧形成機理及提高斷路器可靠性奠定理論基礎。

1 真空斷路器觸點電接觸模型

為研究高壓真空斷路器觸點分斷時金屬液橋的形成，需建立有關金屬液橋的幾何模型及數學模型，對其做如下假設。

1)忽略環境中磁場的影響，則熱傳遞方式僅考慮熱傳導和熱對流，不考慮熱輻射作用。

2)僅考慮電極接觸面的收縮電阻，忽略膜電阻的影響。

3)假設金屬液橋形成過程中電流恒定，即為一個無源場，故?q/?t=0。

1.1 幾何模型

由于真空斷路器分斷時建弧階段為微秒尺度微米量級，金屬液橋的形成過程極短，因此可采用固定間距來模擬斷路器分斷時金屬液橋形成的瞬態過程。在模型建立時，將觸點實際接觸區域處理為機械接觸斑點(簡稱為接觸斑點)，金屬液橋存在原區域處理為導電斑點(a斑)。由文獻[23]可知，一個機械斑點通常由一個或多個a斑組成，銅電極材料上的接觸斑點直徑約為100 μm，a斑直徑約為10 μm。因此，建立斷路器觸點電接觸幾何模型如圖1所示。

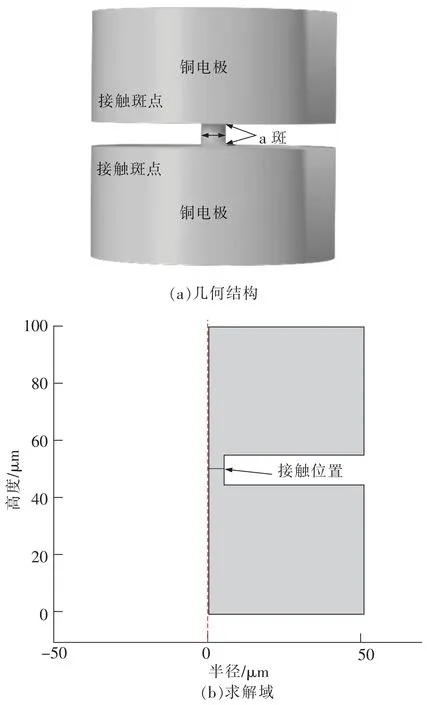
圖1 真空斷路器觸點電接觸幾何模型Fig.1 Electric contact geometry model for vacuum circuit breaker contacts

1.2 數學模型

真空斷路器觸點分斷瞬間金屬液橋的形成伴隨著復雜的熱-電耦合效應，液橋的溫度及形變變化對電弧的形成具有重要影響作用。為探究金屬液橋的溫度分布，考慮了熱傳導、熱對流、焦耳熱及熔化相變過程中材料屬性變化的影響。同時計算了由溫度變化產生的熱膨脹力及表面張力對液橋形變的作用。

通過能量守恒方程可得電接觸模型的溫度控制方程為

(1)

式中ρ為密度；Cp為恒壓熱容；t為時間；T為溫度；k為導熱系數；u為流體的速度場；Q為熱源。

由(1)式可知，為探究電接觸模型溫度隨時間的變化，除了需分析熱量的來源，還需求解相變材料的物理屬性密度、恒壓熱容和導熱系數以及銅觸點熔化后的速度場。

電極表面熱量主要來自電流通過導體產生的焦耳熱，結合歐姆定律微分形式對焦耳定律的微分形式進行變換，可得電流產生的焦耳熱量為

(2)

式中Qe為電磁熱，即焦耳熱;J為電流密度；σ為電導率。

將(2)式代入(1)式，可得熱-電耦合后的溫度控制方程為

(3)

由(2)式可知，為得出電接觸模型中的焦耳熱變化量，需對模型中的電流密度J進行求解。因此假定該模型的物理場為無源場，由恒定電流連續性方程得出電場的控制方程為

·J=0

(4)

J=σE

(5)

E=-U

(6)

式中E為電場強度；U為電勢梯度。

隨著焦耳熱量的增加，電接觸模型溫度不斷升高，當溫度上升到銅材料熔點Tm=1 357 K附近時，觸點開始發生熔化相變，此時液態銅的體積分數迅速從0變為1，其溫度轉變區間為2 K，熔化潛熱Lm為208 667.7 J/kg，其熔化相變過程可用如圖2的近似階躍曲線表示[24]。

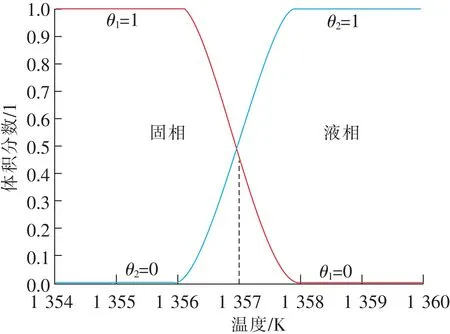
圖2 銅的熔化相變體積分數隨溫度的變化Fig.2 Variation of melting phase change volume fraction of copper with temperature

由圖2可見，銅電極的熔化過程可表示為

θ1+θ2=1

(7)

式中θ1為固相銅的體積分數；θ2為液相銅的體積分數。

結合圖2的熔化相變曲線，利用顯熱容法分別對銅觸點發生熔化相變時其密度、恒壓熱容及熱導率參數的變化進行如下近似處理，可表示為

ρ=θ1ρ1+θ2ρ2

(8)

(9)

k=θ1k1+θ2k2

(10)

式中ρ1,ρ2分別為固態和液態銅的密度；Cp，1，Cp，2分別為固態和液態銅的恒壓熱容；k1，k2分別為固態和液態銅的導熱系數；αm為銅的相變質量分數。

當金屬液橋原區域發生熔化后，液態銅區域產生速度場。考慮壓力及粘性力的作用，通過動量守恒方程與連續性方程描述不可壓縮流體液態銅的流動，進而可得出速度場的變化。其中動量守恒方程為

(11)

式中p為流體微元上的壓力；I為單位矩陣；μ為動力粘度。

連續性方程為

ρ·(u)=0

(12)

為探究金屬液橋形成過程中發生的形變，考慮了銅觸點電接觸模型隨溫度升高受到的熱膨脹作用以及熔融邊界受到的表面張力作用。

僅考慮熱應變影響，則熱膨脹作用使模型表面產生的位移變化可表示為[25]

(13)

式中x為位移場；C為四階彈性張量；E為楊氏模量；v為泊松比，“∶”為雙收縮；εth為熱應變。

其中，熱應變為

εth=α(T)(T-Tref)

(14)

式中α(T)為熱膨脹系數；Tref為參考溫度，取293.15 K。

通過熱誘導引起的馬蘭格尼效應將壓力和粘性力的法向分量與溫度的切向導數相關聯，可得熔融邊界受到的表面張力為

[-pI+μ(u+(u)T)]n=γtT

(15)

式中，γ為表面張力溫度導數。

文中考慮銅觸點發生熔化相變時的材料屬性變化，通過共同耦合求解傳熱方程、電場方程和N-S方程，模擬真空斷路器觸點電接觸模型的熔化相變過程，同時考慮了液橋形變受溫度變化引起的熱膨脹作用及馬蘭格尼效應的影響。

2 金屬液橋仿真結果分析

基于上述建立的真空環境下銅觸點電接觸模型，通過COMSOL有限元多物理場軟件耦合電流、多孔介質傳熱、層流及固體力學模塊，數值計算真空斷路器在分斷初始電流為100 A時的金屬液橋電勢及溫度分布，并分析金屬液橋形成過程中的相變變化。

2.1 金屬液橋電勢分布

通過數值模擬金屬液橋的形成過程，得出金屬液橋的電勢分布如圖3所示。

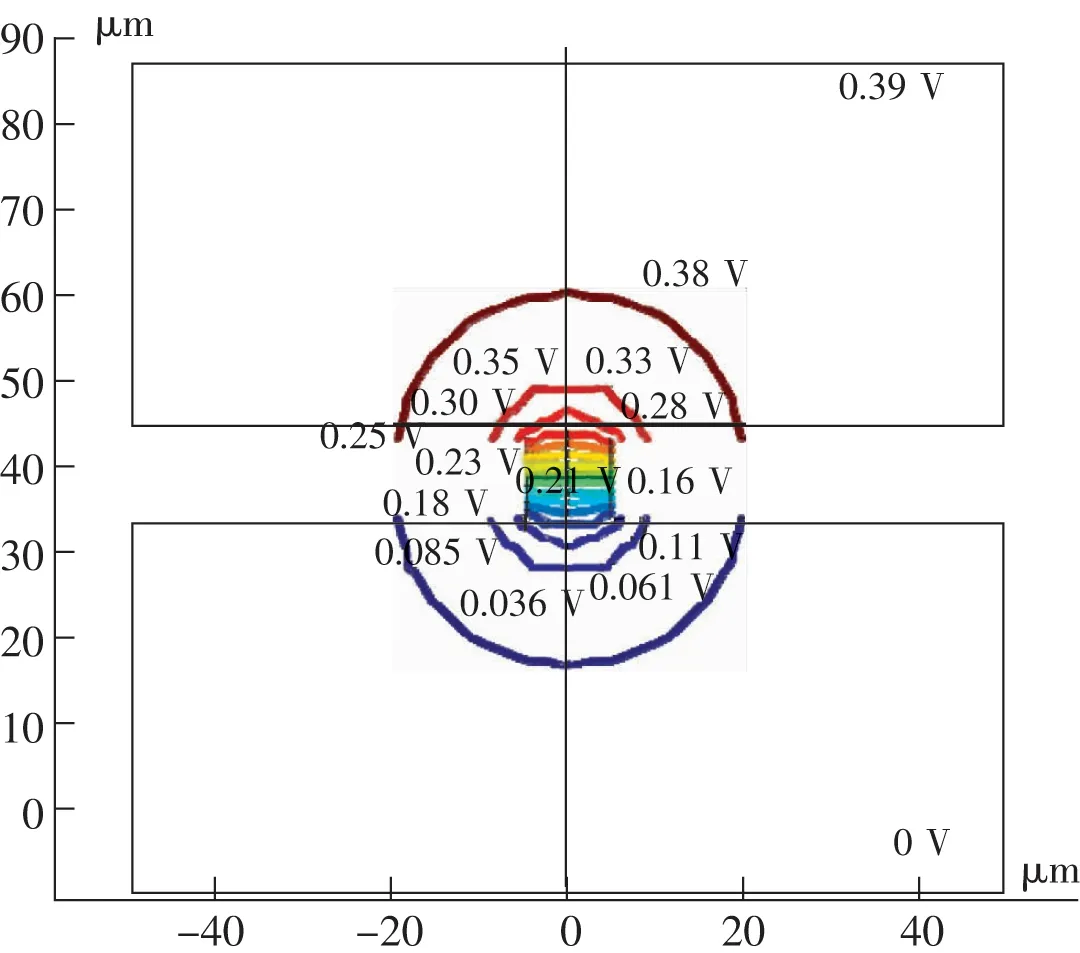
圖3 金屬液橋的電勢分布Fig.3 Electric potential distribution of metal bridge

由圖3可見，金屬液橋的電勢差由電接觸位置向電極兩邊逐漸減小，這是由于原金屬液橋區域相對機械接觸斑點面積減小，因此當相同電流流過時，原金屬液橋區域電流密度更大，從而造成此處電勢差較大。同時發現金屬液橋的熔化電壓為0.39 V，與文獻[26]中銅材料的熔化電壓相比略低，這是由于在本模型中未考慮膜電阻的影響作用。

2.2 金屬液橋溫度分布及相變

考慮由溫度變化引起的熱膨脹作用及不同流體之間的表面張力作用，在焦耳熱作用下，銅觸點分斷形成金屬液橋的溫度分布及相變變化如圖4所示。

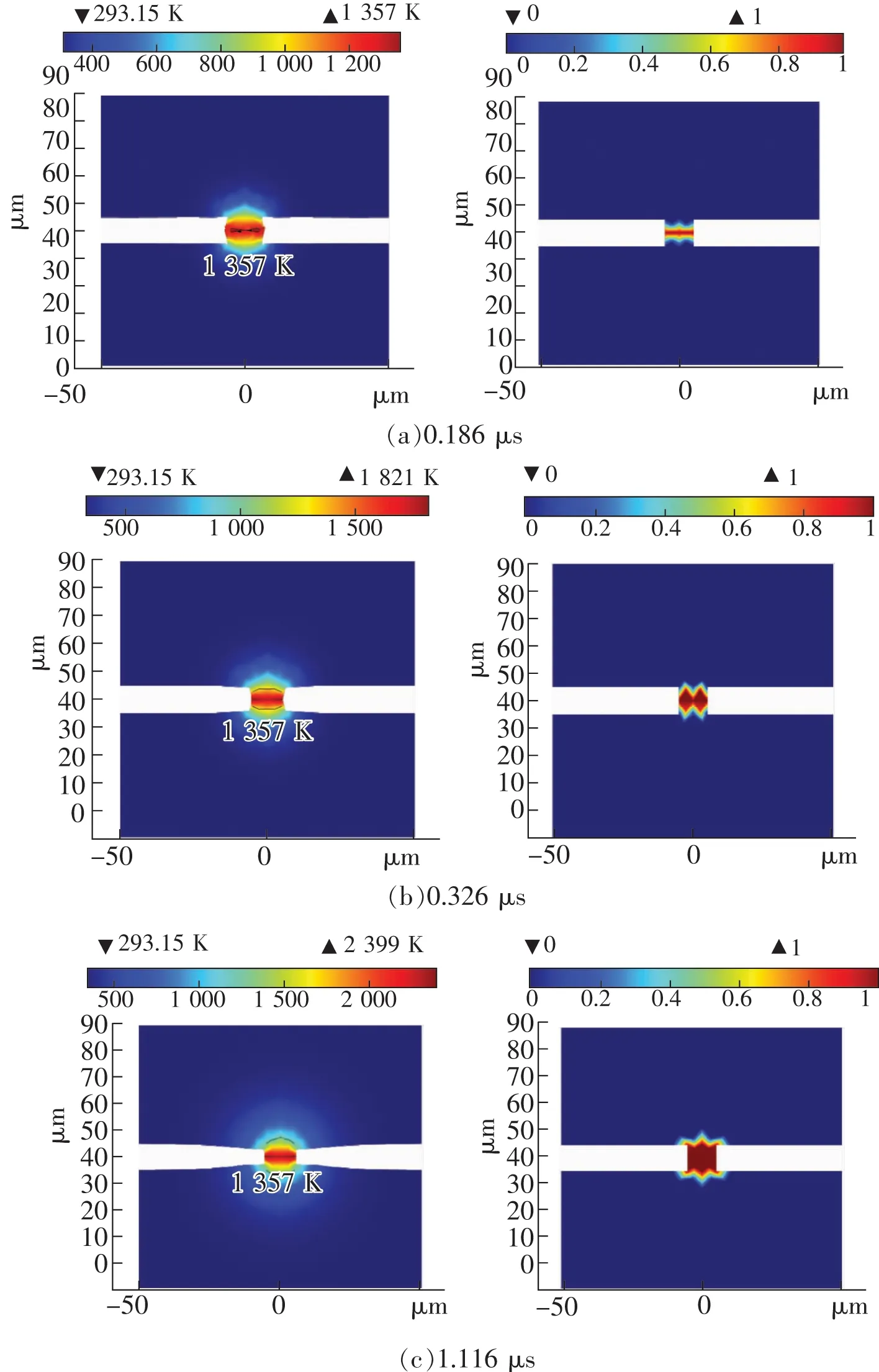
圖4 金屬液橋形成過程中的溫度分布及相變變化Fig.4 Temperature distribution and phase transition changes during the formation of metal bridge

由圖4可見，真空斷路器觸點電接觸模型在t=0.186 μs時，電接觸位置溫度最先開始發生熔化相變，a斑區域受熱膨脹力與表面張力共同作用，此時熱膨脹力大于表面張力作用，因此a斑區域體積相應增大；當t=0.326 μs時，發生熔化相變的區域增大，此時表面張力作用大于熱膨脹作用，a斑區域開始向內收縮；隨著溫度的繼續升高，在t=1.116 μs時，a斑區域全部發生熔化，此時金屬液橋在熱膨脹力與表面張力的共同作用下變形最為顯著，由最初的圓柱形變為啞鈴型。

由上述分析可知，金屬液橋的最高溫度最先出現在電接觸位置，這是由于電流從面積較大的接觸斑點流入面積較小的a斑點區域時，電流密度增加，焦耳熱作用增強。此外，金屬液橋發生形變主要受熱膨脹力與表面張力的共同影響。

3 金屬液橋影響因素

金屬液橋形成的主要影響因素有電路參數、電極表面微觀形貌及電極材料性質等。為分析分斷初始電流、觸點初始接觸壓力及表面粗糙高度對金屬液橋形成的影響規律，分別數值求解了電流為100，120，140和160 A，觸點間初始接觸壓力為8×108，6×109，1.12×1010和1.64×1010Pa，觸點表面粗糙高度為0.1，0.2，0.3和0.4 μm時金屬液橋熔化所需時間，其變化規律如圖5所示。

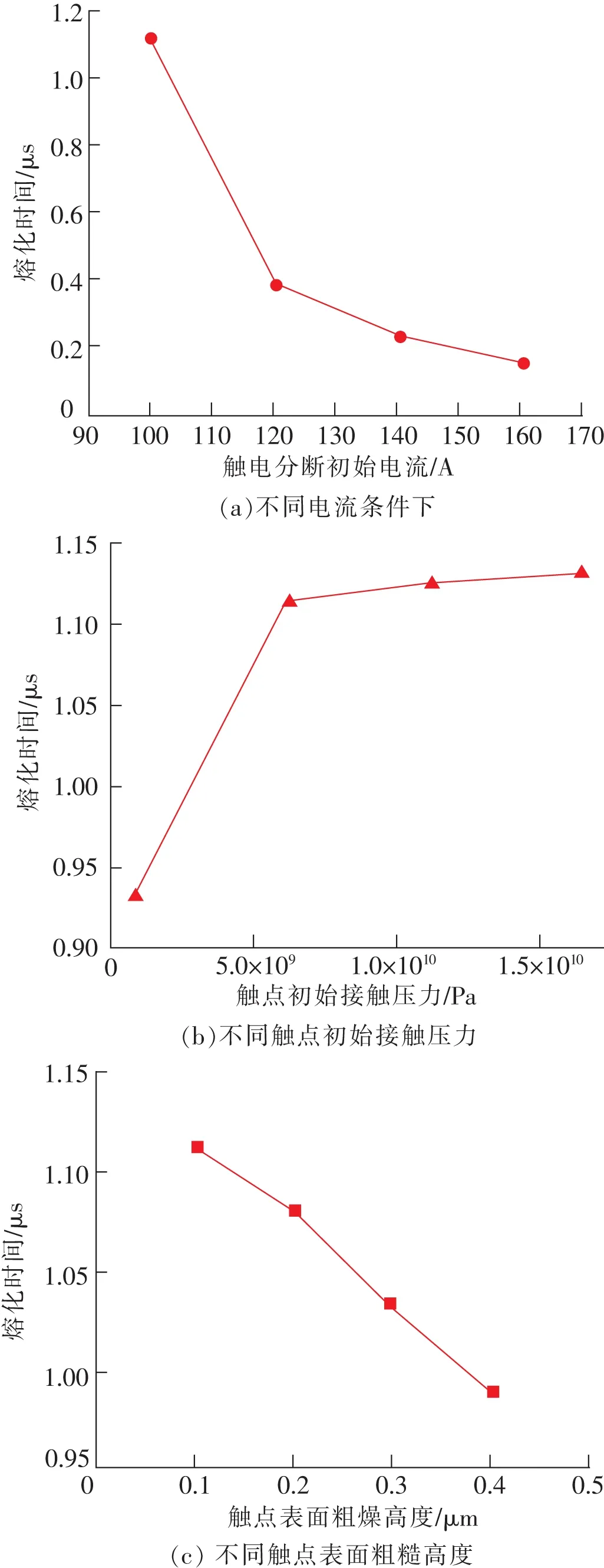
圖5 不同條件下金屬液橋熔化所需時間Fig.5 Melting time of metal bridge under different conditions

由圖5可知，金屬液橋熔化所需時間隨著觸點初始接觸壓力的增大而增大，隨著電流和觸點表面粗糙高度的增大而減小。金屬液橋的形成是電弧產生前的必經階段，電流和觸點表面粗糙高度越大或觸點間初始接觸壓力越小，熔化的電極材料就越多，由此可推斷，金屬液橋的形成直接決定其斷裂后極間金屬蒸氣的含量和蒸氣壓；同時金屬液橋的形變將會影響弧前電極的微觀表面形貌，而極間金屬蒸氣含量及電極表面的微觀形貌對極間氣體擊穿和電弧能否形成具有決定性作用。因此，對金屬液橋形成及其影響因素的研究對提高斷路器的可靠性具有重要意義。

4 結 論

1)通過金屬液橋形成時的電勢分布，得出其電勢差由電接觸位置向電極兩邊逐漸減小；銅觸點分斷金屬液橋的熔化電壓與銅材料的熔化電壓近似相等，證明仿真模型的正確性。

2)金屬液橋的最高溫度出現在電接觸位置；其形變受熱膨脹力與表面張力共同影響，但隨著熔化相變體積逐漸增大，金屬液橋變形的主導因素由熱膨脹力逐漸轉換為表面張力作用，因此從最初的圓柱形變為啞鈴型。

3)分斷初始電流或觸點表面粗糙高度越大，金屬液橋形成時間越短；而觸點間初始接觸壓力越大，金屬液橋熔化所需時間越長。