基于改進的分段常數自適應動態逆控制方法研究

李煜, 劉小雄, 何啟志, 章衛國, 黃天鵬

(1.西北工業大學 自動化學院, 陜西 西安 710129; 2.陜西省飛行控制與仿真技術重點實驗室, 陜西 西安 710129;3.中國航空工業集團公司西安飛行自動控制研究所, 陜西 西安 710076)

如何提高航空器安全性和可靠性一直是熱點問題。在飛行過程中，各種不確定因素的存在都會對飛機的飛行性能產生影響。例如，戰斗機發射導彈以及運輸機低空空投都會改變飛機重心位置，而重心位置與飛機的動態性能和穩定性有著密切的關系，重心的變化會降低控制性能，甚至破壞飛機自身的穩定性。此外，執行機構故障嚴重威脅著飛機安全飛行以及飛行員的生命安全。因此，通過提高飛行控制系統的魯棒性，使其在飛行中主動或者被動克服所遇到干擾，對飛機安全飛行具有深遠的意義。

1992年，學者Snell等[1]首次將非線性動態逆控制方法(nonlinear dynamic inversion,NDI)應用到戰斗機控制律設計中，出色地展現出NDI方法快速性好以及解耦能力強的特點。由于NDI控制方法的特點契合了現代戰機對性能的要求，因而該方法一經提出，就得到了國內外學者的廣泛關注。

由于各類因素的制約和限制，實際工程中難以獲取精確的氣動數據，導致NDI控制器無法精確消除飛機中非線性部分，進而降低了控制性能。針對NDI暴露出魯棒性不足的問題，眾多學者對該方法進行改進，旨在保留其優秀特性的同時，降低NDI方法對精確模型的依賴，達到提高NDI控制器的魯棒性的目的。根據國內外學者發表的文章來看，對NDI控制的改進方式主要集中在增量NDI(incremental NDI，INDI)[2-3]和自適應NDI(adaptive NDI，ANDI)[4-6]兩方面。INDI控制方法采用泰勒級數展開的方式對模型進行簡化，得到控制輸入增量與狀態量之間的關系，進而采用NDI控制“反演求逆”的方法推導出INDI控制律。由于INDI控制律中采用角加速度信號來替代原本NDI中與非線性模型相關的信息，因而INDI控制律在降低對模型的依賴的同時提高了系統對擾動的魯棒性[7]。引入角加速度信號是INDI的精髓，但是實際中沒有相應的傳感器去直接測量角加速度信號，并且通常采用對角速度信號差分濾波的方式來獲取角加速度。由于這一過程很難保證實時性，并且得到的角加速度信號中的誤差還會直接降低到INDI的魯棒性[8]。因此，這對INDI方法的實際應用造成了一個嚴峻的挑戰。

自適應控制則是在控制器中加入自適應結構，根據動態誤差估計出模型不確定性以及擾動對系統產生的影響，在控制器中予以補償，達到提高控制器魯棒性的目的。目前對自適應控制理論和應用的研究較為成熟，典型的自適應算法都包括神經網絡自適應[9]、L1自適應[10]等。因此將NDI控制與自適應控制結合，提出自適應動態逆控制方法來增強NDI控制器的魯棒性。相比于INDI，ANDI不需要引入額外的角加速度信號，并且ANDI控制方法保留NDI控制優良的動態特性和解耦能力的同時，兼顧了自適應控制的魯棒性，使得基于此方法設計的控制器能夠克服飛行過程中擾動對飛機的影響。文獻[4]針對高超聲速飛機提出一種自適應動態逆控制增強控制系統的魯棒性，克服了高速條件下的強耦合性和強非線性對飛機的影響，最終實現了所期望的跟蹤性能。文獻[5]針對艦載機著艦問題，提出一種基于改進的神經網絡自適應動態逆控制方法，并基于此方法設計艦載機縱向控制律，用于消除艦尾流對艦載機影響。由于該方法引入自適應學習率來加快神經網絡的收斂速度，進而保證控制器的魯棒性，提高了著艦精度。文獻[6]同樣將神經網絡和動態逆方法結合，根據最優控制理論設計神經網絡權值的自適應律。在飛機發生舵面故障時，神經網絡權值進行調整，重構出舵面故障所導致的誤差，并由控制器進行補償，從仿真結果來看該方法達到預期的控制效果，保證舵機故障下飛機的操縱品質。

以自適應控制為線索，為了解決動態逆方法對參數擾度敏感的問題，本文提出一種基于分段常數的自適應動態逆控制策略，并對分段常數自適應算法[11]進行改進，旨在減小CPU運行負擔的同時提高該算法對擾動影響估計的精度。此外，基于改進的分段常數自適應動態逆控制設計先進戰斗機控制律。仿真結果表明，本文所設計的控制器能夠增強控制系統的魯棒性，針對重心突變干擾和執行機構故障，該控制器能夠有效克服以上擾動的影響，對于飛機的安全飛行具有一定的工程應用價值。

1 自適應動態逆控制方法

自適應動態逆控制器由動態逆控制器、參考模型和自適應律三部分組成。其中參考模型提供期望的系統動態性能；自適應律和控制律則根據系統與參考模型之間的響應誤差對擾動進行估計和補償，促使被控對象達到滿意的動態性能。本節主要對干擾影響下的模型進行分析，并且設計相應的控制律、參考模型和自適應律。

1.1 干擾影響下的模型分析

通常情況，擾動下的系統微分方程可表述為：

(1)

式中:x(t)∈Rn×1是系統狀態;f(x)∈Rn×1表示與控制無關的系統非線性光滑向量函數;G(x)∈Rn×m(n≤m)表示與控制相關的系統控制效能矩陣;u(t)∈Rm×1是系統的控制輸入;C∈Rm×n為系統輸出矩陣;而y(t)∈Rm×1表示系統的輸出。特別的,λ(t)∈Rm×m表示輸入增益對角矩陣;δ(x,t)∈Rn×1表示系統受到的擾動,包括模型不確定性、外部擾動等。系統滿足以下幾個假設:

假設1系統控制效能矩陣的逆(偽逆)存在。即G(x)-1G(x)=I或G(x)+G(x)=I。

假設2擾動δ(x,t)全局有界。即存在常數D>0和X>0,使得擾動在任意時刻t>0,且狀態量有界‖x‖∞≤X的范圍內滿足‖δ(x,t)‖∞≤D。

假設3擾動δ(x,t)偏導數存在且有界。存在常數dδ,t>0和dδ,t>0,則擾動偏導數滿足

(2)

假設4輸入增益矩陣λ(t)是符號已知的非奇異對角矩陣,其對角線元素λii(i=1,2…n)滿足0≤λii≤1。理想情況下為單位陣;如果部分控制面性能降級,則對應元素λii∈(0,1);如果完全失效則對應元素λii為零。

由于控制器需要克服干擾影響,因此類比參考文獻[10],將系統(1)其變換成以下形式

(3)

式中,σ(x,t)和δ(x,t)滿足δ(x,t)=G(x)σ(x,t)。

1.2 自適應動態逆控制器設計

采用反饋求逆的思想設計動態逆控制律,動態逆控制律如下

(4)

vd(t)=Kω(xcmd(t)-x(t))

(5)

式中:Kω為對角增益陣,滿足Kω,ii>0,i=1,2…n;xcmd為系統的輸入指令。

1.3 參考模型設計

參考模型的功能是為系統響應提供的參考。其功能決定了參考模型具有系統期望的動態。因此參考模型的響應是被控對象理想的響應。考慮到自適應動態逆控制律(4)形式,系統參考模型可設計為

(6)

(7)

1.4 基于改進的分段常數的自適應律

分段常數自適應算法是一種典型的自適應律的設計方法。該算法有以下幾個不可替代的優勢:a)該算法結構簡單、計算量小,不會給系統帶來額外負擔;b)能夠保證系統信號的半全局一致界性;c)在保證系統穩態性的同時兼顧了系統的瞬態性能。

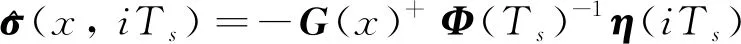
(8)

式中,Φ(Ts)和η(iTs)具體如下

Φ(Ts)=-K-1(e-KTs-In)

(9)

(10)

在自適應律中,Ts為系統采樣時間間隔;In為n階單位陣;Kσ表示增強因子的對角矩陣,其作用是提高系統穩態精度。特別的,對角線元素滿足

Kσ,ii∈(0,1), (i=1,2…n)

2 控制系統性能分析

在對自適應動態逆控制性能分析之前,定義在分析過程中用到的一些參數。

定義ζ(Ts)κ(Ts)Δ為由控制輸入和干擾引起的狀態輸出的上界,其中κ(Ts)與Δ的定義如下

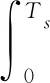
(11)

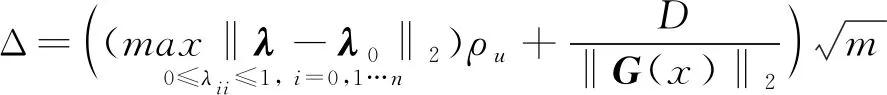
(12)

α1(t),α2(t),α3(t)的定義具體如下

(13)

在采樣周期Ts內α1(t),α2(t),α3(t)的最大值可以表示為

(14)

2.1 穩定性分析

(6)式與(3)式相減能夠得到誤差動態

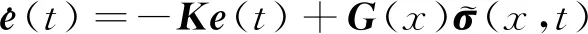
(15)

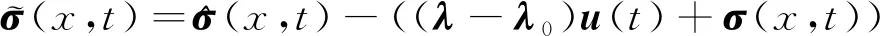
(16)

在iTs+t時刻下,系統的誤差動態方程的解為

(17)

定義狀態量在iTs時刻狀態誤差引起的解

(18)

同樣,定義干擾項在iTs時刻引起的解

(19)

在時間間隔[jTs, (j+1)Ts]內,且(j+1)Ts<τ,則(j+1)Ts時刻下系統的預測誤差為

e((j+1)Ts)=ζ1((j+1)Ts)+ζ2((j+1)Ts)

(20)

式中

在改進后的分段常數自適應律(8)～(10)式作用下ζ1((j+1)Ts)變為

ζ1((j+1)Ts)=-Kσe((j+1)Ts)

(23)

將(23)式代入到預測誤差方程(20)式中,可進一步變型為

e((j+1)Ts)=(I+Kσ)-1ζ2((j+1)Ts)

(24)

由于干擾的滿足假設2,并且根據(11)式和(12)式對κ(Ts)和Δ的定義,可得

(25)

(25)式得到的上界對所有(j+1)Ts≤τ都成立,因此對于iTs≤τ,(26)式同樣成立。

‖e(iTs)‖2≤‖(I+Kσ)-1‖2ζ(Ts), ?iTs≤τ

(26)

在所有iTs+t≤τ,t∈(0,Ts]的范圍內,根據式(13)對α1(t),α2(t),α3(t)和Δ的定義,誤差的二范數如下

(27)

將(26)式帶入(27)式,可變形為

(28)

將右側定義為γ0(Ts),見(29)式。

(29)

根據(13)式和(14)式的定義不難推出

(30)

所以,當時間間隔Ts很小時,誤差的極限為

(31)

因此對于任意t∈[0,τ],都有

(32)

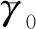
1) 擾動影響下,基于改進的分段常數自適應律((8)～(10)式)在時間間隔Ts能夠保證系統的穩定性。因此在整個控制過程,系統的全局穩定和瞬態性能都得到了保證。

2) 通過提高頻率來減小時間間隔Ts能夠有效降低誤差的范圍,進而提高系統響應穩態精度,但與此同時會增加CPU的負擔。

3) 由于‖(I+Kσ)-1‖2<1,因此增強因子Kσ的加入縮小了誤差的收斂性范圍。改進后的分段常數自適應能夠在不減小時間間隔Ts的條件下提高估計精度,進而達到減小系統的誤差的目的,避免了增加頻率對CPU造成過重負擔。

2.2 動態特性分析

當采樣間隔Ts很小時,可以忽略系統狀態誤差。此時為了分析系統的動態特性,引入非自適應形式的閉環動態系統,如(33)式所示

(33)

此時,結合(5)式,閉環系統響應為

(34)

3 自適應動態逆角速度控制律設計

3.1 模型描述

前緣襟翼的控制指令由迎角α、靜壓ps和動壓Q根據控制函數自動生成,控制律如下

(35)

通常情況下,戰斗機的角速度運動方程可寫為

(36)

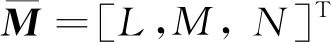
Cnδa,lCnδr為各控制面的操縱導數。

戰斗機側滑角運動方程可描述為

(39)

式中:g為重力加速度;Va表示真空速;φ和θ分別表示滾轉角和俯仰角。

3.2 角速度控制策略及控制器設計

對于縱軸和側軸,飛行員的桿指令分別直接對應飛機的俯仰和滾轉運動。飛行過程中由于不希望側滑角產生,因此在方向軸上腳蹬對應側滑角指令而不再是偏航角速度,以便保證飛機的側滑角為0。

角速度控制律的性能直接影響到飛機的操縱品質。品質優秀的角速度控制律要保證在各種不確定擾動下飛機的角速度都能跟蹤上駕駛員的指令,因此采用基于改進后的分段常數自適應動態逆控制方法來提高角速度控制律的魯棒性。自適應動態逆控制律設計為

(40)

參考模型設計為

(41)

基于改進后的分段常數自適應律為

(42)

式中,Φ(Ts)和η(iTs)如(8)～(10)式所示。

考慮到側滑角響應速度遠遠慢于偏航角速度響應,因此根據奇異攝動理論,在側滑角變化時可認為偏航角速度已經跟蹤上所給指令。因此將側滑角控制器的輸出作為偏航角速度的指令。

由于側滑角與偏航角速率之間的幾何關系相對清晰,因而采用積分式動態逆方法設計側滑角控制律,具體設計如下

(43)

式中,νβ表示側滑角的虛擬控制量,具體如下

(44)

式中,Kβ=2,Kβi=0.25。

綜上,戰斗機角速度控制策略如圖1所示。

圖1 基于自適應動態逆控制的角速度整體控制結構

4 仿真驗證

本節采用matlab/simulink對所改進后的分段常數自適應動態逆控制角速度控制器的魯棒性和動態性能進行驗證和分析。

所有仿真都在6 000 m高度,150 m/s速度的巡航條件下完成。在該巡航條件下飛機的配平狀態為α=θ=3.49°,δe=-4.34°以及油門開度δth=0.25,其余狀態和舵面偏轉為0。

表1 操縱面限制

參考模型以及系統采樣頻率為100 Hz,即時間間隔為Ts=0.01 s。采用一階慣性環節來模擬操縱面的執行機構,對于不同操縱面的幅度與速率限制具體如表1所示。

4.1 操縱面執行機構故障

在常見的“舵面卡死”和“舵效降級”故障干擾下,對所設計控制器的魯棒性進行驗證。同時給戰斗機帶有指令濾波的俯仰角速率和滾轉角速率指令,期間始終保持側滑角為零。

在飛行過程中,假設10 s飛機左升降舵出現故障,故障使得左升降舵舵效降低20%;在15 s時飛機右升降舵卡死在-5°。在24 s和25 s時飛機左、右副翼也分別出現性能降級故障,故障使得舵效降低50%和35%。仿真結果如圖2至8所示。

圖2 執行機構故障下,俯仰角速度響應曲線 圖3 執行機構故障下,滾轉角速度響應曲線 圖4 執行機構故障下,側滑角響應曲線

圖5 左、右升降舵偏轉曲線 圖6 左、右副翼偏轉曲線 圖7 方向舵偏轉曲線

圖8 改進后的分段常數自適應律估計出參數

正常飛行時,俯仰角速度和滾轉角速度能夠快速準確地跟蹤上指令;當執行器出現故障后,分段常數自適應律開始參與調整,因此,飛機能克服擾動影響快速恢復至平衡,并且后續角速度依舊能達到期望的動態性能,整個過程展示出所設計基于改進的分段常數自適應動態逆控制器優秀的魯棒性。

4.2 重心突變干擾

重心位置是飛機的重要參數之一,該變化直接影響到飛機的操縱性和動態性能。本小節則在飛機受擾重心突變情形下對比驗證所設計改進后的分段常數自適應動態逆控制的性能。

同樣,給飛機帶有指令濾波的俯仰角速率和滾轉角速率指令,并且要求側滑角始終為零。在12 s時飛機重心發生突變,假設重心偏移Δx=0.1 m,Δy=0.1 m,Δz=0.1 m。對比改進前、后分段常數自適應算法設計的角速度控制器和常規動態逆控制器控制效果,對比結果如圖9至11所示。

圖9 重心突變下，滾轉角速度響應對比曲線 圖10 重心突變下，俯仰角速度響應對比曲線 圖11 重心突變下，側滑角響應對比曲線

從對比結果能看出：正常飛行時，3種動態逆控制器作用下的角速度響應相同；但在重心突變后，常規動態逆控制器性能存在明顯下降。相反，改進前、后的自適應動態逆控制器能夠克服重心突變造成的影響，保證擾動下角速度的性能，但改進后的分段常數自適應動態逆控制器的準確性更高，表現在角速度的穩態誤差明顯最小。整體上來看，基于改進的分段常數自適應動態逆控制器結果不僅表現出強大的魯棒性，而且突出了準確性高的優點。

5 結 論

本文提出一種基于改進的分段常數自適應動態逆控制方法,用于提高控制系統的魯棒性。仿真結果表明，基于此方法設計角速度控制器在執行機構故障和重心突變干擾下，表現出令人滿意的控制性能。