對地協同觀測混合星座多目標優化設計

賀波勇, 曹靜, 周慶瑞, 王建國

(1.西安衛星測控中心 宇航動力學國家重點實驗室, 陜西 西安 710043; 2.西北工業大學 航天學院, 陜西 西安 710072;3.中國空間技術研究院 錢學森空間技術實驗室, 北京 100094; 4.中國人民解放軍91515部隊, 海口 三亞 572016)

混合星座是指由攜帶功能相似或功能不同的有效載荷，為協同完成某項任務而組合在一起的2個或2個以上子星座構成的復合星座。對地觀測衛星主要有電子偵察衛星、光學成像衛星和合成孔徑雷達(synthesized aperture radar,SAR)成像衛星等類型。電子偵察衛星通過無線電信號定位，幅寬可達2 000～3 500 km，但探測精度較低(約10～30 km)，且只能對目標進行定位。光學成像衛星可分為可見光成像和紅外成像，可見光需要滿足一定的光照要求，而紅外成像可以實現全天時目標探測，空間分辨率高一般在0.1～2 m之間，但使用軌道高度較低，幅寬通常只有30～60 km。SAR最高可實現0.1～0.3 m的探測分辨率，具有全天候成像功能，不足之處與光學成像衛星相同，幅寬只有30～60 km[1]。可見，協同利用多種衛星不同優點，可以實現較高對地觀測效率，獲取高品質信息[2-3]。然而，我國目前對地觀測主要是單星應用或少數幾顆衛星配合應用，難以應對日益增長的對地觀測任務需求[4]。

可以將現有星座設計方法分為3類：①幾何解析法，一般衛星數目較少，不需要星間鏈路，可以通過軌道力學領域知識進行分析設計；②基于仿真計算的比較評估設計法，依靠軌道力學領域知識擬定多種方案，通過計算和比較每種方案的性能指標，人工優選[5-6]；③基于現代優化算法的設計方法，這類方法通常將衛星數目、分布軌道面數目和部分軌道參數一起編碼，采用數千次迭代得到計算結果。該方法用于同構星座設計時設計變量數目大幅減少，便于計算收斂，如遺傳算法[7]、復形調優法[8]等。傳統優化星座時，在滿足基本地面覆蓋指標情況下，一般將星座部署代價(可簡化為衛星數目)作為權值最大的一個優化指標[9]，得到的星座并不實用[10]。實際星座部署代價工程計算模型非常復雜，涉及衛星數目、衛星平臺、載荷、電源系統、能否一箭多星發射、不同運載火箭差價等航天工業品市場價格因素，星座中衛星運行軌道高度又直接影響地面覆蓋性和對地分辨率，這又和觀測載荷的型號選擇相關，又與衛星平臺、電源系統、火箭型號相關[11]。混合星座中不同軌道高度的衛星受攝動影響，構型自然保持時長和構型保持控制所需代價也是混合星座必須考慮的優化設計指標，文獻[12]設計的全連通星間鏈路星座的不足是忽略了構型穩健保持問題。文獻[13]利用大偏心率橢圓凍結軌道和赤道圓軌道組成的異構預警星座避免了構型攝動保持問題，但大橢圓軌道不適合要求穩定分辨率的對地觀測任務。隨著經濟發展和航天產品的商業市場化，衛星制造成本大幅降低，對地觀測數據對國土資源、海洋監視、商業經濟、氣象預報、環境保護、災害監測、軍事支援等方面的支撐作用日益突出，星座對地觀測的時間效率、空間分辨率和遙感信息即拍即傳等功能的優化指標權重需大于星座部署代價指標。

針對以上問題，結合我國現有衛星性能，提出了考慮星間鏈路的對地觀測混合星座多目標優化設計模型，并驗證模型的合理性。

1 問題描述

星座設計是指同時設計多個衛星任務，用以協同完成某一特定任務，一般包括衛星類型、個數、工作軌道，相互協同工作關系以及發射部署和長期構型保持等因素。

1.1 設計目標

星座設計目標主要有對地觀測性能品質和成本兩方面指標，而對地觀測性能品質又可分為全球普查覆蓋率、區域詳查時間分辨率、空間分辨率、星間鏈路性能等指標，成本主要有星座部署成本和長期運控成本。

1.1.1 全球普查覆蓋率

1) Walker星座覆蓋率

Walker星座是全球覆蓋最有效的星座,可用[(N/P/F),(h,i)]共5個參數描述[14]。(N/P/F)為離散正整數,分別為衛星總個數,分布軌道面數和相位因子F=0～(P-1)。(h,i)分別為軌道高度和軌道傾角,Walker星座默認所有衛星高度和軌道傾角相同。升交點赤經

Ωi=Ω0+i·ΔΩi=1,…,P-1

(1)

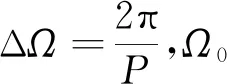
全球普查覆蓋率主要由傾角i、軌道高度h和對地觀測衛星的波束半張角θ決定,如圖1所示,全球覆蓋率為

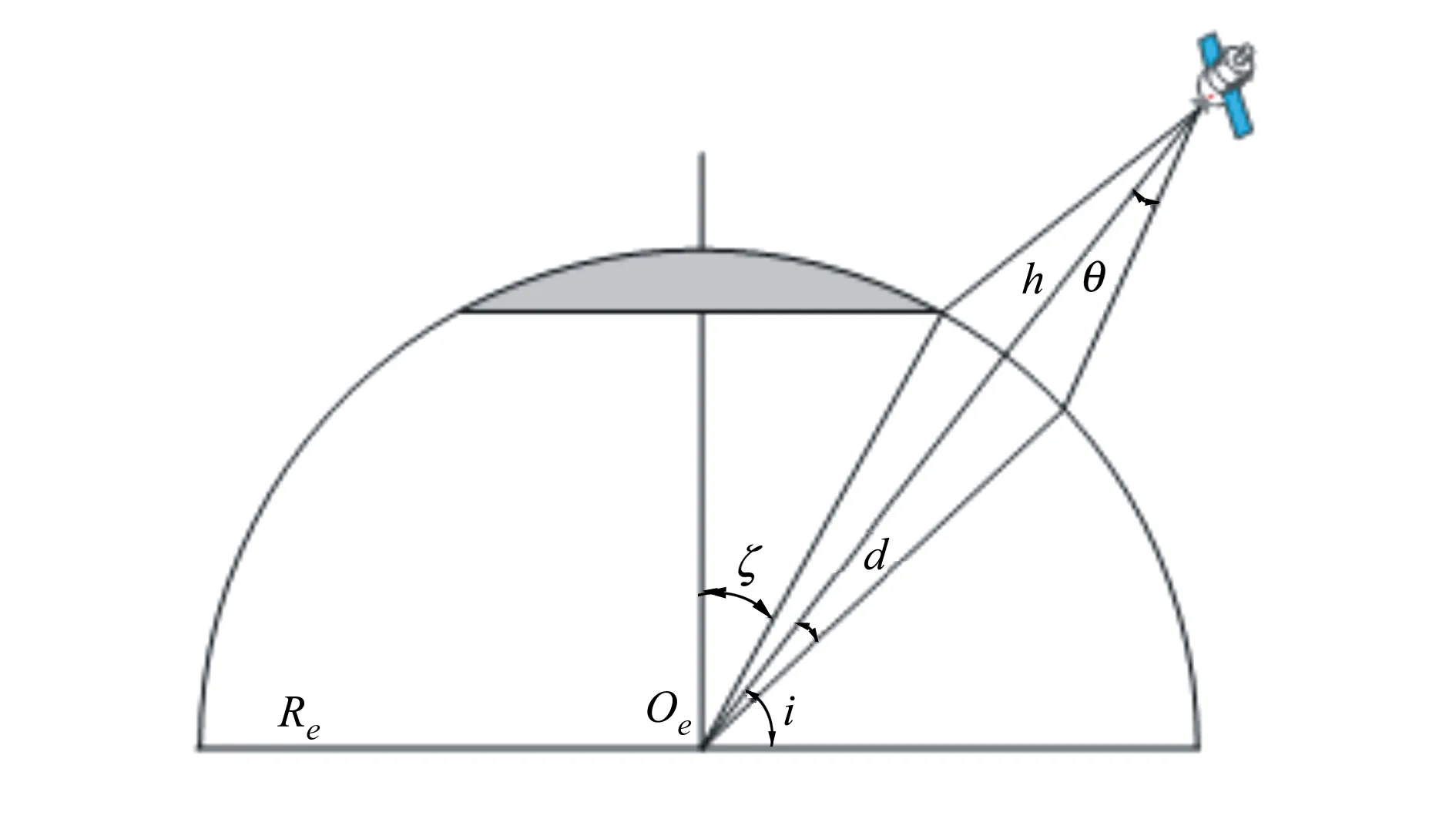
圖1 對地觀測幾何

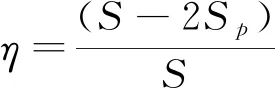
(2)

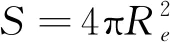
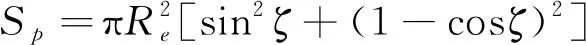
(3)

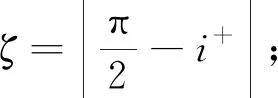
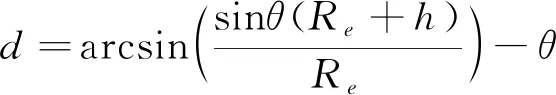
(4)

2) 異構星座覆蓋率

異構星座的全球覆蓋率需要遍歷搜索計算,涉及地表網絡劃分方法,傳統的等經緯度方法會在兩極產生密集而無用的點,等緯度帶劃分法雖然較等經緯度方法有所提高,但存在網格不均勻缺點[15]。

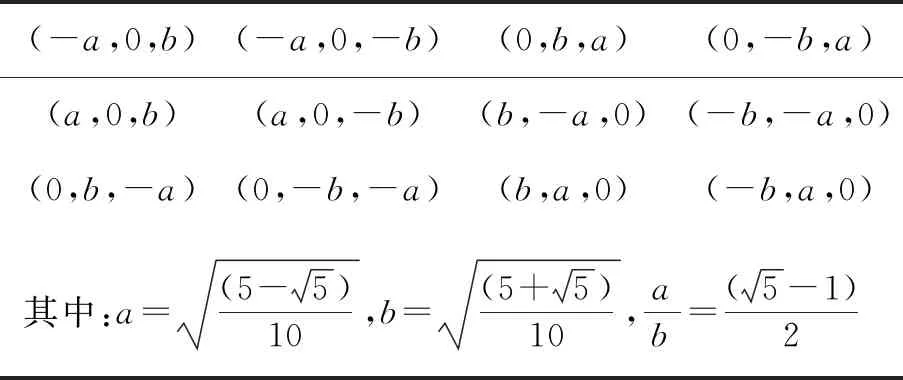
表1 正二十面體頂點坐標

正多面體是比較均勻的方法,馬原野[16]推薦正二十面體劃分方法。該方法是利用相互垂直的黃金矩陣,頂點坐標如表 1 所示。然后不斷將球面三角形4等分細化,細分3次后北極視角如圖2所示,藍色點是三角形中心點,則無旋地球(瞬時)任意點到某軌道面距離如圖3所示。

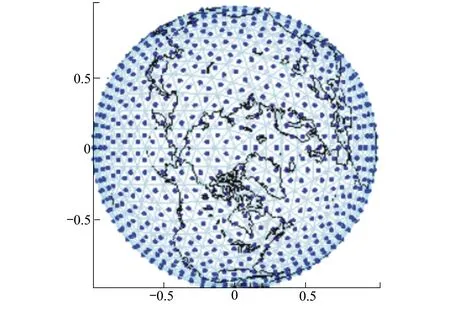
圖2 北極地區網格

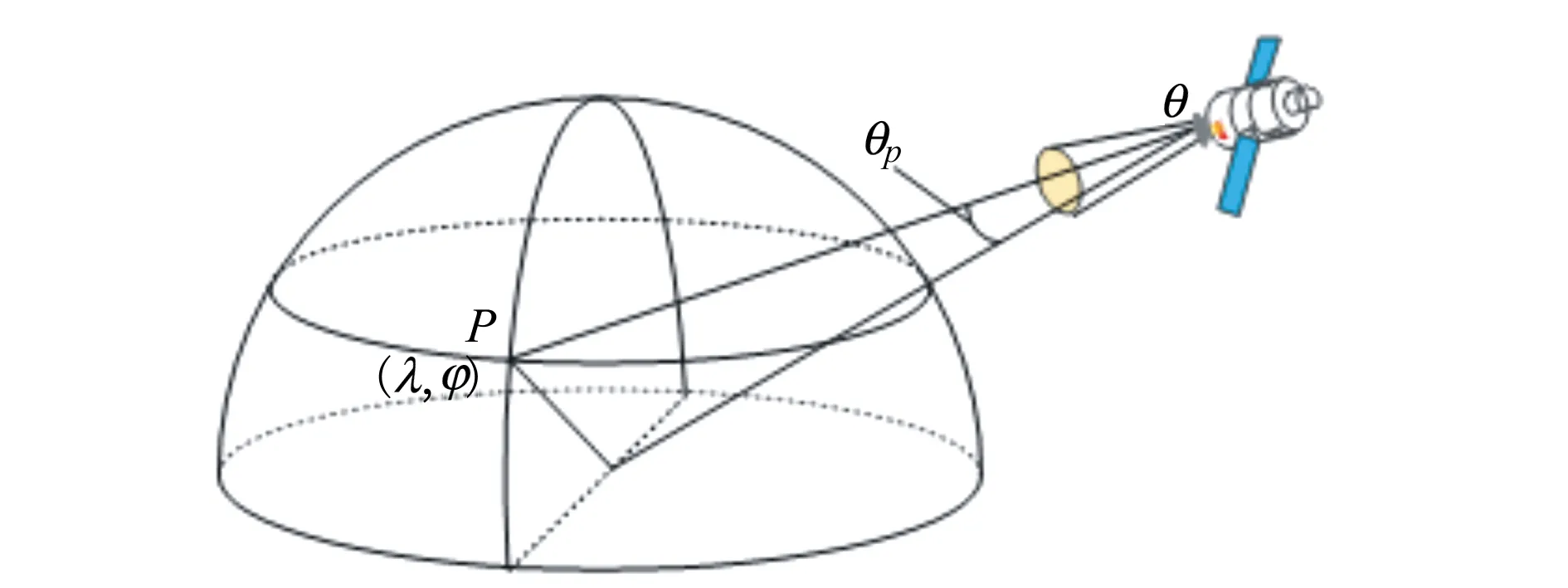
圖3 地面覆蓋帶示意圖

地面P點(地球半徑為Re)在J2000.0坐標系中可由赤經赤緯(λ,φ)表示

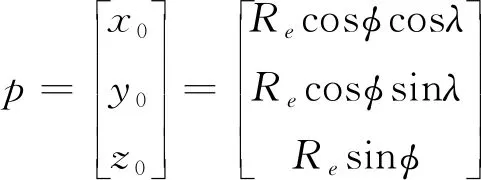
(5)

對地觀測衛星在J2000.0坐標系中位置為

psat=[x,y,z]T

(6)

在衛星載荷姿態無側擺情況下,計算地面網格中心點與衛星和地心構成的三角形中衛星所在頂點角度θp。若θp≤θ,則該地面位置能被該顆衛星覆蓋,否則,不能覆蓋。該算法需要搜索計算所有網格點中心和衛星一個周期的所有位置。在優化部署全球偵察星座時,一個重要指標即是該星座對全球的覆蓋率

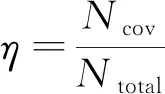
(7)

式中:Ntotal為球面網格劃分總數；Ncov為覆蓋網格數；通常η≤1。也可根據不同任務對不同區域的偵察重要性增減權值,如對于環境監測任務,兩極區域人類活動較少,可減小權值,但對于氣象預報任務,不可減小兩極區域權值。

1.1.2 觀測時間分辨率

1) 電子偵察Walker時間分辨率

電子偵察衛星工作不受陽光限制,例如,對于P個軌道面的Walker星座而言,時間分辨率有經度方法和軌道面內2個方向:

(8)

式中,ωe為地球自轉角速度。

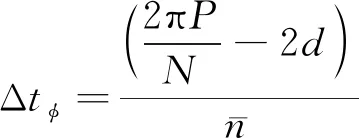
(9)

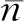
2) 異構星座時間分辨率

對于區域觀測異構光學衛星星座而言,宜采用圓軌道衛星環“并肩掃推”方式實現對特定區域的覆蓋和詳查。

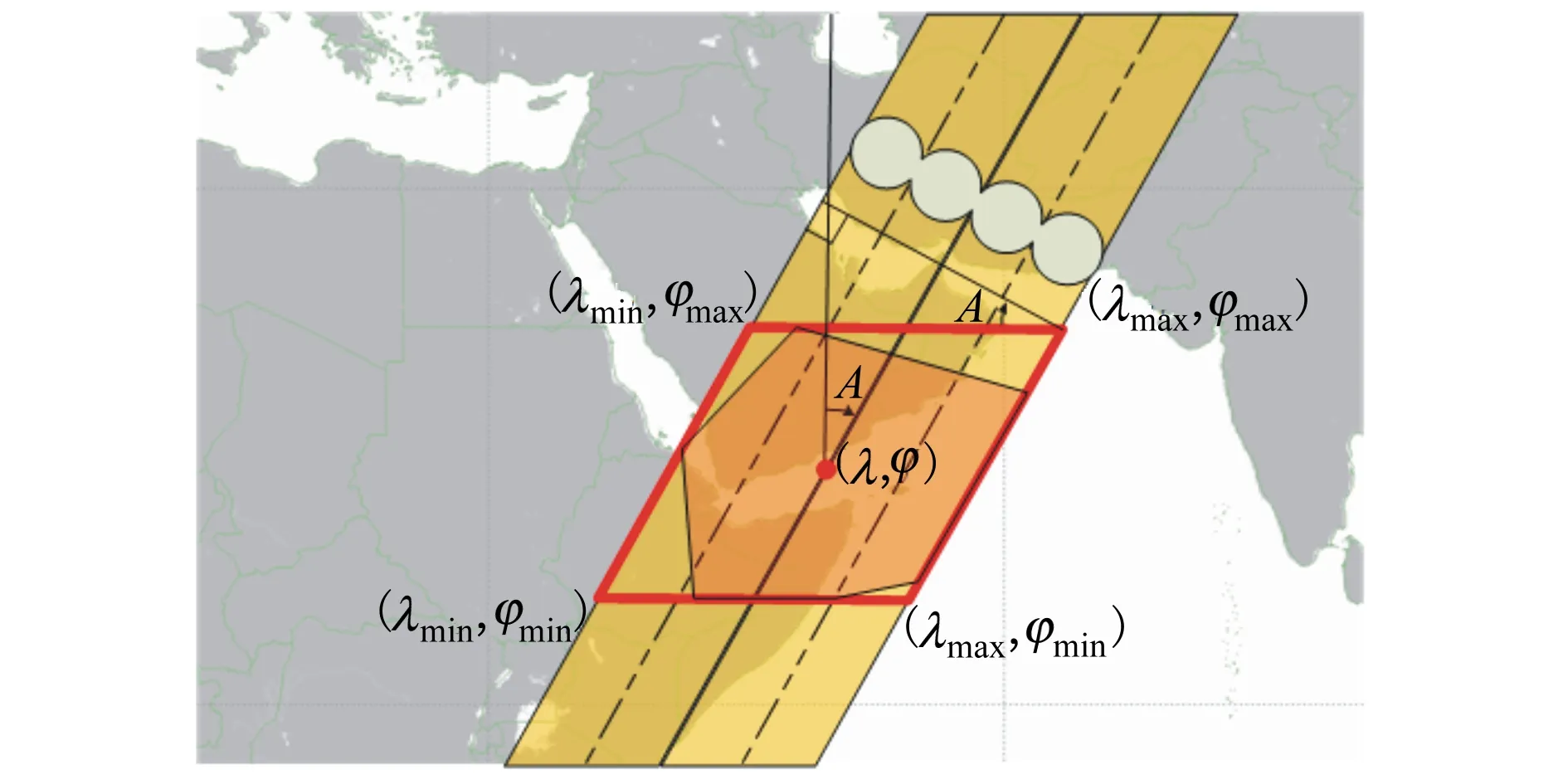
圖4 外接平行四邊形示意圖

首先,將被觀測區域以一個外接平行四邊形包圍,如圖4所示為降軌弧段觀測平行四邊形,頂點坐標經緯度最大最小值分別為(λmin,λmax,φmin,φmax)。一般而言,利用太陽同步軌道上的近地光學成像衛星實現區域高分辨率詳查,由運載火箭能力和載荷質量共同決定的軌道高度,軌道高度又決定太陽同步軌道的傾角,則外接平行四邊形傾斜方位角為

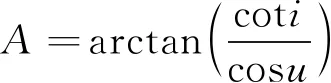
(10)

式中,u為平行四邊形中心對應緯度幅角,由該點緯度φ和軌道傾角計算得到。

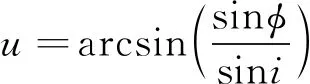
(11)

1.1.3 空間分辨率

對地觀測載荷傳感器主要有雷達、光機掃描和電荷耦合器件(charge couple device,CCD)等,雖然各自原理不同,但其空間分辨率Ersl都與瞬時視場θ(或孔徑)和軌道高度h相關

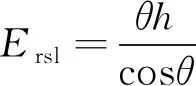
(12)

式中,θ與傳感器尺寸和掃描儀焦距(或成像板像元矩陣規模)相關,其性能品質與組成器件相關,高性能意味著成本高對電源系統需求大,一般在衛星總體設計時協調衛星成本、承力結構、電源系統和熱控系統等標準化綜合設計。若載荷確定后,空間分辨率只與軌道高度相關[17]。

1.1.4 星間鏈路指標

星座長期運控成本主要來源于構型保持控制和數據傳輸。在星座設計之初就考慮星間鏈路數傳不僅是實現遙感信息即拍即傳需求的重要手段,也是減小數傳成本的有力措施[12]。如果中軌道星座星間鏈路能全天候覆蓋低軌衛星,建立中-低軌道星間鏈路,則會有效減小長期運控成本[18]。僅考慮幾何關系的同平面等高度相位均布的圓軌道星間鏈路要求軌道高度和衛星數量存在以下關系

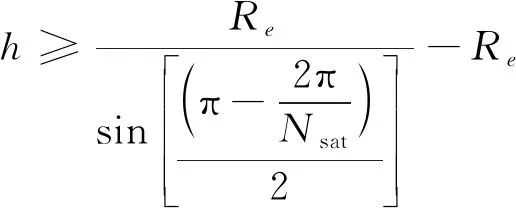
(13)

(13)式取等號時,設Re=6 378.137 km,則有Nsat=3,h=6 378.137 km;Nsat=4,h=2 641.9 km;Nsat=5,h=1 505.7 km;Nsat=6,h=986.7 km;Nsat=7,h=701.1 km;Nsat=8,h=525.5 km。

1.1.5 星座部署成本

星座部署成本主要由衛星數量和單星成本組成

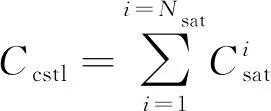
(14)

單星成本由衛星平臺、載荷和平均發射入軌成本(是否一箭多星)等因素決定

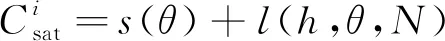
(15)

式中：s(θ)為衛星平臺和載荷的成本；在同等遙感像元成像品質假設下,θ大意味著遙感像元陣列數量多,則衛星平臺成本也高；s(θ)∝θ；l(h,θ,N)為平均發射部署成本；若θ較大,載荷和衛星平臺均大,只能單星發射或一箭雙星；h較大時,需要成本更高的火箭；若(h,θ)都較小時,可以一箭多星發射,平均到每顆星的成本會階梯性減小。所以存在最佳的(h,θ,N)組合使Ccstl最優。對于衛星數量較多的星座,宜采用已成標準的衛星平臺和可批量生產的有效載荷,并設計軌道高度一致,傾角相同的Walker星座構型。在地面分辨率要求約束范圍內,可在一定程度上提成軌道高度以獲取較大的覆蓋角,但前提是運載火箭可以承受。

1.1.6 星座構型保持代價

一般星座設計壽命超過10年,不同軌道構型保持控制頻次不同,控制策略又分為相對保持和絕對保持,后者燃料消耗代價大于前者,會減少衛星壽命[10]。混合星座往往包含2個以上星座,如果2個星座由于軌道參數差異導致漂移,往往最初的構型無法保持,且會引起數傳節點路由分配重構問題[19]。文獻[11]建議混合星座應分開設計,再考慮不同星座層間星間鏈路數傳節點問題。這樣,每個星座受攝軌道參數漂移情況相近,相對保持代價較小。而不同星座間數傳可以設置層間路由協議。

1.2 約束條件

星座設計約束條件一般有環境約束、任務目標約束、有效載荷約束和星座構型保持約束等,約束條件除在設計參數區間限制外,有時也可通過一定的手段轉化為設計目標指標。

1.2.1 Van-Allen帶

南北緯40°～50°之間,高度范圍分為兩段:內帶1 500～5 000 km,外帶13 000～22 000 km。內帶粒子的最大密度位于約3 000 km高度處,而外帶的最大密度位于約17 000 km高度。

1.2.2 大氣阻力衰減

大氣阻力在500 km以上的影響較小,所以低軌高度一般在[500,1 500]km之間。

1.2.3 地面軌跡回歸

軌道相對于地球旋轉一周的時間間隔為

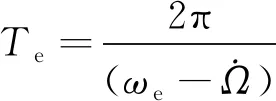
(16)

若存在既約正整數D與R使得航天器軌道周期T與Te滿足

RT=DTe

(17)

則航天器D天正好運行R圈,其星下點軌跡開始重復,稱為回歸軌道,存在回歸因子

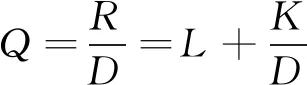
(18)

式中,L,K均為正整數,且L≤Q,01,稱為準回歸軌道。對地觀測衛星若采用回歸軌道在實際工程中能體現良好的地面重訪覆蓋性,也便于大幅降低地面運控成本。

1.2.4 載荷工作條件

僅考慮J2項攝動時,升交點赤經的進動角速度可表示為

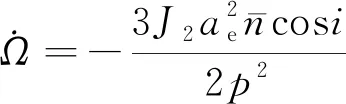
(19)

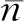
(20)

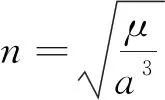
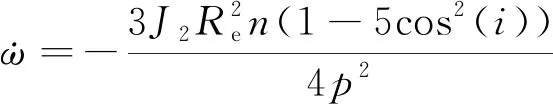
(21)

圓軌道上的衛星可以獲得一致分辨率的遙感圖像,便于后期圖像拼接處理。可見光衛星對地面目標進行攝影時,地面目標除了要滿足覆蓋要求外,還應有陽光照明。穩定的陽光高度角需要太陽同步回歸軌道。平太陽回歸年為365.242 2個回歸日,可得平太陽在赤道上移動的角速度(地球自轉)為

ωs=360°/365.242 2=0.985 6°/day

(22)

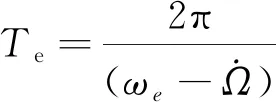
(23)

對地觀測載荷也可通過姿態側擺擴展衛星地面覆蓋帶。最大側擺角既可作為星座設計的約束條件,也可作為一種設計指標。

1.2.5 構型保持約束

由于衛星平運動和地球自轉角速度成簡單整數比時,地球田諧項攝動會對軌道半長軸產生明顯的共振影響,間接導致衛星相位漂移。衛星回歸周期D>5的準回歸軌道可有效避免共振現象。

2 中低軌混合星座

2.1 中軌星座設計

2.1.1 中軌星座設計模型

1) 設計變量

中軌軌道混合星座中中軌衛星星座應承擔全球普查和星間鏈路數傳功能,宜將電子偵察衛星部署在Walker星座上。除描述Walker星座的5個參數[(N/P/F),(h,i)]外,衛星波束半張角θ也是中軌星座的設計變量,如姿態可以側擺,相當于θ瞬時值變大

x=[(N/P/F),(h,i,θ)]

(24)

如果有地面軌跡回歸要求,可根據(17)式計算與h近似匹配的回歸因子。

2) 目標函數

對于Walker星座而言,星座構型相對保持代價較小,可在初步設計不予考慮。則剩余5個優化目標函數

(25)

式中，nisl為星座中含星間鏈路最少的衛星的星間鏈路數。由于星座部署代價指標計算涉及較多衛星、載荷、運載火箭、發射測運控市場報價情況,本文不做詳細調研,僅將衛星總數和波束半張角控制在熟知區間內。

3) 約束條件

Van-Allen內帶中粒子最大密度位于高度約3 000 km處,考慮衛星安全穩健性,一般選擇軌道高度低于2 500 km。Walker星座全球覆蓋指標要求軌道傾角接近π/2,由(4)式可知,選擇合適的軌道高度和波束半張角可使Walker星座全球普查覆蓋率保持100%的情況下,傾角在π/2附近一定區間內設計。

2.1.2 混合參數分層求解策略

圖5給出了混合參數分層設計框架,將原優化問題分為上下2層分別設計,上層選擇離散變量,下層搜索連續變量。離散變量的選取需要下層優化目標的函數值,進而給出優化的離散變量的值。

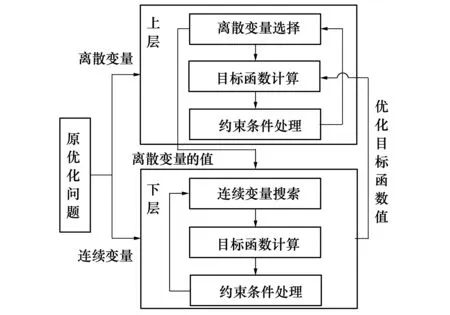
圖5 混合參數分層式設計框架

2.1.3 NSGA-Ⅱ求解

NSGA-Ⅱ(non-domination sorting genetic algorithm)是一款增加了快速非優超排序機制的多目標優化遺傳算法包[21],本文利用該算法進行連續變量多目標優化搜索。避開Van-Allen內帶中粒子密集處,假設波束半張角不大于45°,為嚴格保證J1=η=1,設軌道傾角i=90°。

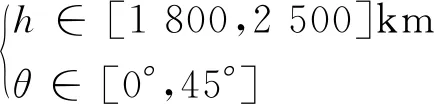
(26)

取Walker星座N/P分別為:48/12,48/16和50/10對應J2和J3的Pareto解集如圖6所示。

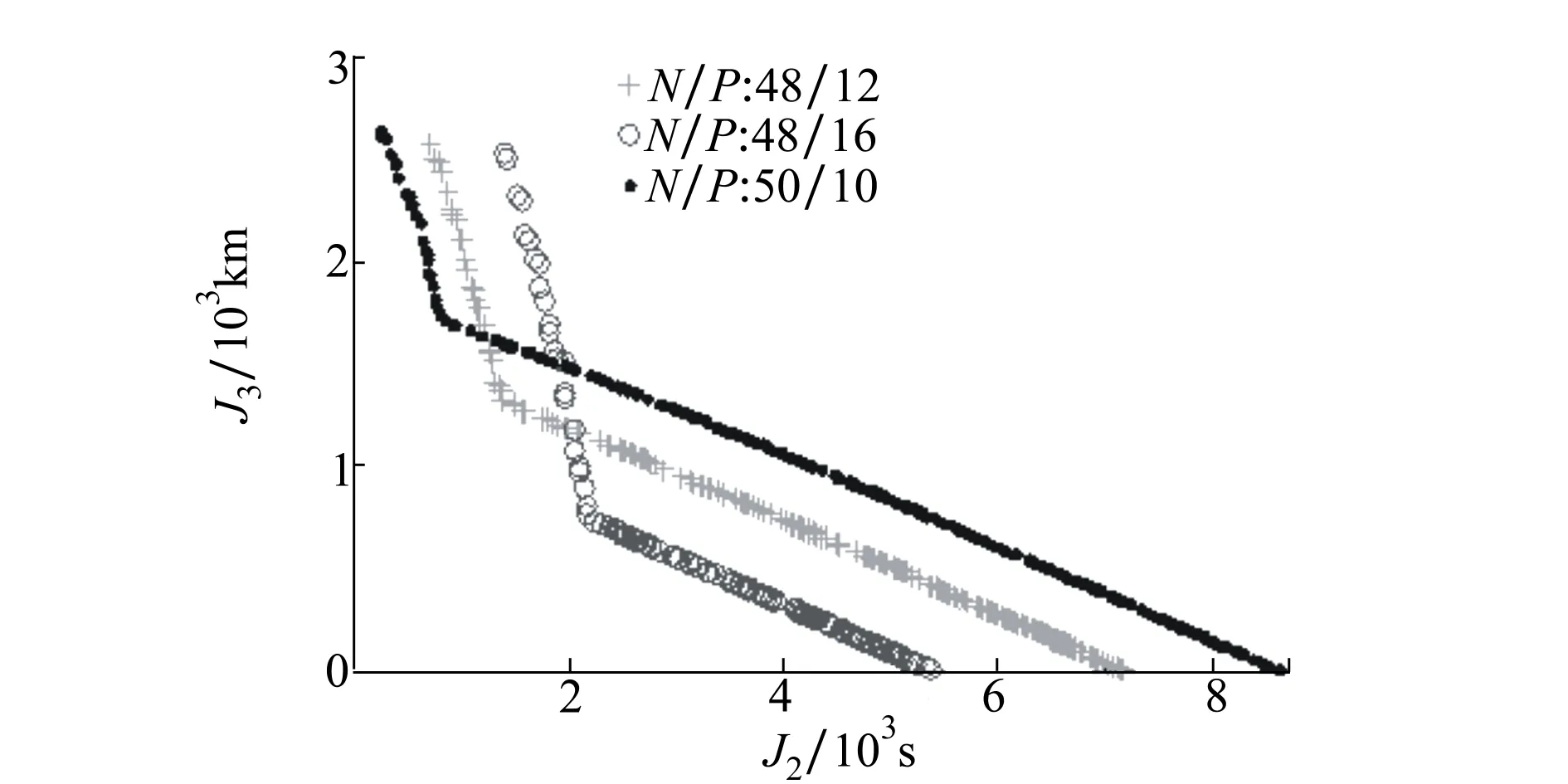
圖6 Walker星座Pareto解集

可見,Walker星座時間分辨率與軌道面數和面內衛星數都相關。當衛星總數相同或接近時,同一個軌道面內衛星顆數越多,則時間分辨率指標越低,觀測越頻繁;否則,軌道面數越多,空間分辨率指標越低,觀測信息越精確。當N/P=50/10時,無論F取什么值,所有衛星任何時刻都存在4條星間鏈路可能,J4=nisl=4。當軌道高度已知后,面內衛星數不滿足(13)式,則J4=nisl=2。星座部署代價如(14)式和(15)式所示,具體指標隨航天市場變化,本文不深入調研。

2.2 低軌星座設計

2.2.1 設計模型

相比較中軌電子偵察星座而言,低軌光學衛星星座高度一般在630～650 km之間,且采用太陽同步圓軌道,升交點赤經和相位滿足觀測區域地方時要求。除此之外,還需考慮光學衛星對地覆蓋仰角ε,如圖7所示。

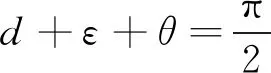
(27)

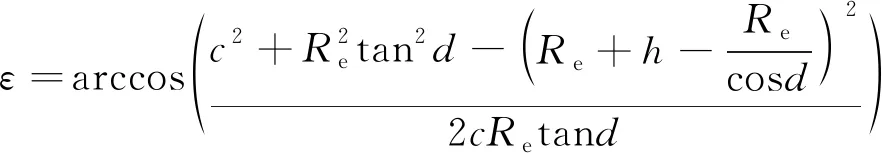
(28)

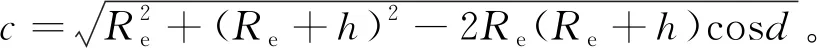
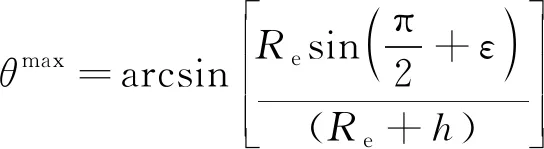
(29)

進一步,若波束半張角因光學衛星鏡頭標準化等約束出廠即給定,則軌道高度h成為決定地面分辨率的唯一參數。可見,低軌星座只需設計軌道高度和“并肩掃推”衛星環組數即可。后者直接可以計算星座部署成本和白天觀測時間分辨率。

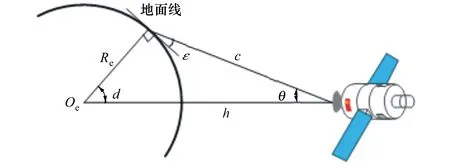
圖7 光學衛星對地觀測幾何關系

2.2.2 中低軌間鏈路

若低軌光學衛星軌道高度取極限情況hl=650 km,根據(13)式,中低軌星間鏈路存在的條件中,需更新地球半徑Re為(Re+hl)。若N/P=50/10時,軌道面內5顆衛星,需軌道高度hm>1 659.118 km,則中低軌間存在“永久”星間鏈路幾何可能。

2.3 中低軌混合星座算例

優先考慮軌道回歸特性,中軌Walker星座取圖6中N/P: 50/10 Pareto解集中h=2 165.6 km,θ=

0.137 97 rad。

考慮中軌衛星可能攜帶光學載荷,考慮太陽同步軌道傾角i=1.849 53 rad,則J1=95.11%,J2=7 318.8 s,J3=300 km,J4=4。并取F=1。以索馬里海灣為假設詳細查看目標,取太陽同步軌道高度為645.151 km,每天飛行14.75圈,1組4顆衛星“并肩掃推”。則中低軌混合星座如圖8所示。

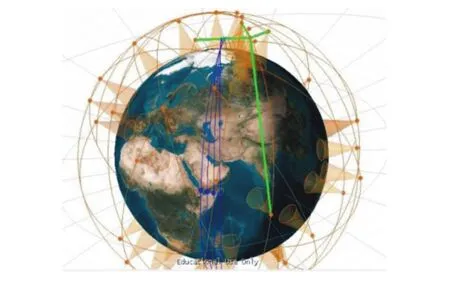
圖8 中低軌混合星座星間鏈路

3 高低軌混合星座

3.1 高軌星座的設計

高軌指軌道高度大于Van-Allen帶外帶(約25 000 km)高度以上的軌道。早在1945年,Clarke指出在地球靜止軌道上等相位間隔放置3顆衛星,就可以實現全球兩極以外的覆蓋,地球靜止軌道衛星高度h=35 786 km,設計變量為衛星個數、波束半張角、定點經度。

3.2 高低軌混合星座算例

當高軌衛星個數為3時,保證赤道全覆蓋波束半張角為8.05°,分別定點112°E,-128°W和-8°W,則全球覆蓋率J1=74.392%;覆蓋區域時間分辨J2=0,未覆蓋區域時間分辨率J2=∞;高軌衛星空間分辨率較低,取決于載荷功能,以地球靜止軌道構成的星間鏈路可以對低軌衛星全天候覆蓋。為提高地面全球覆蓋率,在保證同等空間分辨率情況下,增大覆蓋幅寬成本會顯著提高,也可以通過增加衛星數量彌補。當高軌衛星個數為4時,波束半張角仍為8.05°,分別定點22°E,112°E,-68°W和-158°W,則全球覆蓋率增大J1=82.7%,部署成本增大。

4 結 論

本文提出了對地觀測混合星座性能指標、約束條件和多目標優化設計方法，驗證算例表明：混合星座可以同時滿足對地觀測多種性能指標要求；分層多目標優化能有效求解混合星座Pareto解集，便于方案論證和擇優；利用中低軌混合星座和高低軌混合星座均可達到基本設計目標。初步分析：中低軌混合星座需要衛星數量較多，抵抗衛星失效能力強，星間鏈路距離較短，便于低功率數傳；而高低軌混合星座衛星數量少，需要較高的數傳功率；中低軌混合星座和高低軌混合星座優劣性還需進一步調研商業衛星、載荷和航天發射部署成本，補充完善成本函數具體數值后進一步計算比較。