基于敏感性分析的協方差隨機子空間方法參數優化

劉 威，楊 娜,2，白 凡,2，常 鵬,2

(1.北京交通大學土木建筑工程學院，北京100044；2.結構風工程與城市風環境北京市重點實驗室，北京100044)

對于大型工程結構，通過環境激勵[1-3]的工作模態分析(operational modal analysis，OMA)既能確保結構的安全，還能降低維護和管理的成本[4]。通常將環境激勵視為平穩白噪聲，基于這一信號輸入假定以及線性結構分析的前提，可僅通過輸出響應進行結構模態識別。在眾多時、頻域識別方法中，隨機子空間法(stochastic subspace identification，SSI)屬于現代譜分析的范疇，為參數化的計算方法，憑借較強的魯棒性和有效性而被廣泛使用[5]。

基于統計概率意義的多維數據模態分析，SSI具有同時處理多維數據特點[6]。由于其直接利用測試得到的響應數據構建計算結構模態參數的矩陣，避免了傳統的模態識別方法中采用傅里葉變換造成的譜泄漏等問題。識別過程中根據算法不同可分為數據驅動隨機子空間(data-driven stochastic subspace identification，SSI-Data)及協方差驅動隨機子空間(covariance-driven stochastic subspace identification，SSI-Cov)。由于前者涉及投影矩陣的計算，計算效率較低，因此本文選擇SSI-Cov進行研究。

SSI-Cov 中涉及一些重要參數，如系統階數N、Hankel 矩陣中過去輸出子矩陣的行塊數g和未來輸出子矩陣行塊數h、Toeplitz 矩陣的行塊數i和列塊數j等[7]。其識別模態參數的精度不僅取決于環境因素的影響，還依賴于人為選擇參數的合理性[8]。合理的參數選擇是準確識別結構模態的前提[9]，而準確識別結構的模態對于結構的健康監測及損傷評估至關重要。

因此，對相關參數進行敏感性分析以及提出建議取值對模態參數的準確識別具有重要意義。此外，目前關于利用SSI-Cov 對藏式古城墻進行模態識別的研究相對匱乏，并且用于SSI-Cov 的參數選擇研究更是鮮有報道。本文基于敏感性分析，結合一經典數值算例分析了系統階數N及Toeplitz 矩陣行塊數i對模態識別過程中穩定圖及計算結果的影響規律。提出在利用SSI-Cov進行模態識別過程中，可引入奇異熵增量理論確定系統階數N，并給出i的建議取值范圍。最后根據藏式古城墻模態識別的應用，說明了本文所研究的參數優化方法可準確識別結構的動力特性。

1 協方差隨機子空間算法

SSI-Cov 基于隨機狀態空間模型[6]，首先將響應數據表達為Hankel矩陣，然后通過計算響應數據的協方差序列組成Toeplitz 矩陣，最后通過對Toeplitz 矩陣進行奇異值分解和特征值分解得到系統矩陣，從而完成結構的模態參數識別。

Hankel 矩陣定義為：

對于離散系統，最終只需要求出系統矩陣A及輸出矩陣C即可完成模態參數的識別，其中C為 Γi的前l行。

模態參數識別過程中，穩定圖法廣泛應用于真假模態的鑒別。由于實際工程結構的系統階數往往未知，因此通常假定系統階數為Nmin至Nmax。系統的特征值兩兩共軛，階數必須為偶數。通過將計算結果繪制在二維坐標圖上(橫軸為頻率、縱軸為系統階數)，從而形成穩定圖[14]。其中，對于相鄰系統階數為2n和2n+2下的識別結果，需要進行穩定準則(式10(a)～式10(c))判斷，只有滿足穩定準則的模態結果才繪制在穩定圖上。

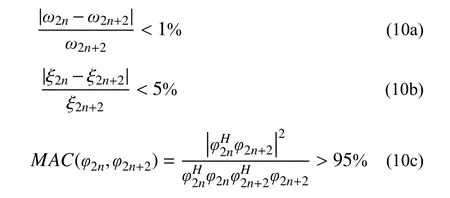
式中：H為Hermit 轉置；MAC為模態置信因子[11]。

2 數值模型

為了研究SSI-Cov 的關鍵參數對模態識別的影響，基于MATLAB語言設計程序，通過參考相關算例[15]建立一個5自由度質量-彈簧-阻尼系統的數值模型(如圖1所示)。

圖1 5自由度質量-彈簧-阻尼系統模型Fig.1 A 5-DOFmass-spring-dashpot system

模型中每個單元質量、剛度、阻尼系數分別為：mn=50 kg，kn=2.9×107N/m，cn=1000(N·s)/m。通過特征值分析，模型前5階頻率、阻尼比以及振型系數理論值分別，如表1、表2所示。

表1 模型理論頻率和阻尼比Table 1 Theoretical values of model frequency and damping ratio

利用MATLAB對首個質量塊m1輸入高斯白噪聲激勵，采樣頻率700 Hz，采樣時間50 s，各通道采集的數據長度為35 000。提取各質量塊輸出信號如圖2所示。

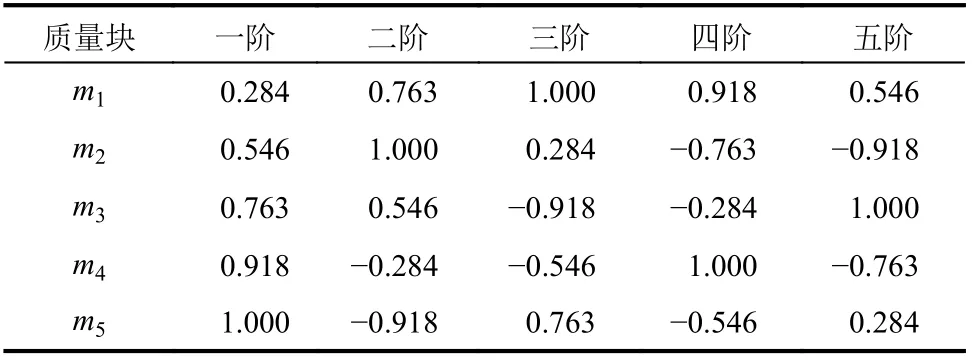
表2 模型理論模態振型Table 2 Theoretical value of modal shape of the model

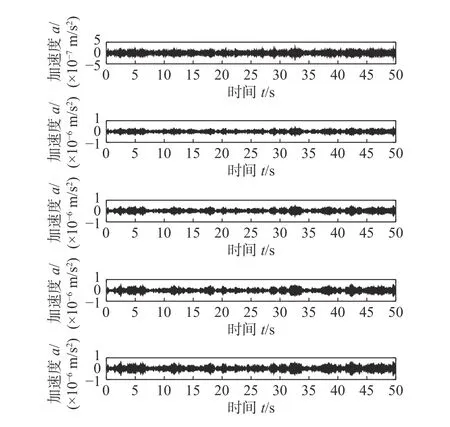
圖2 白噪聲下各質量塊輸出信號Fig.2 Output signal of each massblock under whitenoise

3 SSI-Cov 算法的模型修正及參數優化

利用SSI-Cov 進行系統識別時，是基于構建的數學模型與測量數據的擬合，以提取未知的模型參數。通過對Toeplitz 矩陣T1|i進行奇異值分解以及對系統矩陣A進行特征值分解，從而完成未知模型參數的計算。

在利用SSI-Cov 進行模態識別涉及的參數中，j應趨于無窮大，然而由于測試數據長度不可能為無限，為充分利用所測試數據，設數據總長度為s，則可得：

在對li×li維的矩陣T1|i進行奇異值分解時可知i與N在算法上需要滿足以下關系：

由式(12)可知，當系統階數N確定時，i的選擇存在一個下限值。但實際應用中，當結構基頻f0相對于采樣頻率fs較低情況下，此時i又設置的較小時，會使得Hankel塊矩陣中的輸出協方差數據信息不全，從而導致部分模態信息的缺失。因此，Reynders[16]通過不確定性分析給出了i的建議值，令 β=fs/f0，則：

本文主要針對N、i這兩個自定義參數的選擇對計算精度的影響展開分析。由于在對Toeplitz 矩陣進行奇異值分解以及對系統矩陣進行特征值分解過程中涉及到逆問題的求解，故引入條件數κ來衡量數值誤差對識別精度的影響：

式 中，λ1、λN分 別為Toeplitz 矩陣T1|i(系統 矩陣A)中的第1個和第N個奇異值。

根據穩定圖的工作原理，為了準確量化模態識別的穩定性，通過計算識別結果中頻率(阻尼比)的總變異系數δF|D作為評價指標：

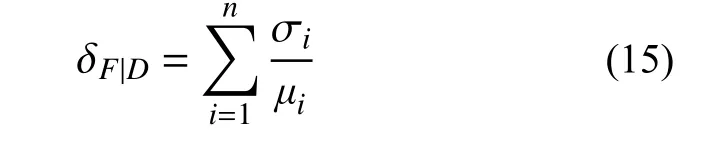
式中：n為目標識別模態的階數； σi、μi分別對應第i階模態在Nmax階下計算結果的標準差和均值。

3.1 系統階數N

本數值模型中，目標識別模態為系統的前5階，即n=5；理論系統階數為10。為分析參數N對識別結果的影響，結合式(13)暫取i=3β ≈60，j=s-2i+1=34881。

由于噪聲的影響不可避免，使得高階的原本等于零的奇異值不完全等于零，從而無法直接通過對Toeplitz 矩陣進行奇異值分解確定系統階數。在使用穩定圖方法時，要先假設一個較大的系統階數N，N的選取是否合理，直接影響穩定圖的效果：取值偏大，導致穩定圖中出現較多虛假模態；取值較小，則發生系統真實模態遺漏。因此，設置最大系統階數為Nmax∈[6,42]，且公差為4的等差序列。

圖3～圖5分別給出了在不同系統階數下(N=10、26、42)識別結果的穩定圖、條件數及相應的變異系數。其中，對于該數值算例，頻率識別精度相對較高，故僅針對阻尼比變異系數進行比較；另外，為了分析計算精度與變異系數之間的關系，同時在圖5中加入阻尼比總誤差，即所識別的各階阻尼比與理論值的絕對誤差的平均值，其中所識別的各階阻尼比是指穩定圖各極軸中對應阻尼比的平均值。

圖3 不同系統階數下的穩定圖Fig.3 Stability diagrams at different system orders

由圖3可知：隨著系統階數的增大，頻率穩定極軸逐漸出現數學虛假模態的干擾。部分可能的模態與數學模態相關聯而圍繞在物理極點附近形成新的極軸，從而給各階模態的準確識別帶來困難。當N=10，即等于理論系統階數時，可以發現系統的前5階模態均很好的識別，并且無數學模態出現。

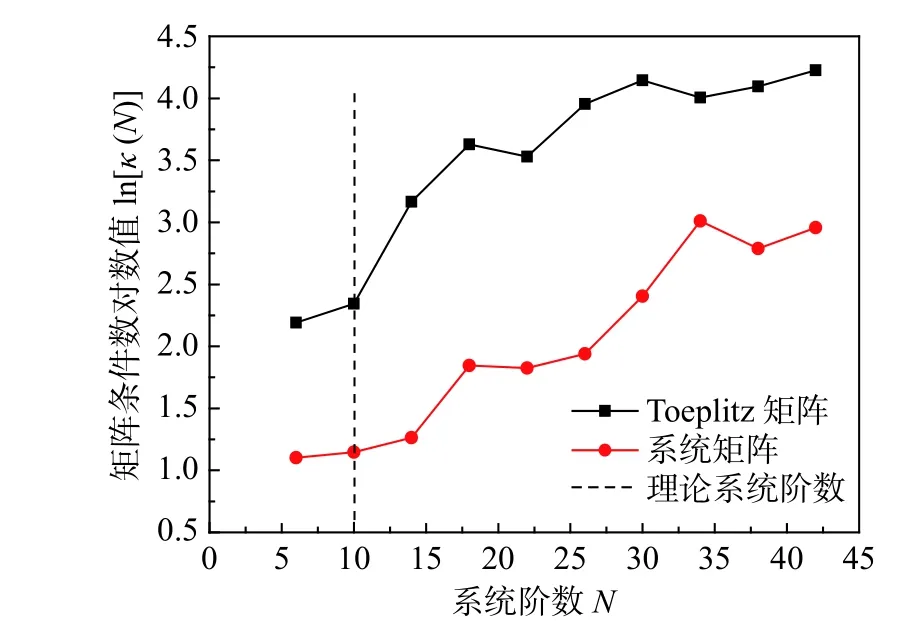
圖4 條件數隨系統階數的變化規律Fig.4 Variation law of condition number with system order

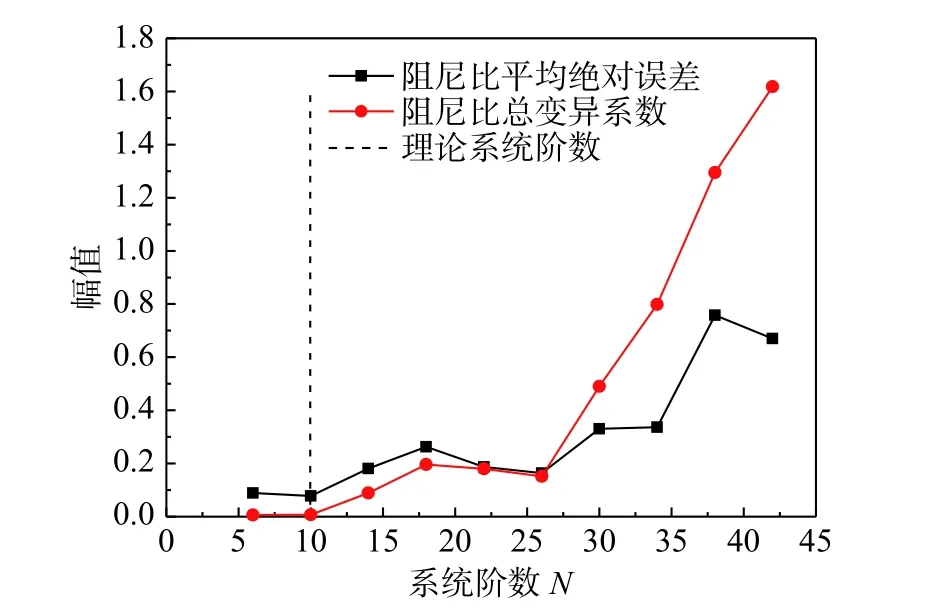
圖5 阻尼比識別結果變異系數及平均誤差Fig.5 Coefficient of variation and average error of damping ratio recognition results

條件數反映了逆問題求解過程中線性方程組的病態與否。當條件數越小，求解精度越高，響應數據的擾動對系統的擾動越小。圖4給出了Toeplitz 矩陣以及系統矩陣A的條件數隨系統階數的變化規律，可以發現二者均隨N的增大而增大，整體呈正相關關系。

圖5根據式(15)計算了阻尼比在不同系統階數時的總體變異系數：當N＜26時，總變異系數及平均誤差均維持在相對較低的水平；當N＞26時，阻尼比變異系數急劇增大，平均誤差也越來越大。二者表現出一定的相關性，原因在于變異系數反映了不同系統階數下模態識別結果的穩定性，當變異系數值較大時，往往對應于穩定圖中出現較多的數學極點干擾，從而影響模態識別精度，造成較大誤差。另外，當N=6時，第4和第5階模態出現遺漏，原因在于系統階數太低(低于真實系統階數)。

為了對系統階數進行準確識別，本文通過引入奇異熵增量理論來確定N。首先，奇異譜表示的是各個狀態變量在整個系統中所占能量的相對關系；而熵是一切事物狀態不確定性的度量，信息熵是考察信號包含信息量的有效指標之一[17-19]；因此，奇異熵對信號信噪比的變化反映非常敏感，可用于系統階數的識別。

假定系統有m個狀態，每個狀態存在的概率為pi，則該系統的熵E可表示為：

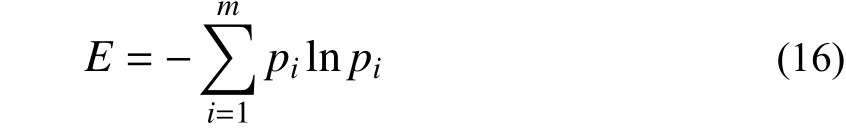
在無噪聲或高信噪比情況下，通過對Toeplitz矩陣進行奇異值分解得到其特征值對角矩陣為：

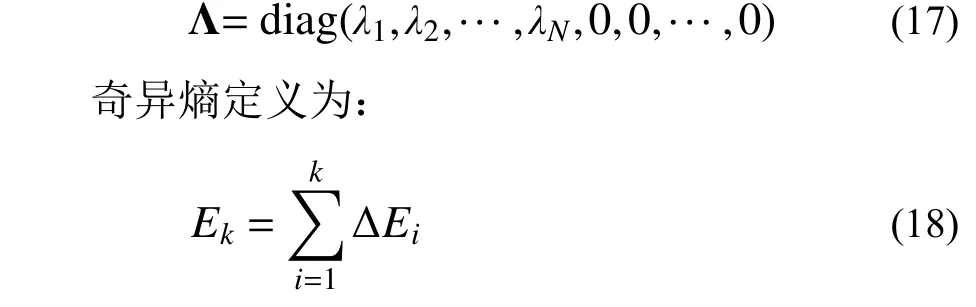
式中，k為奇異熵的階數，k≤N。ΔEi表示奇異熵在階數i處的增量，其表達式為：

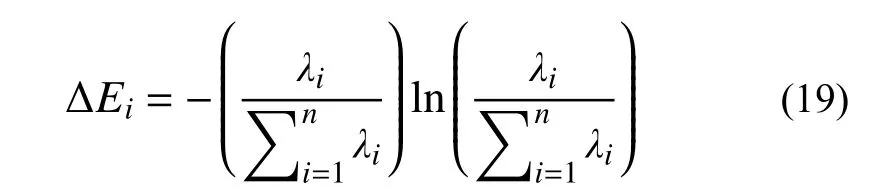
當奇異熵增量降低到漸近值時，信號的有效特征信息量才算基本完整；此時，對于同一信號，不論其信噪比高低，對應的奇異譜階數完全相同。基于奇異熵這一特性，當奇異熵增量趨于穩定時，所對應的奇異譜階數即可認為是系統階數。

隨著系統階數的增大，對于指定的一個系統，不同N值下的奇異熵增量計算結果相同。以N=10、26、42為例，截取計算結果的前30階進行繪圖，該系統奇異熵增量均如圖6所示。在實際工程應用中，通過對奇異熵計算一階靈敏度可以進一步直觀的觀察系統階數。由圖6可知，當N=10時，奇異熵增量的一階靈敏度降低為0，即該數值模型的系統階數為10，結果與理論值一致。

3.2 Toeplitz 矩陣行塊數i

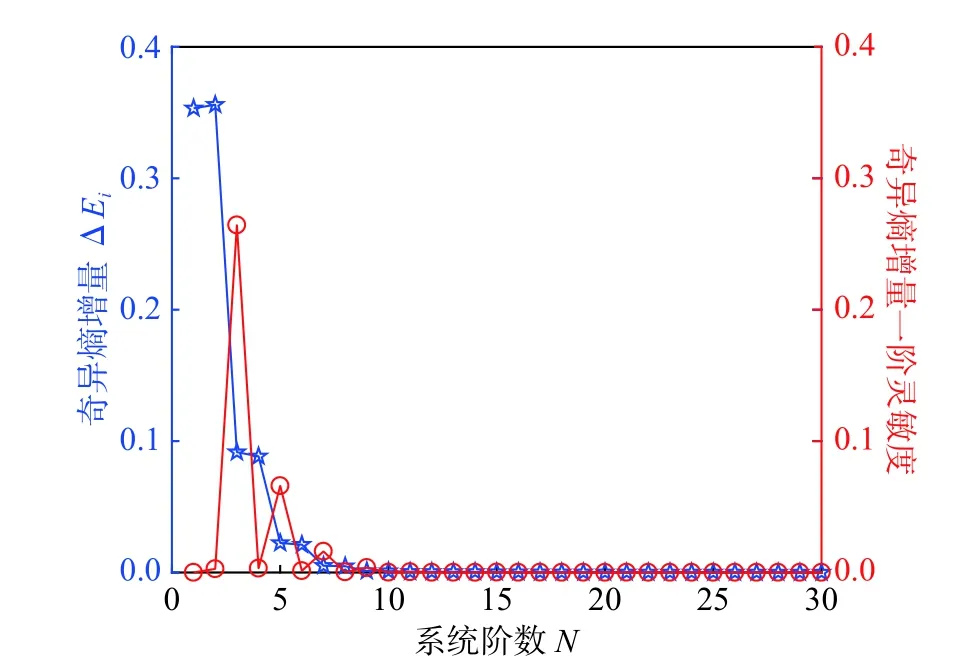
圖6 奇異熵增量及其一階靈敏度Fig.6 Singular entropy increment and its first-order sensitivity

結合式(12)、式(13)可知，當系統階數N確定，i≥max(N/l,0.5β)。即便如此，對于參數i，僅可以得到其下限值，并沒有確保子空間模型和響應數據擬合更優、穩定圖更清晰的取值范圍，而i的取值對計算結果和穩定圖的影響不可忽視[20]。因此，在數值模型和實際應用中，首先基于奇異熵理論確定系統階數N，然后通過分析i的取值對Toeplitz 矩陣T1|i(系統矩陣A)的條件數以及穩定圖識別質量的影響，分析其最優化取值區間。

根據數值算例，取N=10，i=[β:0.5β:5β]。圖7反映了不同i值對條件數的影響，即在β ～5β，Toeplitz 矩陣T1|i(系統矩陣A)的條件數對i的取值不敏感，整體波動較小。i=β 、 3β 、 5β時的穩定圖結果如圖8所示。當i＞4β時，由于i的取值過大而導致第5階模態在穩定圖上出現遺漏的現象(如圖8(c)所示)。由于該5自由度數值模型系統階數較小，僅為10階，所以在實際繪制穩定圖時N的取值也可適當大于基于奇異熵識別的系統階數。

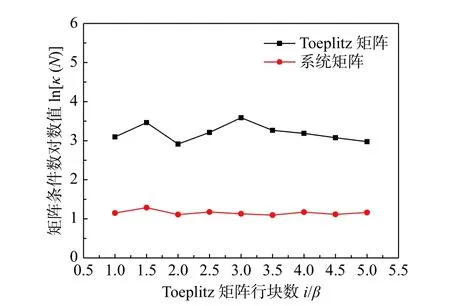
圖7 條件數隨i 值的變化規律Fig.7 Variation law of condition number with i value

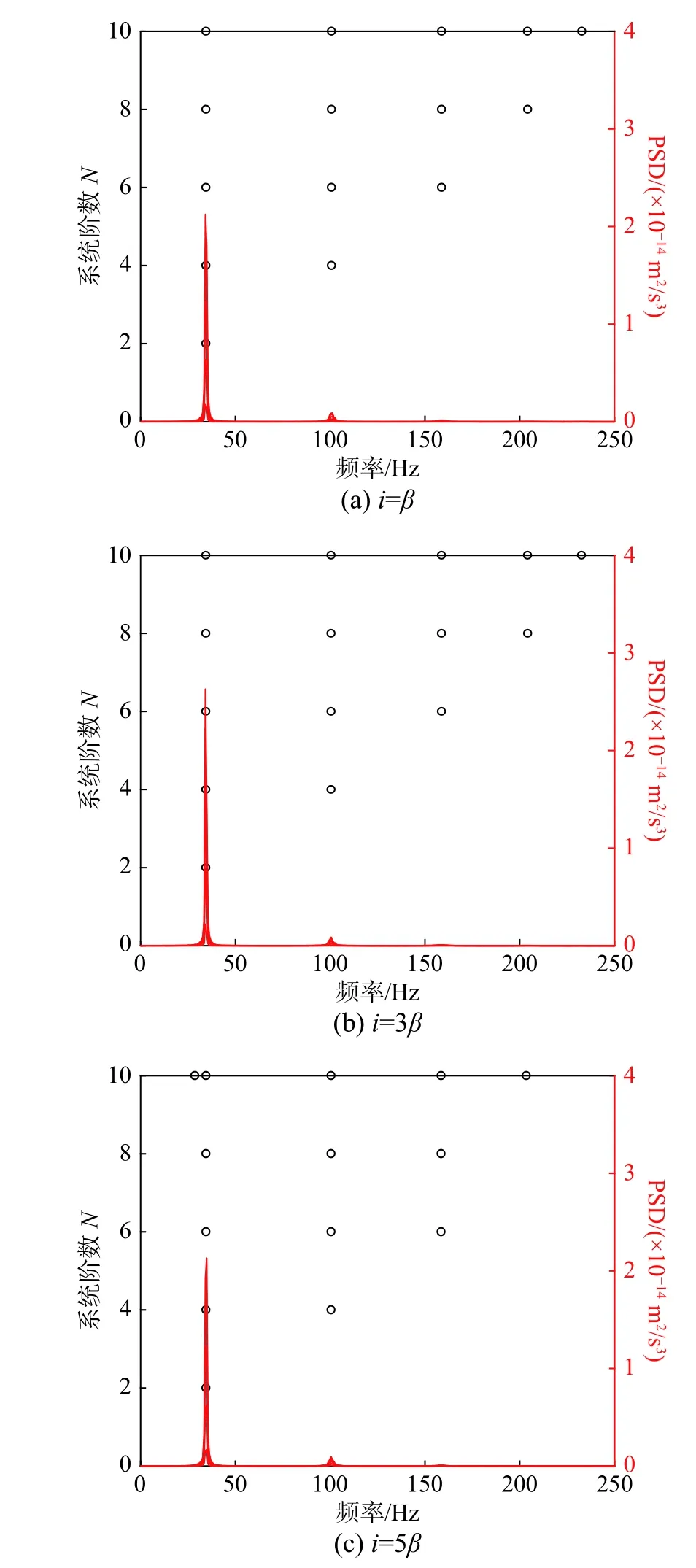
圖8 不同i 值下的穩定圖Fig.8 Stability diagramsat different valuesof i

圖9給出了阻尼比在不同i值下的變異系數及平均絕對誤差。由圖可知：識別的前5階目標阻尼比的變異系數在i=β～2β時逐漸增大，在i=4β～5β時逐漸減小，在i=2β～4β時呈現先減后增的趨勢。結合平均絕對誤差先減小后增大的規律可得：當i=2β～4β時，阻尼比變異系數和平均絕對誤差均相對較小。其中，i=3β時阻尼比的變異系數最小，為0.89%，前5階阻尼比平均絕對誤差為8.75%，前5階理論與識別的振型MAC值分別為1、1、0.994、0.996、0.993。因此，基于數值算例分析可得：當i=2β～4β時，模態識別的精度較高。

圖9 阻尼比識別結果的變異系數及平均誤差Fig.9 Coefficient of variation and average error of damping ratio recognition results

4 應用

4.1 現場測試

4.1.1結構概況

本文研究的藏式古城墻為西藏地區某典型古城墻。該城墻被門樓、塔樓分為5段。由于墻體周邊地面有起伏，從不同位置測量高度有差異，各段高度為6.0 m～6.9 m(不考慮女兒墻高度)。底部厚度為4.2 m～5.8 m，頂部為3.1 m～3.8 m。

古城墻原為夯土墻，夯土中摻入了卵礫石，后來先后在城墻內外立面各增加一層0.5 m 厚的石砌體。墻體采用收分設計，高大厚重，兩側的石砌體為方石疊壓片石的結構，沿石砌體墻面不同高度處還不規則的設置了透氣孔。根據上述建造工藝，從而形成了藏式傳統古城墻獨特的建筑風格。然而經歷數個世紀的自然災害洗禮，古城墻局部出現了較嚴重的病害，如東墻北段曾發生大面積坍塌，如圖10所示。

圖10 E 段墻發生坍塌Fig.10 Collapse of section E wall

4.1.2環境激勵測試方案

對于城墻結構，振動主要體現為平面外振動。為了獲取其平面外振動特性，從而了解各段墻體的模態信息，具體包括結構頻率、阻尼比、振型。根據結構特點以及測試條件限制，按照圖11所示的截面(A1～E2)分別對5段城墻進行加速度信號動力測試，截面選取原則為：1)對于較短的墻A、D，選擇跨中作為測試截面；2)對于較長的墻B、C、E，選擇近似三分點處；3)考慮墻體中部透氣孔分布的隨機性。

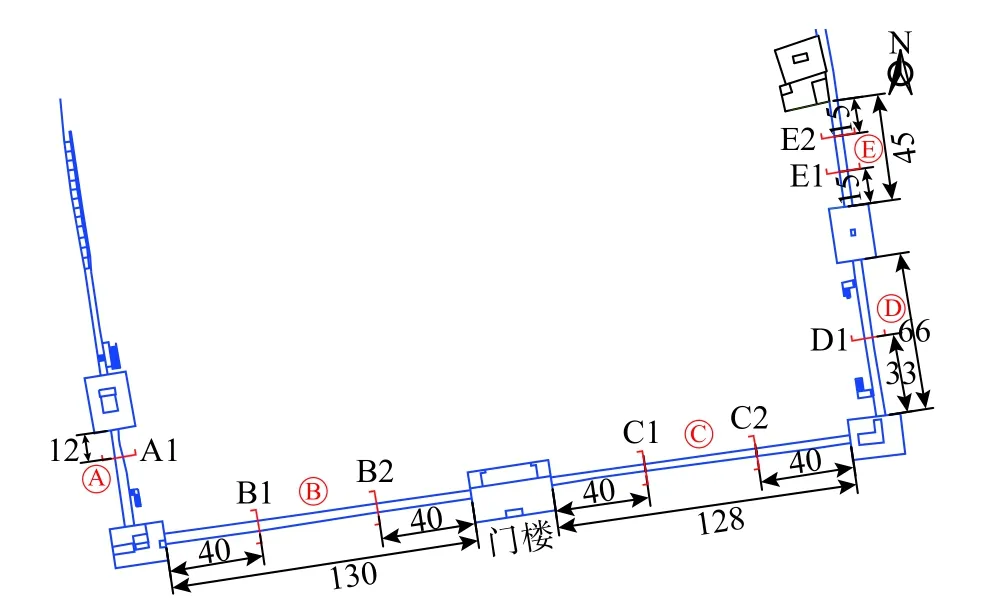
圖11 城墻測試截面示意圖/m Fig.11 Schematic diagram of the test section of the city wall

為避免對城墻結構造成影響和破壞，采用環境激勵法進行動力測試。測點布置原則為：1)結合城墻結構分布有透氣孔這一特點，各測試截面按照內側墻底、內側墻中、內側墻頂、外側墻頂、外側墻底分別布置5個測點(如圖12)；2)其中內側墻中測點優先選在1/2高處，實際布置高度均予以測量；3)測點方向布置為朝墻體內側方向，即南墻傳感器方向均為由南向北，東(西)墻傳感器方向均為由東(西)向西(東)。各測點傳感器通過快干粉固定并調至水平。

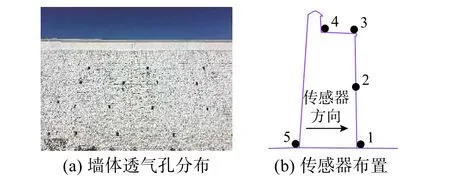
圖12 墻體透氣孔分布及傳感器布置情況Fig.12 Distribution of air permeability holesin wallsand arrangement of sensors

測試設備如圖13所示：數據采集設備為北京東方所INV3062T 四通道采集儀，測試時最多需要3臺采集儀同時工作(對于A、D兩段墻為5通道，B、C、E三段墻為10通道)；傳感器為941B型超低頻加速度測振儀，內置前置放大器功能。采樣頻率為128 Hz，采樣時長為50 min，每個測點采集加速度數據總量為384000個。測試過程中，確保附近無其他干擾激勵源。

圖13 現場測試設備Fig.13 Field test equipment

4.2 模態識別與參數分析

4.2.1系統階數N的確定

本文以E段墻為例，進行其模態參數的識別。主要針對古城墻面外振動的前3階模態進行識別，即n=3。根據頻域譜分析可知，結構基頻約為6 Hz。為分析參數N對識別結果的影響，結合3.1節的分析結果先選定i=3β ≈66，j=s-2i+1=383869，設置最大系統階數為Nmax∈[18,58]，且公差為4的等差序列。

圖14給出了N=22、38、54時的穩定圖識別結果。可以看出：隨著系統階數的增大，SSI-Cov識別的穩定圖中數學模態隨之而增多。對于識別的前3階目標模態，當N=22時物理極軸相對穩定，干擾最小；N=38時，第3階模態附近開始出現數學模態的極點；N=54時，第1階和第3階模態周圍出現較多的數學模態形成的極軸。

圖15、圖16分別為不同系統階數下，條件數及變異系數變化規律：1)Toeplitz矩陣及系統矩陣A的條件數隨系統階數的增大近似呈線性增大；2)識別結果中阻尼比的變異系數明顯比頻率大，且阻尼比變異系數隨系統階數的變化波動較大，而頻率變異性很小。

根據3.1節奇異熵理論，識別藏式古城墻的E 段墻的系統階數：該結構奇異熵增量及其一階靈敏度如圖17所示，當N在22附近時，奇異熵增量一階靈敏度趨于0，因此識別出該系統階數為22。結合圖14(a)，同時也說明了當系統階數設置的越接近實際值，基于SSI-Cov 方法識別的穩定圖越穩定。

4.2.2 Toeplitz 矩陣行塊數i的選擇

已知藏式古城墻面外振動系統階數N=22，取i=[β:0.5β:5β]。圖18反映了不同i值對條件數的影響，與數值算例不同的是：在 β ～5β，Toeplitz矩陣T1|i(系統矩陣A)的條件數隨i的增大而減小，且減小速率逐漸變緩。頻率和阻尼比的變異系數在2β ＜i＜4β時變化趨勢相對平緩，隨后急劇增長(圖19)。i=β 、3 β 、5 β時的穩定圖結果如圖20所示。當i=β時，第2階模態在穩定圖上出現遺漏的現象(圖20(a))；當i=5β時，第2階模態周圍出現數學模態干擾。綜合來看，當i=2β～4β時，既能得到清晰的穩定圖，又能滿足識別結果的數值穩定性，i的建議取值范圍與算例結論一致。

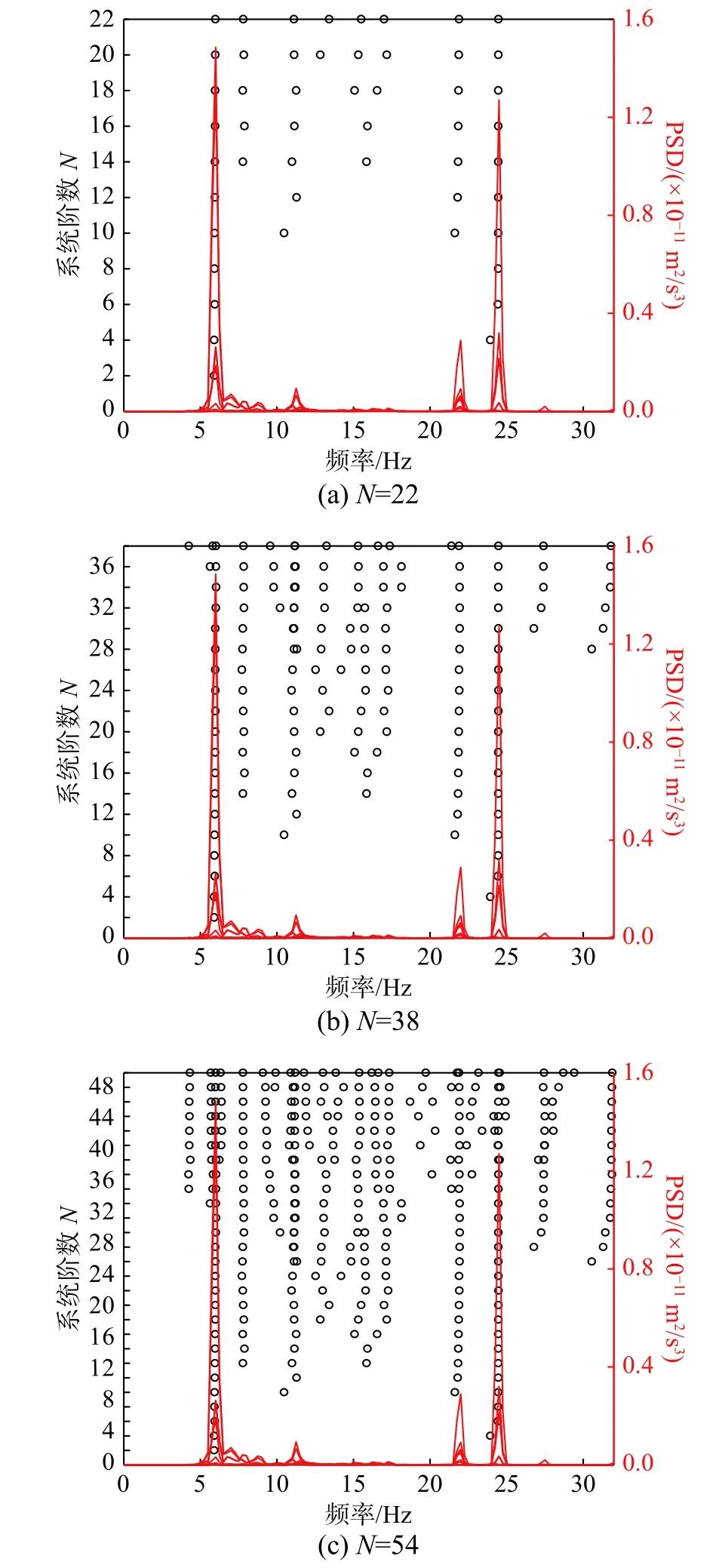
圖14 不同系統階數下的穩定圖Fig.14 Stability diagrams at different system orders

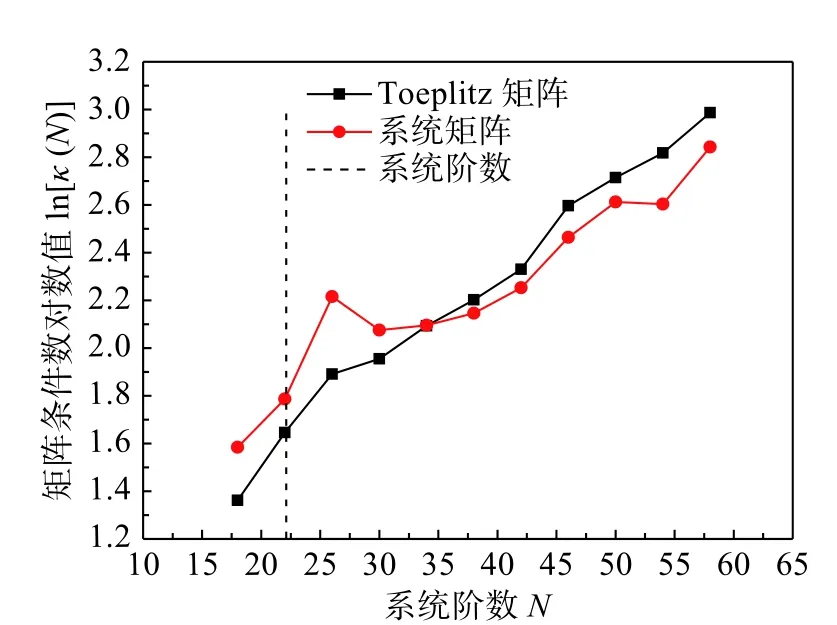
圖15 條件數隨系統階數的變化規律Fig.15 Variation law of condition number with system order

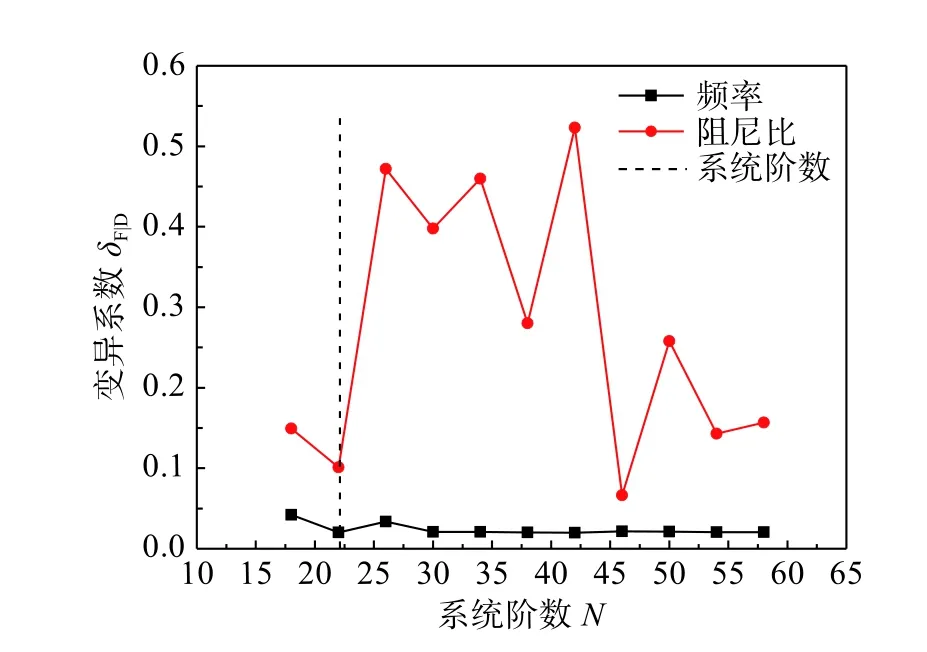
圖16 頻率、阻尼比變異系數隨系統階數的變化規律Fig.16 Variation law of variation coefficientsof frequency and damping ratio with different system orders

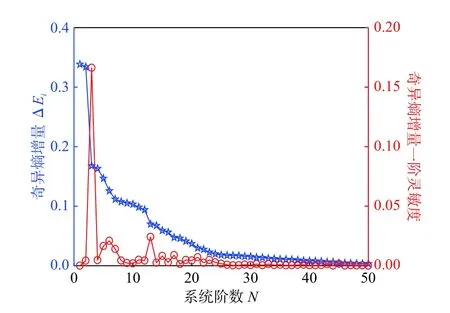
圖17 奇異熵增量及其一階靈敏度Fig.17 Singular entropy increment and itsfirst-order sensitivity

4.2.3模態識別結果

根據上述系統階數及Toeplitz 矩陣行塊數的選擇分析，再次驗證了基于奇異熵理論確定系統階數N，且i選擇為2β～4β時，可更好地識別結構的模態參數。文中針對藏式古城墻結構最終選擇N=22，i= 3β進行模態識別。表3給出了E段墻的前3階頻率和阻尼比信息。由于各段城墻兩端均連接著角樓或者門樓，故假定各段城墻兩端為固接。由于E段墻沿高度方向布置了上、中、下3處測點，沿長度方向布置了兩處截面，故僅將前兩階振型繪制如圖21所示。

圖18 條件數隨i 值的變化規律Fig.18 Variation law of condition number with i value

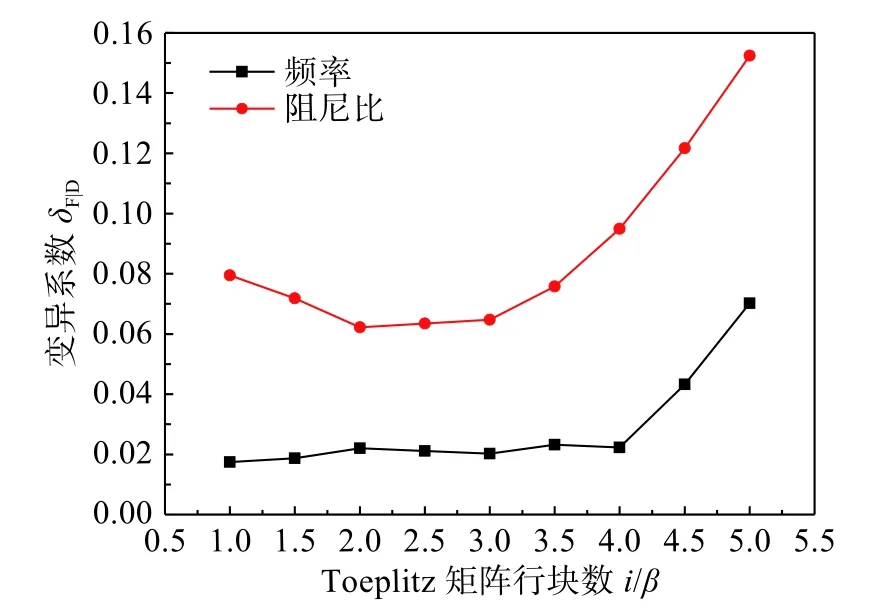
圖19 頻率、阻尼比變異系數隨i 值的變化規律Fig.19 Variation law of variation coefficient of frequency and damping ratio with i value

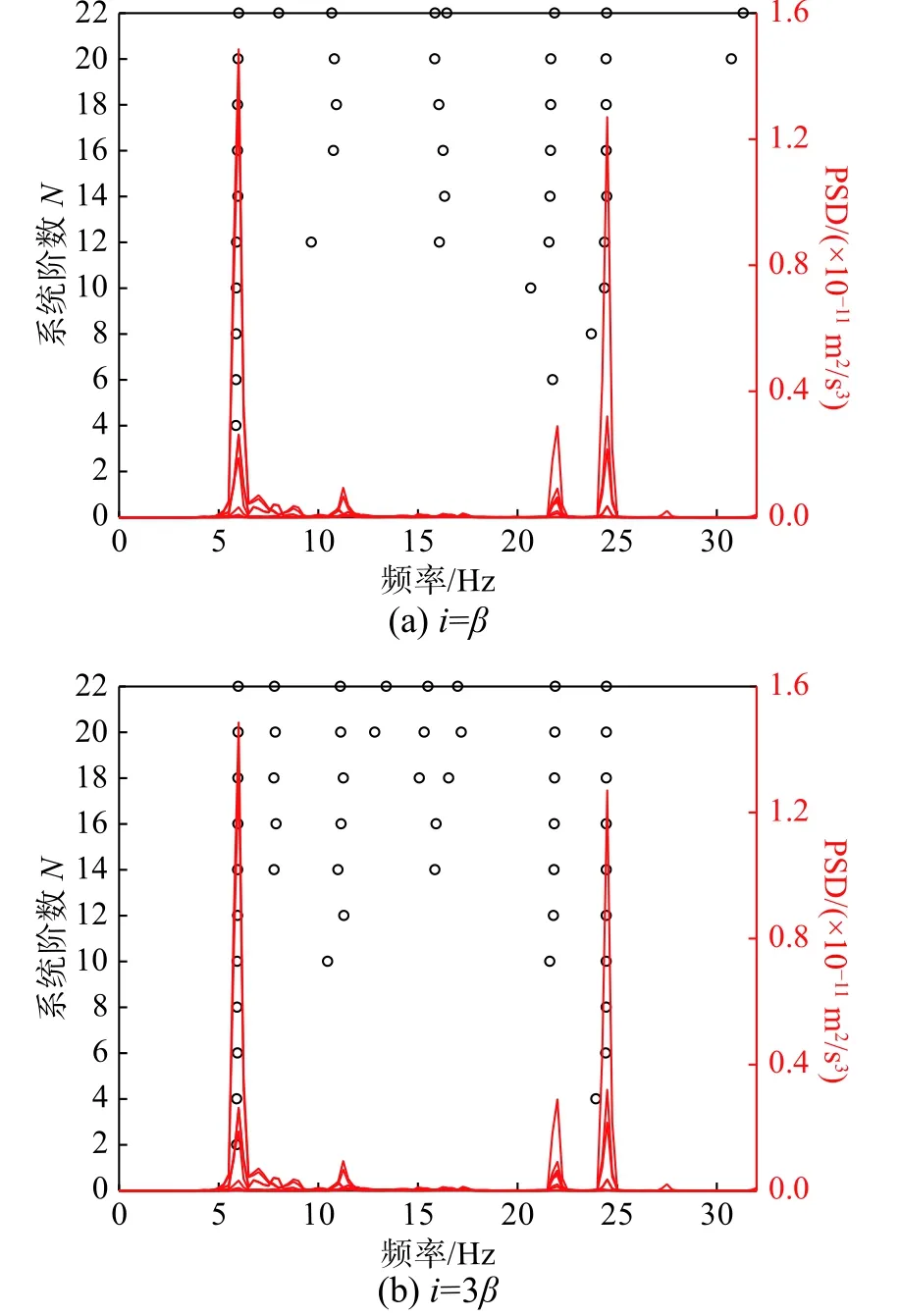
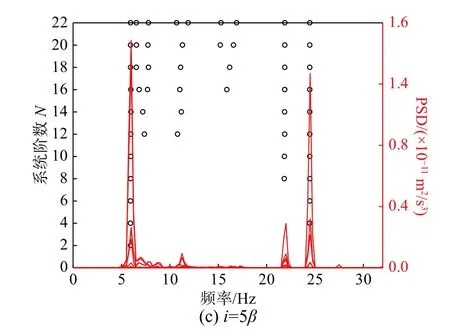
圖20 不同i 值下的穩定圖Fig.20 Stability diagramsat different valuesof i

表3 E 段墻面外振動前3階模態參數Table 3 The first third-order modal parametersof external vibration of section Ewall

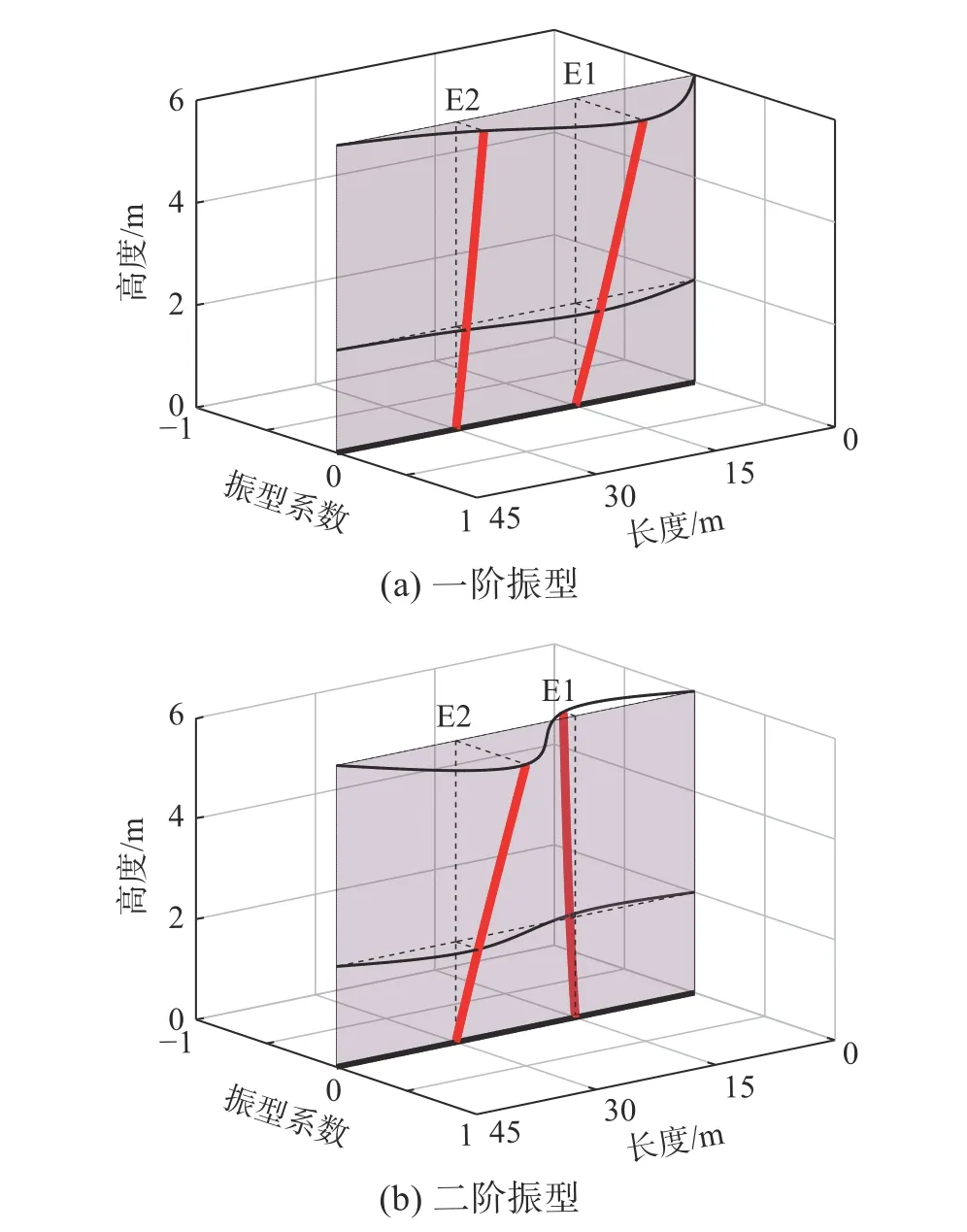
圖21 E 段墻面外振動模態識別結果Fig.21 Modal recognition results of out-of-plane vibration of section Ewall

根據圖21可知，E 段城墻面外振動的一階振型中兩截面振動方向相同，截面E1、E2均近似為彎曲型；二階振型中兩截面振動方向相反，截面E1、E2均為彎曲型，此時沿墻體縱向發生一定程度扭轉變形。

5 結論

本文通過對協方差驅動隨機子空間法中的幾個參數優化進行敏感性分析，重點研究了系統階數N及Toeplitz 矩陣行塊數i對模態識別過程中穩定圖及計算結果的影響規律。首先，結合Toeplitz矩陣和系統矩陣的條件數分析計算模態結果的精度；然后，基于模態參數識別結果的變異系數分析其與穩定圖質量的關系。利用一經典數值算例(五自由度質量-彈簧-阻尼結構)進行了驗證，進而應用于藏式古城墻結構模態參數的現場實測。主要結論如下：

(1)Toeplitz 矩陣或系統矩陣A的條件數越小計算結果精度越高；識別頻率、阻尼比的變異系數越小，對應的模態穩定圖質量越好。

(2)通過奇異熵增量理論可準確識別結構的系統階數N，奇異熵增量的一階靈敏度降至0時對應的階數即為系統階數。

(3)協方差驅動隨機子空間法中，Toeplitz 矩陣行塊數i的建議取值范圍為2β～4β ( β為采樣頻率與結構基頻的比值)。

(4)基于本文提出的參數優化方法，利用協方差隨機子空間法能有效識別藏式古城墻的動力特性，包括頻率、振型和阻尼比：識別該結構的前3階頻率分別為5.93 Hz、7.80 Hz、11.15 Hz；前3階阻尼比分別為0.0238、0.0364、0.0479。