復合加固圓形短木柱軸心受壓應力-應變關系

阿斯哈，周長東，楊禮贛

(北京交通大學土木建筑工程學院，北京100044)

木柱作為古建筑木結構最主要的豎向支撐構件，對于結構的穩定性和安全性至關重要。在長期服役過程中，由于外界自然環境因素以及木材自身生物質特性所致，部分既有古建木柱損傷嚴重甚至趨于破壞，亟需有效的方法和措施對古建木柱進行維修和加固。

FRP(fiber reinforced polymer)材料以其輕質、高強、耐腐蝕、易裁剪等特性，被廣泛應用于加固工程領域，近年來相關學者開展了眾多FRP材料加固木柱的研究與應用。周乾等[1-2]采用CFRP布(carbon fiber reinforced polymer)代替鐵箍對殘損柱根進行包鑲和墩接加固，其研究表明加固后木柱的承載力和變形性能均得到提升。許清風等[3]采用CFRP布維修加固局部受損木柱，木柱局部受損處用完好順紋木塊替換并用CFRP布包裹后，受壓承載力和延性性能得到完全恢復。此外，有學者提出了木柱表面內嵌筋材的加固方法并對其適用性展開了研究。淳慶等[4-5]采用CFRP材料(筋和板)對圓木柱進行內嵌加固，試驗結果表明加固后木柱的軸心抗壓強度有不同程度的提高；基于數據回歸，提出了內嵌筋材加固木柱的承載力計算公式。Lu 等[6]同樣采用CFRP板對膠合木柱進行內嵌加固，旨在探究該種方法的可行性。其研究結果表明木柱承載力和延性均得到顯著提升，并且得到了相應的計算模型。此外，有學者探究了木材與筋材的黏結特性，驗證了二者之間的可靠錨固性能[7-8]。外包FRP布能夠改善木柱延性，內嵌筋材可以提高木柱承載力，兩種方法相結合的復合加固則進一步提升了木柱的工作性能[9-10]。

加固木柱的受壓應力-應變模型可以指導實際工程應用，同時也是對加固木柱進行有限元分析的必要條件。邵勁松等[11-12]提出了FRP橫向加固木柱軸心受壓承載力計算公式，并結合試驗數據得到了FRP 加固木柱軸心受壓時的增量應力-應變關系模型。目前，雖然有學者提出了FRP材料加固木柱的軸心受壓承載力計算方法[9,13]，但是對于加固木柱在軸心受壓作用下應力-應變全曲線模型的研究還相對較為缺乏。

相比于FRP材料加固木柱應力-應變關系的研究現狀，FRP橫向約束混凝土柱的軸心受壓試驗與理論研究則更為充分和完善。Ozbakkaloglu 等[14]對既有的68個FRP約束圓形截面混凝土柱受壓應力-應變模型作出對比和評價，并指出Lam、Teng[15]和Tamuzs等[16]的計算模型具有更好的預測精度。基于經典的約束混凝土受壓本構模型，相關學者[17-20]針對尺寸效應、混凝土強度、截面形狀、縱向鋼筋布設、FRP種類等諸多影響因素開展了廣泛研究，從而得到了準確而精細化的約束混凝土受壓應力-應變模型。借鑒約束混凝土柱的研究思路，區別木材與混凝土的材料性能，可探索內嵌筋材外包FRP布加固木柱的軸心受壓應力-應變關系。

綜上所述，為了探究內嵌鋼筋外包CFRP布復合加固木柱的有效性和可靠性，同時提出復合加固木柱軸心受壓應力-應變模型，以指導該種方法的數值模擬和工程應用，本文共完成了42根復合加固短木柱的軸心受壓試驗。并依據試驗結果，參考約束混凝土柱相關理論，提出了復合加固木柱軸心受壓應力-應變模型。

1 試驗概況

1.1 試驗試件及材料性能

為了研究復合加固圓形木柱的強度和延性變化，探究其破壞機理、得到受壓應力-應變模型，試驗試件均采用受壓短柱。木柱的直徑為235 mm，高為800 mm，主要的試驗變量為內嵌鋼筋的數量以及外包CFRP布的形式。圖1所示為試件內嵌鋼筋的數量及其布設位置；圖2則為試驗中CFRP布的纏繞形式和位置；考慮試驗影響因素的具體試驗分組列于表1之中。

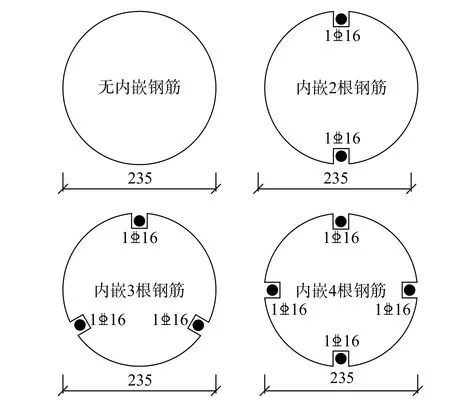
圖1 內嵌鋼筋數量及位置示意圖/mmFig.1 Number and location of mounted steel bars

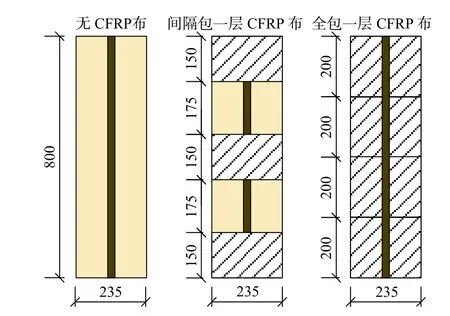
圖2 CFRP 布的布置形式/mmFig.2 Arrangement modes of CFRP strips

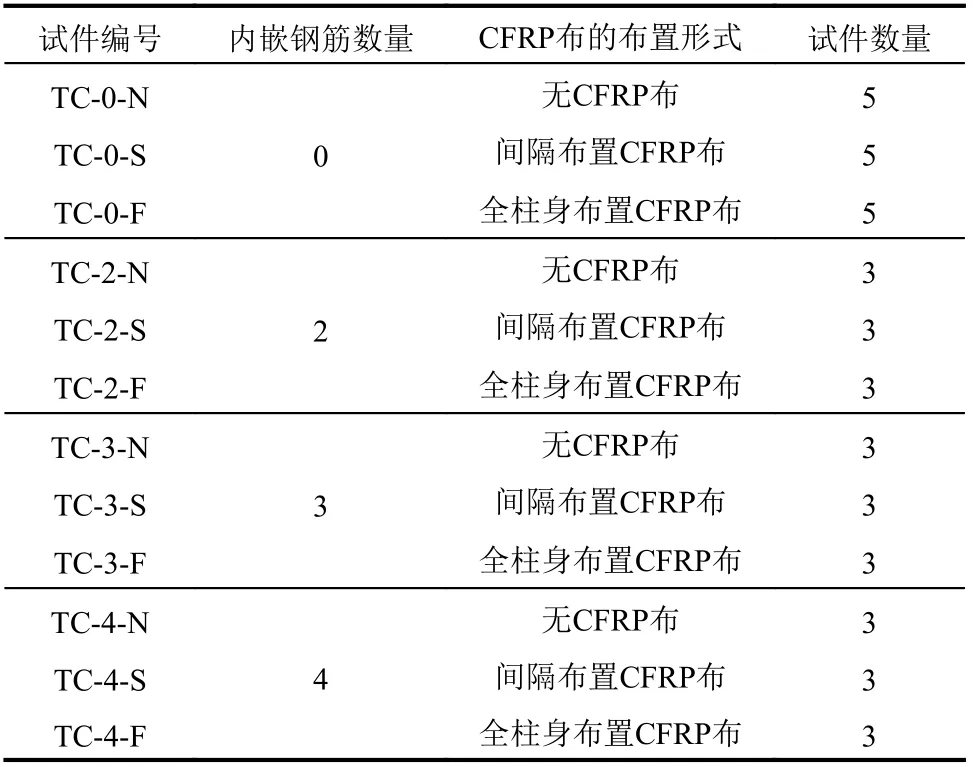
表1 試件分組Table 1 Specimen groups

試件制作的具體步驟為：依據既定的加固方案，在木柱表面開截面尺寸為24 mm×24 mm 的通長方槽；將直徑16 mm、長度800 mm 的鋼筋通過植筋膠黏結于木槽之中。待膠體硬化后，裁剪相應長度的CFRP布并用浸漬膠浸透；清潔木柱表面，將CFRP布纏繞于預定位置，搭接長度為120 mm。試件在室溫下養護7 d，便可進行軸心受壓試驗。

試驗中木材種類為花旗松，密度和含水率分別為0.56 g·cm-3和11.4%；木材的順紋抗壓強度為54.8 MPa，彈性模量為17440 MPa。木材的物理力學性能均通過無疵小試樣測定。內嵌筋材選用直徑16 mm 的HRB400級鋼筋，彈性模量為200 GPa；實測屈服強度為432 MPa，極限應變為0.134。試驗用CFRP布的厚度為0.167 mm，通過拉伸試驗測得其抗拉強度為3521 MPa，彈性模量為215 GPa，極限應變為0.016。

鋼筋與木材的黏結采用JGN805型雙組份環氧樹脂植筋膠，其劈裂抗拉強度和抗壓強度分別為11.5 MPa 和83.5 MPa；抗彎強度和抗剪強度分別為70.5 MPa 和16.1 MPa。CFRP布的粘貼采用與之配套的碳纖維浸漬膠，抗拉強度為53.2 MPa。

1.2 試驗裝置及數據量測

圖3為試驗裝置示意圖，豎向荷載由6000 kN電液伺服壓力試驗機施加。加載制度為：首先采用力控制加載，速率為1 kN/s；當試驗荷載達到500 kN 后轉變為位移控制加載，速率為0.5 mm/min；荷載下降至峰值的70%時，試驗停止。

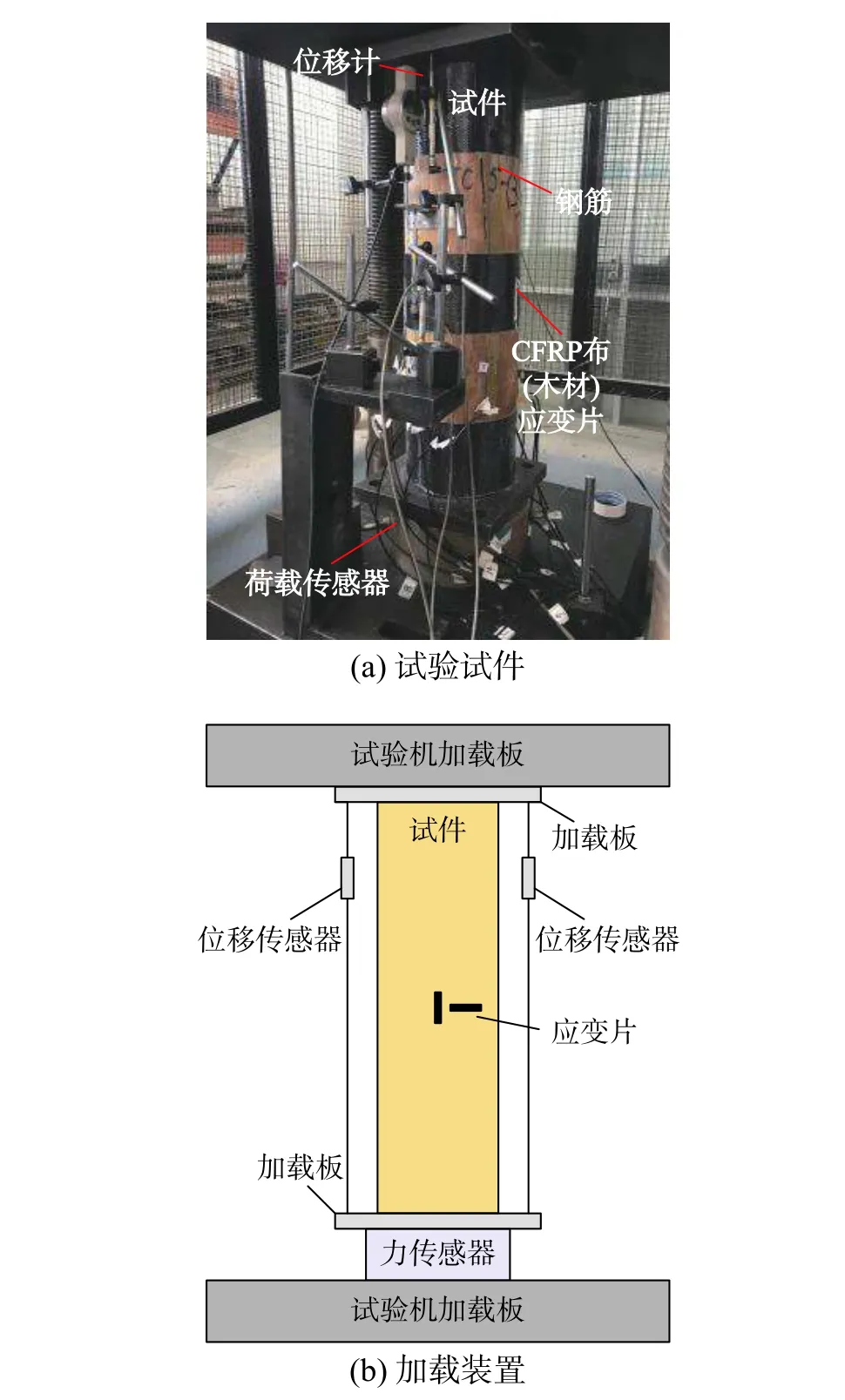
圖3 試驗裝置Fig.3 Test setup

試驗力由荷載傳感器獲取，木柱的軸向位移通過對稱布置的兩支位移傳感器采集。在木柱中部區段環向布置有橫、縱向應變片以量測加固木柱的變形信息。此外，CFRP布應變片與木柱的應變片布設位置一致；鋼筋縱向中心同樣布設有應變片以獲取其軸向變形。上述所有量測數據均由IMC動態測試系統同步采集獲取。

2 試驗結果

2.1 試件破壞形態

圖4列出了試驗中典型試件的破壞形態。圖4(a)為對比柱的破壞形態，圖4(b)為僅嵌筋加固木柱的破壞形態。加載初始階段，并無明顯試驗現象；當試驗荷載達到極限承載力后，初始缺陷集中區域的木材發生開裂、褶皺和外凸，內嵌鋼筋屈曲，進而木柱喪失承載力發生破壞。

圖4 試件破壞形態Fig.4 Failure modes of specimens

復合加固木柱(圖4(c)和圖4(d))由初始加載至達到峰值荷載，試驗現象并不顯著；隨著加載曲線進入下降段，木紋撕裂聲加劇且連續不間斷。木柱的破壞主要集中于具有初始缺陷(如木節、髓心、干縮裂縫等)的區域，隨著豎向荷載地持續施加，木節發生壓潰、干縮裂縫變寬且延伸。木節周邊區域的木纖維由于局部應力集中，發生壓潰、褶皺和外凸等現象。木材的橫向變形受到CFRP布的約束作用，當CFRP布達到其極限拉伸強度后發生脆性破壞，內嵌鋼筋失去CFRP布的約束作用進而發生屈曲破壞，上述約束作用地削弱加速了木柱的破壞。由于木材初始缺陷的存在，本文采用的復合加固方法雖然可以顯著提升木柱的承載和變形能力，但不能影響和改變木柱的破壞位置(如圖4(a)～圖4(d)所示)。

各組試件加固材料的破壞過程較為一致。CFRP布由于木材的顯著變形而產生局部的高度應力集中，達到其極限拉應變后，發生脆性斷裂。失去CFRP布的約束作用，隨著木柱豎向變形的累積，內嵌鋼筋隨即發生受壓屈曲。試驗中植筋膠往往發生劈裂破壞，或者與木材脫黏。

2.2 試件荷載-應變曲線

圖5對比了試驗中木材、CFRP布以及鋼筋的荷載-應變曲線，由于每組三個試件的應變曲線分布規律基本一致，因此圖中僅列出了每組一個試件的荷載-應變曲線。

圖5中橫坐標正向為各材料的橫向應變曲線，橫坐標負向為縱向應變曲線，應變數據通過木柱中部區域布設的應變片采集。試件接近峰值荷載時，多數應變片退出工作，故圖5中僅給出試件的荷載-應變上升段曲線。

由圖5可知，木材與CFRP布的橫向應變和縱向應變均具有良好的對應關系，表明木材與CFRP布之間具有可靠的黏結，因而CFRP布可以有效地約束木材的受壓變形。木材與其表面內嵌鋼筋的縱向應變分布曲線相近，表明二者可以協調變形、共同工作。木材、CFRP布以及內嵌鋼筋的協同變形，可以確保內嵌鋼筋、外包CFRP布復合加固古建木柱的有效性。

試件的荷載-應變曲線分布表明，隨著內嵌鋼筋數量以及CFRP布用量的增加，木柱的承載力隨之顯著提升。CFRP布可以有效約束內嵌鋼筋，防止其過早屈曲，從而改善了內嵌鋼筋的工作性能。而內嵌鋼筋的承壓作用可以減緩木材的橫向變形，使其在較大豎向荷載作用下受到CFRP布的約束作用，從而間接促進了CFRP布的加固效果。可知CFRP布與內嵌鋼筋的協同工作、相互促進作用可以進一步提升木柱的承載能力。

3 軸心抗壓強度計算

3.1 CFRP布有效約束應力

類比箍筋對核心混凝土的約束，CFRP布對于木柱的約束作用如圖6所示，對CFRP布建立力的平衡方程可得：

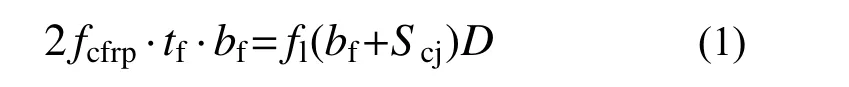
式中：fcfrp為CFRP布的拉伸應力；tf、bf為CFRP布的厚度和寬度；fl為CFRP布所施加的約束應力；Scj為CFRP 布的凈間距；D為木柱的直徑。

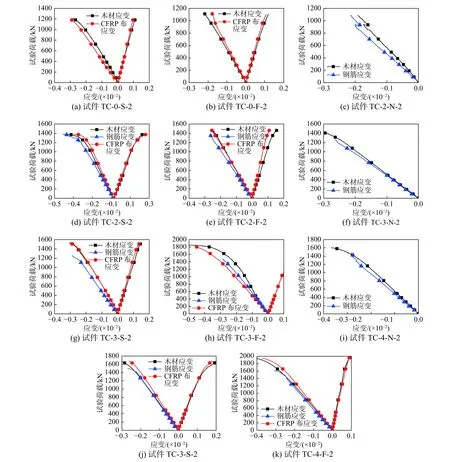
圖5 試件材料荷載-應變曲線Fig.5 Load-strain curvesof specimen materials

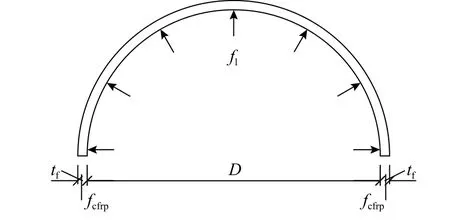
圖6 CFRP 布約束作用示意圖Fig.6 Lateral confinement of CFRPstrips

考慮到試驗中CFRP布間隔粘貼形式，類似于箍筋對核心混凝土的約束模式，因而在CFRP布的粘貼間隔區段存有無效約束區域。假定相鄰CFRP布之間為拱作用模式(圖7)，拱曲線為初始斜率45°的二次拋物線。可知，CFRP布粘貼區域其約束作用最強，有效約束區面積最大；CFRP布粘貼間隔的中心位置其約束作用最弱，有效約束區面積最小。取相鄰CFRP布粘貼間隔中心位置處截面為計算控制截面，其有效約束面積Acj可表示為：

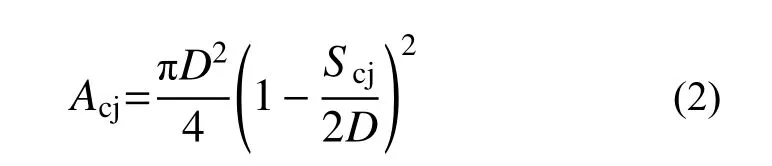
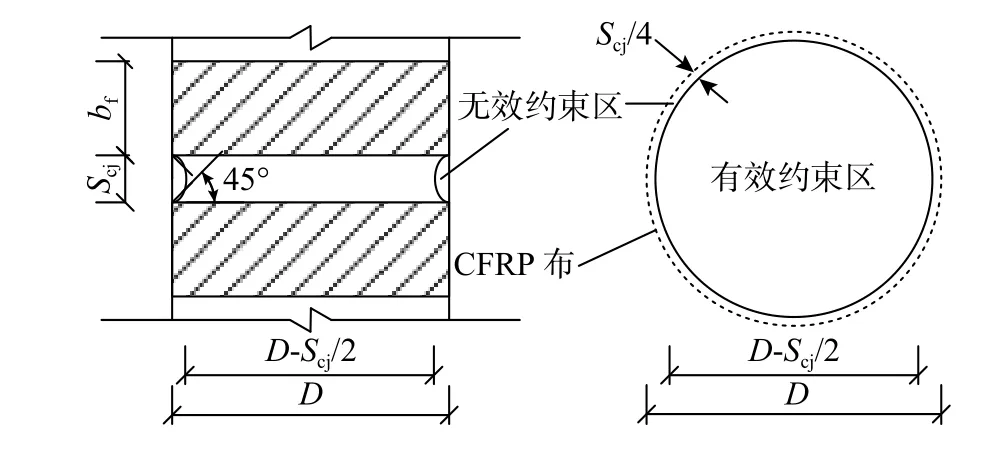
圖7 CFRP布有效約束區示意圖Fig.7 Effectiveconfinement section of CFRP strips

引入有效截面約束系數ks以考慮CFRP布的粘貼間隔對其約束作用的削弱：

式中，At為木柱截面面積。

依據CFRP布加固混凝土柱軸心受壓試驗與理論研究[14]可知，當加固試件達到峰值荷載時，CFRP布的張拉應力并未達到其極限強度。這種現象的產生可能是由于局部應力集中、CFRP布的纏繞工藝以及其實際受力狀態差別于材性試驗等。因而本文引入了CFRP布有效應變系數kε以計算試件峰值荷載時，CFRP布實際的張拉應力。目前缺乏對CFRP布約束木柱有效應變系數kε的研究[12]，采用試驗量測數據，應對不同內嵌鋼筋數量木柱試件，本文有效應變系數kε取值于0.10～0.27。

由CFRP布的受力平衡方程、有效截面約束系數ks以及有效應變系數kε可得CFRP布對于木柱的有效約束應力，其計算表達式為：

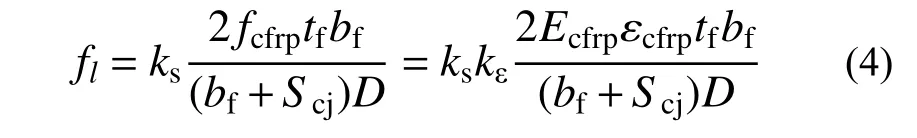
式中，Ecfrp、εcfrp分別為CFRP布的彈性模量和極限拉伸應變。

3.2 復合加固木柱峰值應力計算

參考相關研究，多數CFRP布約束混凝土抗壓強度模型是基于Richart 約束混凝土強度計算模型[21]修正后得到的，其表達式為：

式中：fcc為加固試件受壓峰值應力；fco為未加固試件抗壓強度；k1為CFRP布應力有效約束系數；fl為CFRP布的有效約束應力。

基于試驗數據和Richart 約束混凝土模型，以內嵌鋼筋試件抗壓強度為fco，以在內嵌鋼筋加固木柱基礎上粘貼CFRP布試件的受壓峰值應力為fcc，擬合得到了CFRP布有效約束系數k1，如圖8所示。木材是一種生物質建材，其材料離散性顯著，而且初始缺陷將加劇數據點的離散程度。因此有效約束系數k1的擬合決定系數R2相對較低，但是擬合結果對于加固木柱峰值應力的計算誤差在可接受范圍之內。將擬合結果代入式(5)，進而得到式(6)所示的復合加固木柱軸心受壓峰值應力計算模型。

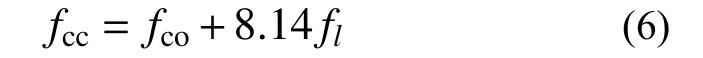
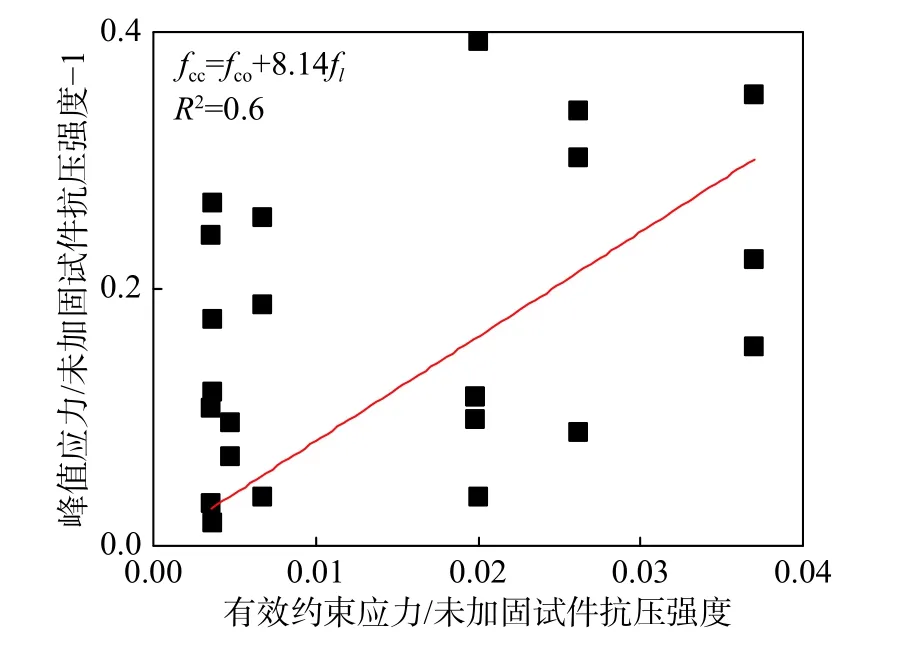
圖8 應力有效約束系數k1擬合Fig.8 Fitting of effective confinement coefficient k1

3.3 復合加固木柱峰值應變計算

根據CFRP布約束混凝土應力-應變關系的相關文獻可知[14]，試件峰值應變εcc與未加固試件峰值應變εco的比值(εcc/εco)與CFRP布的有效約束應力fl存在一定比例關系，如式(7)所示：

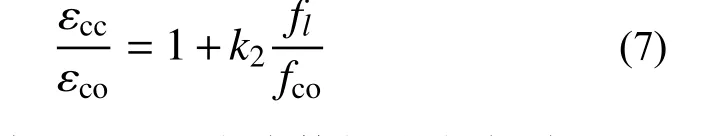
采用表達式(7)，對試驗數據進行擬合。以(fl/fco)為自變量，(εcc/εco-1)為因變量，所得CFRP布應變有效約束系數k2的擬合結果如圖9所示。不可避免的，應變有效約束系數k2同樣受到木材材料性能的離散性影響，但是其擬合結果對于峰值應變的計算具有可靠性。式(8)為復合加固木柱受壓峰值應變計算公式。

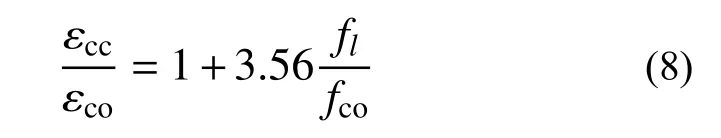
4 三折線型應力-應變模型

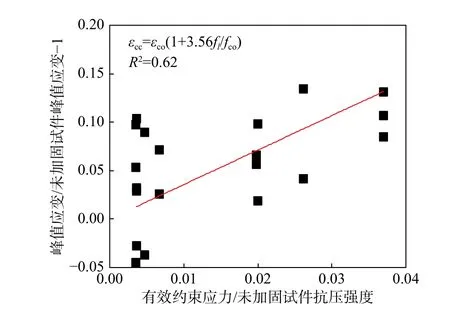
圖9 應變有效約束系數k2擬合Fig.9 Fitting of effective confinement coefficient k2

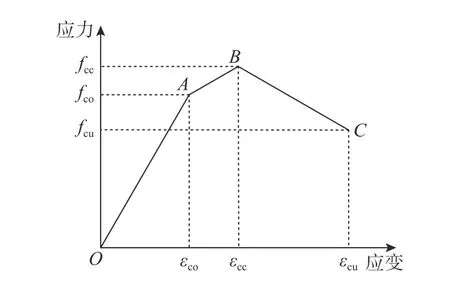
圖10 三折線應力-應變模型示意圖Fig.10 Schematic of trilinear stress-strain model

依據軸心受壓試驗得到的木柱荷載-軸向位移曲線以及荷載-軸向應變曲線，可推測復合加固木柱應力-應變曲線基本符合圖10所示的三線式分布特征。為得到復合加固木柱軸心受壓應力-應變模型，只需確定圖10中的三個特征點A、B和C。特征點A對應僅內嵌鋼筋試件的峰值應力以及其所對應的應變；特征點B為曲線上升段與軟化段的拐點，可采用復合加固試件的峰值應力和峰值應變確定其坐標；特征點C為軟化段的終點，代表復合加固試件的極限應力和極限應變，取0.85fcc以及其所對應的應變作為該點的計算數值。

4.1 第一段曲線方程

加載初期曲線斜率應為僅內嵌鋼筋加固木柱的受壓彈性模量，但是通過試驗試件的荷載-應變曲線分布可以看出，從初始加載階段CFRP布便對木柱提供約束作用。因此，為了充分考慮CFRP布對于加固木柱的約束效應，本文采用Mander等[22]建議的受橫向約束試件初始彈性模量與其峰值抗壓強度的關系表達式，以確定OA段曲線的斜率：

基于初始彈性模量與峰值應力關系式(9)，對試驗數據進行回歸分析，以試驗試件的峰值應力fcc為自變量，試驗所得上升段曲線斜率E0為因變量，對斜率相關系數α 進行擬合。圖11為具體擬合曲線，最終得到了三折線型應力-應變模型中第一段曲線OA的斜率計算表達式，如式(10)所示。

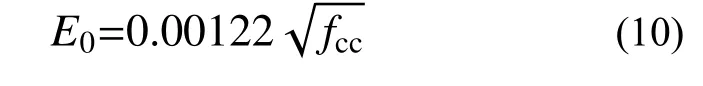
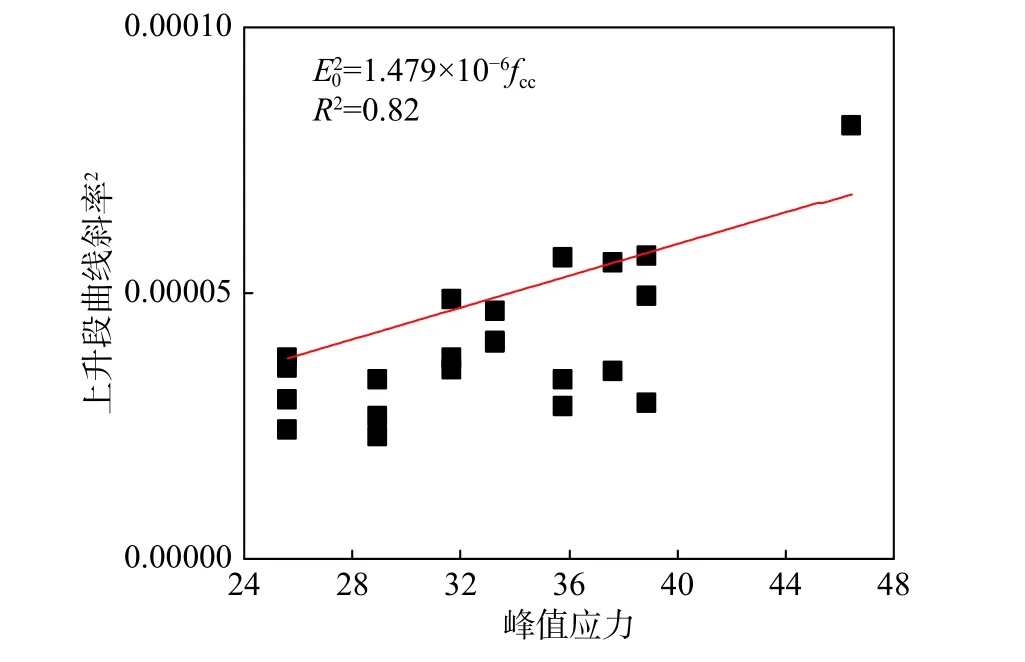
圖11 斜率相關系數α 擬合結果Fig.11 Fitting result of coefficient α

得到OA段曲線斜率后，可確定三折線型應力-應變模型中的第一段曲線方程為：

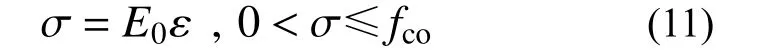
4.2 第二段曲線方程

圖10中曲線AB段表現為CFRP布對木柱抗壓強度的約束增強作用。由本文第3節中提出的式(6)和式(8)可計算出B點的縱、橫坐標；由式(10)和式(11)可確定A點的坐標。從而可以得到AB段曲線方程，即三折線型應力-應變關系中第二段曲線方程，見表達式(12)和式(13)。

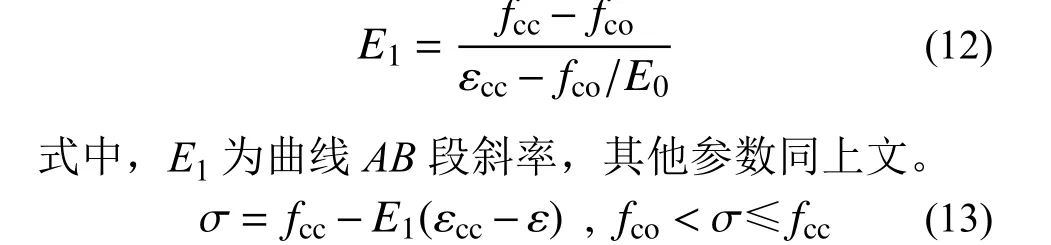
4.3 第三段曲線方程

由于CFRP布的水平約束作用有限，應力-應變曲線在過峰值后進入軟化階段。受木材初始缺陷的影響，復合加固木柱受壓應力-應變曲線下降段離散性較大。因此本文選取軟化段曲線中，應力數值為0.85fcc的點作為應力-應變曲線的終點。根據試驗數據，在確定C點的坐標后，聯合已知的B點坐標，便可對曲線BC段的斜率E2進行擬合。考慮到曲線軟化段斜率依然與CFRP布的約束應力存在比例關系，軟化段斜率與CFRP布有效約束應力關系表達式如下：

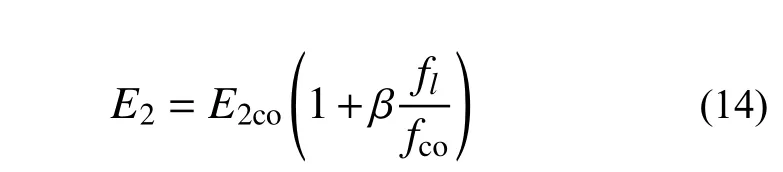
式中：E2co為僅嵌筋加固試件軟化段斜率；β 為斜率相關系數。

依據式(14)，采用相關試驗數據，對斜率相關系數β 進行擬合，擬合曲線如圖12所示；進而得到了受壓應力-應變關系第三段曲線BC的斜率計算式(15)。由試驗研究可知，復合加固木柱下降段曲線受木材初始缺陷影響顯著，數據點的分布具有一定的離散性。雖然斜率相關系數的擬合決定系數R2相對較低，但擬合結果可以反映軟化段曲線的分布特征。通過B點坐標，以及曲線BC段斜率，可確定應力-應變關系第三段曲線方程，即式(16)。

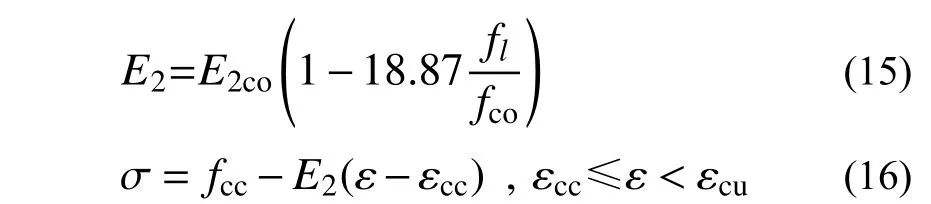
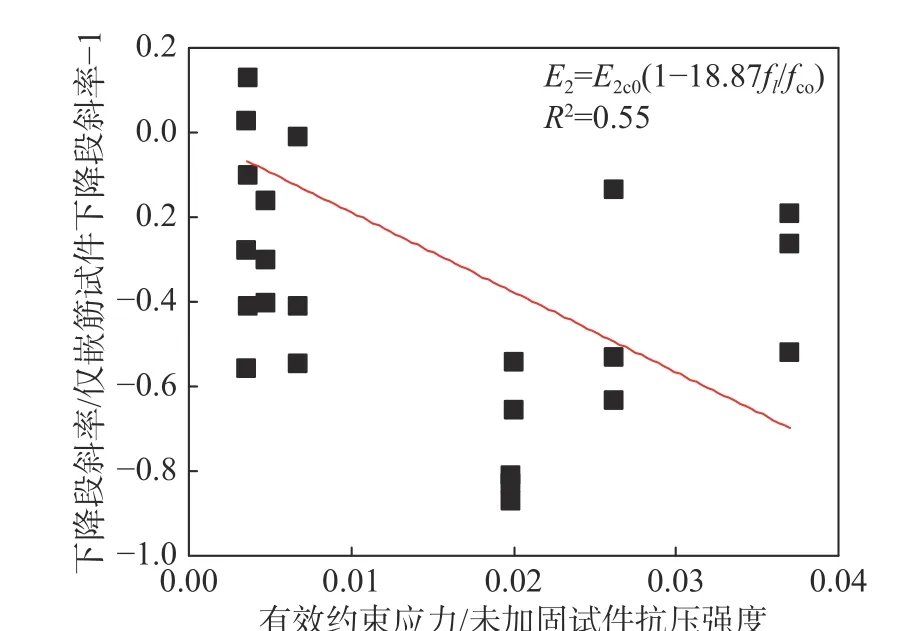
圖12 斜率相關系數β 擬合結果Fig.12 Fitting result of coefficient β

綜合上述三折線型應力-應變關系各分段曲線的表達式，最終得到了式(17)所示的復合加固木柱軸心受壓應力-應變曲線方程。

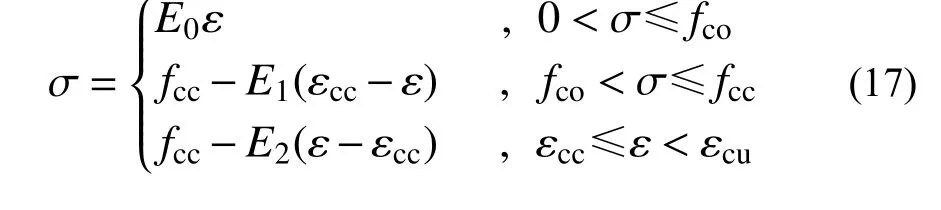
5 多項式型應力-應變模型

本文第4節中提出的復合加固木柱三折線型應力-應變模型形式簡單，同時能夠較為準確的反映加固木柱的受力特性。但是考慮到其三折線的形式，存在的曲線拐點使其與實際的木柱受壓應力-應變曲線存有差別。依據Youssef 等[23]提出的FRP布約束混凝土柱的計算模型，可將三折線模型中的兩段上升曲線轉變為一條多項式曲線，進而得到復合加固木柱多項式型的應力-應變模型。

假設加固木柱應力-應變上升段(0＜ε＜εcc)曲線方程為多項式形式，表達式為：

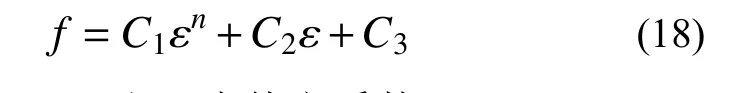
式中：C1、C2、C3和n為待定系數。

式(18)中的系數需要通過曲線的邊界條件來確定，如式(19)所示。

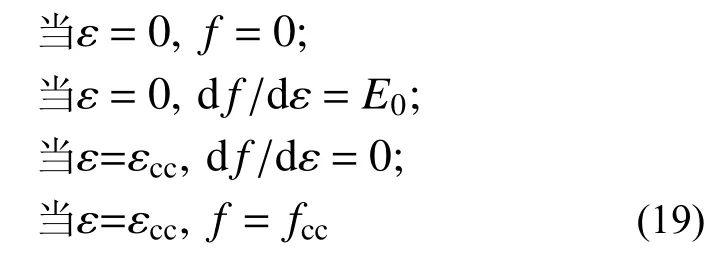
式(20)和式(21)為由式(18)和式(19)聯合求解得到的復合加固木柱應力-應變模型上升段方程。多項式型應力-應變模型下降段曲線的求解與三折線型應力-應變模型一致，具體如式(16)所示。綜合上升段曲線方程以及軟化段解析式，可以確定復合加固木柱軸心受壓多項式型應力-應變模型。

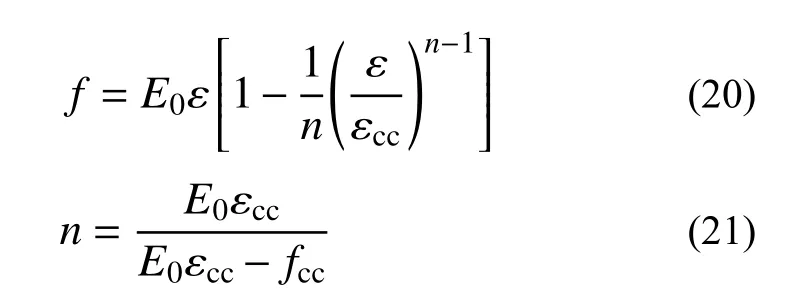
6 模型曲線與試驗曲線的對比

通過對試驗數據的擬合分析，本文最終得到了三折線型和多項式型的復合加固木柱軸心受壓應力-應變模型。為了驗證所得本構模型的可靠性，將模型計算曲線與試驗曲線對比于圖13。

由圖13可知，充分考慮木材作為生物質建材具有的顯著離散性，三折線型和多項式型應力-應變模型上升段曲線和峰值應力計算均與試驗曲線基本吻合。對比應力水平由峰值下降至85%的軟化段曲線，模型曲線斜率與試驗曲線斜率相近。多項式型與三折線型應力-應變模型曲線分布趨勢基本一致，三折線型模型曲線存在有拐點，而多項式型模型曲線分布則更為光滑。

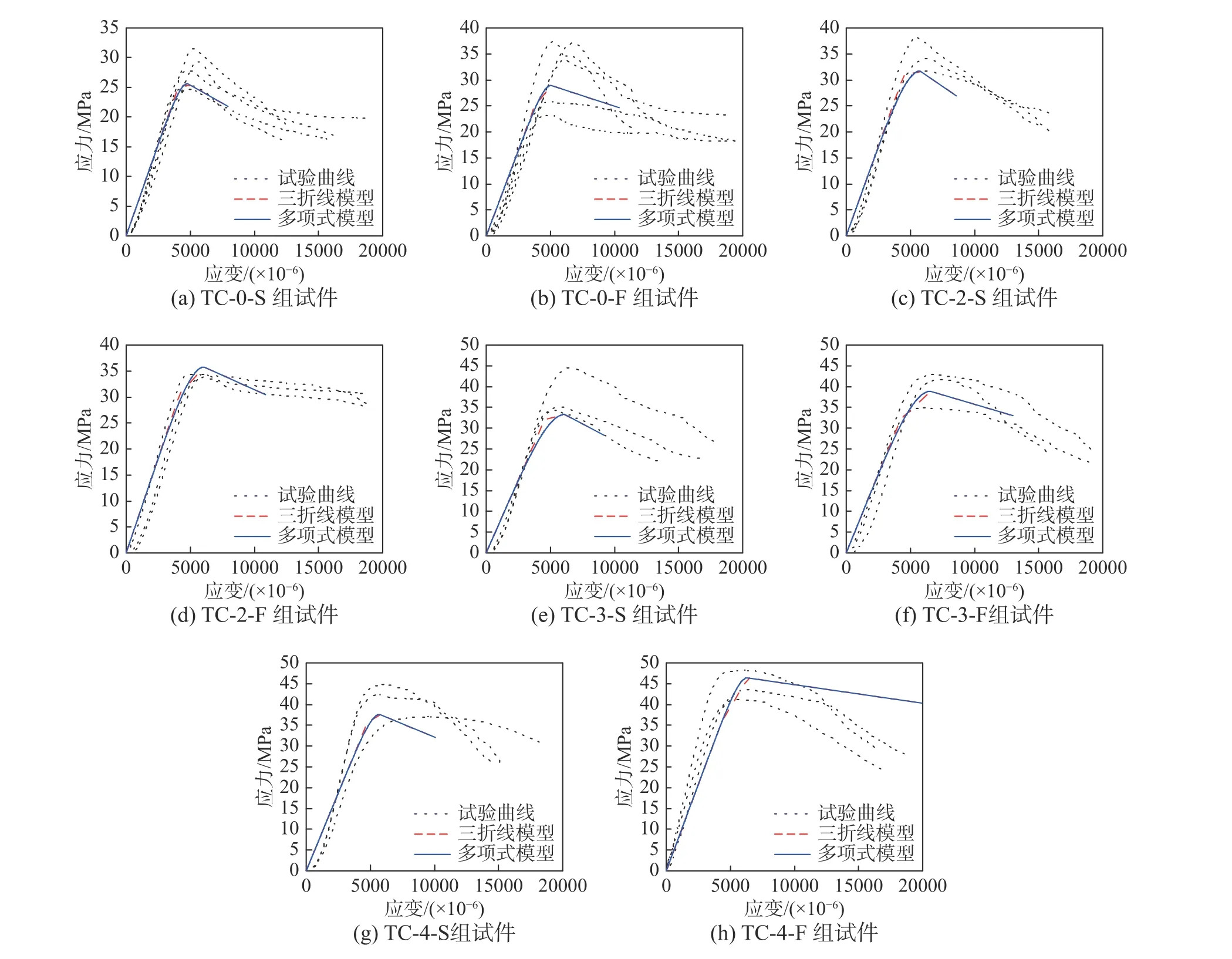
圖13 理論模型與試驗曲線對比Fig.13 Comparison between theoretical model and experimental curves

依據圖13中各加固工況下試件的應力-應變模型可知，CFRP布用量以及內嵌鋼筋數量均顯著影響模型曲線的分布規律。當內嵌鋼筋數量相同時，隨著CFRP布用量的增加，木柱的峰值應力提升明顯且曲線軟化段斜率減小。當CFRP布的加固量一定時，隨著內嵌鋼筋數量的增加，加固木柱的峰值應力提升而曲線軟化段斜率變化不顯著。但是當CFRP布沿全柱身布置時，隨著內嵌鋼筋數量的增加，曲線的位移延性得到提升。表明在CFRP布有效約束作用下，內嵌鋼筋能夠提升木柱的變形能力。

當木柱內嵌鋼筋數量較多時，模型曲線與試驗曲線軟化段分布有所差別(如圖13(g)和圖13(h))。這是因為當內嵌鋼筋數量較多時，在CFRP布的有效約束作用下，試件的峰值應力得到提升。過峰值后，試件仍處于較高的應力水平，木柱的破壞可能發生在多個不確定的薄弱區域。因而同一組試件的軟化段曲線存在離散性，進而所得模型曲線與試驗曲線產生差異。

7 結論

通過42根內嵌鋼筋外包CFRP布復合加固短木柱的軸心受壓試驗以及數據擬合分析，本文提出了三折線型和多項式型兩種復合加固木柱的軸心受壓應力-應變模型。論文研究結論如下：

(1)內嵌鋼筋外包CFRP布復合加固方法可以有效提升木柱的承載力同時能夠改善其延性；由于木材不可避免的存在有初始缺陷，盡管采用復合加固方法，木柱的破壞依然發生于初始缺陷較為集中的區域。

(2)木材、CFRP布和鋼筋的荷載-應變曲線對應良好，表明三種材料可以協調變形、共同工作；鋼筋的承壓作用以及CFRP布的約束作用可以相互促進，共同提升木柱的受壓承載能力。

(3)參照CFRP布約束混凝土柱的相關研究，提出了復合加固木柱軸心受壓峰值應力以及其所對應的峰值應變計算公式。

(4)通過對試驗數據的擬合分析，確定了模型曲線中關鍵點的坐標，得到了各段曲線的方程表達式；進而給出了三折線型和多項式型復合加固木柱軸心受壓應力-應變模型。

(5)所得三折線型和多項式型復合加固木柱應力-應變曲線與試驗曲線基本吻合，且模型曲線分布受到CFRP布用量和內嵌鋼筋數量的影響。