翅片管冷凝器低壓環境下空氣側換熱特性研究

張汝行 柳建華,2 張 良

(1 上海理工大學能源與動力工程學院 上海 200093； 2 上海市動力工程多相流動與傳熱重點實驗室 上海 200093)

翅片管冷凝器作為熱泵系統的空氣處理設備和高效換熱裝置，一直都是研究人員研發和改進的熱點。1971年，F. C. McQuistion等[1]率先提出了平翅片換熱器空氣側換熱模型，其傳熱因子的預測偏差達34.4%。隨后， Wang C. C.等[2-3]通過研究翅片管換熱特性提出了被廣泛認可的傳熱因子關聯式。W. Pirompugd等[4]利用有限環肋法全面地分析了各種工況下的翅片換熱，并建立了濕工況的傳熱傳質關聯式。Ma Xiaokui等[5]研究發現濕工況下傳熱因子和傳質因子隨著翅片間距的增加而增大。N. H. Kim等[6]研究發現條縫翅片的摩擦因子大于平翅片的摩擦因子，且增幅隨管排數的增加而變大。鞠培玲等[7]研究了翅片管換熱器在析濕工況下的積灰特性及積灰對空氣側壓降的影響，結果表明翅片表面的析濕量決定積灰程度，積灰程度與摩擦壓降成正比。最近，谷波等[8]研究了兩種不同類型的光滑波紋翅片的空氣側性能，并對已有實驗關聯式進行了修正。隨著高原地區的發展以及浮空平臺技術的應用，熱泵開始逐漸應用于低壓工況中。在常壓環境下，翅片管冷凝器的空氣側熱阻遠大于管內側，是強化換熱的主攻方向。但低壓下空氣的密度較低，表征對流換熱的空氣側雷諾數減小，可知翅片管冷凝器的對流換熱表面傳熱系數較常壓下有明顯區別。胡松濤等[9]測試了電加熱器在常壓和低壓環境下的表面傳熱系數和散熱功率，認為電加熱器表面傳熱系數與環境氣壓的0.2次冪成正比。林暉等[10]利用G-M低溫制冷機，測量和分析了低溫低壓條件下水平圓管自然對流換熱特性，并給出了無量綱實驗準則式。王晶等[11]研究了豎直平板在不同環境壓力(0.001～101 kPa)和加熱量(75、150、300 W/m2)下的散熱，結果表明對流換熱表面傳熱系數在絕對氣壓小于1 kPa時非常小，可視為0；在絕對氣壓大于1 kPa時，對流換熱表面傳熱系數隨壓力的升高呈2次冪增加。劉旗等[12]對低壓濕工況下的蒸發器進行研究，研究了劉易斯因子的變化規律和影響因素，并引入了壓力修正因子。張嘉文等[13-14]總結了目前具有較高認可度的空氣側理論換熱模型，并根據低壓下蒸發器換熱特性對模型進行了修正。

現階段有關低壓下翅片管換熱器的少量研究主要針對蒸發器，空氣側屬于冷卻過程且過程中伴隨著析濕傳質，而冷凝器則是完全的顯熱交換。在Dittus-Boelter[15]的強制對流關聯式中，加熱流體與冷卻流體存在明顯的不同。

目前，有關翅片管式冷凝器在低壓環境下通過空氣散熱的研究非常少。本文搭建了一個翅片管冷凝器在低壓下的換熱實驗臺，研究低壓環境對翅片管換熱器空氣側對流換熱的影響，同時驗證現有常壓下翅片管換熱模型在低壓條件下的適用性。

1 實驗系統

低壓換熱實驗系統如圖1所示。實驗系統由翅片管冷凝器、環境倉、電加熱、加濕器、循環風機、真空泵、溫濕度傳感器、壓力傳感器、采集儀組成。為提高耐壓強度及密封性，環境倉采用不銹鋼材料構成封閉環形。環境倉包括循環段與測試段：循環段為DN350的圓形通道，測試段為500 mm×500 mm的矩形通道。電加熱器和真空泵能根據實驗要求調節換熱器入口空氣的溫度以及環境倉壓力。在測試段入口前布置均流板，以確保測試段的氣流均勻性。在翅片管冷凝器的進出口處裝有溫濕度傳感器，在環境艙內布置多個壓力傳感器，用于檢測環境倉內各點的狀態參數。采用變頻軸流風機調節空氣循環量，并使用微壓差傳感器測量噴嘴前后壓差，根據噴嘴的前后壓差測量空氣的循環量。測試系統主要包括實驗參數的數據采集和運行工況的參數控制。實驗通過AGILENT采集儀與LabVIEW軟件實現數據參數的采集與顯示。

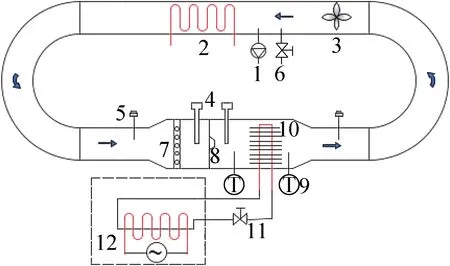
1真空泵；2電加熱器；3循環風機；4微壓差傳感器；5壓力傳感器；6調節閥；7均流板；8標準噴嘴；9溫濕度傳感器；10翅片管冷凝器；11流量調節閥；12熱水循環系統。

翅片管冷凝器采用三角形錯列排列方式，具體翅片管參數和結構如表1和圖2所示。由于制冷劑的冷凝溫度較難控制，實驗中利用40～50 ℃的熱水作為管內的換熱工質。循環熱水的進出溫度由兩個Pt100溫度傳感器測得，其校準精度為0.1 ℃。循環熱水的體積流量由渦輪轉子流量傳感器測得，熱水溫度通過PID控制器調節。在實驗操作中，數據的穩定性判斷參考ASHRAE 41.2-2018標準[16]，即空氣側與水側的熱平衡偏差應小于5%。實驗工況：風速為1～4 m/s，環境壓力為40～101 kPa，縱向管排數為2～4排，入口水溫為40～50 ℃。

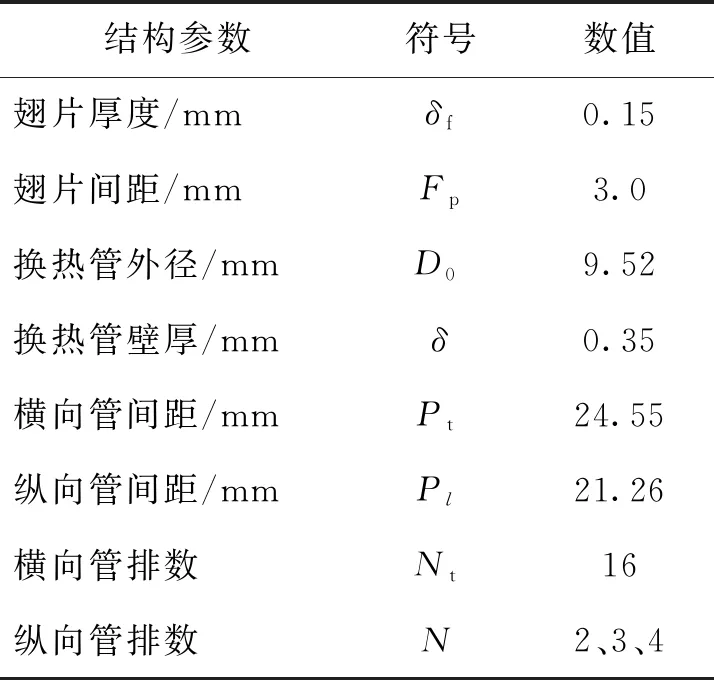
表1 翅片管冷凝器結構參數

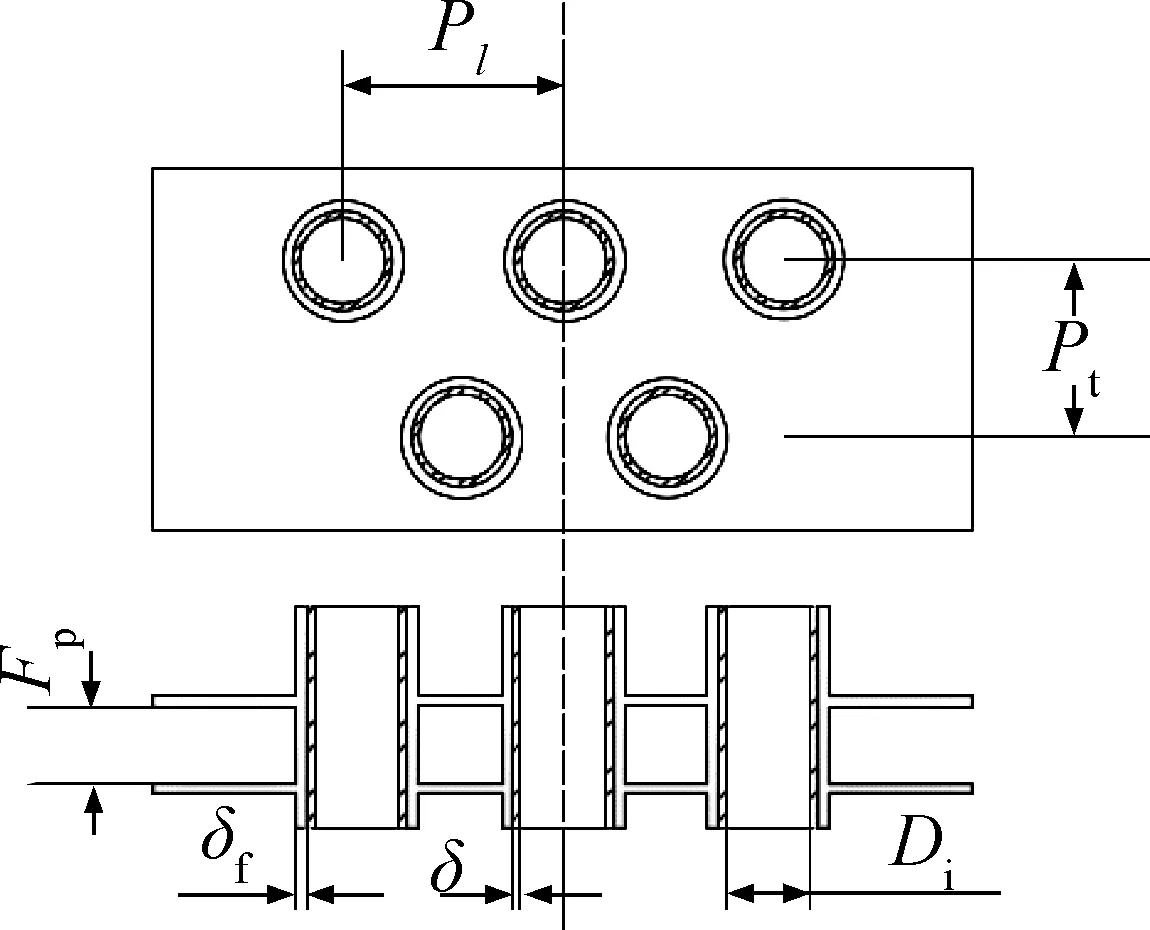
圖2 翅片管冷凝器的結構

實驗前首先進行常壓下換熱實驗，將常壓下的實驗數據與換熱模型[17]進行對比，結果表明最大相對偏差為28.4%，最小相對偏差為9.3%。這表明該實驗系統的設置合理、可靠性較高。

2 數據處理

2.1 傳熱計算

傳熱量Qair：

Qair=cpmair(tout,air-tin,air)

(1)

Qair=KAΔtm

(2)

對數平均溫差Δtm：

(3)

式中：cp為空氣的定壓比熱容，kJ/(kg·K)；mair為空氣的質量流量，kg/s；tin,air、tout,air分別為冷凝器的進、出口空氣溫度，℃；tin,w、tout,w分別為熱水的進、出口溫度，℃；A為管外總表面積，m2。

冷凝器的傳熱系數K：

(4)

式中：λt為紫銅管導熱系數，W/(m·K)；Ab為肋片間管外總表面積，m2；Ai為管內總表面積，m2；hw、hair分別為管內側水、管外側空氣的對流換熱表面傳熱系數，kW/(m2·K)；ηf為翅片效率；δ為管壁厚度，m。

管內熱水的物性溫度為進出口的平均溫度，流速根據質量流量計測得。利用Dittus-Boelter[15]公式或Gnielinski[18]公式計算管內循環熱水的對流換熱表面傳熱系數hw：

Dittus-Boelter[15]公式：

(5)

Gnielinski[18]公式：

(6)

fR為摩擦因子，采用下式計算：

fR=(1.58lnRew-3.28)-2

(7)

翅片效率：

(8)

(9)

(10)

式中：r0為管外半徑，m；R0為等效半徑，m；Rew為水側雷諾數；Prw為水的普朗特數；λw為水的導熱系數，W/(m·K)；Di為管內直徑，m；φ、M為翅片效率的計算參數；δf為翅片厚度，m；λf為翅片的導熱系數，W/(m·K)；ifg為飽和水的氣液潛熱，kJ/kg。

等效半徑R0：

R0=1.28W(L/W-0.2)1/2

(11)

式中：L為翅片長度，m；W為翅片寬度，m。

利用上式對各參數進行計算，最后代入式(2)中得到對流換熱表面傳熱系數hair。

2.2 實驗的不確定度分析

由于測量儀器存在精度等級，實驗過程中也會存在系統誤差。為提高實驗數據的可信度，利用Moffat[19]法對重要數據進行不確定分析。

Moffat[19]的不確定度計算方法：

假設影響U的一系列參數有：

U=U(X1,X2,X3,……Xn)

(12)

則U的合成不確定度為：

(13)

經計算，本實驗數據的不確定度如表2所示。

表2 實驗不確定度

3 數據分析

圖3所示為實驗測得的不同環境壓力和最窄面空氣側雷諾數Reair下對流換熱表面傳熱系數的變化，翅片管換熱器入口空氣的干球溫度為25 ℃，翅片管換熱器的熱水入口溫度為45 ℃，管排數為2。隨著Reair的降低，對流換熱必然降低。由圖3可知，在最窄面Reair為400～800的范圍內，隨著環境壓力的降低，對流換熱表面傳熱系數曲線的斜率明顯減小。說明在低壓環境下Reair與對流換熱的關系式發生改變。當Reair=400時，環境壓力從101 kPa降至40 kPa，對流換熱表面傳熱系數降低了44.1%。即在相同的Reair下，隨著環境壓力的降低，空氣側的對流換熱明顯減弱。由此可推斷環境壓力的降低抑制了空氣側擾動對換熱的強化。原因分析如下：在翅片結構未發生改變的情況下，雖然雷諾數具體值相同，但環境壓力的降低導致空氣密度降低，單位體積內空氣質量的減小必然會減小空氣中的各分子與加熱壁面的有效接觸次數，因此空氣側的對流換熱表面傳熱系數減小。

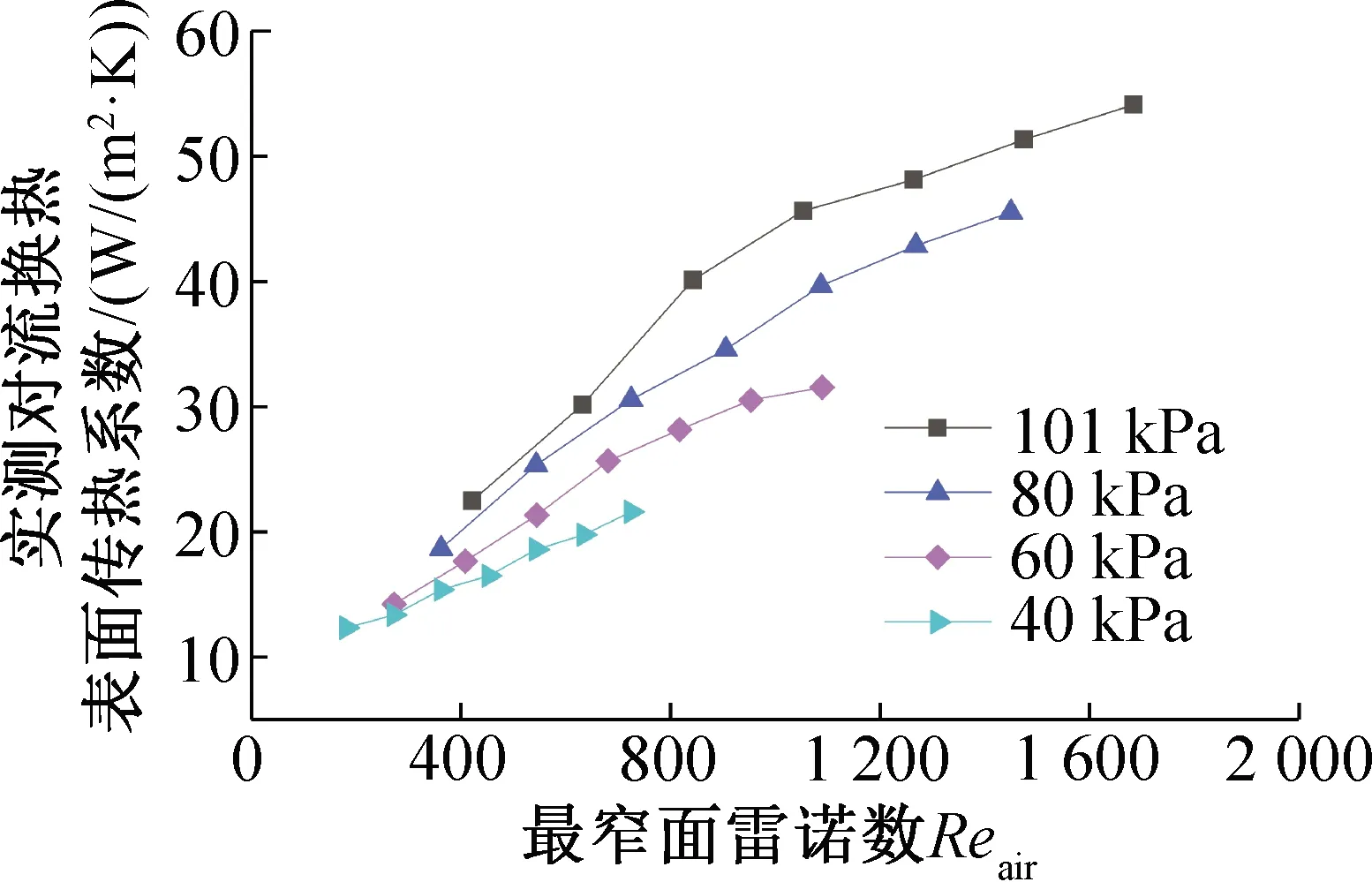
圖3 不同環境壓力和最窄面空氣側雷諾數時對流換熱表面傳熱系數的變化

圖4所示為管排數為2排，空氣流速為2.5 m/s時，不同環境壓力和加熱溫度下空氣側對流換熱表面傳熱系數的變化。由圖4可知，在40～101 kPa環境壓力中，當循環熱水入口溫度從40 ℃升至50 ℃，空氣側的對流換熱沒有發生明顯的規律性變化，表明對流換熱與管內外工質的流動參數、換熱面的結構有關，與溫差的大小無關。這與常壓條件下循環熱水溫度不會影響換熱的結論是一致的。

圖5所示為不同環境壓力下管排數對對流換熱的影響。隨著縱向管排數的增加，空氣側的摩擦阻力增加，導致空氣的擾動程度降低，造成對流換熱略有減小。此外，隨著環境壓力的降低，管排數對對流換熱的影響逐漸變弱。由此推斷低壓環境會削弱翅片結構對空氣側對流換熱的影響。原因是隨著環境壓力的降低，Reair開始減小，黏性力的作用開始增強，對流換熱變弱，因而宏觀層次上翅片結構對換熱的影響得到削弱。

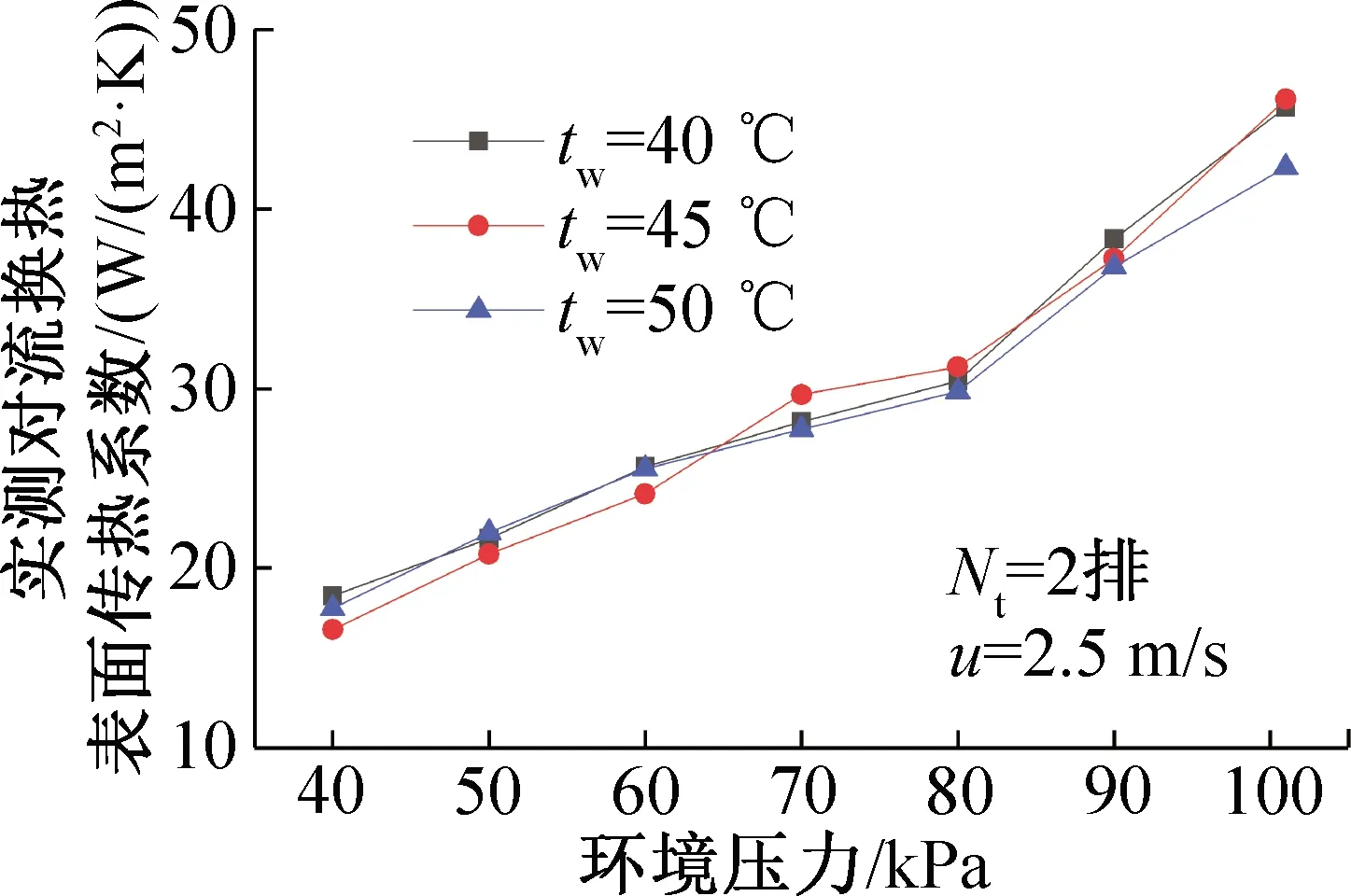
圖4 不同環境壓力和熱水溫度時對流換熱表面傳熱系數的變化

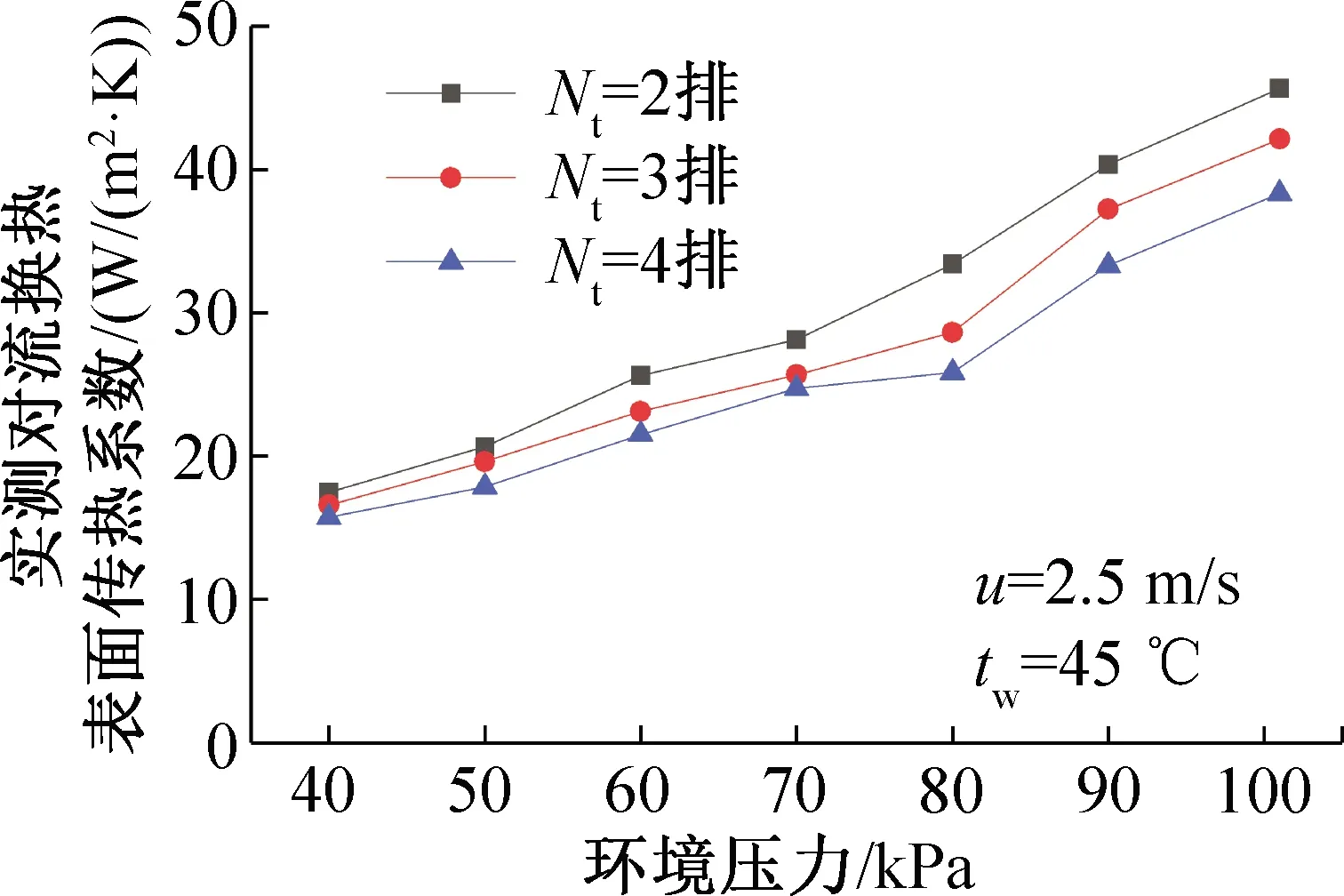
圖5 不同環境壓力和管排數時對流換熱表面傳熱系數的變化

將實測的對流換熱表面傳熱系數與常壓換熱模型[17]的計算結果進行對比，結果如圖6所示。隨著環境壓力的降低，實測對流換熱表面傳熱系數明顯小于常壓換熱模型[17]的計算結果，而且壓力越低偏移越大，當環境壓力從101 kPa降至40 kPa時，平均偏差從17.3%增至77.5%。

常壓下的對流換熱表面傳熱系數計算模型[17]：

(14)

m=-0.28+0.08Reair/1 000

(15)

n=0.45+0.006 6L/deq

(16)

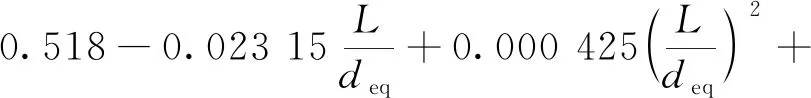
(17)

c=A(1.36-0.24Reair/1 000)

(18)

式中：λair為空氣導熱系數，W/(m·K)；L為翅片片寬，m；deq為當量直徑，m；Reair為最窄面的空氣側雷諾數。

由式(14)可知，當環境壓力改變時，主要變量是空氣側雷諾數，較大的偏差也證明隨著環境壓力的降低，雷諾數對空氣側對流換熱的影響變弱。

針對現有預測模型的局限性，根據不同環境壓力和縱向管排數下的實測對流換熱表面傳熱系數，對常壓換熱模型[17]進行修正，并且得到了適用于40～90 kPa壓力范圍內的修正因子B，如式(19)～式(20)，其R2=0.995，修正模型的對流換熱表面傳熱系數與實測對流換熱表面傳熱系數的對比如圖7所示，兩者的平均絕對偏差為9.5%。

(19)

(20)

式中：pl為低壓環境壓力，kPa；pa為標準大氣壓力，kPa，Nt為橫向管排數。

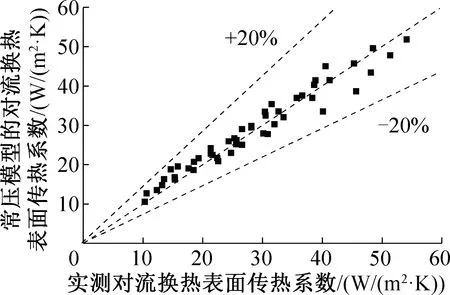
圖7 對流換熱表面傳熱系數的修正

4 結論

本文研究了低壓環境下平翅片管冷凝器的空氣側換熱特性，分析了低壓環境下空氣側雷諾數、管排數及加熱溫度與空氣側對流換熱的關系，得到如下結論：

1)在相同的空氣側雷諾數下，隨著環境壓力的降低，空氣側的對流換熱明顯減弱。在空氣側雷諾數為400時，環境壓力從101 kPa降至40 kPa，對流換熱表面傳熱系數降低了44.1%。

2)低壓環境下，增加管排數會降低對流換熱，這也與常壓下的空氣側換熱特性相同，但隨著環境壓力的降低，管排數對對流換熱的影響也會變弱。從實驗結果來看，改變循環熱水溫度沒有對低壓下的空氣側換熱產生明顯影響。

3)隨著環境壓力的降低，實測對流換熱表面傳熱系數開始小于常壓模型的計算結果。當環境壓力從101 kPa降至40 kPa，平均偏差從17.3%增至77.5%。針對現有預測模型的局限性，結合環境壓力、管排數對空氣側對流換熱的影響，對常壓模型進行修正，修正后的平均絕對偏差為9.5%。