例談數學分析中的有限與無限
李有連
(呂梁學院 離石師范分校,山西 呂梁 033000)
我們都知道數學分析這門課程就是用極限思想來研究函數的一門學科,而極限思想揭示了無限與有限的對立統一關系。借助極限思想,我們可以從有限認識無限,然后以無限為基礎得到相應的結果。
一、有限與無限的區別
數學分析中,有許多命題或定理只有在 “有限”時成立,在 “無限”時不再成立。
(一)加法結合律
在“有限”的情況下,加法結合律成立,但在“無限”的情況下就不再成立。
例如:?a,b,c都有(a+b)+c=a+(b+c)
按照有限的計算法則,假如數的加法可以任意結合,則有:
1+(-1)+1+(-1)+1+(-1)+…=[1+(-1)]+[1+(-1)]+[1+(-1)]+…=0
1+(-1)+1+(-1)+1+(-1)+…=1+[(-1)+1]+[(-1)+1]+[(-1)+1]+…=1
即出現了0=1,就有大問題了。所以說,有限到無限是引起 “質變”的。
(二)極限的四則運算法則
在“有限”的情況下,極限的四則運算法則成立,但在“無限”的情況下就不再成立。
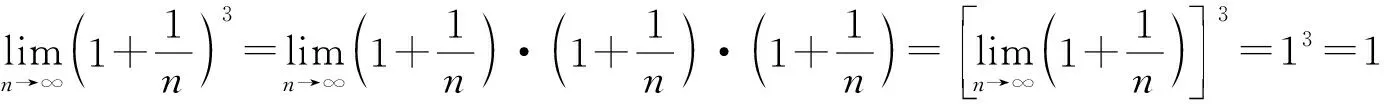
按照有限的計算法則:
再例如:有限個無窮小的和是無窮小,但無限個無窮小的和就不一定是無窮小。
(三)連續函數的四則運算法則
在“有限”的情況下,連續函數的四則運算法則成立,即有限個函數都在點x0處連續,那么其和在點x0處也連續,但在“無限”的情況下就不再成立。
例如:研究函數項級數∑un(x)=u1(x)+u2(x)+…+un(x)+…的和函數在其收斂域內的連續性,其中u1(x)=x,un(x)=xn-xn-1,n=2,3,…
解:顯然sn(x)=x+(x2-x)+…+(xn-xn-1)=xn

所以和函數s(x)在區間(-1,1)內連續,但在點x=1處不連續。
從這個例子可以看出,雖然級數的每一項在點x=1處不但連續,而且可導;但其和函數在點x=1處卻不連續,更談不上可導了。
二、有限與無限的聯系
在數學分析中“有限”與“無限”間建立聯系的手段,往往很重要。
(一)無限由有限構成

(二)有限由無限組成
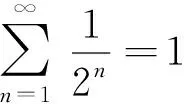
(三)有限轉化成無限
在初等數學研究中,我們習慣于把有限的任一初等函數轉化成無窮級數。

(四)無限轉化成有限
在數學中我們一般通過有限項之和的極限來定義無限項之和,這就是將無限轉化為有限。
例如:要證
對于一切自然數都成立的話,就必須采用數學歸納法。數學歸納法的運用就是把無限步的推理過程轉化為有限步,從而得到結果。在數學分析中計算數項級數的和也是同樣的道理。


所以級數的n項部分和
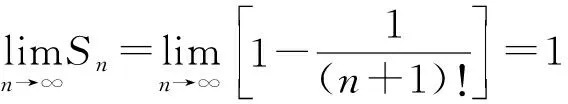
故級數的和為1。
總之,有限和無限是一對很有特色的數學概念。兩者相互交叉,相互聯系,相互對立,相互統一,數學分析中的無限只有在與有限的辯證統一中去考慮,才能被理解,才能被應用。

