基于CEEMDAN 排列熵與SVM 的螺旋錐齒輪故障識別?

蔣玲莉， 譚鴻創， 李學軍， 雷家樂

（1.湖南科技大學機械設備健康維護省重點實驗室 湘潭，411201）（2.佛山科學技術學院機電工程與自動化學院 佛山，528225）

引 言

螺旋錐齒輪傳動因其重疊系數大、承載能力強、傳動比高、傳動平穩和噪聲小等優點，被廣泛應用于航空、汽車和礦山等機械傳動領域，是機械工程中重要的基礎傳動件。由于制造和裝配誤差，以及運行過程中的潤滑不良和超速超載工作等因素，螺旋錐齒輪易發生損傷和故障，由此導致振動異常等，影響整個傳動系統的正常運行。對螺旋錐齒輪的運行狀態進行監測和診斷，確保整個傳動系統安全、高效、穩定運行，具有重要的現實意義。

由于螺旋錐齒輪副嚙合對數、嚙合點位置及瞬時傳動比不斷變化，輪齒在嚙合過程中不斷撞擊，因此振動信號異常復雜，故障出現時信號更是呈現強非線性非平穩特性，故障特征信息被淹沒在強噪聲中，非常微弱，難以識別，是其故障診斷的難點［1-2］。為了實現螺旋錐齒輪故障的有效診斷，近年來國內外學者開展了部分螺旋錐齒輪典型故障診斷研究［3-5］，主要集中在基于小波分解的特征提取上，例如基于離散小波弧齒錐齒輪的故障診斷方法［4］以及自適應提升多小波的螺旋錐齒輪的故障診斷方法等［5］。總體來說，相對于平行軸齒輪系及行星輪系齒輪故障診斷研究，交叉軸螺旋錐齒輪故障診斷方法研究還不夠深入［6-7］。

繼小波分解后，經驗模態分解（empirical mode decomposition，簡稱EMD）在工程實際中被證明是優于小波分解的信號處理方法［8］，適用于螺旋錐齒輪故障特征提取，但存在模態混疊問題。Wu 等［9］對EMD 進行了改進，提出集總經驗模態分解（ensemble empirical mode decomposition，簡 稱EEMD）。EEMD 在一定程度上有效緩解EMD 分解模態混疊現象，但由于EEMD 加入高斯白噪聲，無法得到IMF 精確重建原始信號，使分解得到的IMF 數量不盡相同，且存在迭代運行高、計算效率低的問題。互補集總經驗模態分解（complementary ensemble empirical mode decomposition，簡稱CEEMD）［10］解決了EEMD 無法精確重構的問題，可極大降低重構誤差，提高計算效率，但存在產生不同數量IMF 的弊端。針對以上算法的缺陷，自適應噪聲完備經驗模態 分解［11］是對EMD，EEMD 和CEEMD 的發展和繼承，其在執行分解的各階段添加自適應的高斯白噪聲，消除虛假的IMF，重構誤差接近于0，分解效率高且極其完整［12-13］。

通過EMD，EEMD，CEEMD 和CEEMDAN 分解獲得IMF 構造敏感特征量，是故障診斷領域行之有效的方法，例如以IMF 能量、熵和能量熵等為典型故障敏感特征量［14-15］。隨著熵理論的發展，排列熵（permutation entropy，簡稱PE）［16］被提出，其具有計算量少、魯棒性強等特點，可以用于檢測時間序列隨機性、復雜性以及振動信號突變［17-18］，已在機械故障診斷領域初步應用。施瑩等［19］為提高列車輪軸承故障診斷效率，提出排列熵與EEMD 相結合的方法。丁闖等［20］研究行星齒輪箱3 種狀態的排列熵，提出局部均值分解和排列熵的行星齒輪箱故障診斷方法。螺旋錐齒輪在故障狀態下運行時，其振動信號復雜多變，而排列熵可在復雜多變的運動中找到規律，CEEMDAN 排列熵可作為螺旋錐齒輪故障敏感特征量，用于其狀態識別。

由于螺旋錐齒輪早期故障特征信息微弱，關鍵信息完全淹沒在噪聲中，在進行故障特征提取之前，僅檢測待測信號的動力學突變難以準確實現故障辨識，筆者結合SVM 開展螺旋錐齒輪故障狀態識別研究。在深入研究CEEMDAN 和排列熵的基礎上，針對螺旋錐齒輪故障機理及其振動信號特征，將實測信號用CEEMDAN 得到若干IMF，利用相關系數計算各IMF 分量與原始信號的相關程度，結合信噪比的大小，提取包含主要故障信息的IMF 的排列熵，作為特征向量輸入SVM，通過SVM 進行故障狀態分類與識別，實現螺旋錐齒輪典型故障的診斷。

1 基本理論

1.1 CEEMDAN 基本原理

CEEMDAN 通過向原始信號進行EMD 的各階段添加自適應的高斯白噪聲，消除虛假的IMF。令Mk(?)為經過EMD 所產生的第k個內稟模態函數，CEEMDAN 產生的第k個內稟模態函數定義為則CEEMDAN 的分解流程如下。

1）令原始時間序列信號為y(n)，加入高斯白噪聲wi(n) 得 到 新 信 號yi(n) =y(n) +γ0wi(n)，其中，γ0為噪聲標準差。CEEMDAN 對信號yi(n)執行I次分解，得到第1 階內稟模態函數為

2）在分解的第1 階段(k=1)得到第1 階余量信號，即

3）對新的余量信號r1(n) +γ1M1(wi(n) )進行EMD，得到第1 個內稟模態函數時停止，獲得CEEMDAN 的第2 個內稟模態函數為

4）以此類推，當k=2，3，…，K時，第k個余量信號為

對rk(n)進行EMD，得到第1 階內稟模態函數時停止，獲得CEEMDAN 的第k+1 個內稟模態函數為

5）多次執行步驟4，直至余量不能繼續分解，即余量信號的極值點個數最多為兩個。最終的余量滿足

其中：K為CEEMDAN 算法分解所得到的內稟模態函數個數。

因此，原始時間序列信號y(n)可表示為

1.2 排列熵基本原理及參數選取

1.2.1 排列熵原理

熵可用于描述數據信息的不確定性，而排列熵具有可準確刻畫復雜時間序列突變性的特點，對動態的數據變化有很強的敏感性，通過排列熵值的變化來反映設備的不同運行狀態，從而達到異常檢測的目的，其算法過程如下。

假設長度為N的時間序列 {a(i)，i=1，2，…，N}，對其進行相空間重構，得到新的重構矩陣H為

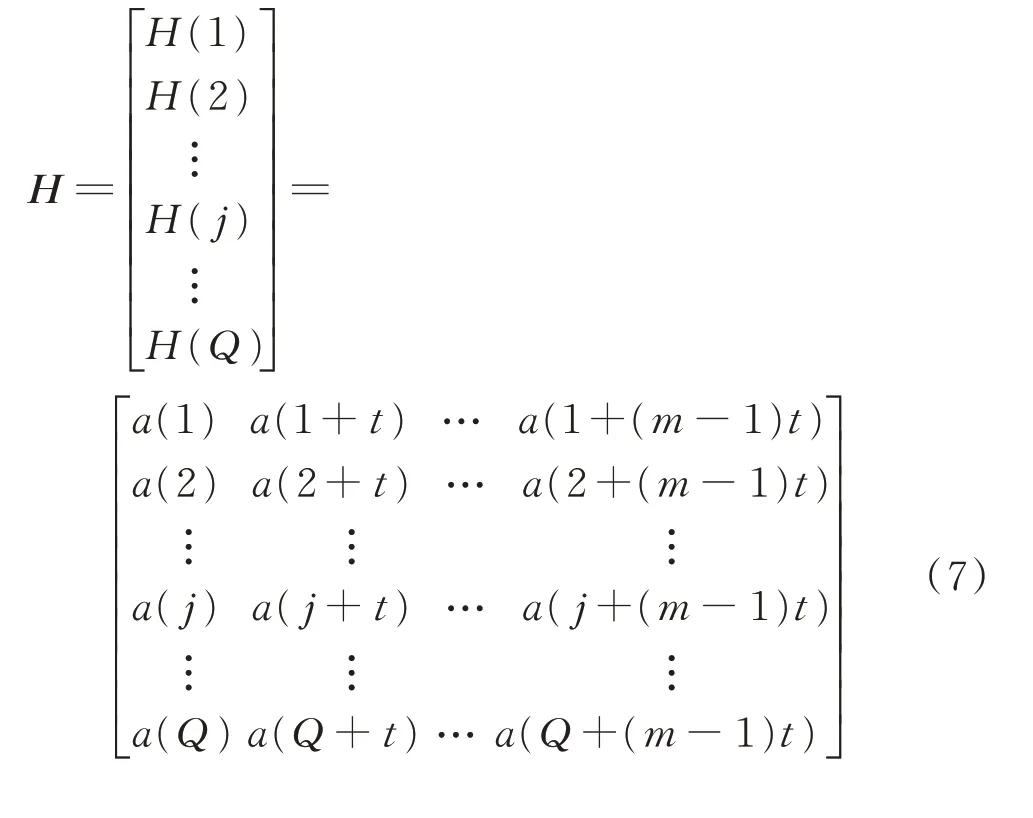
其中：j=1，2，…，Q；m為嵌入維數；t為時延；Q+(m?1)t=n。

將重構矩陣H中的第j個重構分量H(j)={a(j)a(j+t)a(j+(m?1)t)}按照升序重新排列，即

其中：i1，i2，…，im為H（j）分量中元素所在列的位置。

如 果 存 在a(j+(ie?1)t)=a(j+(ic?1)t)，則按照e，c的大小來排序，即e＞c時，有a(j+(ie?1)t)≥a(j+(ic?1)t)；反之亦然。

因此，任意一個包含于重構矩陣H分量H（j）都可得到對應的位置序列

其中：q≤m！；S（j）為m！種代碼序列中的一種。

m個不同的代號[i1，i2，…，im]有m！種不同的排列組合，即有m！種不同的符號序列。

當Pj=1/m時，LPE(m)取得最大值ln(m！)。借助ln(m！)將排列熵LPE(m)進行標準化處理，即

其中：0 ≤LPE≤1。

LPE值的大小表示一維時間序列的隨機性程度。LPE越大，說明時間序列隨機性越強；反之，則說明時間序列規律性越強。

1.2.2 重疊組合法優選排列熵參數

在排列熵運算中，不同參數的設置會對計算結果產生影響，選取最佳的嵌入維數m和時延t是螺旋錐齒輪排列熵特征提取的關鍵。

圖1 不同m，t 的排列熵Fig.1 Permutation entropy of different m and t

通過對不同運行狀態螺旋錐齒輪原始振動信號進行對比，發現當嵌入維數m=4，5，6，時延t=1，2，3 時，排列熵對振動信號的細微突變更敏感。圖1 為不同m，t的排列熵。由于嵌入維數和時延的選擇都會對排列熵計算結果產生影響，僅考慮單一參數的變化缺乏合理性，故筆者采用重疊組合法確定嵌入維數m和時延t，即將螺旋錐齒輪的一段原始振動信號按照時間序列分成一系列的子序列w1，w2，…，wn，w1向后移動一個數據點得到w2，以此類推，用一對嵌入維數m和時延t計算排列熵值。由于較大的w不能精確反映出信號的變化，而較小的w不僅效率低且無統計意義，故選擇w=128。圖1（a）為采樣頻率為16384 Hz 的螺旋錐齒輪正常狀態與故障狀態原始振動信號的組合，0～1 s 為正常齒輪狀態，1～2 s 為2/3 斷齒狀態。由圖1 可知：在正常狀態下螺旋錐齒輪振動信號充滿隨機性，排列熵較大；在斷齒故障時，振動沖擊相對有規律，排列熵值較小；排列熵可以表述振動信號的突變。對比圖1（b），（c），（d）可知：在時延t=1，2，嵌入維數m=4，5 時，排列熵均能有效放大微弱的信息突變，較好地區分出螺旋錐齒輪正常與2/3 斷齒狀態；當t=1，m=4 時最能體現螺旋錐齒輪正常狀態到2/3 斷齒狀態的突變。故筆者選擇排列熵時延t=1，嵌入維數m=4。

2 基于CEEMDAN 排列熵與SVM 的螺旋錐齒輪故障診斷

螺旋錐齒輪傳動系統振動信號異常復雜，故障信號呈強非線性非平穩特性，通過以CEEMDAN 分解所得IMF 的排列熵為特征向量，以SVM 為分類器進行齒輪故障分類與識別。CEEMDAN 分解可得到一系列IMF，而故障信息主要集中在少數的IMF中，以各階IMF 與CEEMDAN 分解前信號的相關系數為依據，結合信噪比進行IMF 優選，選取相關系數大且信噪比高的IMF 分量，并計算其排列熵，作為輸入SVM 的特征向量，在確保診斷精度的同時，提高計算速度。基于CEEMDAN 排列熵與SVM 的螺旋錐齒輪故障診斷流程如圖2 所示，具體步驟如下。

1）原始振動信號采集。采集螺旋錐齒輪典型故障狀態下的振動信號，作為后續分析的原始時間序列信號。

2）CEEMDAN 分解。對不同故障狀態下的原始振動信號進行CEEMDAN，得到一系列IMF。

3）有效IMF 優選。計算各階IMF 與CEEMDAN 信號的相關系數，結合信噪比，選取相關系數大且信噪比高的IMF 分量。

圖2 診斷流程圖Fig.2 Diagnosis flow chart

4）排列熵計算。計算優選IMF 的排列熵，組成多維特征向量[LPE1，LPE2，…，LPEh]。

5）SVM 分類器訓練。以第4 步獲得的特征向量對SVM 進行訓練，獲得典型故障狀態分類器。

6）故障識別。重復步驟1～4，獲得訓練樣本的多維特征向量，利用SVM 分類器進行故障狀態識別，實現故障診斷。

3 試驗驗證

以螺旋錐齒輪典型故障診斷實例來驗證本研究方法的有效性。用于典型故障狀態振動信號采集的螺旋錐齒輪箱試驗臺如圖3 所示。該試驗臺由調速器、電機、聯軸器、一對螺旋錐齒輪和負載5 部分組成，主動齒輪齒數為10，從動齒輪齒數為30。以主動齒輪為試驗齒輪，分別裝置正常齒輪、1/3 斷齒和2/3 斷齒來模擬3 種斷齒故障狀態，如圖4 所示。

使用B&K 公司的PULSE 數據采集系統進行振動信號采集。試驗過程中，通過調節調速器使電機的轉速恒定為1200 r/min，采集3 種不同程度斷齒故障狀態、相同負載下的振動信號，采樣頻率為16384 Hz，取輸入軸支撐軸承處的軸向振動信號進行分析。

圖3 螺旋錐齒輪箱試驗臺Fig.3 Spiral bevel gear box

圖4 3 種斷齒故障狀態Fig.4 Three kinds of broken tooth fault states

3 種狀態時域信號如圖5 所示。可見，相比正常狀態，幅值峰值明顯增大，且隨著斷齒程度的加重，輪齒嚙合時振動沖擊最明顯。

圖5 3 種狀態時域信號Fig.5 Three state time domain signals

對3 種斷齒故障狀態下的螺旋錐齒輪振動信號進行CEEMDAN，其噪聲標準差為0.19，總體平均次數為100。限于篇幅，僅展示1/3 斷齒故障的CEEMDAN 結果，如圖6 所示。由圖6 可知，原始振動信號被分解成13 個IMF，其中第13 個分量為余項，從IMF1到IMF12波形的混疊現象逐漸減弱，頻率也是由高到低分布。

各IMF 序列的排列熵如圖7 所示。由圖7 可知，IMF1～IMF13的排列熵逐漸變小，排列熵越大，說明時間序列隨機性越強；反之，則說明時間序列規律性越強。隨著IMF 階數增大，其頻率成分越來越單一，表現出更強的規律性，與理論分析結果基本吻合。

圖6 1/3 斷齒故障的CEEMDAN 結果Fig.61/3 broken tooth fault of CEEMDAN result

圖7 各IMF 序列排列熵Fig.7 Permutation entropy of each IMF sequence

分別計算1/3 斷齒原始振動信號與其CEEMDAN 所得各階IMF 的相關系數與信噪比，如表1 所示。從表1 可知，前2 階IMF 與原始振動信號的相關程度比較高，都在0.6 以上；信噪比在?8 dB 以上，故優選前兩階IMF。

計算3 種不同程度斷齒故障狀態CEEMDAN前兩階IMF 的排列熵，取時延t=1，嵌入維數m=4，信號長度N=4096。3 種狀態部分樣本的CEEMDAN 排列熵對比結果如圖8 所示。由圖8 可知，優選IMF 的排列熵對螺旋錐齒輪3 種典型斷齒故障狀態有較好的區分度。

將優選IMF 的排列熵值作為特征向量輸入SVM 分類器進行訓練，每種故障狀態取40 個樣本，共120 個樣本作為訓練樣本。SVM 設置3 個兩類向量機分類器，將3 類狀態的排列熵特征向量輸入向量機，把螺旋錐齒輪正常狀態標簽設為“1”，1/3 斷齒狀態設為“2”，2/3 斷齒狀態設為“3”。SVM 核函數采用徑向基函數（radial basis function，簡稱RBF），使用交叉驗證的網格搜索方法尋找最優的懲罰因子和核函數參數，避免了人為設置的經驗性缺陷。

表1 各IMF 的相關系數和信噪比Tab.1 Correlation coefficient and signal to noise ratio of each IMF

圖8 3 種狀態CEEMDAN 排列熵對比Fig.8 Comparison of three states CEEMDAN permutation entropy

每種故障狀態取40 個樣本，共120 個樣本作為測試樣本，輸入訓練好的SVM 分類器進行分類識別，CEEMDAN 排列熵診斷結果如圖9 所示，準確率高達100%。

圖9 CEEMDAN 排列熵診斷結果Fig.9 CEEMDAN permutation entropy diagnosis result

為了驗證基于CEEMDA 排列熵螺旋錐齒輪故障診斷方法的優越性，將上述3 種狀態螺旋錐齒輪振動信號分別使用EEMD 和EMD，計算前兩階IMF 的排列熵。使用相同參數設置的EEMD 并計算前兩階IMF 的排列熵如圖10 所示。由圖10 可知，EEMD 排列熵對螺旋錐齒輪3 種不同程度斷齒故障狀態的區分度明顯劣于圖9 所示的CEEMDAN 排列熵。以EEMD 排列熵構造多維特征向量輸入SVM 分類器進行訓練與測試，診斷結果如圖11 所示，總體分類結果僅為88.33%。其中：在標簽1 中，即螺旋錐齒輪正常狀態，40 個測試樣本中有7 個樣本識別出錯；在標簽2 中，即1/3 斷齒狀態，40個測試樣本中有7 個樣本識別出錯；在標簽3 中，即2/3 斷齒狀態，識別完全正確。

按照上述同樣的方法，3 種狀態螺旋錐齒輪振動信號分別經EMD，提取并計算IMF1與IMF2的排列熵構造特征向量，輸入支持向量機進行訓練與測試。EMD 排列熵診斷結果如圖12 所示，總體分類結果僅為83.33%。其中：在標簽1 的40 個測試樣本中，有5 個樣本識別出錯；在標簽2 的40 個測試樣本中，也有5 個樣本識別出錯；在標簽3 中有10 個樣本識別出錯。

分析可知，以CEEMDAN 的優選IMF 排列熵為特征向量，對螺旋錐齒輪3 種不同程度斷齒故障的診斷準確率明顯高于EEMD 和EMD 的分析結果，說明了CEEMDAN 在螺旋錐齒輪斷齒故障診斷中的優越性。

為了進一步說明CEEMDAN 排列熵的優越性，用EEMD 和EMD 將上述3 種狀態螺旋錐齒輪振動信號進行分解，計算IMF1～IMF3，…，IMF1～IMF8的排列熵，并組成高維特征向量輸入SVM 進行識別，結果如表2 所示。由表2 可知，利用EEMD 需要提取前7 階IMF 排列熵才能正確識別3 種狀態螺旋錐齒輪，而在同樣的特征提取方法下，CEEMDAN僅需提取前兩階IMF 的排列熵。特征向量維數越高，SVM 的訓練與測試所需的時間越長，同樣體現了CEEMDAN 的優越性。

圖10 3 種狀態EEMD 排列熵對比Fig.10 Comparison of three states EEMD permutation entropy

圖11 EEMD 排列熵診斷結果Fig.11 EEMD permutation entropy diagnosis results

圖12 EMD 排列熵診斷結果Fig.12 EMD permutation entropy diagnosis results

表2 EEMD 排列熵和EMD 排列熵的準確率Tab.2 Accuracy of EEMD permutation entropy and EMD permutation entropy

4 結束語

提出一種基于CEEMDAN 排列熵與SVM 的螺旋錐齒輪故障診斷方法，并以實例分析驗證了該方法的有效性。分析結果表明：CEEMDAN 排列熵對螺旋錐齒輪的不同程度斷齒故障狀態具有很好的區分度，可作為敏感特征量用于螺旋錐齒輪故障診斷；以優選的CEEMDAN 排列熵為特征向量，結合SVM可獲得滿意的螺旋錐齒輪不同程度斷齒故障分類診斷結果，且明顯優于EEMD 和EMD 的分析結果。