特殊螺紋接頭各向異性試驗載荷包絡線的計算

陳玉鵬，呂春莉，駱靜輝

（天津鋼管制造有限公司，天津300301）

0 引言

特殊螺紋接頭（premium connection）是在API螺紋接頭基礎上發展起來的，目的在于克服API 螺紋在性能上的缺陷，它適用于各種復雜應力環境，經驗表明特殊螺紋接頭在使用中表現出了優異的性能[1-2]。基于ISO 13679 或API 5C5 的接頭全尺寸評價試驗是評價特殊螺紋接頭性能的基本方法，全尺寸試驗主要包含三個方面的內容：上卸扣試驗、密封試驗和極限載荷試驗。其中密封試驗需要利用Mises 等效應力公式構造試驗載荷包絡線，用于表征接頭的極限性能并計算試驗需要的載荷。

隨著試驗標準的不斷升級，耐蝕合金油井管的各向異性已經引起了重視，在新版API 5C5 2017 標準中已經提出了相關問題[3]。但標準并未給出明確的計算方法，只是提及如果進行橫向拉伸或者壓縮試驗，試驗的最小屈服強度可用于計算接頭評價試驗載荷包絡線。近幾十年來，各向異性屈服準則的理論研究得到很大發展，常用的各向異性屈服準則分為三個系列，即Hill 系列、Hosford 系列和Drucker系列，其中Hill48 屈服準則應用最為廣泛[4]。

本文以一種超級雙相不銹鋼管為研究對象，通過力學性能試驗，研究了這種高合金材料的各向異性。根據試驗數據，利用Hill48 各向異性屈服準則計算了試驗載荷包絡線。對于具有各向異性的高合金油井管，該計算方法可用于確定特殊螺紋接頭全尺寸評價試驗的試驗載荷。

1 試驗內容及方法

1.1 力學性能試驗

本文研究了一種125KSI 鋼級SAF2507 超級雙相不銹鋼管，其規格為φ250.83 mm×16.97 mm，通過冷拔工藝加工至成品管尺寸。在管體周向四個象限內分別取四象限軸向拉伸試樣和壓縮試樣，橫向拉伸及壓縮試樣，試樣尺寸均為φ6.25 mm 圓棒試樣。試樣尺寸如圖1 所示。在材料萬能試驗機上進行拉伸及壓縮試驗。試驗過程參照ASTM A370 試驗標準要求。其中壓縮試驗在達到規定總應變量以后，停止加載。將非比例延伸強度Rp0.2作為材料的屈服強度。通過比較此種材料在不同方向上的屈服強度差異來研究材料的各向異性問題。

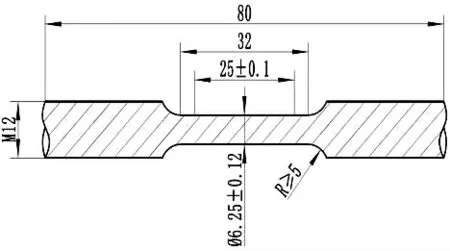
圖1 試樣尺寸，單位：mm

2.2 HILL 各向異性屈服準則的應用

屈服準則是判定材料中某點的應力分量滿足一定關系后產生塑性變形的依據。1948 年，Hill 在Mises 屈服準則基礎上，將各向異性引入屈服函數中，提出了Hill1948 各向異性屈服準則，簡稱Hill48屈服準則[5]。其表達式如下：

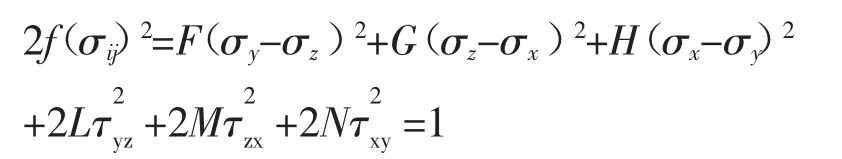
其中f（σij）為應力張量函數，F、G、H、L、M、N為描述各向異性的常數。σx、σy、σz、τyz、τzx、τxy為9 個應力分量。當F=G=H=1，L=M=N=3 時，HILL48 屈服準則與Mises 屈服準則的表達式完全相同。

對于管材而言，因所研究載荷只涉及軸向載荷及壓力，故只考慮正交方向三個主應力，各向異性的主方向分別位于軸向x、環向y及徑向z，綜上可得出屈服準則的表達式為：

式中：σa為軸向應力；σh為環向應力；σr為徑向應力。

如果X，Y，Z分別表示各向異性主方向上的屈服強度，則HILL 各向異性常數與各個方向上的屈服強度的關系為：

在基于Mises 屈服準則的試驗載荷包絡線中，試驗載荷被分成四種組合形式，分別位于十字坐標軸的四個象限內：第一象限包含拉伸+內壓，第二象限包含壓縮+內壓，第三象限包含壓縮+外壓，第四象限包含拉伸+外壓。Hill 各向屈服準則考慮了三個方向上的各向異性，但并不區分拉伸和壓縮。如果將四個象限分別應用Hill 公式，可計算出相似形式的試驗載荷包絡線。如前文所述，由于徑向應力并不能通過試驗直接得到，這里可進行簡化處理，第一，在徑向上不會產生拉應力，即在內壓和外壓作用下，在徑向上永遠是壓應力。第二，根據相關經驗及數據顯示，徑向壓縮屈服強度可視作與軸向拉伸屈服強度相等。則只要分別計算出每個象限的各向異性常數F、G、H，最后將Lamè 公式及軸向應力帶入Hill 屈服準則表達式（不考慮彎曲應力），即可計算出每個象限的壓力與軸向載荷的關系函數表達式。

軸向應力公式：σa=Fa/AP

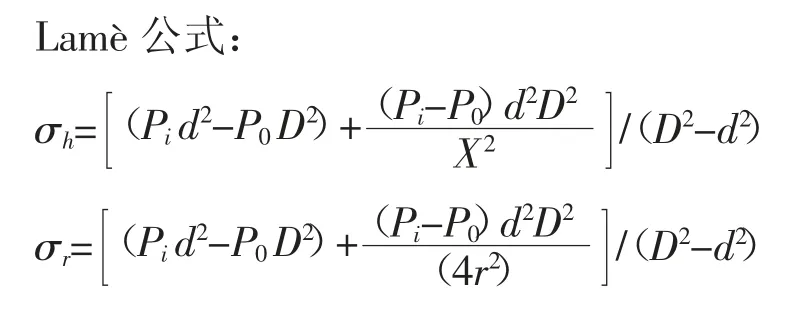
其中：Fa：軸向載荷；Ap：管體橫截面積；D：管子外徑；d：管子內徑，d=D-2t；t：管子壁厚；Pi：內壓；P0：外壓；r：徑向坐標，（d/2）≤r≤（D/2）。

2 試驗結果及討論

2.1 拉伸及壓縮試驗

縱向和橫向拉伸壓縮力學性能試驗結果表明，冷加工的SAF2507 超級雙相不銹鋼具有明顯的各向異性。表1 為拉伸及壓縮試驗數據表。圖2 比較了材料在不同試驗中的平均屈服強度。其中橫向壓縮屈服強度最高，達到1 006 MPa，縱向壓縮屈服強度最低僅有852 MPa，相差154 Mpa；縱向拉伸和壓縮屈服強度也存在較大差異，兩者相差137 MPa。在進行試驗載荷計算時，如果仍按照傳統的試驗載荷計算方法，即將材料壓縮屈服強度等同于拉伸屈服強度，那么會造成接頭在軸向壓縮載荷下發生失穩的可能性變大。

表1 拉伸/壓縮試驗數據

圖2 SAF2507 超級雙向鋼平均屈服強度對比

2.2 各向異性試驗載荷包絡線的計算

根據力學性能試驗結果，選擇每個方向上的最小屈服強度，使用管體名義外徑及壁厚，計算了各向異性材料管體試驗載荷包絡線（特殊扣接頭全尺寸評價試驗載荷包絡線通常根據管體確定，即假設接頭的性能與管體等同）。圖3 為各向異性接頭名義試驗載荷包絡線與各向同性接頭名義試驗載荷包絡線對比圖。名義試驗載荷包絡線即為100%效率。表2 為兩種計算公式根據ISO13679 A 系試驗載荷點計算的具體數值，其中軸向載荷及內壓基于95%載荷包絡線，外壓基于API 擠毀壓力。

圖3 各向異性接頭試驗載荷包絡線對比圖

2.3 各向異性試驗載荷包絡線的分析

從圖3 的對比圖中可以看出，利用Hill48 各向異性屈服準則計算的接頭試驗載荷包絡線充分體現了材料在縱向和橫向、拉伸及壓縮中表現出的性能，客觀的表現出材料的各向異性差異。如第一象限中，材料受到軸向拉伸載荷及內壓載荷，內壓在管子上產生環向拉應力及徑向應力，由于材料實測橫向拉伸屈服強度小于縱向拉伸屈服，而橫向拉伸屈服強度對應環向拉應力，則反映在曲線上為Hill公式計算的內壓載荷小于基于各向同性的Mises 公式計算的內壓值。又如第三象限，材料受壓縮載荷及外壓載荷，外壓在管子上產生環向壓應力及徑向應力，根據實際的力學性能測試結果，壓縮屈服強度小于拉伸屈服強度，則反映在圖中為Hill 公式計算的材料的極限壓縮載荷與實測值相等，并且小于各向同性的壓縮載荷。橫向壓縮屈服強度對應外壓產生的環向壓應力，而實測的試驗結果為橫向壓縮屈服強度最高，計算出的外壓值也更大。第二、四象限的計算結果類似。

需要注意的是在縱坐標上，第一、二象限交界處，當軸向載荷為零時，內壓處曲線出現了不連續的情況，計算內壓值分別為117.6 MPa 及120 MPa。原因在于針對徑向屈服強度的簡化處理，即將徑向屈服強度等同于縱向拉伸屈服強度。而在應用Lamè公式時，最大應力通常產生于管子的內表面，即r=d/2 時，此時內壓在內表面產生的徑向應力為-Pi，而外壓在內表面產生的徑向應力為0，也就是說徑向屈服強度對于外壓來講沒有任何影響，所以外壓作用時，曲線在第三和第四象限的坐標軸上是相交的，并沒有產生不連續的現象。另一方面，在API 5C3 油套管性能計算標準附錄A 中已指出，將屈服準則簡化為兩種特殊情形即分別考慮內壓和外壓，造成了圖形在Pi=P0=0 時，在坐標軸交點處過渡并不是光滑的，原因在于計算環向應力及徑向應力時Lamè 公式本身內在的影響。如果不存在材料性能的各向異性，那么Hill 公式計算出的試驗載荷包絡線與Mises 等效應力公式計算出的包絡線是完全重合的。

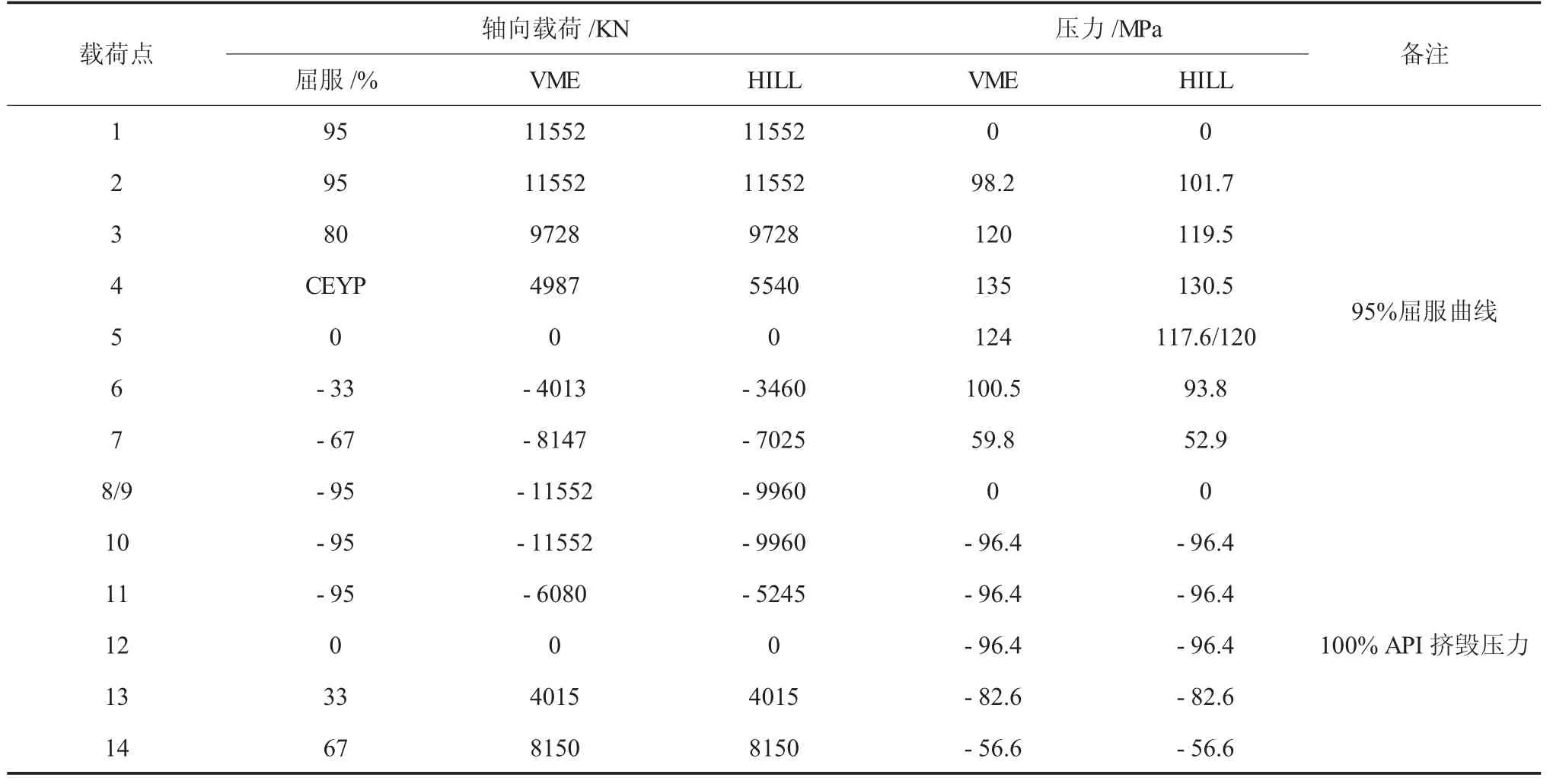
表2 ISO13679 A 系試驗載荷點

綜上所述，利用Hill48 屈服準則計算出的各向異性材料接頭評價試驗載荷包絡線，客觀的反映出了材料實測力學性能的表現，具有較強的合理性。

3 結論

本文通過力學性能試驗，對SAF2507 超級雙相不銹鋼的各向異性進行了研究，并根據試驗數據，計算了基于Hill 各向異性屈服準則的特殊扣接頭評價試驗包絡線。結果顯示，利用Hill 公式計算的試驗載荷包絡線是相對合理的，該曲線能夠客觀體現實驗材料的各向異性差異。因此，該計算方法可應用到高合金油井管特殊扣接頭全尺寸評價試驗中去，同時對保證試驗的安全性具有重要的意義。