任意階高運(yùn)算恒定性分抗逼近電路
——標(biāo)度格型級(jí)聯(lián)雙口網(wǎng)絡(luò)

張?jiān)聵s 袁曉

(四川大學(xué)電子信息學(xué)院, 成都 610065)

標(biāo)度拓展經(jīng)典負(fù)半階分抗逼近電路, 可實(shí)現(xiàn)具有任意分?jǐn)?shù)階微積算子運(yùn)算功能的分抗逼近電路, 但犧牲了運(yùn)算恒定性.從電路網(wǎng)絡(luò)的角度分析具有恒定運(yùn)算性能的負(fù)半階Carlson 分形格分抗逼近電路.根據(jù)標(biāo)度分形格分抗逼近電路的等效無(wú)源雙口網(wǎng)絡(luò), 探討該雙口網(wǎng)絡(luò)右側(cè)端口的運(yùn)算有效性, 設(shè)計(jì)具有高運(yùn)算恒定性的任意階標(biāo)度分形格分抗逼近電路.結(jié)合負(fù)實(shí)零極點(diǎn)對(duì)基元系統(tǒng)的零極點(diǎn)分布及其局域化特性, 闡述具有任意實(shí)數(shù)階微積算子運(yùn)算功能的標(biāo)度分形格分抗逼近電路運(yùn)算振蕩現(xiàn)象的物理本質(zhì), 并從理論上分析有效抑制頻域運(yùn)算振蕩現(xiàn)象的方法.結(jié)合對(duì)稱阻容T 型節(jié)電路優(yōu)化理論及方法, 對(duì)任意階對(duì)稱格型級(jí)聯(lián)雙口網(wǎng)絡(luò)的頻域逼近性能進(jìn)行優(yōu)化, 獲得具有高逼近效益的任意階標(biāo)度分形格分抗逼近電路.具有低振蕩幅度的任意階對(duì)稱格型級(jí)聯(lián)雙口網(wǎng)絡(luò)為高運(yùn)算恒定性的分抗逼近電路設(shè)計(jì)及應(yīng)用提供了一種新方法及思路.

1 引 言

分?jǐn)?shù)階微積分適用于描述自然界中大多數(shù)非線性, 非整數(shù)維物理現(xiàn)象及過程.由于階次取值更加靈活, 分?jǐn)?shù)階系統(tǒng)更能準(zhǔn)確刻畫非線性問題及其物理本質(zhì), 例如電化學(xué)分析[1,2]、擴(kuò)散過程[3–5]、信號(hào)處理[6–8]等.分?jǐn)?shù)階微積分廣泛應(yīng)用于非線性控制系統(tǒng)[9,10]、分?jǐn)?shù)階混沌系統(tǒng)[11,12]及神經(jīng)網(wǎng)絡(luò)[13]等各種非整數(shù)維物理過程的研究.分?jǐn)?shù)階微積分用于擴(kuò)散、概率、粘彈性動(dòng)力學(xué)、遺傳結(jié)構(gòu)等非整數(shù)維物理現(xiàn)象的建模分析等.分?jǐn)?shù)階電路元件或分抗逼近電路是實(shí)現(xiàn)分?jǐn)?shù)階電路與系統(tǒng)的關(guān)鍵組成部分,現(xiàn)有的非整數(shù)階分抗逼近電路幾乎都具有不恒定的運(yùn)算性能, 這勢(shì)必會(huì)影響分?jǐn)?shù)階電路等物理系統(tǒng)的理論與應(yīng)用研究的真實(shí)性[14].

最簡(jiǎn)單的具有兩根引出端線的分?jǐn)?shù)階元器件稱為分抗元, 早期也曾稱恒相元[15].理想 μ 階分抗元的阻抗函數(shù)為

其中s 表示復(fù)頻率變量也稱運(yùn)算變量, F(μ)為理想分抗元的集總特征參量, 簡(jiǎn)稱分抗量.理想分抗元的具體實(shí)現(xiàn)還存在困難, 目前常用的方法是設(shè)計(jì)一個(gè)物理可實(shí)現(xiàn)的有理阻抗函數(shù)序列 { Zk(s)} 逼近理想分抗元的阻抗函數(shù) I(μ)(s).即

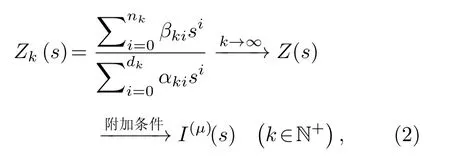
其中k 表示分抗逼近電路的規(guī)模或迭代逼近次數(shù),nk和 dk分別為阻抗函數(shù) Zk(s) 的分子分母多項(xiàng)式的次數(shù), βki和 αki分別表示分子分母多項(xiàng)式系數(shù).現(xiàn)有的經(jīng)典分抗逼近電路如負(fù)半階Oldham 分形鏈分抗逼近電路[16,17], 任意階梯形分抗逼近電路[18],Liu-Kaplan 分形鏈分抗逼近電路[19]等, 都能在一定頻段近似實(shí)現(xiàn)理想分抗的運(yùn)算性能[20].這些電路都來自于自然界、科學(xué)與實(shí)驗(yàn)研究、工程實(shí)踐中的各種物理現(xiàn)象與過程的分析和電路建模.

為便于數(shù)學(xué)上分析分抗逼近電路、分?jǐn)?shù)階系統(tǒng)的運(yùn)算性能和逼近性能, 將阻抗函數(shù) Zk(s) 進(jìn)行歸一化處理.對(duì)于 R C 分抗逼近電路取歸一化復(fù)頻率變量 w =τs , 其中 τ =RC 表示時(shí)間常數(shù).對(duì)(2)式中的 Zk(s) 進(jìn)行歸一化, 得到歸一化阻抗函數(shù)

為便于頻域特征分析,取歸一化復(fù)頻率變量w=j10?,其中j=, ?∈R 表示歸一化頻率指數(shù)變量, 簡(jiǎn)稱頻率變量.將 w =j10?代入歸一化阻抗函數(shù) yk(w) , 得到幅頻、相頻、階頻、F 頻特征函數(shù)分別為:

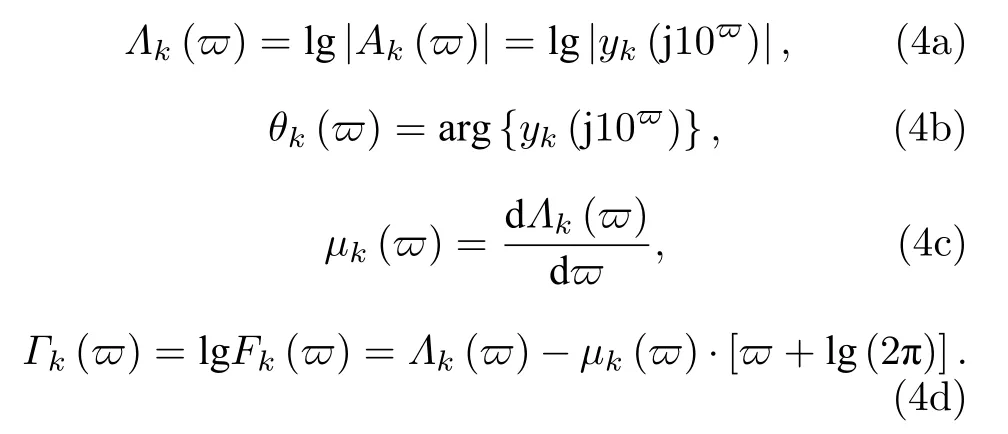
1960 年, Carlson 在研究航空器的線性自適應(yīng)伺服控制系統(tǒng)時(shí), 為使得控制系統(tǒng)的傳輸函數(shù)具有半階積分算子運(yùn)算功能, 提出了負(fù)半階Carlson 分形格分抗逼近電路, 算子 s?1/n的正則迭代逼近法.袁曉[14]將Carlson 正則迭代法推廣為任意階分?jǐn)?shù)算子的有理逼近, 何秋燕等[21–23]對(duì)其運(yùn)算性能與逼近性能做了詳細(xì)分析.結(jié)合標(biāo)度拓展[24]理論, 負(fù)半階Carlson 分形格分抗標(biāo)度拓展后可獲得具有任意實(shí)數(shù)階微積算子運(yùn)算功能的標(biāo)度分形格分抗逼近電路[25,26], 袁曉[14]、He 等[23]和Pu 等[27]提出任意階格型標(biāo)度分憶抗元等新概念及模擬電路實(shí)現(xiàn).這些成果表明, Carlson 格型結(jié)構(gòu)的分抗逼近電路具有許多優(yōu)良的物理性質(zhì).分析任意階標(biāo)度分形分抗逼近電路的頻域特征, 發(fā)現(xiàn)標(biāo)度拓展后的電路在頻域存在固有運(yùn)算振蕩現(xiàn)象[27].這些典型的任意階分抗的階頻特征曲線、相頻特征曲線都有明顯的振蕩波形.運(yùn)算特征曲線的波動(dòng)反映分抗逼近電路的分?jǐn)?shù)階運(yùn)算性能的不恒定性, 振蕩現(xiàn)象勢(shì)必會(huì)影響分抗電路的分?jǐn)?shù)算子逼近性能, 在物理應(yīng)用上造成誤差, 因此必須尋找有效方法克服或抑制分抗逼近電路的運(yùn)算振蕩現(xiàn)象.

本文針對(duì)標(biāo)度拓展后的任意階格型分抗逼近電路的頻域運(yùn)算振蕩現(xiàn)象, 發(fā)現(xiàn)雙口網(wǎng)絡(luò)兩側(cè)端口的級(jí)聯(lián)可以有效抑制運(yùn)算振蕩幅度.首先分析格型級(jí)聯(lián)雙口網(wǎng)絡(luò)兩側(cè)端口的運(yùn)算有效性, 提出抑制運(yùn)算振蕩幅度的電路設(shè)計(jì)新方案.然后分析運(yùn)算振蕩現(xiàn)象產(chǎn)生的本質(zhì)原因, 并在理論上提出減小振蕩幅度的解決思路.結(jié)合分抗逼近電路的電路優(yōu)化理論及方法, 設(shè)計(jì)具有低振蕩幅度、高運(yùn)算恒定性、高逼近效益的任意階格型標(biāo)度分抗逼近電路.最后進(jìn)行總結(jié), 并提出值得進(jìn)一步研究的有關(guān)課題.

2 無(wú)源雙口網(wǎng)絡(luò)——標(biāo)度分形格分抗逼近電路

經(jīng)典Carlson 分形格分抗逼近電路具有負(fù)半階運(yùn)算性能, 歸一化后的Carlson 分形格分抗逼近電路(圖1)是由k 個(gè)基本對(duì)稱格型節(jié)級(jí)聯(lián)而成的雙口網(wǎng)絡(luò).

圖1 中虛線方框中表示單個(gè)基本對(duì)稱格型節(jié).根據(jù)網(wǎng)絡(luò)的傳輸參量矩陣特點(diǎn), 級(jí)聯(lián)后的分抗逼近電路仍然是對(duì)稱的雙口網(wǎng)絡(luò).該分抗逼近電路的運(yùn)算特征曲線如圖2.取 k =32 , 當(dāng)頻率指數(shù)?2.5

圖1 有限k 節(jié)Carlson 格型分抗逼近電路 (a) 歸一化原型電路; (b) 等效雙口網(wǎng)絡(luò)Fig.1.Finite k-stage Carlson Lattice fractance approximation circuit: (a) Normalized prototype circuit; (b) equivalent two-port network.

文獻(xiàn)[25]根據(jù)標(biāo)度拓展理論, 獲得可構(gòu)建具有任意實(shí)分?jǐn)?shù)階微積算子運(yùn)算性能的標(biāo)度化的Carlson 分形格分抗逼近電路—標(biāo)度分形格分抗逼近電路(圖3).圖3 中, α 與 β 分別是電阻遞進(jìn)比與電容遞進(jìn)比, 統(tǒng)稱為標(biāo)度特征參量, σ =αβ 是該電路的標(biāo)度因子.當(dāng) 1 <α,β <∞ 時(shí)為正比標(biāo)度拓展, 當(dāng) 0 <α,β <1 時(shí)為反比標(biāo)度拓展.標(biāo)度分形格分抗逼近電路歸一化電路原理圖及等效的標(biāo)度雙口電路網(wǎng)絡(luò)如圖3.圖3(b)中分抗元 F1,F2表示分抗逼近電路的迭代次數(shù) k →∞ 時(shí)的近似等效理想分抗元, 因此使用區(qū)別于相關(guān)文獻(xiàn)中的理想分抗元的電路符號(hào).

圖3 中歸一化阻抗 yLk(w) , yRk(w) 分別表示網(wǎng)絡(luò)的左右側(cè)輸入阻抗函數(shù).由標(biāo)度分形格分抗逼近電路的結(jié)構(gòu)形式, 其左側(cè)分抗的歸一化阻抗函數(shù)yLk(w)的代數(shù)迭代方程為

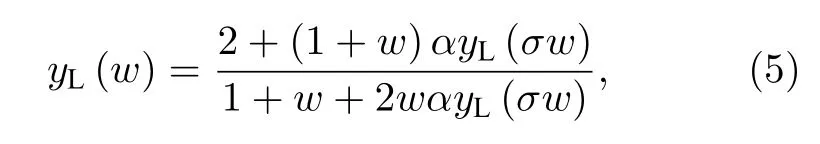
該方程為非正則標(biāo)度方程, 解析求解該方程存在困難.以正比拓展為例, 此時(shí) 1 <α,β,σ <∞.在甚低頻條件 0 ←|w|?1 下, 方程(5)可簡(jiǎn)化為正則標(biāo)度方程

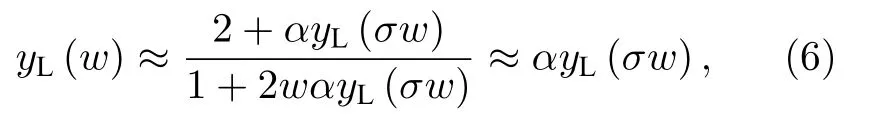
并有近似解析解

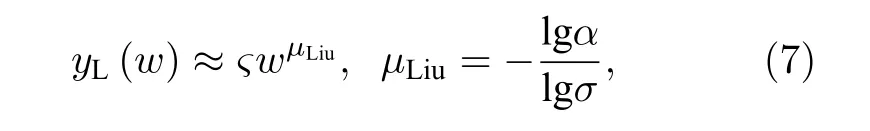
近似解結(jié)果表明左側(cè)端口的等效分抗 F1具有任意Liu 氏運(yùn)算階, 反比拓展時(shí)甚高頻條件下具有相同的近似解結(jié)果.根據(jù)迭代方程(5)可數(shù)值求解該分抗逼近電路的阻抗函數(shù) yL(w) 及其運(yùn)算特征曲線.標(biāo)度拓展后的單節(jié)格型電路是對(duì)稱的雙口網(wǎng)絡(luò), 但每一節(jié)都是不同參量的無(wú)源雙口網(wǎng)絡(luò), 第i 節(jié)對(duì)稱格型基本節(jié)的傳輸參量矩陣

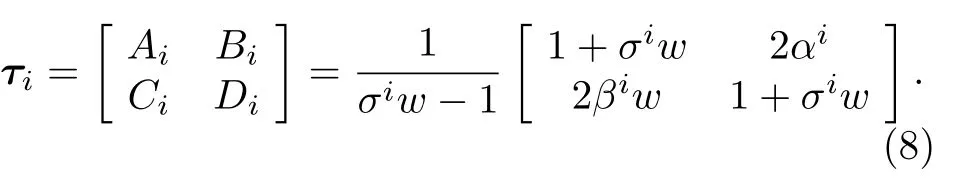
以左側(cè)端口為例, k 節(jié)標(biāo)度格形分抗逼近電路雙口網(wǎng)絡(luò)的傳輸參量矩陣為

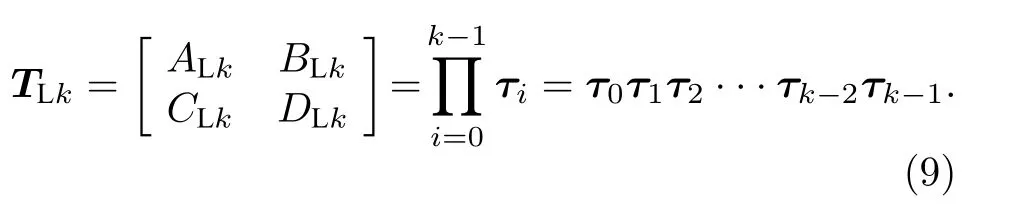
由級(jí)聯(lián)雙口網(wǎng)絡(luò)的傳輸參量矩陣的運(yùn)算關(guān)系, k 節(jié)標(biāo)度格形分抗逼近電路雙口網(wǎng)絡(luò)的右側(cè)端口傳輸參量矩陣為

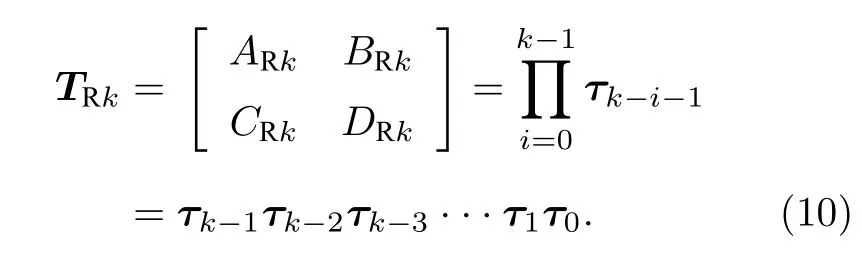
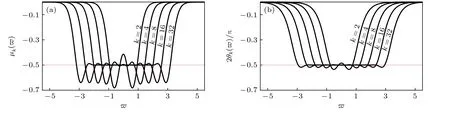
圖2 Carlson 分形格分抗逼近電路的運(yùn)算特征曲線 (a) 階頻特征曲線; (b) 相頻特征曲線Fig.2.Operational characteristic curves of Carlson fractal-lattice fractance approximation circuit: (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.

圖3 k 節(jié)標(biāo)度分形格分抗逼近電路 (a) 歸一化原型電路; (b) 等效雙口網(wǎng)絡(luò)Fig.3.k-stage scaling fractal-lattice fractance approximation circuit: (a) Normalized prototype circuit; (b) equivalent two-port network.

圖4 正比拓展時(shí)左側(cè)端口分抗與右側(cè)端口分抗的運(yùn)算特征曲線( k =12,σ =5 ) (a) 階頻特征曲線; (b) 相頻特征曲線Fig.4.Operational characteristic curves of left-side port fractance and right-side port fractance in direct proportion extension (k =12, σ = 5): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.

圖4 中的運(yùn)算特征曲線表明, 圖3 中的等效雙口網(wǎng)絡(luò)兩側(cè)端口都能夠逼近任意階分?jǐn)?shù)算子, 且具有相同的運(yùn)算階 μLiu和有效運(yùn)算頻段.當(dāng)運(yùn)算階μLiu=?0.5時(shí), 兩側(cè)端口分抗的運(yùn)算特征曲線重合.當(dāng)運(yùn)算階時(shí), 兩側(cè)端口具有不同的運(yùn)算特征曲線.選擇不同端口作為輸入端口, 可以得到不同的任意階分抗逼近電路.標(biāo)度拓展后, 標(biāo)度分形格分抗 F1的運(yùn)算特征曲線在有效運(yùn)算頻段內(nèi)產(chǎn)生了振蕩.該雙口網(wǎng)絡(luò)的右側(cè)分抗 F2同樣具有運(yùn)算振蕩現(xiàn)象, 兩側(cè)分抗具有相同的運(yùn)算振蕩強(qiáng)度與周期 W =|lgσ|.該振蕩現(xiàn)象勢(shì)必影響由分抗元件F 構(gòu)成的分?jǐn)?shù)階電路與系統(tǒng)的運(yùn)算恒定性.因此, 要提高分?jǐn)?shù)階電路與系統(tǒng)的運(yùn)算性能, 應(yīng)當(dāng)消除或抑制分抗元F 的運(yùn)算振蕩現(xiàn)象, 從而提高理論分析與實(shí)踐測(cè)試的真實(shí)性與準(zhǔn)確性.

3 高運(yùn)算恒定性對(duì)稱格型級(jí)聯(lián)雙口網(wǎng)絡(luò)

3.1 對(duì)稱格型級(jí)聯(lián)雙口網(wǎng)絡(luò)

對(duì)稱的負(fù)半階Carlson 分形格原型分抗逼近電路(圖1)的運(yùn)算特征曲線在有效運(yùn)算頻段內(nèi)無(wú)振蕩現(xiàn)象, 運(yùn)算特征曲線呈現(xiàn)恒定的負(fù)半階運(yùn)算性能.電路的等效雙口網(wǎng)絡(luò)具有對(duì)稱性, 左右側(cè)端口完全等價(jià).標(biāo)度拓展后的等效雙口網(wǎng)絡(luò)(圖3)為非對(duì)稱的, 兩側(cè)端口雖然能夠有效逼近分?jǐn)?shù)算子, 但在有效頻段內(nèi)運(yùn)算特征不恒定.由此自然想到, 如果能夠構(gòu)成標(biāo)度拓展后的對(duì)稱無(wú)源雙口網(wǎng)絡(luò), 是否可以有效抑制頻域的運(yùn)算振蕩現(xiàn)象, 獲得具有恒定運(yùn)算性能的任意階分抗逼近電路.

考慮理想情況下, 電路規(guī)模 k →∞.根據(jù)圖3(b)中的等效雙口網(wǎng)絡(luò), 將兩個(gè)相同的標(biāo)度分形格分抗逼近電路的左側(cè)與右側(cè)端口級(jí)聯(lián), 級(jí)聯(lián)后新的等效格型雙口網(wǎng)絡(luò)如圖5.

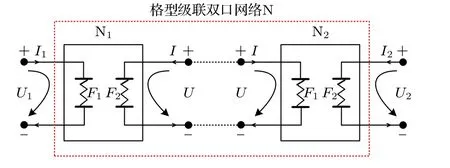
圖5 等效格型級(jí)聯(lián)雙口網(wǎng)絡(luò)NFig.5.Equivalent lattice cascaded two-port network N.

根據(jù)網(wǎng)絡(luò) N1的傳輸參量矩陣

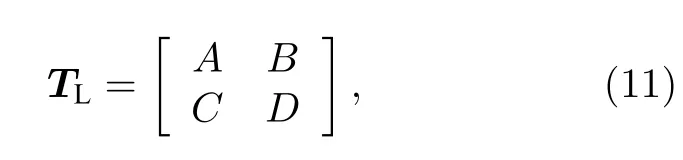
求出網(wǎng)絡(luò) N2的傳輸參量矩陣為

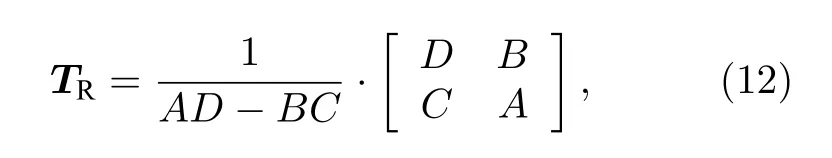
圖5 中級(jí)聯(lián)形成的新網(wǎng)絡(luò)N 的傳輸參量矩陣為

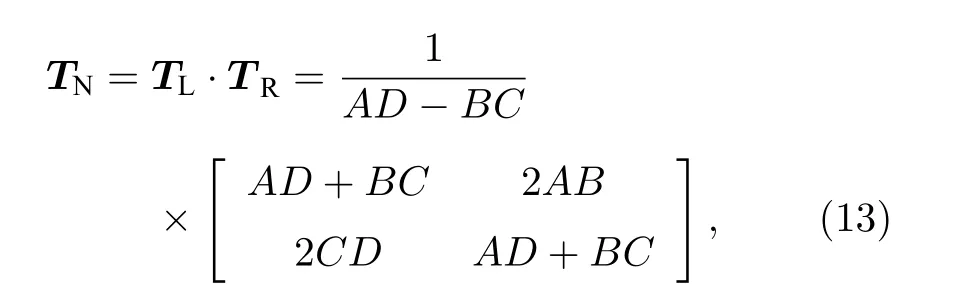
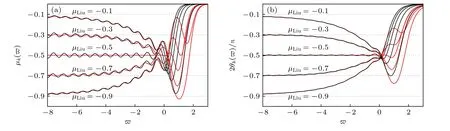
圖6 標(biāo)度分形格分抗與新網(wǎng)絡(luò)N 的運(yùn)算特征曲線( k →∞,σ =5 ) (a) 階頻特征曲線; (b) 相頻特征曲線Fig.6.Operational characteristic curves of scaling fractal-lattice fractance and new network N ( k →∞,σ =5 ): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.

圖7 新網(wǎng)絡(luò)N 的歸一化電路原理圖Fig.7.Normalized circuit schematic diagram of new network N.

并有

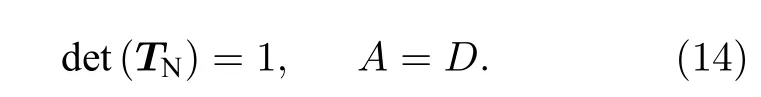
級(jí)聯(lián)后的新網(wǎng)絡(luò)N 是對(duì)稱的, 新雙口網(wǎng)絡(luò)N 的左右兩側(cè)完全等效.負(fù)半階Carlson 分形格原型分抗的等效雙口網(wǎng)絡(luò)是對(duì)稱的, 且具有恒定的運(yùn)算性能.級(jí)聯(lián)后的新網(wǎng)絡(luò)N 的運(yùn)算特征曲線如圖6 中紅色曲線, 相比于標(biāo)度分形格分抗(黑色曲線), 級(jí)聯(lián)后的新網(wǎng)絡(luò)N 的運(yùn)算振蕩幅度明顯減小.

3.2 數(shù)值仿真與實(shí)驗(yàn)結(jié)果分析

設(shè)計(jì)數(shù)值仿真實(shí)驗(yàn), 對(duì)比分析新網(wǎng)絡(luò)N 的運(yùn)算性能與標(biāo)度分形格分抗的運(yùn)算性能.取k 節(jié)標(biāo)度分形格分抗逼近電路, 級(jí)聯(lián)后的歸一化電路原理圖如圖7.當(dāng)初始阻抗 y0(w)=∞ , 電路節(jié)數(shù) k =8 時(shí),正比拓展條件下, 由傳輸參量矩陣數(shù)值求解的新網(wǎng)絡(luò)N 與標(biāo)度分形格分抗的運(yùn)算特征曲線對(duì)比如圖8.紅色曲線表示新網(wǎng)絡(luò)N 的運(yùn)算特征曲線, 黑色為標(biāo)度分形格分抗的運(yùn)算特征曲線.

相比于標(biāo)度分形格分抗逼近電路的頻域曲線,新網(wǎng)絡(luò)N 的頻域運(yùn)算振蕩現(xiàn)象明顯減弱, 振蕩幅度減小, 有效運(yùn)算頻段更寬.實(shí)驗(yàn)仿真表明, 通過標(biāo)度分形格分抗逼近電路的左側(cè)與右側(cè)級(jí)聯(lián), 雖然電路節(jié)數(shù)增加了一倍, 但可以有效抑制分抗逼近電路的運(yùn)算振蕩現(xiàn)象, 獲得恒定的頻域運(yùn)算性能.

4 運(yùn)算振蕩現(xiàn)象及分抗逼近電路的優(yōu)化

4.1 運(yùn)算振蕩現(xiàn)象的理論分析

考慮零點(diǎn)頻率指數(shù)與極點(diǎn)頻率指數(shù)分別為 ?Zi,?Pi的零極點(diǎn)對(duì)組成的一次子系統(tǒng) Ei(?) , 其歸一化阻抗函數(shù)為

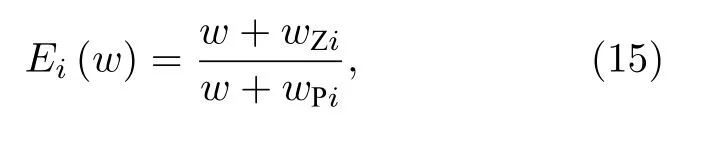
定義零極點(diǎn)比

零極點(diǎn)的中心頻率指數(shù)(幾何中心頻率指數(shù))

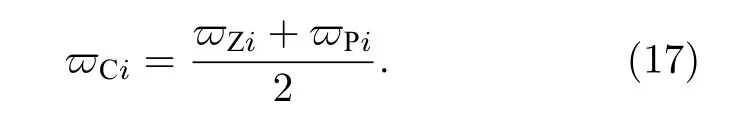
一次子系統(tǒng)的階頻特征函數(shù)和相頻特征函數(shù)[14]:

圖8 新網(wǎng)絡(luò)N 與標(biāo)度分形格分抗運(yùn)算特征曲線對(duì)比圖( k =8,σ =5 ) (a) 階頻特征曲線; (b) 相頻特征曲線Fig.8.Comparison diagram of operational characteristic curves of new network N and scaling fractal-lattice fractance (k = 8, σ =5): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.

圖9 一次子系統(tǒng)的運(yùn)算特征曲線Fig.9.Operational characteristic curves of primary sub-system.

由不同零極點(diǎn)指數(shù)構(gòu)成的負(fù)實(shí)零極點(diǎn)對(duì)基元系統(tǒng)的運(yùn)算特征曲線如圖9.

圖9 中的運(yùn)算特征曲線表明, 每個(gè)一次子系統(tǒng)都具有產(chǎn)生波峰的局域化特性, 頻域的運(yùn)算振蕩現(xiàn)象正是由零點(diǎn)與極點(diǎn)的共同作用導(dǎo)致的.由運(yùn)算特征函數(shù)表達(dá)式(18)式可知, l gαi取值越大, 一次子系統(tǒng)的運(yùn)算振蕩幅度越大.標(biāo)度分形格分抗同樣可以看成由多個(gè)負(fù)實(shí)零極點(diǎn)對(duì)基元系統(tǒng) Ei(?) 組成,頻域的運(yùn)算振蕩現(xiàn)象正是這些一次子系統(tǒng)的集體行為.

從零極點(diǎn)分布的角度分析, 如果能夠減小任意階標(biāo)度分形格分抗的相鄰零極點(diǎn)指數(shù)間隔 l gαi, 理論上便可有效抑制運(yùn)算振蕩幅度, 實(shí)現(xiàn)恒定的運(yùn)算性能.正比拓展 σ =5 , 迭代逼近次數(shù) k =4 時(shí), 不同運(yùn)算階下, 標(biāo)度分形格分抗逼近電路等效雙口網(wǎng)絡(luò)的左側(cè)端口分抗 F1與右側(cè)端口分抗 F2的零極點(diǎn)頻率指數(shù)分布如圖10(a).左側(cè)端口分抗 F1與新網(wǎng)絡(luò)N 的單側(cè)端口分抗的零極點(diǎn)指數(shù)分布對(duì)比如圖10(b).

由圖10(a)可以看出, 標(biāo)度分形格分抗等效雙口網(wǎng)絡(luò)的左側(cè)分抗 F1與右側(cè)分抗 F2在相同運(yùn)算階下的極點(diǎn)頻率指數(shù)重合, 當(dāng)運(yùn)算階 μLiu=?0.5 時(shí),零點(diǎn)頻率指數(shù)也重合.時(shí), 零點(diǎn)頻率指數(shù)位置不同, 且運(yùn)算階為 μLiu( ? 0.5<μLiu<0 )時(shí),左側(cè)分抗 F1與右側(cè)分抗 F2的相鄰兩個(gè)零點(diǎn)頻率指數(shù)間距與運(yùn)算階為( ? 1 ?μLiu)時(shí)對(duì)應(yīng)的相鄰零點(diǎn)頻率指數(shù)間距近似相等.圖10(b)表明, 通過雙口網(wǎng)絡(luò)的左右側(cè)端口級(jí)聯(lián), 新的分抗的零極點(diǎn)頻率指數(shù)個(gè)數(shù)增加了一倍, 從而導(dǎo)致相鄰的零極點(diǎn)頻率指數(shù)間距變小.特別是當(dāng) μLiu=?0.5 時(shí), 相比于標(biāo)度分形格分抗, 相鄰零點(diǎn)與極點(diǎn)頻率指數(shù)間距減小了一半.因此, 級(jí)聯(lián)后的新網(wǎng)絡(luò)N 的分?jǐn)?shù)階運(yùn)算振蕩幅度大幅減小.

4.2 對(duì)稱格型級(jí)聯(lián)雙口網(wǎng)絡(luò)N 的電路優(yōu)化

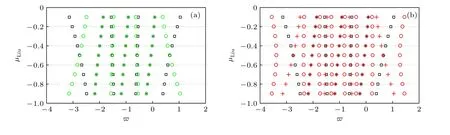
圖10 (a) 正比拓展左側(cè)分抗零極點(diǎn)指數(shù)(黑色)與右側(cè)分抗的零極點(diǎn)指數(shù)(綠色)分布對(duì)比圖; (b) 正比拓展左側(cè)分抗零極點(diǎn)指數(shù)(黑色)與新網(wǎng)絡(luò)N 的零極點(diǎn)指數(shù)(紅色)對(duì)比圖Fig.10.(a) The distribution comparison diagram of zero-pole exponents (black) of left-side fractance and zero-pole exponents(green) of right-side fractance in direct proportion extension; (b) the distribution comparison diagram of zero-pole exponents (black)of left-side fractance and zero-pole exponents (red) of new network N.

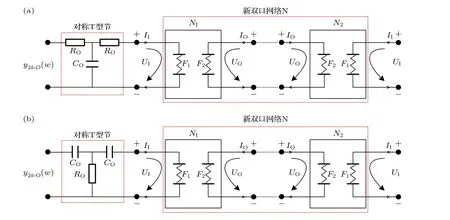
圖11 新雙口網(wǎng)絡(luò)N 的電路優(yōu)化原理圖 (a) 正比拓展優(yōu)化; (b) 反比拓展優(yōu)化Fig.11.Circuit optimization principle diagram of new two-port network N: (a) Optimization in direct proportion extension; (b) optimization in inverse proportion extension.

分析圖8 中對(duì)稱標(biāo)度格型級(jí)聯(lián)雙口網(wǎng)絡(luò)的運(yùn)算特征曲線, 在有效逼近頻段內(nèi), 當(dāng)頻率指數(shù)變量? →0時(shí), 分抗逼近電路的運(yùn)算特征曲線偏離理想分抗元的運(yùn)算特征直線.正比拓展時(shí), 有效逼近頻段內(nèi)較高頻率側(cè)的逼近效果有待優(yōu)化.當(dāng)運(yùn)算階?1<μLiu

結(jié)合分抗逼近電路的優(yōu)化理論及方法, 可以獲得高運(yùn)算恒定性和高逼近效益的任意階分抗逼近電路.對(duì)稱阻容T 型節(jié)是較為有效的分抗逼近電路優(yōu)化方法, 圖11 為級(jí)聯(lián)后的高運(yùn)算恒定性分抗的電路優(yōu)化原理圖.

由于格型級(jí)聯(lián)雙口網(wǎng)絡(luò)N 具有嚴(yán)格對(duì)稱性,右側(cè)端口分抗的優(yōu)化與左側(cè)相同.優(yōu)化原理圖中優(yōu)化元件的取值如(19)式, (19a)式為正比拓展時(shí)的電路優(yōu)化參數(shù), (19b)式為反比拓展優(yōu)化參數(shù).以階頻特征曲線為例, 正比拓展和反比拓展下優(yōu)化前后的新雙口網(wǎng)絡(luò)N 的運(yùn)算特征曲線對(duì)比如圖12,實(shí)驗(yàn)結(jié)果表明相頻特征曲線具有相同的優(yōu)化效果.

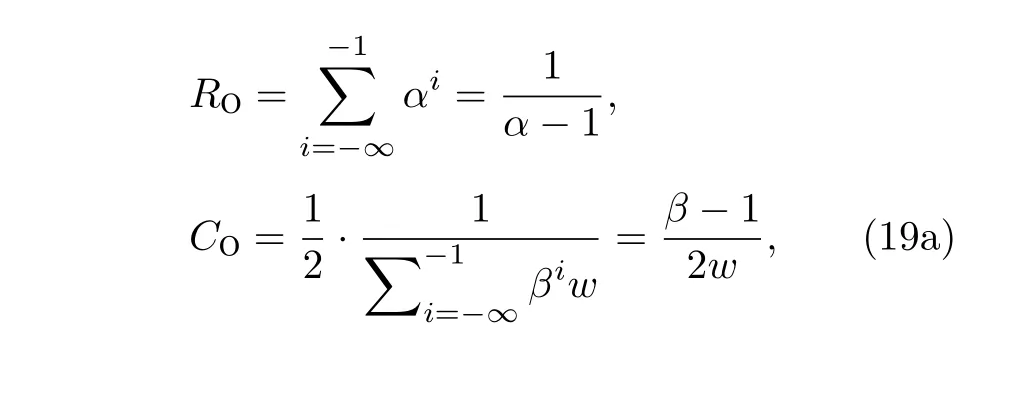
當(dāng)運(yùn)算階 μLiu=?0.5 時(shí), 級(jí)聯(lián)的低振幅分抗有效逼近帶寬最大, 此時(shí)不需優(yōu)化.當(dāng)運(yùn)算階μLiu?0.5 時(shí), 在頻率 w =1 附近(頻率指數(shù) ? =0 )運(yùn)算特征曲線偏離目標(biāo)運(yùn)算階的理想分抗頻域曲線, 此時(shí)優(yōu)化后的階頻特征曲線顯然比優(yōu)化前的新雙口網(wǎng)絡(luò)N 的階頻特征曲線具有更高的逼近效益.

5 實(shí)例應(yīng)用——信號(hào)的分?jǐn)?shù)階微分運(yùn)算

選用負(fù)半階對(duì)稱格型級(jí)聯(lián)雙口網(wǎng)絡(luò)N, 構(gòu)建半階微分運(yùn)算電路.取標(biāo)度因子 σ =5 , 運(yùn)算階μLiu=?0.5 , 由(7)式求解的標(biāo)度特征參量 α =β =2.2361.取電路節(jié)數(shù) k =5 , 電阻阻值 R =1 k? , 電容容值C =1 μF, 對(duì)稱格型級(jí)聯(lián)雙口網(wǎng)絡(luò)N 逼近的理想分抗元的阻抗值為

在Multisim14.0 中搭建模擬電路進(jìn)行仿真實(shí)驗(yàn),網(wǎng)絡(luò)N 模擬電路( 2 k =10,σ =5 )的頻域曲線與負(fù)半階標(biāo)度分形格分抗( k =5,σ =5 )及Carlson 原型分形格分抗( k =10 )的頻域曲線對(duì)比如圖13.

模擬電路的仿真結(jié)果與理論分析結(jié)果一致, 級(jí)聯(lián)后的對(duì)稱格型雙口網(wǎng)絡(luò)N 模擬電路的運(yùn)算振蕩幅度明顯減小.相同電路規(guī)模的Carlson 分形格分抗的相頻特征曲線也沒有運(yùn)算振蕩現(xiàn)象, 但有效逼近帶寬比網(wǎng)絡(luò)N 的小.設(shè)計(jì)的新網(wǎng)絡(luò)N 相對(duì)于標(biāo)度拓展前的Carlson 分形格電路, 獲得的拓展增益[26]

圖12 階頻特征曲線優(yōu)化對(duì)比圖 (a) 正比拓展優(yōu)化 ( k =8,σ =5 ); (b) 反比拓展優(yōu)化 ( k =8,σ =1/5 )Fig.12.Optimization comparison diagram of order-frequency characteristic curves: (a) Optimization in direct proportion extension( k =8,σ =5 ); (b) optimization in inverse proportion extension ( k =8,σ =1/5 ).

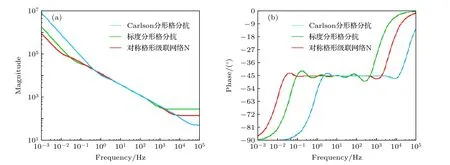
圖13 模擬電路仿真的頻域曲線對(duì)比圖 (a) 幅頻特征曲線; (b) 相頻特征曲線Fig.13.Frequency-domain curves comparison diagram of analog circuits: (a) Amplitude-frequency characteristic curves; (b) phasefrequency characteristic curves.

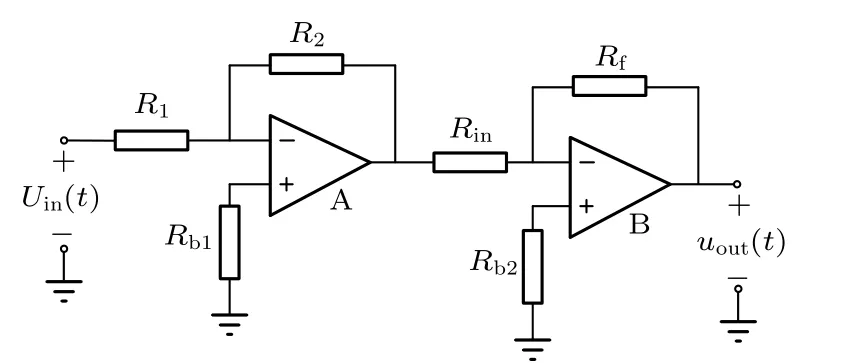
圖14 半階微分運(yùn)算電路原理圖Fig.14.Schematic diagram of half-order differential operational circuit.

使用頻域曲線如圖13 的新網(wǎng)絡(luò)N 作為理想分抗元F, 構(gòu)建半階微分運(yùn)算電路(圖14).其中R2=1 k? , Rf=10 k? , Rin=1 k? ,Rb1=Rb2=820 ? , R1使用 k =5 時(shí)的負(fù)半階新網(wǎng)絡(luò)N, 放大芯片A 和B 選擇Multisim14.0 中的運(yùn)算放大器OP37-AZ.該分?jǐn)?shù)階微分運(yùn)算電路的電壓傳輸函數(shù)為(22)式.

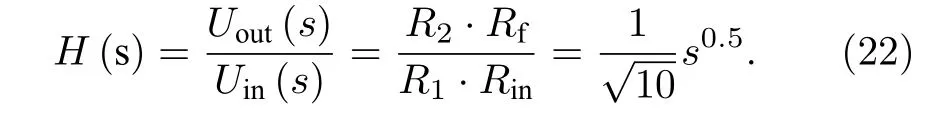
根據(jù)圖13 中的有效逼近頻率范圍, 選擇基波角頻率 ?0=1Hz , 峰峰值 E =0.5 V 的周期對(duì)稱方波為輸入信號(hào) uin(t).由周期對(duì)稱方波信號(hào)的半階微分運(yùn)算表達(dá)式

和半階微分運(yùn)算電路的電壓傳輸函數(shù)((22)式), 求解半階微分后的信號(hào) uout(t) 如圖15(a), Multisim14.0中模擬電路仿真的運(yùn)算結(jié)果如圖15(b).

分抗元也可用于構(gòu)建分?jǐn)?shù)階振蕩器, 使用k =5時(shí)的負(fù)半階新網(wǎng)絡(luò)N, 可設(shè)計(jì)分?jǐn)?shù)階維恩橋振蕩器.Multisim14.0 中的模擬負(fù)半階微分運(yùn)算電路仿真結(jié)果, 證實(shí)了設(shè)計(jì)的具有高運(yùn)算恒定性新網(wǎng)絡(luò)N 的有效性.

6 結(jié) 論

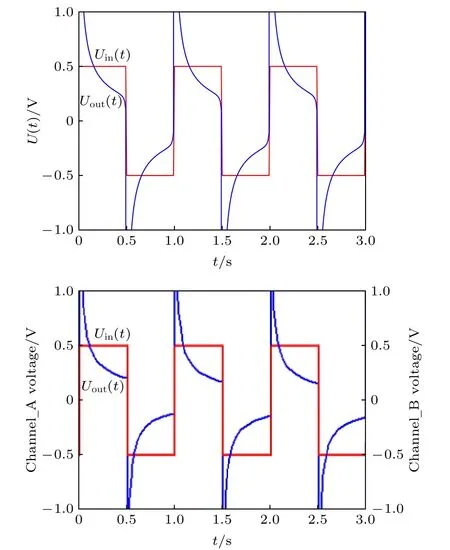
圖15 周期對(duì)稱方波的半階微分運(yùn)算 (a) 理論結(jié)果; (b) 模擬電路仿真結(jié)果Fig.15.The half-order differential operation of a periodic symmetrical square wave: (a) Theoretical result; (b) analog circuit simulation result.

本文提出一種實(shí)現(xiàn)具有高運(yùn)算恒定性分抗逼近電路的設(shè)計(jì)新方法.從電路網(wǎng)絡(luò)的角度分析經(jīng)典的標(biāo)度分形格分抗逼近電路, 發(fā)現(xiàn)該分抗的等效雙口網(wǎng)絡(luò)的兩側(cè)端口都可實(shí)現(xiàn)任意實(shí)數(shù)階理想分抗元的運(yùn)算性能.結(jié)合雙口網(wǎng)絡(luò)的傳輸參量矩陣, 構(gòu)造標(biāo)度拓展后的對(duì)稱格型級(jí)聯(lián)無(wú)源雙口網(wǎng)絡(luò), 并有效抑制了任意階標(biāo)度分形格分抗逼近電路的運(yùn)算振蕩現(xiàn)象.根據(jù)零極點(diǎn)頻率指數(shù)的分布情況, 理論分析任意階標(biāo)度分形格分抗運(yùn)算振蕩現(xiàn)象產(chǎn)生的原因, 從理論上分析抑制運(yùn)算振蕩幅度的方法.結(jié)合分抗逼近電路優(yōu)化理論, 實(shí)現(xiàn)具有恒定運(yùn)算性能、高逼近效益的任意分?jǐn)?shù)階格型級(jí)聯(lián)雙口網(wǎng)絡(luò).后續(xù)有待研究的問題是: 四類具有負(fù)半階運(yùn)算性能的Oldham 分形鏈類分抗逼近電路同樣具有恒定的運(yùn)算性能, 且同樣可等效為無(wú)源級(jí)聯(lián)雙口網(wǎng)絡(luò),因此, 是否可以構(gòu)造標(biāo)度拓展后鏈?zhǔn)浇Y(jié)構(gòu)的對(duì)稱級(jí)聯(lián)雙口網(wǎng)絡(luò), 這種結(jié)構(gòu)的分抗逼近電路是否也具有任意實(shí)數(shù)階恒定的運(yùn)算性能.