基于遺傳算法的甘肅省應急物流配送路徑優(yōu)化研究＊

馬麗榮，尹耀杰

(蘭州石化職業(yè)技術大學國際商務學院，甘肅 蘭州 730060)

近年來，甘肅遭受了多種自然災害，如地震、滑坡、山體崩塌、雪災、風雹、低溫冷凍、洪澇、干旱、泥石流等，特別是低溫冷凍、洪澇、風雹災害最為頻繁，也最為嚴重，各種自然災害給全省群眾生活及農牧業(yè)生產(chǎn)造成嚴重的影響。2020 年，自然災害共造成全省485.47 萬人次受災；因災遇難32 人、失蹤3 人；緊急轉移安置9.06 萬人；房屋倒塌3131戶、1.16 萬間，嚴重損壞9838戶、4.71 萬間，一般損壞2.92 萬戶、15.55 萬間；農作物受災396.33 千hm2，其中成災250.65 千hm2，絕收33.41 千hm2。直接經(jīng)濟損失約337.32 億元[1]。自然災害發(fā)生以后，提高政府部門對突發(fā)事件調控和應對能力，保證應急物資供應和市場價格基本穩(wěn)定帶來了巨大的挑戰(zhàn)，應急救援物資需要在有效的時間內輸送到災區(qū)，應急物資的快速供應直接關系到救援的成效。那么，災后應急物資如何及時有效的供應，應急物流設施如何定位，應急物流配送路徑如何規(guī)劃等等問題，是應急救災工作急需研究的課題。應急物流是應急管理系統(tǒng)的重要組成部分，主要承擔應急物資的儲備、運輸、配送及回收廢棄物的職責。

如何以最短路徑、高滿意度、最低成本等為目標在最短的時間內完成突發(fā)事件下應急物資的配送，已成為國內外學者高度關注的問題。李志等[2]研究了以物資分配公平性和需求效用最大化為目標，建立基于多目標的混合整數(shù)規(guī)劃方法應急物資供應點定位-分配模型；楊恩緣等[3]提出了以運輸成本最小為目標，結合容量限制及應急配送的多樣性和多級性特點，構建了應急物資多級配送選址-路徑的混合整數(shù)規(guī)劃模型；陳湉等[4]提出基于離散蜂群的災害應急物流車輛調度優(yōu)化問題研究，以供應過量、物資分配不足所造成的損失最小化、車輛調度成本最低為優(yōu)化目標，以服務時間窗和車輛運載能力為約束條件，構建了應急需求下的車輛調度優(yōu)化模型，并采用離散蜂群算法求解；張偉等[5]以運輸距離最短化、運輸時間最小化和路徑復雜性為目標，建立多目標應急物流路徑規(guī)劃模型；蔣杰輝[6]利用改進智能水滴算法求解應急物資配送中車輛路徑優(yōu)化問題；朱娜[7]采用“矢量投影－理想點法”以車輛運載能力等為限制條件，以應急運輸成本、應急時間及救災點數(shù)量為優(yōu)化目標構建了應急物資分配模型；朱佳翔[8]等以運輸時間最少、成本最優(yōu)以及用戶滿意度最大等為目標，構建多階段多目標應急物流配送的灰色動態(tài)規(guī)劃模型。

1 問題的描述

車輛運輸路徑問題（VRPTW）是應急物流研究的基本問題，也是實現(xiàn)在有限時間內實現(xiàn)物資的及時送達，提高救援效率，將災害降到最小化的有效途徑。文章針對甘肅應急物流運輸與配送問題，構建了以車輛數(shù)最少和路徑最短為目標的車輛配送模型，設計遺傳算法對應急物流配送路徑模型求解，兼顧考慮多個制約條件，如車輛載重量的限制，受災點對物資需求時間窗的限制等。假設有多個配送中心對多個受災點進行應急物資配送，配送中心有容量不同的車輛，受災點對物資需求的時間各不相同，要求在規(guī)定的時間內完成配送任務，規(guī)劃配送路線并要求每條路線上只有一輛車配送，規(guī)定車輛從配送中心出發(fā)完成配送任務后再返回配送中心，利用MATLAB 軟件編程求解，求出應急物流低成本高效率的配送路徑最優(yōu)解。

2 構建應急物流配送路徑模型

2.1 模型參數(shù)與變量定義

N={0，1，…，n，n+1}是節(jié)點集合，0,n+1 表示配送中心，需求點編號為{1，…，n}；

di：需求點i 的需求量；

K={1，2，…，k}是車輛集合；

A：弧的集合；

xijk={0，1}，表示車輛k 是否從i 點出發(fā)前往j點，如果車輛k 是從i 點出發(fā)前往j 點，則xijk=1，否則xijk=0；

Cij：表示i 點和j 點之間的距離；

wik：表示車輛k 對i 點的開始服務時間；

si：表示受災點i 的服務時間；

tij：表示從i 點到j 點的行駛時間；

Mij：一個足夠大的數(shù)，可以取10 的7 次方；

ai：受災點i 的左時間窗；

bi：受災點i 的右時間窗；

E：配送中心的左時間窗；

L：配送中心的右時間窗；

Ck：車輛k 最大裝載量；

s+(i)：表示從i 點出發(fā)的弧的集合；

s-(j)：表示回到j 點的弧的集合。

2.2 模型設計[9]

其中目標函數(shù)（1）表示車輛使用數(shù)目最少和車輛行駛總距離最短，將這兩個目標合為一個目標表示配送成本最低；（2）～（10）是約束條件，（2）表示每個需求點只能被分配到一條配送路徑上；（3）表示每條配送線路上從配送中心出發(fā)只能前往一個需求點；（4）表示車輛k 在路徑上的流量限制；（5）表示車輛配送完畢都必須返回配送中心；（6）表示配送時間連續(xù)性；（7）表示需求點時間窗約束；（8）表示配送中心時間窗約束；（9）表示載重量約束；（10）表示變量取值的約束。

3 基于遺傳算法（GA）的應急物流配送路徑模型求解

3.1 算法設計

3.1.1 編碼

在使用GA 求解VRPTW 問題時，可以采用整數(shù)編碼的形式對染色體進行編碼，當配送車輛數(shù)最多為K，且節(jié)點數(shù)目為N 時，染色體長度為N+K-1，那么表達該染色體的基本形式為（1，2，3，…，N，N+1，…，N+K-1）。

3.1.2 遺傳適應度函數(shù)

當編碼的解碼不能保證都滿足每條配送路線上對時間窗的約束和載重量的約束條件時，為了解決違反約束問題，那進行求解時采用懲罰函數(shù)。構建的懲罰函數(shù)如下：f(s)=c(s)+αq(s)+βw(s)，c(s)表示車輛總行駛距離，q(s)表示各條路徑違反的容量約束之和，w(s)表示所有顧客違反的時間窗約束之和。因為，違反容量約束相對來說不太容易，所以，將α 設為10，而較容易違反時間窗約束，所以，將β 設為100。

目標函數(shù)值越小越優(yōu)越，因此，在選擇環(huán)節(jié)，將懲罰函數(shù)的倒數(shù)設置為適應度函數(shù)，即為1/f(s)。

3.1.3 初始化種群

先構建帶時間窗車輛路徑問題的初始解，再進行初始化種群。

設節(jié)點數(shù)目為m。

第一步：任意選擇某一節(jié)點i∈{1，2，3，…，m}；

第二步：使用車輛數(shù)的初始化k=1；

第三步：遍歷節(jié)點生成序列Sq=[i，i+1，…，m，1，2，…，i-1]

第四步：遍歷節(jié)點j 至節(jié)點m，形成初始解。按序列Sq 遍歷節(jié)點Sq(j)，將節(jié)點Sq(j)添加到第q 條路徑中，在添加到對應線路中時要考慮車輛的載重量和左時間窗的約束條件。

得到的初始解就是一個配送方案，通過將個體賦值的方式轉換為種群初始化。

3.1.4 選擇

從群體中選擇優(yōu)良個體來繁殖子代的過程，并進行優(yōu)勝劣汰操作，通過基于適應度的過程選擇個體解決方案，即從群體中選擇多個適應度值大的個體進行交叉、變異以及局部搜索過程。

3.1.5 交叉

交叉是指新的個體由兩個父代個體的部分結構加以替換重組而生成的。

3.1.6 變異變異過程是指子代染色體由父代染色體的這兩個位置上的基因互換形成的。

3.1.7 終止條件

遺傳算法具有隨機搜索特性，需要設置終止條件，以在可接受時間內獲得最優(yōu)解。比如設置最大進化次數(shù)為終止條件，或達到最大迭代數(shù)時終止算法運算，再如判斷種群適應度值的收斂性，種群適應度值不被繼續(xù)優(yōu)化時終止算法運算。

3.2 遺傳算法的運算流程

遺傳算法（GA）是借鑒生物界的進化論，適者生存，優(yōu)勝劣汰的遺傳機制演化而來，是一種隨機化搜索全局尋優(yōu)的生物進化過程算法，具有內在的隱并行性和更好的全局尋優(yōu)能力，采用概率化的尋優(yōu)方法，能自動獲取和指導優(yōu)化的搜索空間，自適應地調整搜索方向，使群體不斷進化，逐漸接近最優(yōu)。GA 是解決VRPTW 問題的有效方法之一，在求解應急物流配送模型中得到了廣泛的應用[10]，如圖1所示。

圖1 遺傳算法流程圖

4 算例分析——以甘肅省定西漳縣和岷縣為例

甘肅省定西市漳縣和岷縣自古有“西控青海，南通巴蜀，東去三秦”之說，地處黃土梁峁地帶，山巒環(huán)抱，溝壑縱橫，是地震等自然災害高發(fā)地區(qū)，自然災害發(fā)生以后，災區(qū)需求大量的應急物資，由于災區(qū)地形地貌的特殊性，嚴重影響了對應急物資的配送，有必要在災區(qū)附件設置臨時的應急配送中心點，臨時應急配送中心負責為附近的鄉(xiāng)鎮(zhèn)配送應急物資。本文以定西市漳縣和岷縣為研究對象，兩縣共有31 個鄉(xiāng)鎮(zhèn)，利用奧維互動地圖查找到31 個鄉(xiāng)鎮(zhèn)的二維坐標經(jīng)度和維度，在模型計算中受災點的需求量是按照各鄉(xiāng)鎮(zhèn)人口數(shù)量、受災程度等信息估計得到，在考慮配送距離和受災點需求量的情況下構建應急物流選址模型，利用免疫算法優(yōu)化求解，采用MATLAB 軟件對設計進行編程實現(xiàn)，見表1。

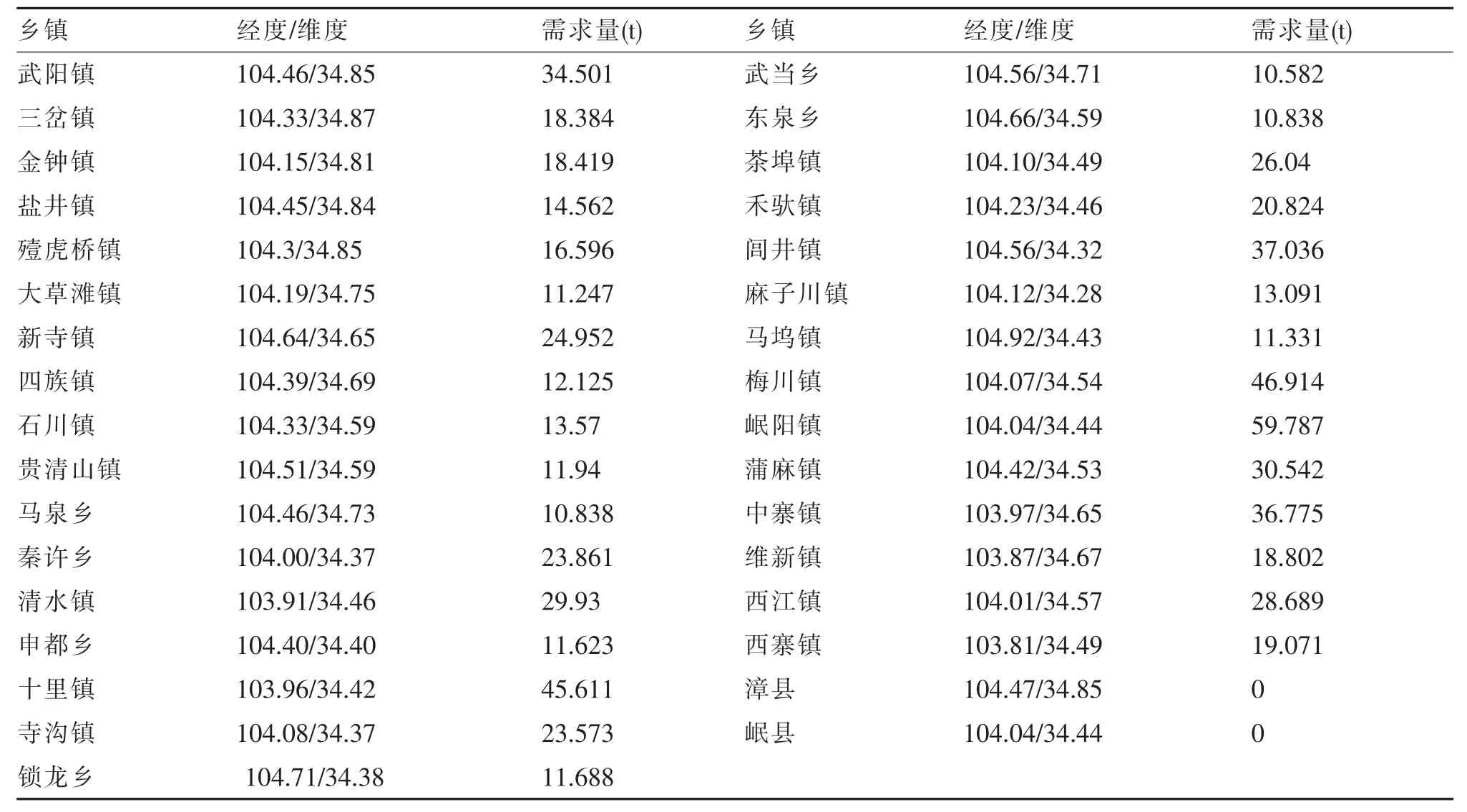
表1 甘肅省漳縣和岷縣各鄉(xiāng)鎮(zhèn)的數(shù)據(jù)資料

案例中，采用免疫算法確定了5 個鄉(xiāng)鎮(zhèn)為配送中心點，結果如圖2 所示。以這5 個配送中心點為出發(fā)點完成鄰近鄉(xiāng)鎮(zhèn)的配送路線規(guī)劃，采用MATLAB 軟件對設計的GA 算法進行編程實現(xiàn)，程序運行時間短，計算效率較高，有效實現(xiàn)了在規(guī)定的時間內應急物流配送路徑規(guī)劃。軟件求解結果如圖3 所示，最優(yōu)配送路徑見表2。

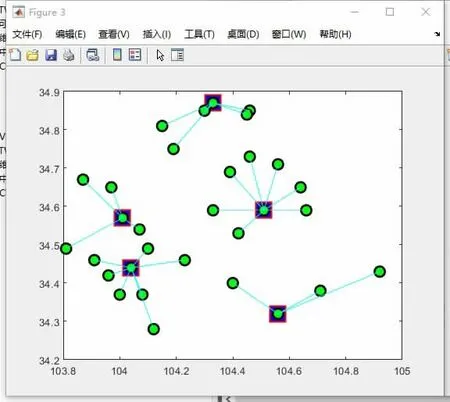
圖2 應急物流中心圖

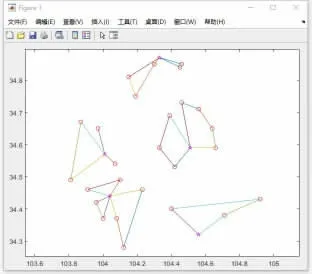
圖3 配送路徑優(yōu)化圖

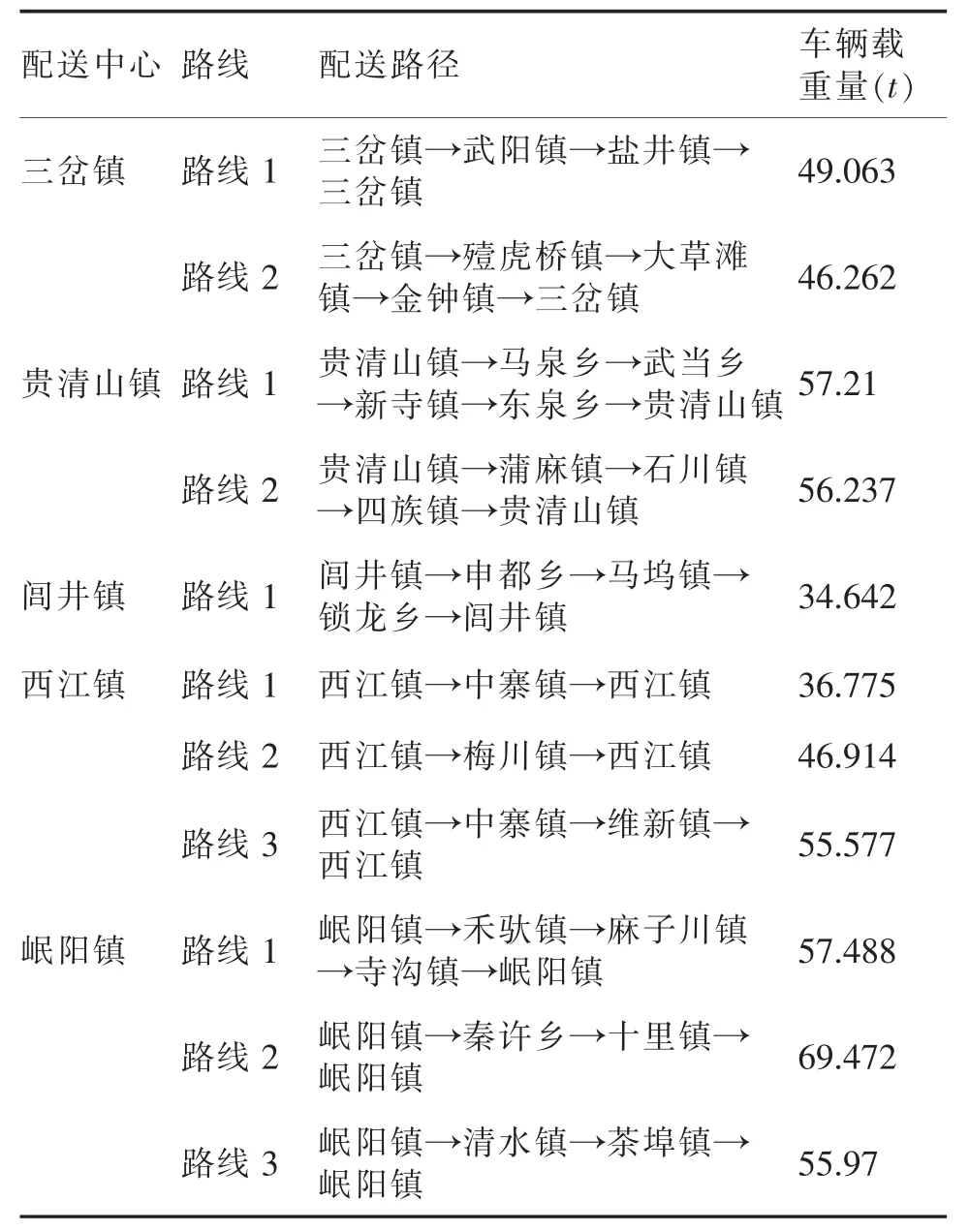
表2 多配送中心的配送路徑優(yōu)化結果

5 結語

文章針對配送中心如何向災區(qū)配送應急物資這一問題，提出了基于遺傳算法的應急物流車輛配送路徑優(yōu)化方案，構建了以車輛數(shù)最少和配送路徑最短為目標，綜合目標是以應急物流成本最低為目標，滿足多個約束條件下優(yōu)化問題模型，結合模型特點使用遺傳算法進行求解。研究結果表明，遺傳算法能有效的解決應急物流配送路徑問題，大大縮短應急配送時間，節(jié)約成本，提升滿意度，提高配送效率。