基于改進(jìn)變權(quán)-TOPISIS的錨固邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估

葉險(xiǎn)峰，韓以江，祝敕捷，程 雍

(湘潭大學(xué) 土木工程與力學(xué)學(xué)院，湖南 湘潭 411105)

0 引 言

工程邊坡穩(wěn)定是工程安全施工和運(yùn)營(yíng)的重要保障，對(duì)其進(jìn)行失穩(wěn)風(fēng)險(xiǎn)評(píng)估尤為重要。工程邊坡多為錨固邊坡，其失穩(wěn)風(fēng)險(xiǎn)受幾何尺寸形狀、巖土體類型和參數(shù)、周邊環(huán)境、加固結(jié)構(gòu)和施工擾動(dòng)等多因素綜合影響，且各影響因子難以準(zhǔn)確度量。監(jiān)測(cè)數(shù)據(jù)是邊坡穩(wěn)定情況的綜合體現(xiàn)，基于多期監(jiān)測(cè)資料的錨固邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估結(jié)果，可以有效反映，工程邊坡的穩(wěn)定情況及動(dòng)態(tài)變化規(guī)律[1-3]。在某監(jiān)測(cè)項(xiàng)目狀態(tài)很危險(xiǎn)且常權(quán)權(quán)重很低時(shí)，常權(quán)綜合結(jié)果通常顯示為該錨固邊坡依然安全，這會(huì)和實(shí)際情況不符，故筆者引入變權(quán)理論。

變權(quán)理論由WANG Peizhang率[4]先提出，李洪興[5]給出了變權(quán)理論和狀態(tài)變權(quán)向量的公理化定義，隨后又有大批學(xué)者對(duì)變權(quán)理論進(jìn)行豐富完善[6-9]。變權(quán)理論是根據(jù)指標(biāo)狀態(tài)間均衡水平，確定狀態(tài)變權(quán)向量進(jìn)而得到變權(quán)向量，調(diào)整各指標(biāo)在綜合決策中的效能，使得決策在指標(biāo)組狀態(tài)均衡的情況下進(jìn)行[10]。狀態(tài)變權(quán)向量通常由狀態(tài)變權(quán)函數(shù)代入變量得到，目前狀態(tài)變權(quán)函數(shù)多數(shù)是參照組態(tài)(指標(biāo)組狀態(tài))失衡程度、決策對(duì)象特性構(gòu)造的[7-12]，因此狀態(tài)變權(quán)函數(shù)對(duì)組態(tài)和決策對(duì)象具有針對(duì)性。當(dāng)決策對(duì)象包含多組組態(tài)失衡度相差較大的狀態(tài)值時(shí)(如多期變形監(jiān)測(cè)數(shù)據(jù))，各指標(biāo)組權(quán)重調(diào)節(jié)所需力度差別也較大，若使用多種狀態(tài)變權(quán)函數(shù)，構(gòu)造難度較大，若使用同種狀態(tài)變權(quán)函數(shù)，由于其組態(tài)失衡度針對(duì)性將可能導(dǎo)致誤用，使得變權(quán)調(diào)節(jié)度過(guò)大、過(guò)小或變權(quán)調(diào)節(jié)度與組態(tài)失衡度大小變化方向不一致的情況(如失衡度增大，而調(diào)節(jié)度減小)。

李德清等[6]提出用狀態(tài)向量離散度表示指標(biāo)組組態(tài)失衡度，在實(shí)際應(yīng)用中，當(dāng)狀態(tài)向量離散度相等時(shí)，其組態(tài)失衡度并不一定相等。假設(shè)在邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估中，2組監(jiān)測(cè)指標(biāo)狀態(tài)值分別為(0.5，0.6，0.7)、(0.8，0.9，1.0)，其離散度相等，設(shè)置“激懲平衡區(qū)間”相同，一般為區(qū)間(0，1)中較為居中位置的區(qū)間，顯然第2組各狀態(tài)值與“激懲平衡區(qū)間”邊界距離較大，其變權(quán)調(diào)節(jié)度會(huì)比第1組稍大，則組態(tài)失衡度也并不相等。

TOPISIS法(逼近理想解排序法)是按照各評(píng)估對(duì)象到理想化目標(biāo)的接近程度對(duì)有限評(píng)估對(duì)象進(jìn)行優(yōu)劣排序的方法，已應(yīng)用于諸多領(lǐng)域[13-16]，在邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估中也取得了良好效果[17]。

筆者提出一種基于指標(biāo)狀態(tài)到“激懲平衡區(qū)間”的距離的組態(tài)失衡度度量方案，構(gòu)造一種基于組態(tài)失衡度和狀態(tài)值的混合型狀態(tài)變權(quán)函數(shù)模型，并結(jié)合TOPISIS法，對(duì)錨固邊坡進(jìn)行基于多期監(jiān)測(cè)數(shù)據(jù)的失穩(wěn)風(fēng)險(xiǎn)評(píng)估。

1 變權(quán)原理及常權(quán)構(gòu)建

1.1 變權(quán)理論

為避免常權(quán)向量在多目標(biāo)決策問(wèn)題中因目標(biāo)組態(tài)不均衡而導(dǎo)致不合理綜合，文獻(xiàn)[4]提出變權(quán)理論，文獻(xiàn)[5]在其基礎(chǔ)上給出了變權(quán)向量、狀態(tài)變權(quán)向量等變權(quán)公理化定義，如下：

性質(zhì)2：連續(xù)性，即wi(x1,x2,…,xm)關(guān)于每一變?cè)B續(xù)；

性質(zhì)3：?jiǎn)握{(diào)性，即wi(x1,x2,…,xm)關(guān)于變?cè)獂i遞減(懲罰性變權(quán))或遞增(激勵(lì)性變權(quán))。

狀態(tài)變權(quán)向量定義：設(shè)Si:[0,1]→[0,1](i=1,2,…,m)，如果S(X)=(s(x1),s(x2),…,s(xm))滿足：

性質(zhì)1：?jiǎn)握{(diào)性，即對(duì)于任意X=(x1,x2,…,xm)∈[0,1]m，當(dāng)為懲罰變權(quán)時(shí)，若xi≥xj，則s(xi)≤s(xj)，當(dāng)為激勵(lì)變權(quán)時(shí)，若xi≥xj，則s(xi)≥s(xj)；

性質(zhì)2：連續(xù)性，即Si(x1,x2,…,xm)關(guān)于每一變?cè)B續(xù)；

(1)

1.2 常權(quán)權(quán)重向量構(gòu)建

確定權(quán)重方法眾多，常用有層次分析法、熵權(quán)法及組合賦權(quán)法等，筆者是對(duì)擁有多層次指標(biāo)體系的單個(gè)評(píng)估對(duì)象進(jìn)行風(fēng)險(xiǎn)評(píng)估，因此選擇較為簡(jiǎn)單的AHP賦權(quán)。鑒于AHP主觀性強(qiáng)的缺陷，一致性檢驗(yàn)過(guò)程復(fù)雜，筆者采用“三角模糊數(shù)”改進(jìn)的層次分析法確定指標(biāo)常權(quán)權(quán)重[18]，步驟如下：

1)一級(jí)指標(biāo)常權(quán)權(quán)重向量W*構(gòu)建。首先構(gòu)造三角模糊綜合判斷矩陣，并將其轉(zhuǎn)換為模糊判斷因子矩陣，再在其基礎(chǔ)上計(jì)算得到調(diào)整矩陣，然后對(duì)調(diào)整矩陣進(jìn)行相容變換，最后計(jì)算出一級(jí)指標(biāo)常權(quán)權(quán)重向量W*。

2)指標(biāo)常權(quán)權(quán)重向量Wo構(gòu)建

二級(jí)指標(biāo)的計(jì)算如式(2)：

(2)

式中：i=1，2，…，k，k為一級(jí)指標(biāo)個(gè)數(shù)；j=1,2，…，λ，j為某一級(jí)指標(biāo)下二級(jí)指標(biāo)個(gè)數(shù)；δ為某二級(jí)指標(biāo)常權(quán)權(quán)重占該一級(jí)指標(biāo)常權(quán)權(quán)重的比例系數(shù)，按照所在該一級(jí)指標(biāo)下二級(jí)指標(biāo)間的重要程度確定。

2 基于變權(quán)-TOPISIS法的評(píng)估模型

2.1 絕對(duì)理想方案標(biāo)準(zhǔn)化判斷矩陣

TOPISIS法是通過(guò)在樣本方案集內(nèi)部尋找理想解，并計(jì)算各方案與理想解的相對(duì)貼進(jìn)度，然后進(jìn)行優(yōu)劣排序的方法[16]。因此該方法多用于樣本方案集內(nèi)部排序，因樣本方案集決定的理想解通常只對(duì)樣本方案集有效，對(duì)其它樣本方案不一定成立。指標(biāo)評(píng)估等級(jí)標(biāo)準(zhǔn)閾值第一列和最后一列客觀上能代表評(píng)價(jià)目標(biāo)的最優(yōu)和最劣方案，筆者將其固定作為評(píng)估對(duì)象的絕對(duì)理想方案。

設(shè)包括指標(biāo)評(píng)估標(biāo)準(zhǔn)等級(jí)閾值方案在內(nèi)，共有n個(gè)決策方案，每個(gè)方案有m個(gè)指標(biāo)，指標(biāo)bij(其中i=1，2，…，m；j=1，2，…，n)為第j個(gè)方案的第i個(gè)評(píng)估指標(biāo)。則n個(gè)方案構(gòu)成的特征矩陣B如式(3)：

(3)

其中，第1列為負(fù)理想方案，第2～5列為指標(biāo)評(píng)級(jí)等級(jí)標(biāo)準(zhǔn)閾值方案，第n列為正理想方案。

方案指標(biāo)分為效益型(值越大越好)和成本型(值越小越好)兩類，為統(tǒng)一量綱，對(duì)判斷矩陣進(jìn)行標(biāo)準(zhǔn)化處理，得到標(biāo)準(zhǔn)化判斷矩陣C=(cij)m×n，即為評(píng)估值判斷矩陣，計(jì)算公式如式(4)、(5)：

對(duì)效益型指標(biāo)：

(4)

對(duì)成本型指標(biāo)：

(5)

正、負(fù)理想方案標(biāo)準(zhǔn)化即為絕對(duì)理想解，如式(6)：

(6)

2.2 組態(tài)失衡度

實(shí)際應(yīng)用中，由于激懲平衡區(qū)間的劃分，導(dǎo)致狀態(tài)值離散度無(wú)法準(zhǔn)確體現(xiàn)組態(tài)失衡度，筆者提出一種基于狀態(tài)值到激懲平衡區(qū)間邊界的距離的組態(tài)失衡度度量方案。

設(shè)qξ、qζ分別為低于懲罰水平、高于激勵(lì)水平值的指標(biāo)狀態(tài)值，(α，β)為評(píng)估對(duì)象指標(biāo)“激懲平衡區(qū)間”，τ為“激懲幅度比”(激勵(lì)與懲罰幅度的比值)，l、h分別為權(quán)重受懲罰、激勵(lì)的指標(biāo)個(gè)數(shù)，指標(biāo)組組態(tài)失衡度R計(jì)算如式(7)：

(7)

當(dāng)指標(biāo)狀態(tài)值不同時(shí)，式(7)中指標(biāo)組組態(tài)到“激懲平衡區(qū)間”邊界距離越大，R值越大，其組態(tài)失衡程度越大，各指標(biāo)權(quán)重所需調(diào)節(jié)力度越大，和實(shí)際情況相符；當(dāng)指標(biāo)狀態(tài)值相同時(shí)，無(wú)論R值大小，狀態(tài)變權(quán)函數(shù)值相等，各指標(biāo)權(quán)重所需調(diào)節(jié)力度相等，等效于調(diào)節(jié)度為0，和實(shí)際情況亦相符。

2.3 狀態(tài)變權(quán)函數(shù)的構(gòu)造及變權(quán)權(quán)重

針對(duì)已有狀態(tài)變權(quán)函數(shù)，在決策對(duì)象包含多組組態(tài)失衡度相差較大的狀態(tài)值組，這一情況下適用性較低的問(wèn)題，筆者構(gòu)造一種包含組態(tài)失衡度的混合型狀態(tài)變權(quán)函數(shù)，如式(8)：

(8)

式中：R為指標(biāo)組組態(tài)失衡度；xi為指標(biāo)i的狀態(tài)值；m為指標(biāo)組指標(biāo)個(gè)數(shù)；τ為“激懲幅度比”；α、β分別為懲罰和激勵(lì)的指標(biāo)狀態(tài)臨界值，(0，α)為懲罰區(qū)，[α，β]為“激懲平衡區(qū)間”，(β，1]為激勵(lì)區(qū)，其中α、β、τ由專家建議確定。

經(jīng)驗(yàn)證，式(8)滿足文獻(xiàn)[5]給出的變權(quán)公理中的各性質(zhì)，同時(shí)滿足提升對(duì)極端指標(biāo)關(guān)注度、激勵(lì)幅度小于懲罰幅度、不能脫離常權(quán)限制等要求[11]。

最后，結(jié)合式(2)～式(7)計(jì)算常權(quán)向量Wo及狀態(tài)變權(quán)向量S(X)，代入公式(1)，可得最終變權(quán)向量W(X)。

2.4 計(jì)算各方案的評(píng)估結(jié)果

2.4.1 加權(quán)標(biāo)準(zhǔn)化決策矩陣

對(duì)標(biāo)準(zhǔn)化判斷矩陣C=(cij)m×n中第μ個(gè)方案標(biāo)準(zhǔn)化數(shù)據(jù)和理想解賦權(quán)(η=2，3，…，n-1)，理想方案標(biāo)準(zhǔn)化后為標(biāo)準(zhǔn)化決策矩陣的第1列和最后一列，得到判斷矩陣Tμ：

(9)

2.4.2 各方案到絕對(duì)理想方案的相對(duì)貼近度

相對(duì)貼近度可以用歐式距離來(lái)度量，表示為E，第個(gè)η方案的相對(duì)貼近度Eη：

(10)

(11)

在邊坡失穩(wěn)風(fēng)險(xiǎn)概率評(píng)估中，Eη即為第η個(gè)方案的失穩(wěn)風(fēng)險(xiǎn)概率值。

3 案例應(yīng)用及分析

筆者以燈盞塢隧道進(jìn)口端洞頂仰坡為例，進(jìn)行錨固邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估。該邊坡地質(zhì)構(gòu)造復(fù)雜，且有仰坡順層，整體地下水不發(fā)育，主要加固措施為錨固樁和錨索框架梁。為確保工程施工和運(yùn)營(yíng)安全，從位移和應(yīng)力兩方面，對(duì)邊坡進(jìn)行框架梁上表面的坡頂表面位移、深部位移、錨固樁樁頂水平位移、錨索框架梁錨索拉力、框架梁與土接觸面壓力、樁側(cè)土壓力等跟蹤監(jiān)測(cè)，頻率為5 d/次，并進(jìn)行邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估，如圖1。

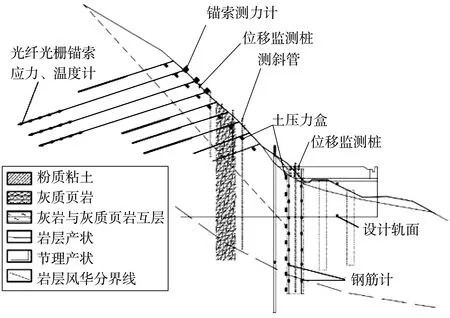
圖1 邊坡監(jiān)測(cè)元件分布剖面

3.1 錨固邊坡失穩(wěn)風(fēng)險(xiǎn)性評(píng)估體系

在遵循典型性、獨(dú)立性、層次性、可靠性、可量化等指標(biāo)選取的原則之下，選取指標(biāo)如表1。由于該錨固邊坡地下水不發(fā)育，對(duì)穩(wěn)定性影響較小，同時(shí)由于該項(xiàng)目沒(méi)有地表裂縫監(jiān)測(cè)項(xiàng)，地表裂縫被施工殘?jiān)傲锷痴趽酰瑔慰咳斯ぱ惨暉o(wú)法確定其準(zhǔn)確情況，此處未選取地下水位指標(biāo)和地表裂縫指標(biāo)。

表1 風(fēng)險(xiǎn)評(píng)估指標(biāo)體系

3.2 各監(jiān)測(cè)項(xiàng)目風(fēng)險(xiǎn)等級(jí)

筆者將邊坡失穩(wěn)風(fēng)險(xiǎn)劃分為5個(gè)等級(jí)，對(duì)應(yīng)的評(píng)語(yǔ)集V={Ⅰ級(jí),Ⅱ級(jí),Ⅲ級(jí),Ⅳ級(jí),Ⅴ級(jí)}={安全狀態(tài),跟蹤狀態(tài),預(yù)警狀態(tài),報(bào)警狀態(tài),危險(xiǎn)狀態(tài)}，則評(píng)判指標(biāo)i也劃分為5個(gè)等級(jí)標(biāo)準(zhǔn)區(qū)間，并以各個(gè)監(jiān)測(cè)項(xiàng)目規(guī)范或設(shè)計(jì)文件規(guī)定的各項(xiàng)形變?cè)O(shè)計(jì)允許值為基準(zhǔn)，考慮到設(shè)計(jì)較為保守，以設(shè)計(jì)允許值的60%、90%、110%、120%、125%對(duì)形變累計(jì)指標(biāo)進(jìn)行分級(jí)，以設(shè)計(jì)允許值的50%、80%、100%、110%、115%對(duì)速率指標(biāo)進(jìn)行分級(jí)[19-20]，具體如表2。

表2 指標(biāo)評(píng)估等級(jí)標(biāo)準(zhǔn)劃分

3.3 指標(biāo)變形監(jiān)測(cè)數(shù)據(jù)

筆者以累計(jì)形變量最大監(jiān)測(cè)點(diǎn)量測(cè)數(shù)據(jù)作為指標(biāo)數(shù)據(jù)。該隧道進(jìn)口2018年4月27日上臺(tái)階開挖，2018年5月31日隧道上臺(tái)階約開挖30 m，2018年6月30日隧道開挖約65 m，2018年7月31日隧道開挖約80 m，2018年7月5日完成明洞仰拱、洞口管棚支護(hù)，此過(guò)程中，隧道開挖對(duì)邊坡的擾動(dòng)從逐漸增大到逐漸降低到可忽略，且該邊坡受其它因素影響較小，因此5、6、7月是該邊坡失穩(wěn)風(fēng)險(xiǎn)高峰期，對(duì)其進(jìn)行評(píng)估則可以把握該邊坡失穩(wěn)風(fēng)險(xiǎn)變化情況及未來(lái)邊坡穩(wěn)定情況，對(duì)該3個(gè)月監(jiān)測(cè)數(shù)據(jù)平均每半個(gè)月進(jìn)行一次評(píng)估，各指標(biāo)監(jiān)測(cè)數(shù)據(jù)數(shù)值如表3。

表3 各指標(biāo)各期監(jiān)測(cè)數(shù)值

3.4 錨固邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估

1)常權(quán)權(quán)重的確定

筆者邀請(qǐng)到5位專家分別運(yùn)用“1～9標(biāo)度法”對(duì)各指標(biāo)權(quán)重三角模糊打分，計(jì)算得到一級(jí)常權(quán)權(quán)重：W*=(0.219,0.148,0.194,0.088,0.063,0.165,0.123)。由于采用最大變形速率比采用最大變形值來(lái)判斷評(píng)估變形體的失穩(wěn)風(fēng)險(xiǎn)更加準(zhǔn)確[21]，故確定W累計(jì)形變∶W變形速率=2∶3，即δ1=0.4，δ2=0.6，最終得到常權(quán)權(quán)重，如表4。

2)變權(quán)權(quán)重的確定

首先由指標(biāo)評(píng)估等級(jí)標(biāo)準(zhǔn)劃分閾值和各期指標(biāo)監(jiān)測(cè)數(shù)值構(gòu)造初始判斷矩陣，并進(jìn)行標(biāo)準(zhǔn)化，得到指標(biāo)監(jiān)測(cè)值標(biāo)準(zhǔn)化判斷矩陣C，即指標(biāo)狀態(tài)值；經(jīng)狀態(tài)變權(quán)模型，計(jì)算得到各評(píng)估方案樣本的組態(tài)失衡度R及變權(quán)向量，其中α=0.3，β=0.7，τ=0.8，具體結(jié)果見表4。為方便對(duì)比分析，增加常權(quán)權(quán)重，

表4 各方案樣本變權(quán)權(quán)重

參考文獻(xiàn)[6]中變權(quán)調(diào)節(jié)度的算法,以狀態(tài)變權(quán)函數(shù)與1的偏差絕對(duì)值的均值之和除以狀態(tài)值在“激勵(lì)平衡區(qū)間”之外的指標(biāo)個(gè)數(shù)得到變權(quán)調(diào)節(jié)度F1。

3)評(píng)估結(jié)果計(jì)算

由矩陣C和表4中各方案變權(quán)向量，得到各方案貼近度E，即邊坡失穩(wěn)風(fēng)險(xiǎn)概率值。為驗(yàn)證筆者評(píng)估模型的優(yōu)越性，增加常權(quán)、文獻(xiàn)[11]中具有代表性的混合型狀態(tài)變權(quán)函數(shù)與TOPISIS法結(jié)合的評(píng)估模型作對(duì)比，其中參數(shù)取值與筆者相同，變權(quán)調(diào)節(jié)度F2見表4，變權(quán)評(píng)估結(jié)果見表5。

表5 各評(píng)估模型評(píng)估結(jié)果

3.5 結(jié)果分析

1)狀態(tài)變權(quán)結(jié)果分析

部分監(jiān)測(cè)和閾值方案各指標(biāo)變權(quán)權(quán)重與常權(quán)權(quán)重對(duì)比情況，如圖2。由圖2可知，閾值樣本各指標(biāo)變權(quán)權(quán)重與常權(quán)基本相等，而監(jiān)測(cè)樣本各指標(biāo)變權(quán)權(quán)重與常權(quán)偏差較為明顯。筆者各指標(biāo)閾值按各設(shè)計(jì)允許值等比設(shè)置，且各對(duì)應(yīng)等級(jí)間比例較為接近，其組態(tài)較為均衡，各閾值方案權(quán)重基本無(wú)需調(diào)整，監(jiān)測(cè)數(shù)據(jù)樣本各指標(biāo)狀態(tài)相差較大，需進(jìn)行權(quán)重調(diào)整，而圖2中閾值樣本權(quán)重變化情況與理論相符，這證明筆者變權(quán)模型具有合理性。

圖2 變權(quán)與常權(quán)權(quán)重對(duì)比

將表4中各評(píng)價(jià)等級(jí)閾值方案及各期監(jiān)測(cè)數(shù)據(jù)方案對(duì)應(yīng)的兩種變權(quán)函數(shù)的變權(quán)調(diào)節(jié)度F1、F2,與組態(tài)失衡度R繪制成圖3。由圖3可見，各方案的指標(biāo)組組態(tài)失衡度大小順序?yàn)椤伴撝?<閾值3<5/16<6/28<6/15<7/13<5/02<7/29<閾值4<5/31<閾值5”，按文獻(xiàn)[12]中狀態(tài)變權(quán)函數(shù)模型求得的變權(quán)調(diào)節(jié)度大小順序?yàn)椤伴撝?<閾值3<6/28<5/16<5/02<6/15<閾值4<7/13<5/31<7/29<閾值5”，筆者中狀態(tài)變權(quán)函數(shù)模型求得的變權(quán)調(diào)節(jié)度大小順序?yàn)椤伴撝?<閾值3< 5/16<6/28<6/15<7/13<5/02<7/29<閾值4<5/31<閾值5”。由文獻(xiàn)[4]～[9]可知，指標(biāo)組組態(tài)失衡程度越大，權(quán)重所需調(diào)節(jié)度越大。按文獻(xiàn)[11]中的狀態(tài)變權(quán)函數(shù)得到變權(quán)調(diào)節(jié)度并未隨組態(tài)失衡度增大而嚴(yán)格增大，筆者包含組態(tài)失衡度的狀態(tài)變權(quán)函數(shù)得到的狀態(tài)變權(quán)向量嚴(yán)格滿足這一要求，這證明筆者的變權(quán)模型更優(yōu)越。

圖3 狀態(tài)變權(quán)調(diào)節(jié)度分析

2)案例錨固邊坡失穩(wěn)風(fēng)險(xiǎn)分析

對(duì)比3種評(píng)估模型綜合評(píng)估結(jié)果，如圖4。在風(fēng)險(xiǎn)等級(jí)方面，3者得到的等級(jí)閾值完全一致，其中7月13日和7月29日變權(quán)評(píng)估模型得到的風(fēng)險(xiǎn)等級(jí)比常權(quán)高一級(jí)；在風(fēng)險(xiǎn)評(píng)估數(shù)值方面，變權(quán)方模型比常權(quán)評(píng)估模型得到的各期監(jiān)測(cè)數(shù)據(jù)的失穩(wěn)風(fēng)險(xiǎn)值整體偏大，3者評(píng)估結(jié)果值變化趨勢(shì)相同，其中2種變權(quán)評(píng)估模型得到的失穩(wěn)風(fēng)險(xiǎn)峰值都較常權(quán)評(píng)估模型提前了5天左右，且2種變權(quán)評(píng)估方案得到的風(fēng)險(xiǎn)值和風(fēng)險(xiǎn)等級(jí)都具有高度的相似性。綜上可知，筆者變權(quán)模型科學(xué)合理，同時(shí)在錨固邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估中，變權(quán)評(píng)估模型優(yōu)于常權(quán)評(píng)估模型。

圖4 各評(píng)估模型結(jié)果對(duì)比

如圖4，筆者變權(quán)模型得到的錨固邊坡失穩(wěn)風(fēng)險(xiǎn)峰值及失穩(wěn)風(fēng)險(xiǎn)較小值都比文獻(xiàn)變權(quán)評(píng)估模型得到的結(jié)果大，失穩(wěn)風(fēng)險(xiǎn)程度一般的結(jié)果相對(duì)較小。在混合變權(quán)模型在風(fēng)險(xiǎn)偏好類的評(píng)估中，權(quán)重調(diào)整通常會(huì)使得評(píng)估結(jié)果更傾向于負(fù)面，因?yàn)樗鼘顟B(tài)較為惡劣的指標(biāo)權(quán)重調(diào)大，將狀態(tài)較優(yōu)的指標(biāo)權(quán)重調(diào)小，以常權(quán)評(píng)估結(jié)果作為參照，權(quán)重調(diào)節(jié)力度越大評(píng)價(jià)結(jié)果增大越明顯。結(jié)合圖3可知，筆者的變權(quán)模型在組態(tài)失衡程度較大時(shí)，權(quán)重調(diào)整力度較大，組態(tài)失衡程度較小時(shí)，權(quán)重調(diào)整力度較小，而2種變權(quán)評(píng)估模型設(shè)置的參數(shù)大小相同，這說(shuō)明筆者變權(quán)模型，相較對(duì)比模型對(duì)狀態(tài)較為極端的指標(biāo)敏感性較高，較均衡的狀態(tài)值敏感性較低，這更符合變權(quán)混合變權(quán)模型的要求“提升對(duì)極端指標(biāo)的關(guān)注度”。因此，在錨固邊坡的失穩(wěn)風(fēng)險(xiǎn)評(píng)估中，筆者變權(quán)模型優(yōu)于對(duì)比變權(quán)模型。

分析筆者變權(quán)評(píng)估模型綜合評(píng)估結(jié)果可知，該案例錨固邊坡失穩(wěn)風(fēng)險(xiǎn)概率值從5月2日至6月10日左右不斷增大，從6月10日左右至7月10日左右，不斷減小，從7月10日至7月29日緩慢變化。5月2日至5月13日左右，該錨固邊坡失穩(wěn)風(fēng)險(xiǎn)等級(jí)為“Ⅰ級(jí)”，風(fēng)險(xiǎn)狀態(tài)為“安全狀態(tài)”。5月13日左右至7月29日，該錨固邊坡失穩(wěn)風(fēng)險(xiǎn)等級(jí)為“Ⅱ級(jí)”，風(fēng)險(xiǎn)狀態(tài)為“跟蹤狀態(tài)”。

結(jié)合工程施工進(jìn)展分析，該隧道口錨固邊坡于2018年4月27日開挖，開挖之初，由于洞口管棚和明洞仰拱支護(hù)施工未完成，加之開挖施工擾動(dòng)，邊坡應(yīng)力釋放，進(jìn)行表生改造和應(yīng)力場(chǎng)調(diào)整，應(yīng)力和位移變形加快，使得邊坡失穩(wěn)風(fēng)險(xiǎn)概率升高；6月初，開挖超過(guò)30m，超出了坡面里程范圍，隨著邊坡下方施工的繼續(xù)進(jìn)行，其施工擾動(dòng)逐漸減小，邊坡應(yīng)力場(chǎng)逐漸轉(zhuǎn)化為自重應(yīng)力場(chǎng)為主，邊坡應(yīng)力和位移減緩，其失穩(wěn)風(fēng)險(xiǎn)概率降低；7月10日，隨著洞口管棚、明洞仰拱支護(hù)的完成和施工開挖深入，支護(hù)達(dá)到飽和狀態(tài)，坡體下滑力和支撐力達(dá)到平衡，錨固邊坡整體上逐漸趨于穩(wěn)定。綜上可知，所得評(píng)估結(jié)果與該錨固邊坡實(shí)際情況完全相符，證明筆者變權(quán)評(píng)估模型適用于錨固邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估。由于該錨固邊坡今后所受工程擾動(dòng)較小，且處于地震低發(fā)地帶，地下水不發(fā)育，其負(fù)面影響因素較少，加固設(shè)施完備，故可判定之后該錨固邊坡失穩(wěn)風(fēng)險(xiǎn)等級(jí)將不高于“Ⅱ級(jí)”，即“跟蹤狀態(tài)”，較為安全。

4 結(jié) 論

1)在實(shí)際應(yīng)用中，基于指標(biāo)狀態(tài)到“激懲平衡區(qū)間”的距離的組態(tài)失衡度能較好的體現(xiàn)指標(biāo)組態(tài)失衡情況。

2)包含組態(tài)失衡度的狀態(tài)變權(quán)函數(shù)模型，在決策評(píng)估對(duì)象包含多組組態(tài)失衡度相差較大的狀態(tài)值時(shí)，得到的變權(quán)調(diào)節(jié)度依然滿足“指標(biāo)組狀態(tài)失衡程度越大，變權(quán)調(diào)節(jié)度越大”的要求，即適用性更高，同時(shí)其對(duì)優(yōu)勢(shì)和劣勢(shì)狀態(tài)敏感度更高，對(duì)較平衡的狀態(tài)敏感度更低，效果更好。

3)筆者變權(quán)理論與TOPISIS法結(jié)合的評(píng)估模型能較好的適用于錨固邊坡失穩(wěn)風(fēng)險(xiǎn)評(píng)估。

4)2種變權(quán)與常權(quán)評(píng)估結(jié)果對(duì)比，驗(yàn)證了變權(quán)評(píng)估模型對(duì)優(yōu)勢(shì)和劣勢(shì)狀態(tài)指標(biāo)更敏感，優(yōu)于常權(quán)評(píng)估模型。