軸流轉槳式水輪機協聯關閉規律選擇及優化分析

王 苗，張小瑩，周天馳，張曉煒

(1.新疆農業職業技術學院，新疆 昌吉 831100；2.新疆農業大學水利與土木工程學院，烏魯木齊 830052；3.中國電建集團華東勘測設計研究院，杭州 310000)

0 引 言

由于地形地質條件的限制，很多水電站常常采用明渠結合有壓管道的引水系統布置形式，這在中小型電站中尤為常見[1]，此類電站又稱無壓引水式電站。為了滿足上游河道的灌溉要求或者通航要求，無壓引水式電站引水明渠的水位和流量變化往往較大，一般定槳式機組的高效區難以涵蓋較大的水頭區間，因此此類電站通常安裝軸流轉槳式水輪機，以利用不同水頭和流量組合，提高發電效率[2]。

與混流式水輪機或者軸流定漿式水輪機相比，軸流轉槳式水輪機的槳葉和導葉能隨著水頭和流量的變化而相應的開大或者關小，保證機組一直運行在高效率區，提高發電量。但是當電站發生甩負荷時，由于槳葉調節的存在，其關閉方式與定槳式水輪機有所不同：槳角開度變化的存在相當于關閉規律多了一個維度。所以無論是關閉規律選擇還是優化方面，采用軸流轉槳式機組的水電站水力過渡過程計算都較定槳式復雜。

近些年，國內許多學者在軸流轉槳式水輪機過渡過程方面做了很多研究[3-5]，在特性曲線處理方面，張蓉生[6]分析了傳統幾何方法處理綜合特性曲線的二重性，引入德洛內三角網剖分方法對數據插值，該方法能夠較好地處理轉槳式機組的協聯曲線。在軸向水推力方面，彭小東[7]給出了采用軸流式機組的水電站在過渡過程計算中應當注意的問題，討論了軸流轉槳式機組的蝸殼長度直徑當量計算的方法以及軸流式機組的力矩、流量和軸向水推力的仿真計算方法。目前對其關閉規律的選擇和優化方面研究較少，而在水電站調節保證計算中，合適的導葉-槳葉動作方式可以起到改善蝸殼壓力、降低機組轉速、減小軸向抬機力的作用，這是一種低成本而又高效的優化手段。

本文通過理論分析轉槳式水輪機的協聯飛逸曲線，結合實際工程實例，分別使用槳葉關閉、槳葉不動以及槳葉開啟的動作規律(3種動作規律中導葉均一段直線關閉)，計算甩負荷時蝸殼末端壓力和機組轉速上升率，據此選擇合適的槳葉動作方式。在確定電站甩負荷時槳葉動作方式之后，采用可以用于多控制工況的導葉關閉規律優化非線性模型，運用模擬退火算法優化轉槳式水輪機導葉的兩段折線關閉規律，最后得到較優的導葉槳葉協聯關閉規律。

1 協聯關閉規律選擇

1.1 理論分析

安裝混流式機組的水電站發生甩負荷過渡過程時，導葉動作方式有一段直線關閉、兩段直線關閉[8](先快后慢應用于低比轉速水輪機，先慢關后快關應用于高比轉速水輪機)、多段直線關閉[9]等；安裝可逆式機組的抽水蓄能電站中，除了以上關閉規律之外，還有先延遲再直線關閉的關閉規律[10]，其原因主要是考慮了可逆式機組S區的反水泵效應。總而言之，水電站導葉關閉規律的選擇應該根據電站布置情況和水輪機特性進行綜合考慮和具體分析。

轉槳式水輪機的槳葉和導葉均可動作，由于槳葉調節的加入，轉槳式水輪機的甩負荷過渡過程與常規定槳式差別較大，所以其關閉規律選擇較為復雜。一般工程中發生甩負荷時，機組常用的關閉規律是在機組導葉快速關閉以快速削減水流，而槳葉也同時緩慢關閉。下面通過分析轉槳式水輪機的協聯飛逸曲線圖，從理論上選擇適合軸流轉槳式機組的較優導葉-槳葉動作方式。

圖1中為某軸流轉槳式水輪機的協聯飛逸曲線圖，圖1中實線為槳葉開度線，從左到右依次增大，而虛線為導葉開度線，從下到上依次增大。分析如下：對于同樣的導葉開度，槳葉開啟的越大時，水輪機的飛逸轉速越低；對于同樣的槳葉開度，導葉開啟的越大時，水輪機的飛逸轉速越高。所以在甩負荷過渡過程中，若導葉關閉的同時，槳葉快速開啟，在導葉完全關閉之前，槳葉開度達到最大值，機組最大轉速上升率將會降低。

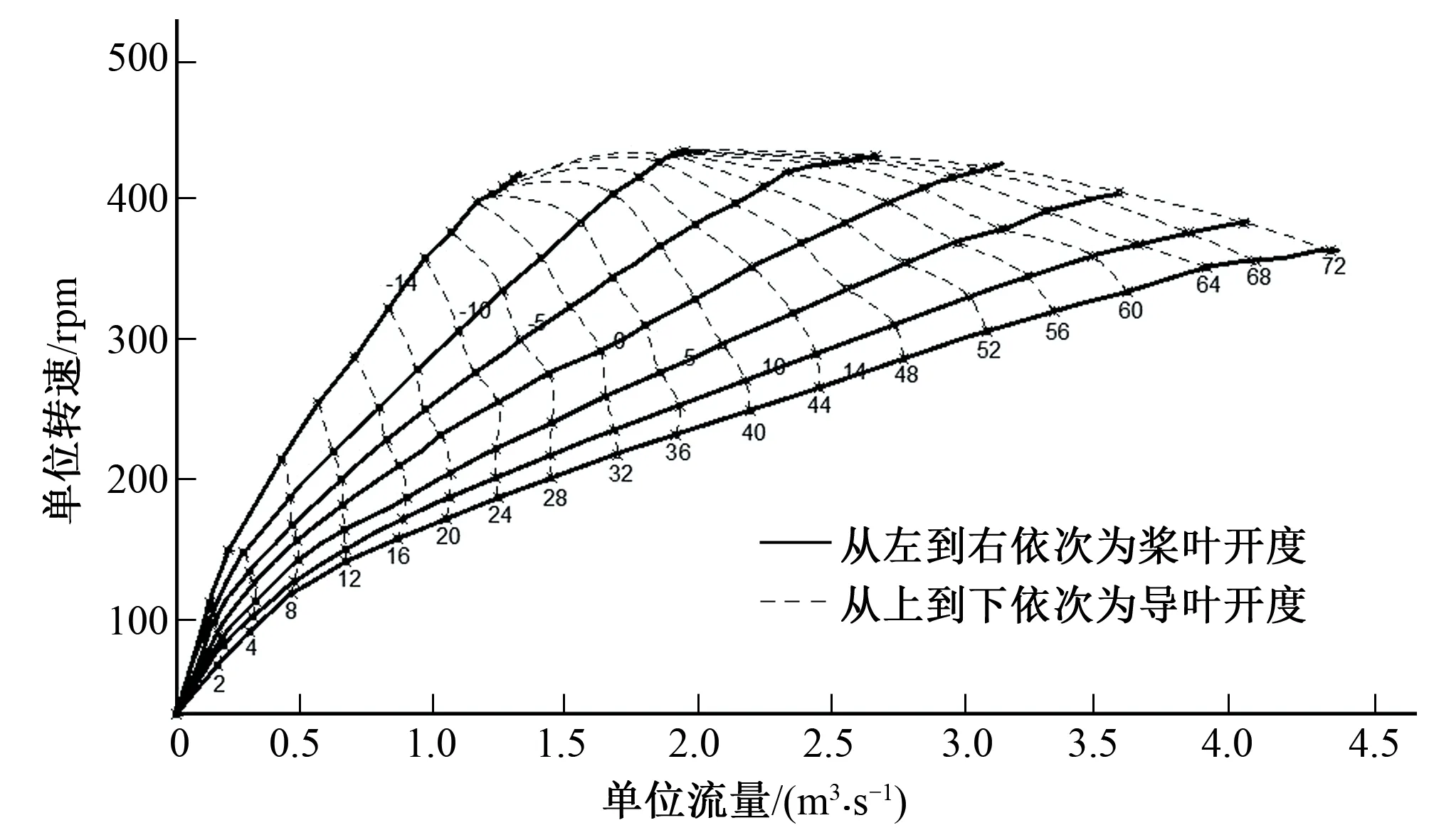
圖1 某軸流轉槳式水輪機的協聯飛逸曲線圖Fig.1 Runaway curve of a Kaplan turbine

根據上述分析，可以對轉槳式水輪機提出一種新的關閉規律：當電站發生甩負荷時，導葉一段直線或者兩段直線快速關閉，槳葉一段直線開速開啟。由軸流轉槳式水輪機的特點可知，這種關閉規律能夠大大降低甩負荷過程中的機組轉速和水錘壓力。為了驗證以上分析的正確性，采用特征線法[11]，基于某一工程實例進行甩負荷過渡過程數值仿真計算。

1.2 實例驗證

基本資料：某明渠引水式水電站裝有3臺卡普蘭式(軸流轉槳)水輪機，總裝機140 MW，采用單管單機的布置形式，水輪機的額定水頭22.5 m，額定流量227.5 m3/s，額定轉速125 r/min，額定出力48.11 MW。輸水系統包括引水明渠、前池、壓力鋼管、尾水管、尾水池、尾水明渠等。其中引水渠長約560 m，寬40～150 m，尾水渠長約382 m，寬90 m。

調保計算要求：蝸殼末端最大壓力不超過55 m，機組轉速最大上升率小于50%，尾水管進口最小壓力不低于-8 m。電站運行控制工況如下：

工況一：上游水位為校核洪水位78.90 m，下游水位為校核洪水位60.30 m，3臺機組以最大出力運轉，某一時刻，所有機組同時甩全部負荷。該工況為蝸殼末端壓力的控制工況。

工況二：上游水位為75.00 m，下游水位為全廠機組滿發尾水位51.75 m，3臺機組額定水頭，額定流量，以額定出力運轉，某一時刻，所有機組同時甩全部負荷。該工況為機組轉速上升率的控制工況。

仿真計算模型中包含引水明渠、前池、壓力鋼管、機組、尾水管、尾水池、尾水明渠。本水電站發生甩負荷時導葉的關閉時間較短(10 s以內)，在這個很短的時間內，前池水位升高，尾水池水位降低，但變化幅度均很小(經計算不到0.1 m)。導葉關閉之后，前池和尾水池中的水位呈現出周期性的波動并逐漸衰減，其中前池波動幅度約1.7 m，波動周期約270 s，尾水池波動幅度和周期略小于前池。由于前池和尾水池水位波動幅度遠小于導葉關閉引起的水錘壓力，且水位波動周期遠大于水錘周期，所以前池和尾水池的水位波動對調節保證極值沒有影響。

根據大量試算，水輪機導葉采用8 s一段直線關閉規律較為合適。在此基礎之上，采用不同的槳葉動作規律對工況1和工況2進行過渡過程計算，工況1槳葉初始開度為4.14°，工況2槳葉初始開度為8.67°。

槳葉動作規律1：30 s一段直線關閉，關閉至-14°；

槳葉動作規律2：始終保持開度不變；

槳葉動作規律3：30 s一段直線開啟，開啟至14°。

不同槳葉動作規律的計算結果如表1及圖2～5所示。

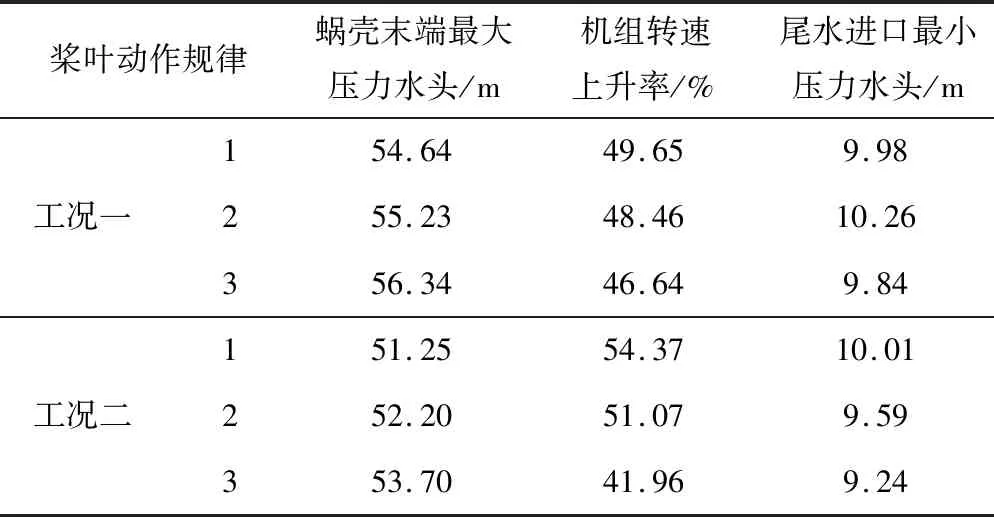
表1 不同槳葉動作情況下計算結果Tab.1 Calculation results under different blades actions

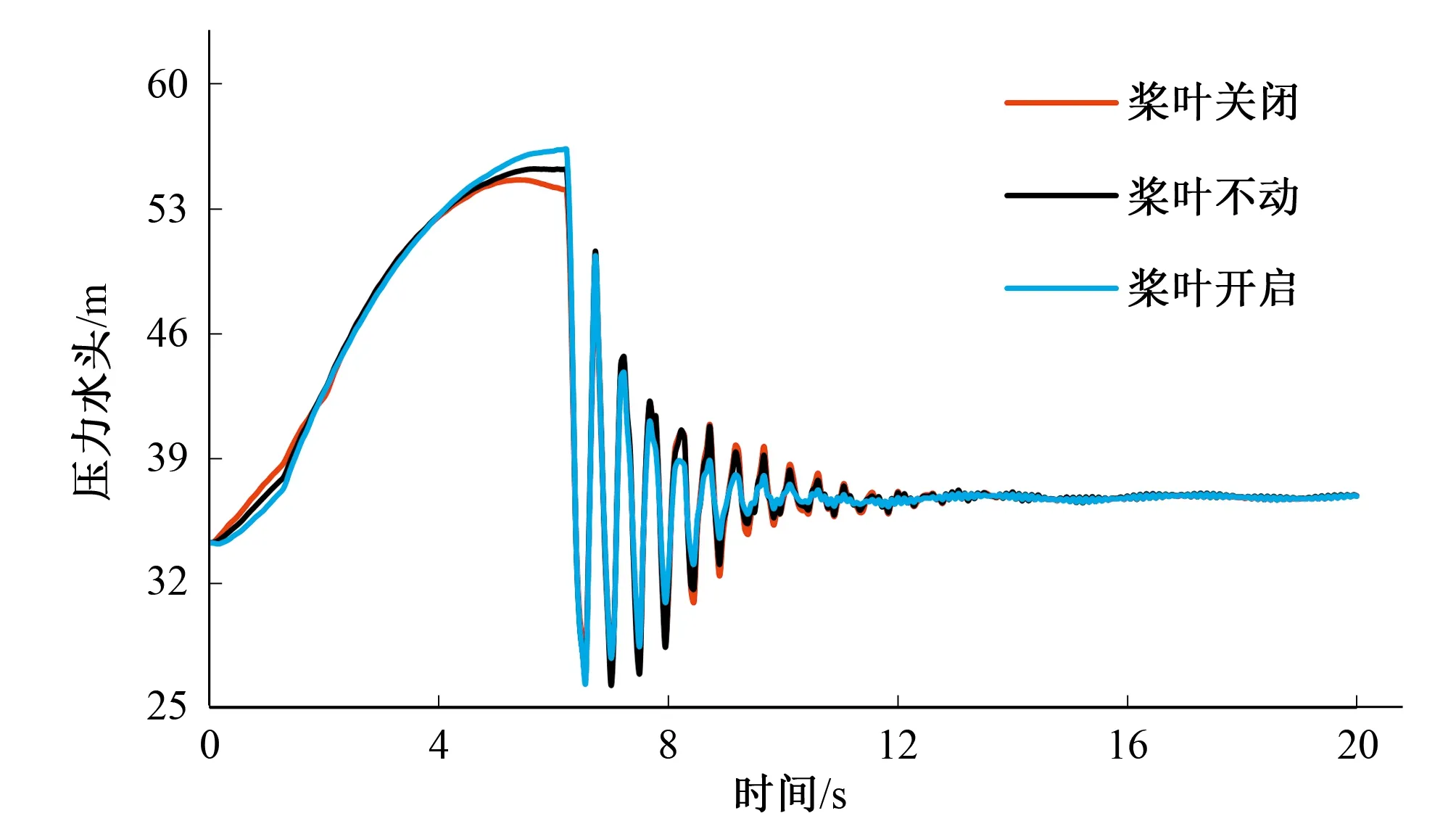
圖2 蝸殼末端壓力隨時間變化圖(工況一)Fig.2 Pressure change with time at the volute end (condition 1)

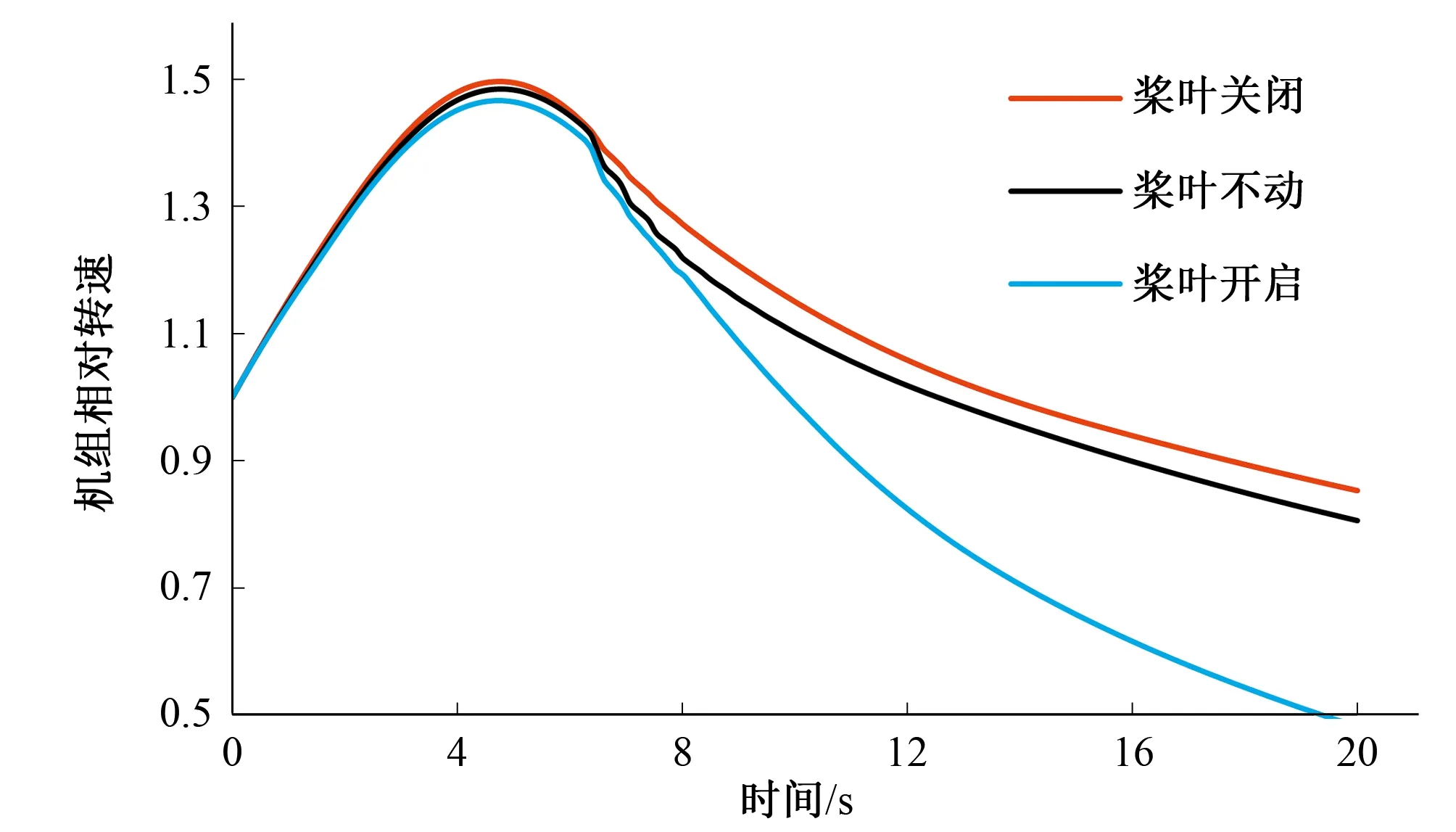
圖3 機組相對轉速隨時間變化圖(工況一)Fig.3 Relative speed change with time of the unit (condition 1)

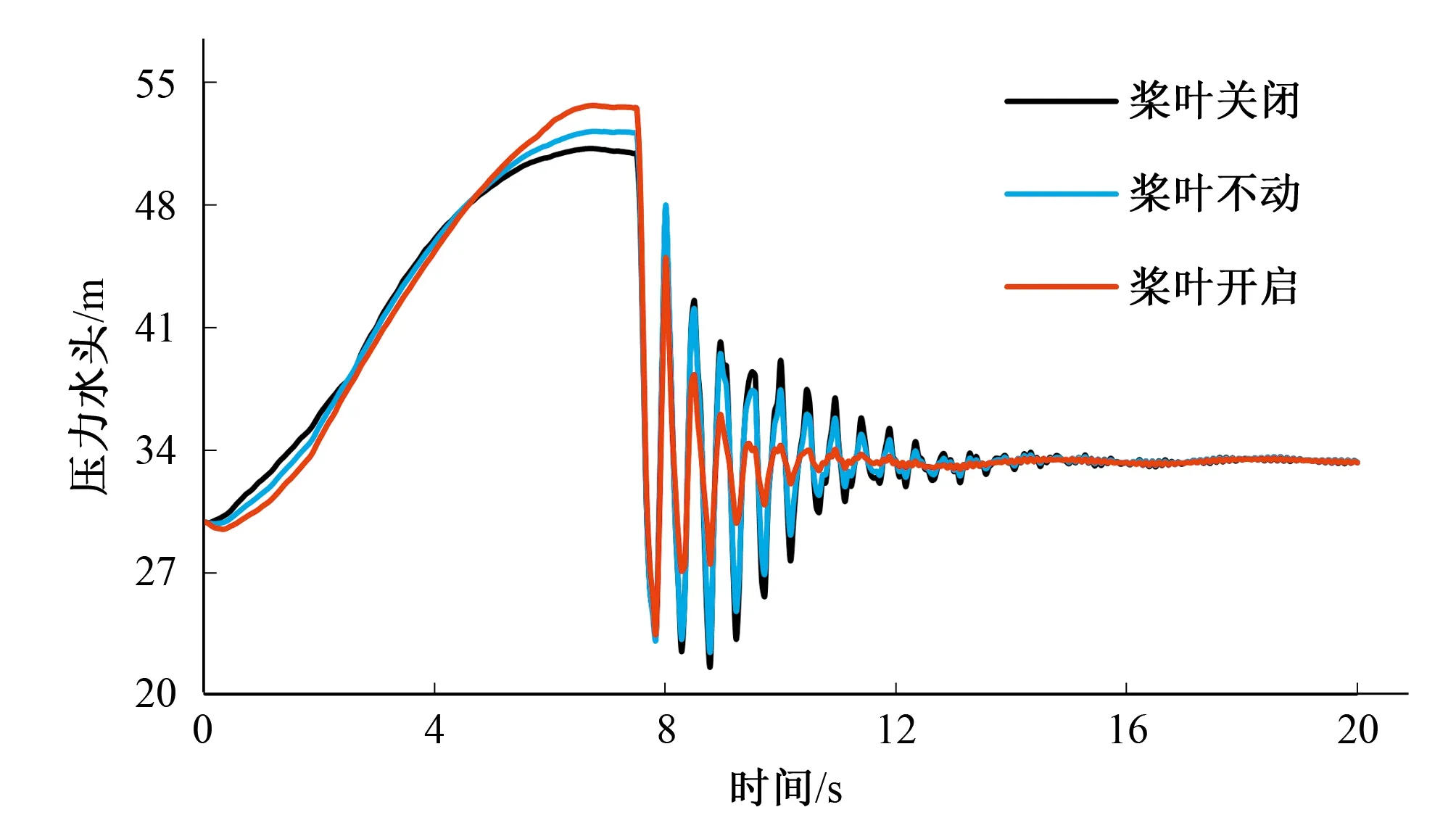
圖4 蝸殼末端壓力隨時間變化圖(工況二)Fig.4 Pressure change with time at the volute end (condition 2)

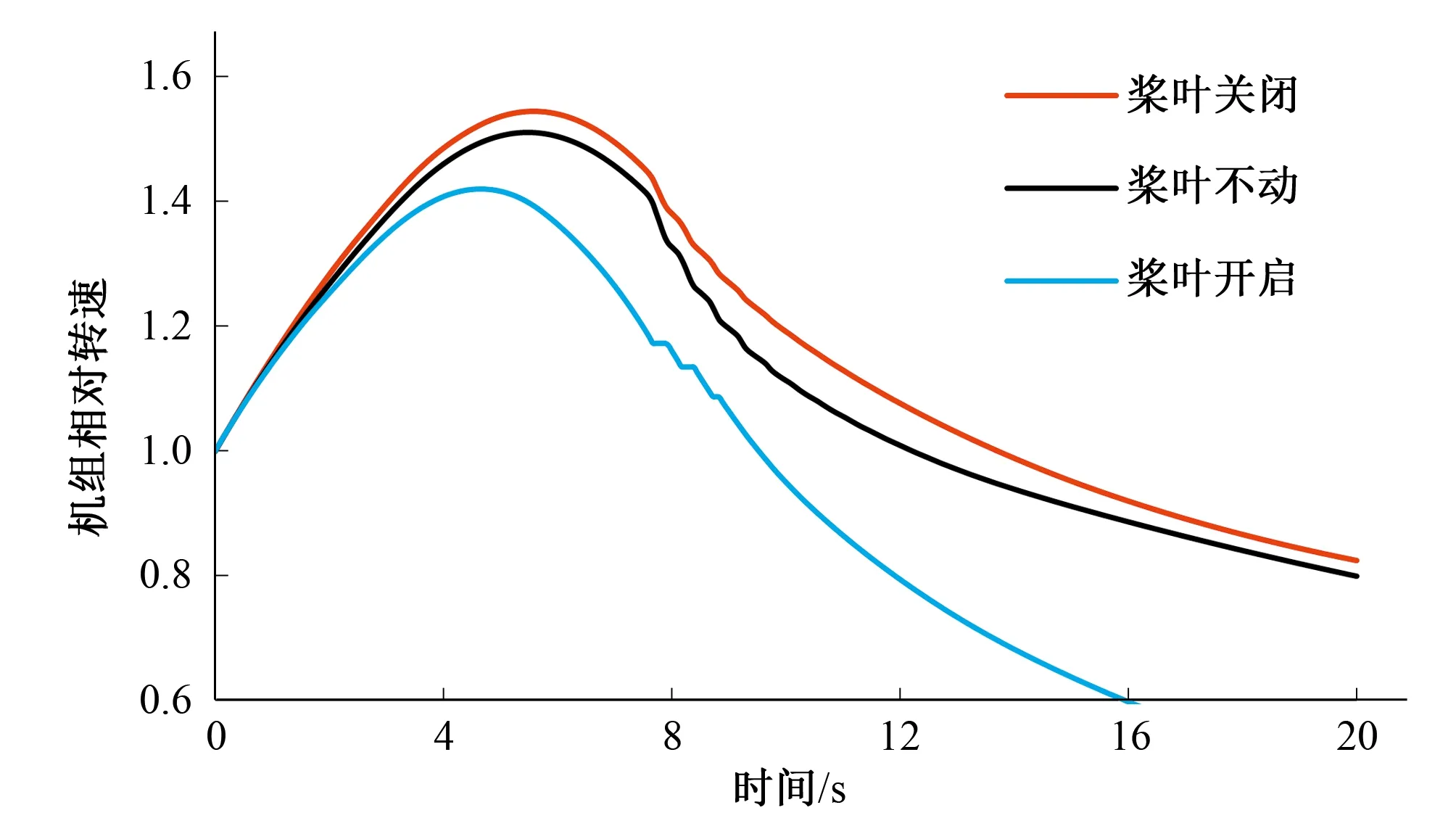
圖5 機組相對轉速隨時間變化圖(工況二)Fig.5 Relative speed change with time of the unit (condition 2)

由表和圖可以看出：當水輪機導葉采用相同的一段直線關閉規律，槳葉依次采用開啟、不動作、關閉的動作方式時，機組最大轉速上升率有了明顯的降低，而蝸殼末端最大壓力有了微小的升高(槳葉30 s開啟與30 s關閉相比，機組最大轉速上升率從54.37%下降到46.64%，下降了14%；蝸殼末端最大壓力從54.30 m上升到了56.20 m，僅僅上升了3.38%)。

機組最大轉速上升率下降的原因是因為在槳葉開度較大情況下，機組的飛逸轉速較小，由此可以推測：甩負荷過渡過程中，槳葉開啟越快，機組轉速上升率的降幅越大。所以采用槳葉開啟的方式，雖然在一定程度上會造成蝸殼末端壓力上升，但其增加值與機組轉速最大上升率的降低值相比小了很多，若將導葉關閉時間縮短，可以達到同時改善兩者的效果。因此該槳葉動作方式總體來說對水電站調保計算是有利的。

下面通過機組流量分析壓力上升原因。圖6為某一固定槳葉開度下的綜合特性曲線圖，圖7～8分別為兩個工況下過渡過程計算中流量變化過程線。

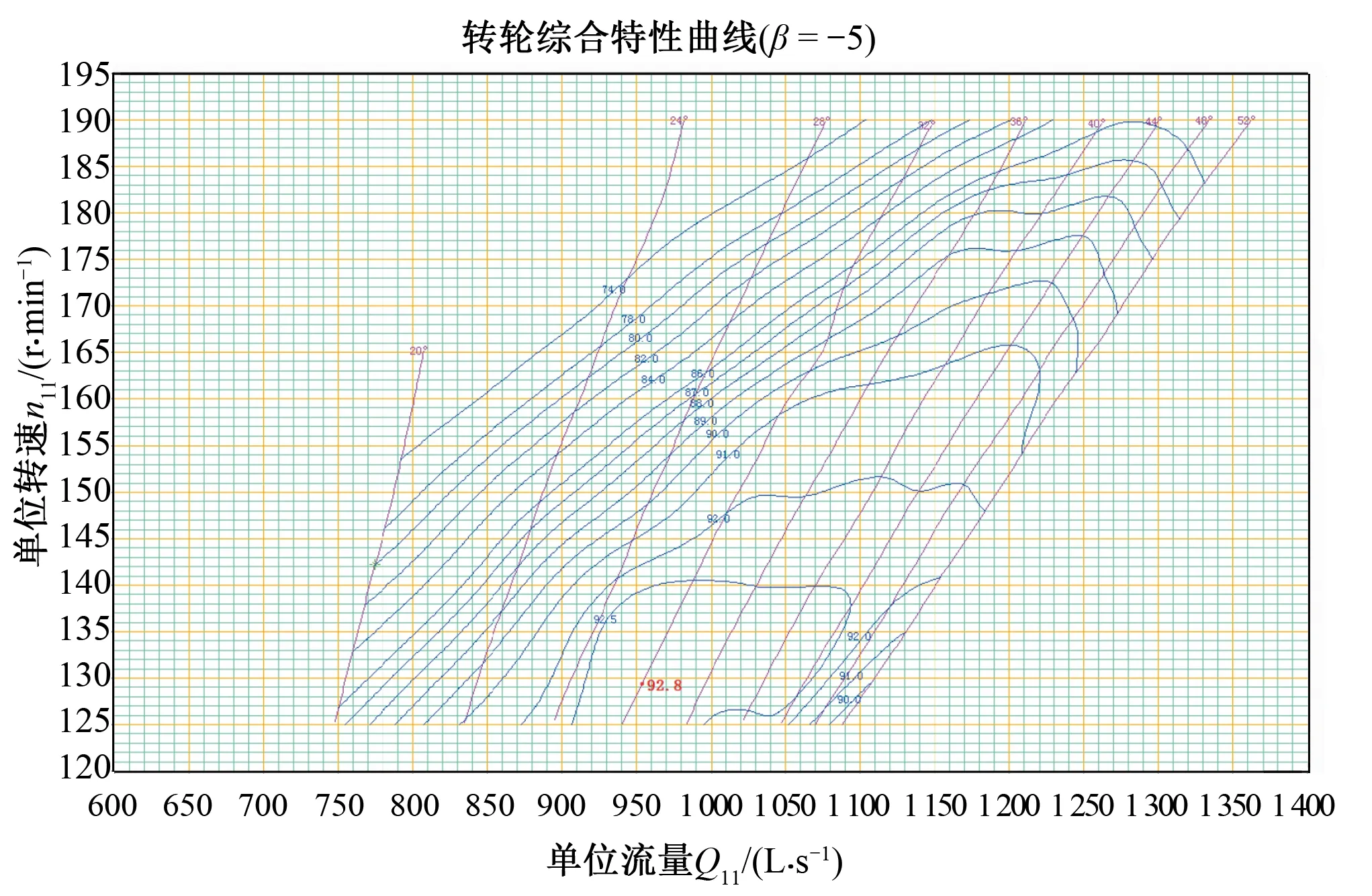
圖6 某一固定槳葉開度下綜合特性曲線Fig.6 Turbine synthetic characteristic curve in a fixed blade opening

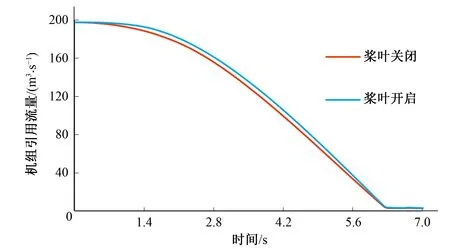
圖7 機組流量變化圖(工況一)Fig.7 Unit flow change with time (condition 1)

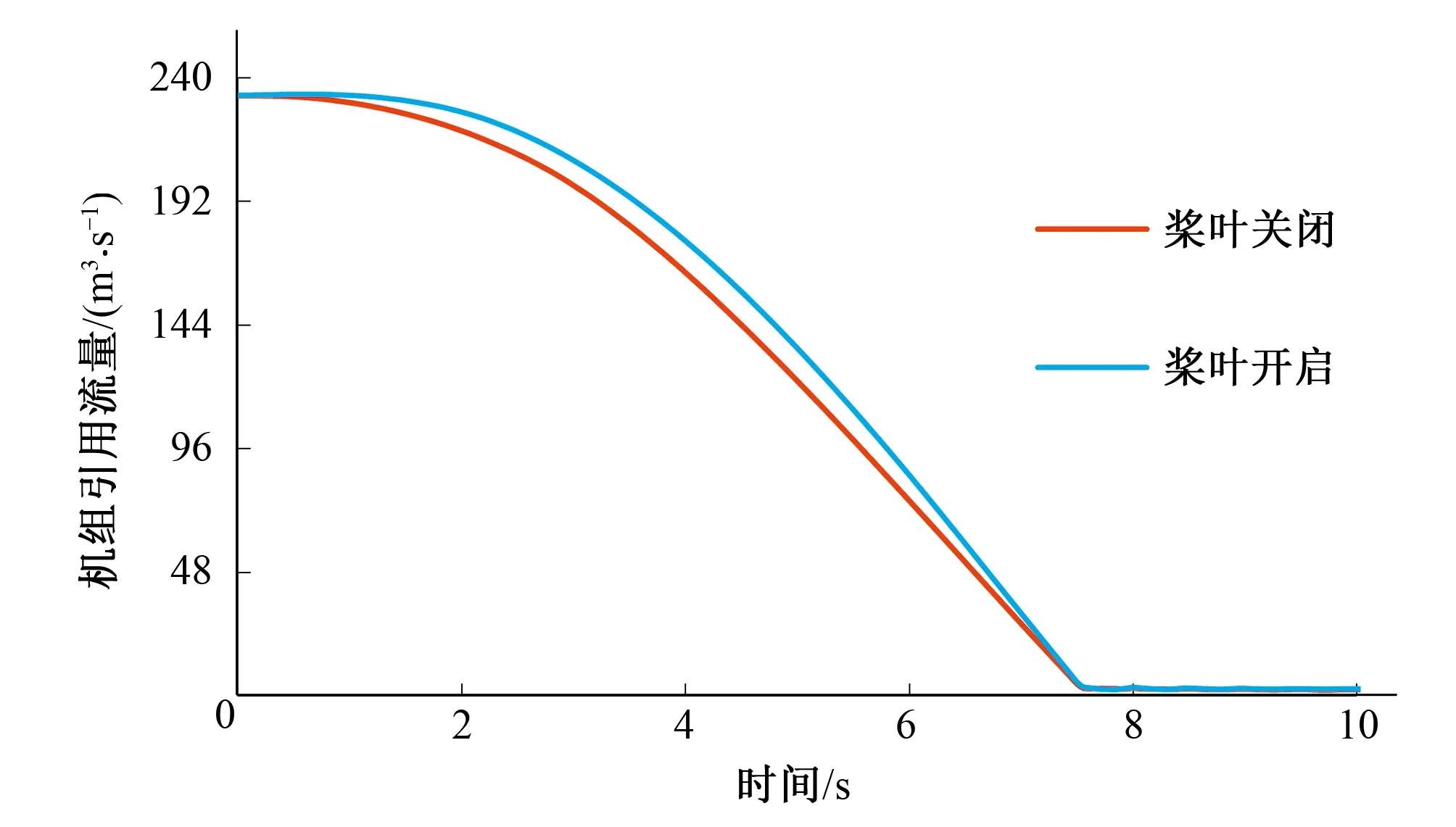
圖8 機組流量變化圖(工況二)Fig.8 Unit flow change with time (condition 2)

從綜合特性曲線圖中可以看出，該水輪機的比轉速較高，對于相同導葉開度，單位轉速越大，單位流量越大，因此理論上適合采用先快后慢的關閉規律。而由兩個工況的流量變化圖可以看出，槳葉開啟與槳葉關閉相比，其流量減小規律略微呈現出先慢后快的特點，這對蝸殼末端最大壓力不利。

綜上所述，在甩負荷過渡過程中，在導葉關閉的同時槳葉快速開啟可以明顯降低機組轉速上升，而蝸殼末端最大壓力略微增加。通過選用合理的導葉關閉與槳葉開啟規律，可以有效地平衡蝸殼末端最大壓力和機組最大轉速上升率，使兩者均有較大的安全裕量。

2 導葉關閉規律優化

機組導葉采用兩段折線關閉規律通常能夠同時降低甩負荷過程中的蝸殼末端最大壓力和機組最大轉速，但兩段折線關閉規律涉及的變量多，變量取值范圍廣。常規的優化方法是隨機選擇幾組不同的關閉規律進行仿真計算，然后選擇計算結果較好的那組關閉規律作為實際工程使用，這種方式無疑具有很大盲目性，選擇結果的優良主要依賴于設計人員的經驗。為了解決這一問題，本節采用一種非線性的導葉關閉規律的優化模型，通過一種智能優化方法----模擬退火優化算法，對上一節中初步計算得到的導葉-槳葉協聯動作規律進行優化計算，得出符合調保計算的較優動作規律。

2.1 優化模型

評價函數：

(1)

式中：Hv，con、Nt，con、Ht，con分別是機組蝸殼最大內水壓力、機組轉速最大上升率、尾水管最小內水壓力的控制值；Hmax、Nmax、Hmin分別是蝸殼最大內水壓力、機組轉速最大上升率、尾水管最小內水壓力的計算值；a，b，c分別3個調保參數的權重系數；k為評價值放大系數；E為關閉規律的評價值。

由于蝸殼末端最大壓力和機組轉速最大上升率可能發生在不同的工況中，所以優化計算應該采用可以進行多工況計算的優化模型：

Hmax=(Hmax,1,Hmax,2,…,Hmax,n)

Nmax=(Nmax,1,Nmax,2,…,Nmax,n)

Hmin=(Hmin,1,Hmin,2,…,Hmin,n)

(2)

式中：n是參與優化計算的工況個數；Hmax，i，Nmax，i，Hmin，i分別是各個工況下計算出來調節保證計算指標值(i的取值范圍為1～n)；Hmax，Nmax，Hmin分別是所有工況中相應調節保證計算指標的最大值[12]。

2.2 模擬退火算法

模擬退火算法是一種新型的多目標優化計算方法，在諸多領域均有廣泛的應用，其中水利領域中的水資源優化配置[13]、梯級水電站調度[14]等復雜問題的優化計算有較好應用效果。由于篇幅限制，算法的具體優化原理和計算步驟可見參考文獻[12]，這里不再詳述。

2.3 優化計算

下面基于水輪機導葉關閉規律優化模型和模擬退火算法，對兩段直線導葉關閉規律進行優化(槳葉均采用30 s一段直線開啟的動作規律)。

優化算法的參數設定為：初始溫度設置為1 000 ℃，每個溫度值下優化3次，結束溫度設置為5 ℃。即初始狀態溫度設定為1 000 ℃，在該溫度下隨機給定一個兩段折線關閉規律，進行過渡過程計算，并采用評價函數計算評價值，作為初始條件。接著在當前關閉規律的基礎之上，在一定范圍內隨機產生一個新的兩段折線關閉規律，并進行過渡過程計算，根據計算結果計算評價值，若新評價值比原評價值好，則接受新的兩段折線關閉規律為當前溫度下的最優解，否則按照一定概率拒絕接受新的兩段則先關閉規律(此概率與狀態溫度有關，溫度越高，此概率越大)。在該溫度下進行3次優化計算，然后根據預先設置好的冷卻進度表降低狀態溫度。在新狀態溫度下進行3次以上優化過程，然后繼續降低狀態溫度，最終停止優化的條件是狀態溫度降低至5 ℃。

根據2.2節的計算可知，由于該電站尾水管比較短，尾水管進口最小壓力在導葉采用直線關閉規律時已經滿足調節保證計算要求，所以優化函數中可以剔除尾水管進口最小壓力這一項。而此電站中的蝸殼末端最大壓力和機組最大轉速上升率均是比較重要的控制指標，所以兩者的權重系數給相同大小。

為了保證優化計算結果的可靠，分別采用3個不同的初始關閉規律U01=(7，8，0.4)、U02=(9，8，0.4)、U03=(8，8，0.7)進行多次計算，優化結果如圖9所示。

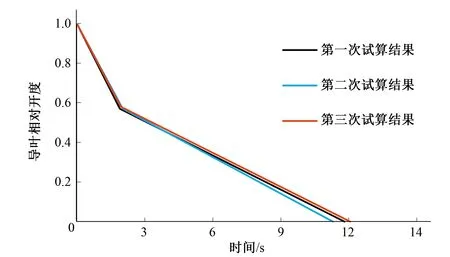
圖9 3次優化計算得到的關閉規律示意圖Fig.9 Three closing laws obtained by optimization calculation

根據示意圖可知3個不同初始關閉規律優化計算得到的結果基本一致：Ub1=(4.40，17.41，0.57)、Ub2=(4.71，16.28，0.57)、Ub3=(4.60，17.47，0.58)，說明優化計算是可靠和穩定的。對比3個優化計算結果，無論初始關閉規律給定的是一段直線關閉還是分段直線關閉，無論給定的初始折點開度是多少，通過模擬退火算法計算，都可以優化得到相近似的結果，這說明優化計算的過程是穩定的。將Ub1、Ub2、Ub33種折線關閉規律分別帶入工況一和工況二中進行數值仿真計算，計算得到的結果如表2所示：

表2 不同關閉規律情況下的計算結果Tab.2 Calculation results under different closing laws

對比表2和表1可以看出，使用模擬退火算法優化得到的導葉-槳葉協聯關閉規律，兩個控制工況下的蝸殼末端最大壓力與機組轉速最大上升率均有明顯下降，且安全裕量分配較為合理。從圖10中可以看出，導葉快關造成的第一波水錘壓力最大值和導葉慢關造成的第二波水錘壓力最大值基本接近，進一步說明優化得到的關閉規律是合理的，能夠將整個導葉關閉期間的蝸殼水錘壓力控制的較為平均。

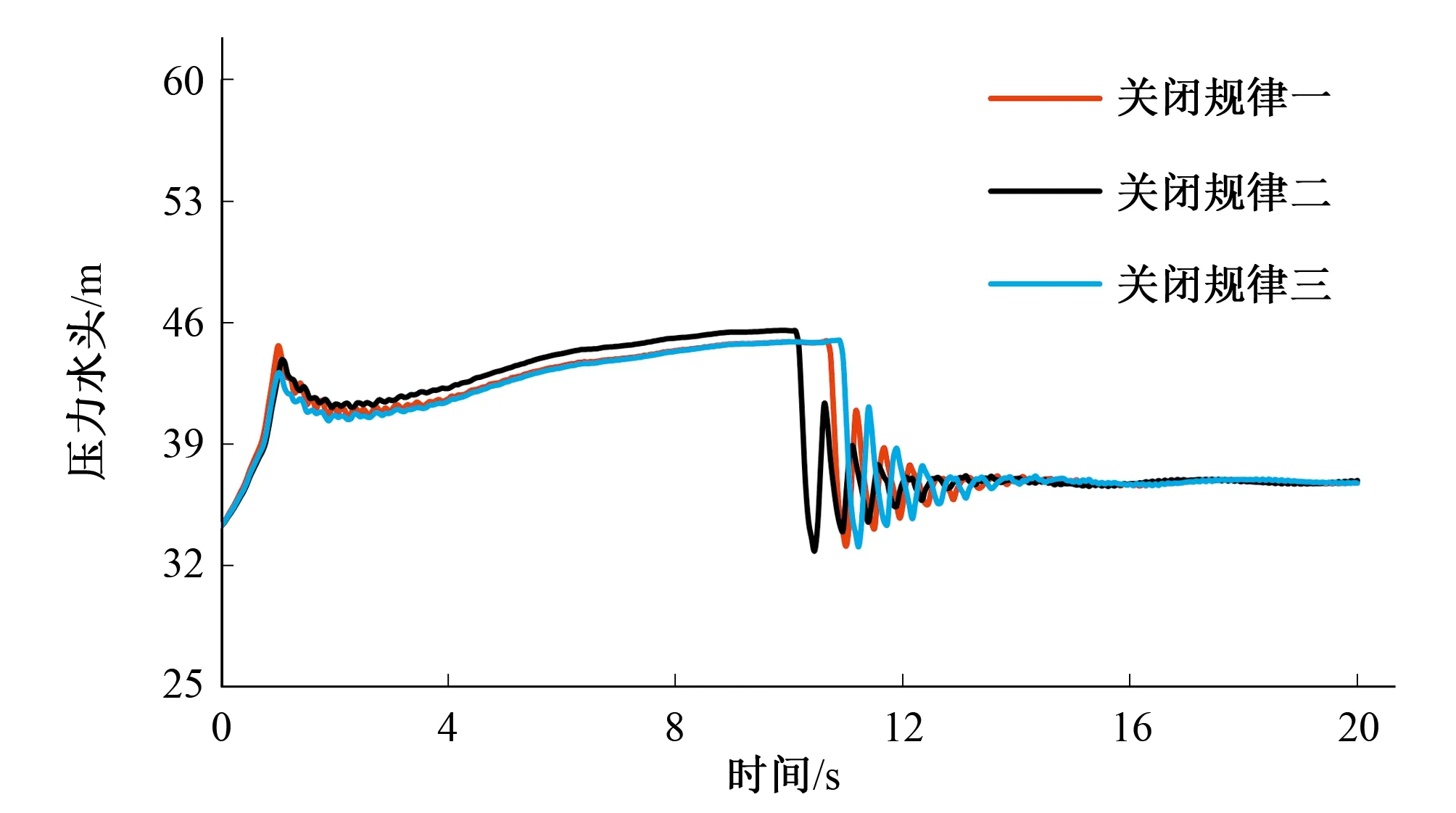
圖10 蝸殼進口壓力隨時間變化圖(工況一)Fig.10 Pressure change with time at the volute end (condition 1)

根據以上優化計算過程可以得到適合該軸流轉槳式機組的甩負荷協聯關閉規律，采用這種關閉規律，調保計算指標能夠滿足設計要求。

3 結 語

本文通過分析軸流轉槳式水輪機飛逸曲線的特點，提出一種適合轉槳式機組的協聯關閉規律，并結合工程實例，采用數值模擬手段，證明了該關閉規律的可行性。最后，采用多工況非線性優化模型和模擬退火智能算法對提出的協聯關閉規律進行優化，得到調節保證計算參數安全裕量分配較為合理協聯關閉規律。結果表明：

(1)轉槳式機組發生甩負荷時，槳葉開啟、導葉關閉的協聯動作方式可以大大降低機組轉速最大上升率，而蝸殼末端壓力會有略微上升，但上升幅度很小。

(2)通過非線性優化模型，采用模擬退火算法可以對新型協聯關閉規律進行優化計算，優化結果能夠很好地滿足調節保證計算的控制要求，且安全裕量分配較為合理。

此外，本文提出此種關閉規律僅考慮了蝸殼末端最大壓力、機組轉速最大上升率以及尾水管進口最小壓力三項調保計算指標，實際上，轉槳式機組的軸向水推力問題也很重要，關于該關閉規律會對機組軸向水推力產生何種影響將會進一步研究。

□