溫度影響下基于協整的頻率修正研究

黃 然

(合肥工業大學 土木與水利工程學院，安徽 合肥 230009)

0 引 言

近年來,橋梁健康檢測技術愈發成熟和完善,基于動力的結構健康監測是目前研究最為廣泛的一個方向,橋梁結構的動力參數是橋梁健康監測的一個重要指標,結構動力參數識別是基于結構動態測試的模態分析方法,模態參數(通常是模態頻率)反映了結構的健康狀態信息。通過研究橋梁模態參數的改變來對橋梁健康狀態進行監測和量化評估,是進行橋梁健康監測的基本思路[2]。

先前的研究表明溫度是影響模態參數尤其是模態頻率的最主要因素,主要原因有:① 溫度可以直接影響材料的彈性模量,而通常f～E1/2;② 溫度變化可以影響結構的邊界條件,例如冬季基礎凍結會提高結構的整體剛度;③ 溫度的變化在超靜定結構會產生溫度應力,應力的改變進而會引起頻率的改變。例如,Alampalli[3]通過對一小橋研究表明,由于溫度下降邊界支座凍結導致的橋梁固有頻率的變化(變化幅度為=40%～50%)比人為造成損壞而導致頻率變化(變化幅度為=3%～8%)大了一個數量級。Askegaard等[4]發現,一座3跨人行橋的正常頻率在一年中變化10%。

因此,在實際橋梁結構健康監測中環境因素的影響不可忽視,如何從健康監測系統中分離出溫度因素的影響一直是健康監測領域研究的熱點和難點。因此,本文引入計量學中的協整理論,它在健康監測系統中分離這些無害的環境變化被證明具有巨大的潛力。

1 協整理論

1.1 概述

Cross[5]最先提出將計量學中的協整理論應用到結構健康監測領域,并且詳細分析協整為何可被應用到結構健康監測中。這里首先介紹單整的定義,如果一個序列經過一次差分后變成平穩的,就稱該序列是一階單整序列,記為I(1)。一般地,如果一個時間序列經過d次差分后變成平穩序列,則稱原序列是d階單整序列,記為I(d)。

而協整的定義最早是由Engle和Granger[6]給出的:

由n組的d階單整序列組成的向量yt=[y1t,y2t,…,ynt]′,如果存在一個向量β=[β1,β2,…,βn]′使得線性組合βyt=β1y1t+β2y2t,…,+βnynt是一個d-b階單整,其中b>0。則向量yt=[y1t,y2t,…,ynt]′稱為d、b階協整,記為yt～CI(d,b),向量β稱為協整向量。

1.2 ADF檢驗

協整是分析非平穩序列的一種工具,在應用協整之前需要對序列進行平穩性判斷,確定序列的單整階數,這里采用ADF檢驗。ADF檢驗是在Dickey和Fuller[7,8]提出的DF檢驗基礎上擴展形成的。對于一個p階自回歸模型AR(p):

yt=α1yt-1+α2yt-2+…+αpyt-p+ut

(1)

對式(1)進行差分和整理得:

Δyt=δyt-1+η1Δyt-1+…+ηp-1Δyt-p+1+ut

(2)

式中:δ=α1+α2+…+αp-1;ηi=-(αi+1+…+αp);ut是白噪聲。

當δ=0時,即α1+α2+…+αp=1,此時式(2)作為一個線性差分方程,其對應的特征方程λp-α1λp-1-α2λp-2-…-αp=0必存在一個單位根,因為λ=1是該特征方程的一個解,1-α1-α2-…-αp=0。ADF檢驗的原假設和備用假設是H0∶δ=0和H1∶δ<0。

確定了各個變量的單整階數后,在滿足協整前提下就可以使用Johansen程序對多個序列之間是否存在協整向量進行檢驗。

1.3 Johansen協整檢驗

Johansen[8,9]給出了一種基于矩陣的秩和特征根的協整檢驗方法,稱為Johansen協整檢驗。考慮不包含截距項的n維p階VAR模型:

Yt=A1Yt-1+A2Yt-2+…+ApYt-p+et

(4)

對上式(4)進行變形整理可以得到:

(5)

在滿足r(π)=r的條件下,最大化樣本數據[y1t,y2t,…,ynt]′的對數似然函數。為此,須先確定協整秩r。當協整秩為r時,系數矩陣π有r個自由(線性無關)的行向量。當協整秩r越大,對矩陣π的約束越少,對應的似然函數最大值應該越大。

據此進行似然比檢驗,由于檢驗統計量涉及矩陣的跡(主對角線元素之和),故稱為“跡統計量”(trace statistics),記為λtrace。

“跡檢驗”(trace test)是似然比檢驗,為單邊右側檢驗,為單邊右側檢驗,即λtrace越大,則越傾向于拒絕原假設。

故首先進行以下檢驗:

H0∶r(π)=0vsH1∶r(π)>0

原假設為協整秩為0,不存在協整關系;替代假設為協整秩大于0,存在協整關系。如果接受原假設H0∶r(π)=0,則認為不存在協整關系。反之,繼續檢驗是否存在多個協整關系,其對應的原假設和備選假設為:

H0∶r(π)=1vsH1∶r(π)>1

如果依舊拒絕原假設,則依次順序不斷進行以下檢驗：

H0:r(π)=2vsH1:r(π)>2

?

H0:r(π)=rvsH1:r(π)>r

直到接受原假設,確認協整秩r為止,即序列之間存在r個協整向量。

2 試驗模型監測數據的采集和處理

2.1 試驗模型

為了深入研究協整算法在消除環境溫度的影響,本文以一個長3 m兩端固結的鋼梁為研究對象,梁兩端各使用4個高強螺栓固定在支座上,每個支座通過2個地錨固定在預留在地面的槽中。試驗將整個梁劃分15等份,共布置14個加速度傳感器用以采集梁體的振動信號,加速度采樣頻率為500 Hz。除此之外,還在梁上布置3個溫度傳感器用以記錄試驗過程中梁體的溫度變化,加速度的布置和激振器布置如圖1所示。

圖1 加速度傳感器和溫度傳感器布置

2.2 試驗數據的采集和數據處理

為了得到梁的頻率隨溫度變化的關系,分別對梁進行升溫和降溫兩種操作,在溫度變化的過程中對梁使用激振器進行脈沖激勵,溫度變化過程中使用高精度的加速度傳感器采集梁體的振動信號、使用溫度傳感器采集梁體的溫度變化。對采集的加速度數據進行模態參數識別。

梁在無損狀態下前4階頻率的時間序列的曲線圖如圖2所示。

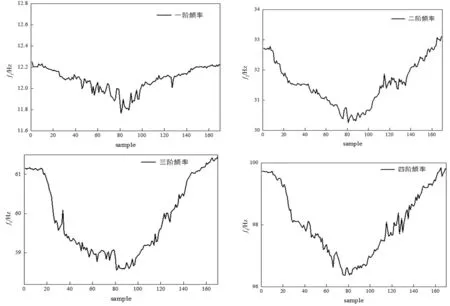
圖2 前4階模態頻率識別值變化曲線圖

從圖2中可以看出,一方面結構的前4階頻率的變化趨勢和溫度變化呈相反的趨勢,隨著溫度的升高結構的頻率逐漸降低,另一方面各階頻率隨著溫度變化都呈現出相同的趨勢。

2.3 基于協整消除溫度對結構頻率的影響

在進行Johansen協整檢驗之前,第一步需求被檢驗變量是同階單整的,分別對這4個頻率序列進行ADF單位根檢驗,檢驗的結果見表1。

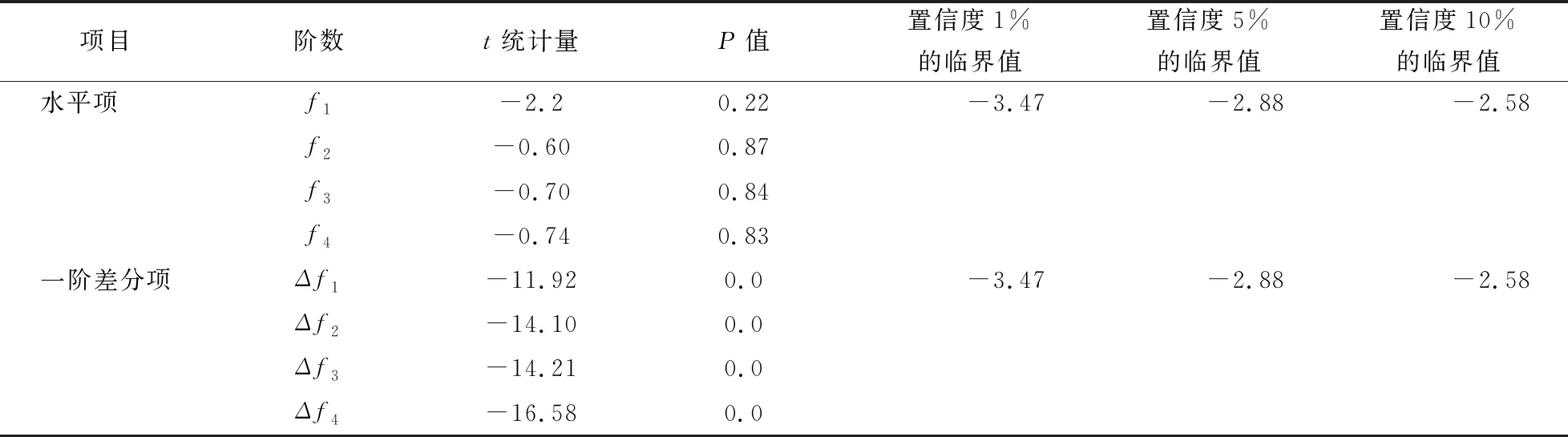
表1 結構前4階頻率以及差分項ADF單位根檢驗結果

由表1可以看出,結構的前4階頻率均不能拒絕單位根的原假設,其一階差分項在5%的顯著性水平下均拒絕原假設,表明這4個頻率序列均為一階單整,即滿足Johansen協整的前提條件。圖3描繪了各階頻率之間的關系,從圖3中可以看出,f1,f2和f4之間有比較明顯的線性關系,而f3與其他各階頻率之間沒有明顯的線性關系[10],這也進一步顯示了各階頻率序列之間可能會存在某種線性組合。在確定Johansen協整檢驗的方程特征時,協整方程存在截距項,沒有趨勢項,這4個變量的檢驗的結果見表2。

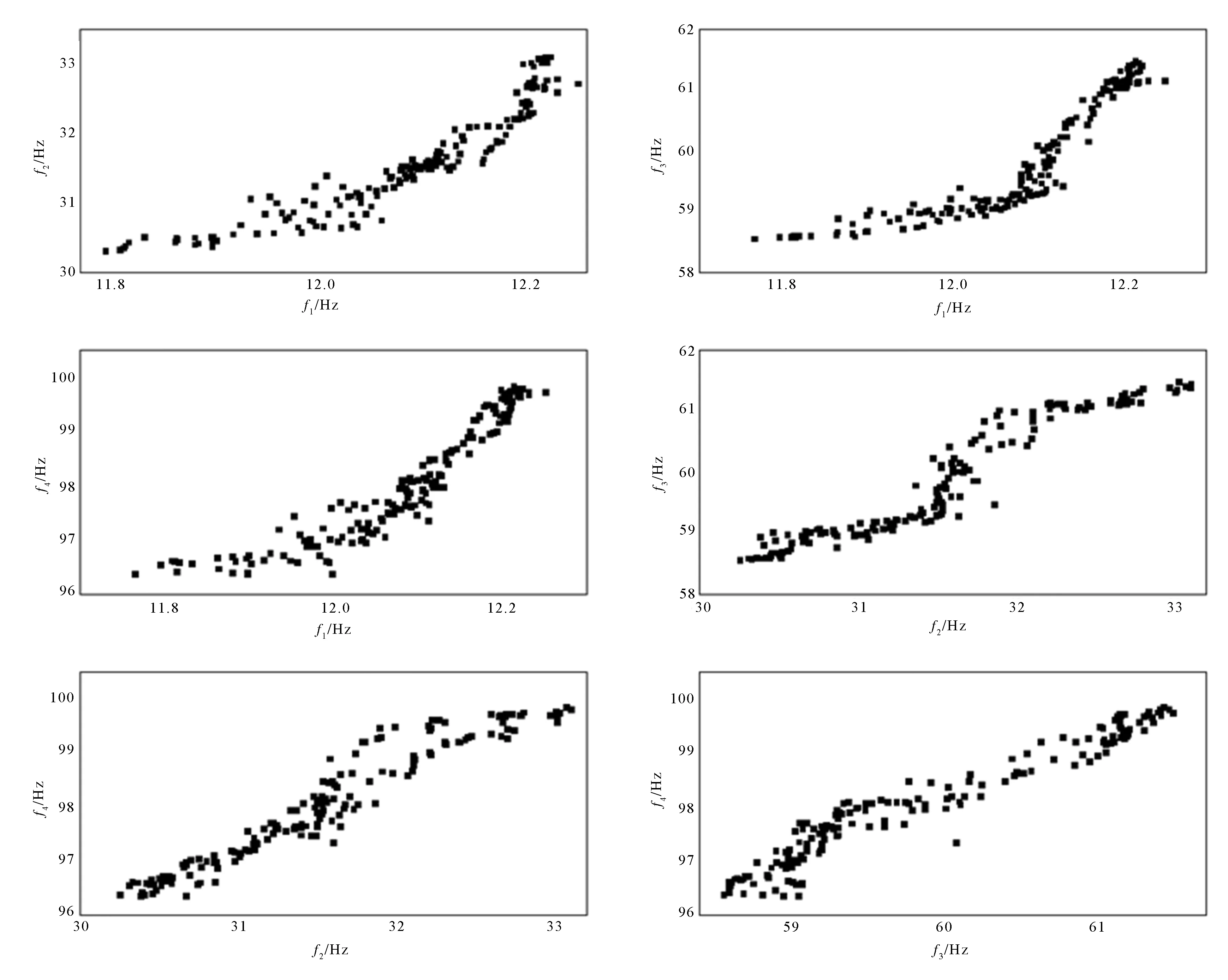
圖3 各階頻率之間關系散點圖

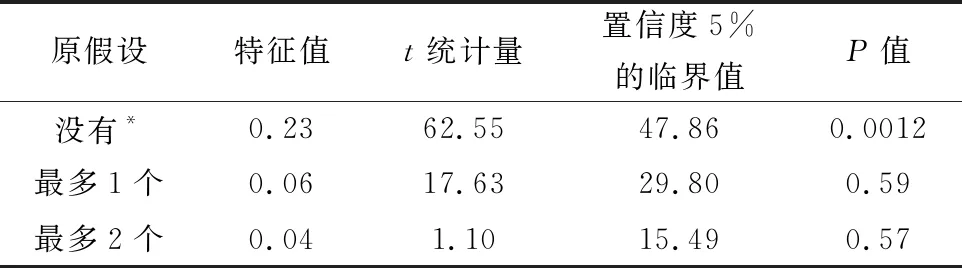
表2 Jonhansen檢驗結果

由檢驗結果可知,4階頻率之間存在且只存在唯一的協整關系,通過計算可以得到標準化的協整向量為[1,-0.1813,-0.1713, 0.3670,-7.9295],因此,各個頻率序列之間的協整方程可以表示為:

f1+0.1813f2+0.1713f3-0.3670f4+7.9295=0

將結構的前4階頻率利用上面的協整方程計算出協整余量序列，如圖4所示。圖4中上下兩條控制線為協整余量的均值±3標準差,根據協整理論可知,如果兩個或多個變量是協整的,那么它們的線性組合是原始數據集中共同趨勢的一個固定殘差。就結構健康監測所測的參數而言,它所消除的共同趨勢就是環境和運營條件的改變,在本例中消除的就是溫度因素。

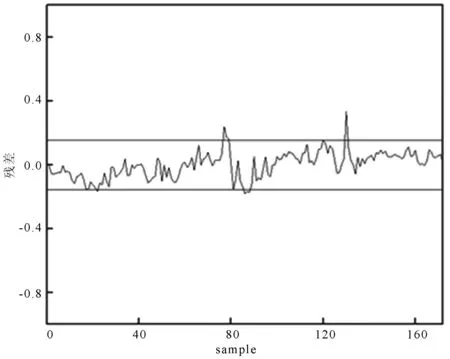
圖4 協整余量曲線

3 結 論

(1) 結構在無損狀態下,隨著環境溫度的升高,結構的頻率逐漸降低,且多階頻率在溫度的變化下都呈現共同的趨勢。

(2) 通過協整分析可知,結構的前4階頻率之間存在協整關系,通過線性組合得到一個消除多個變量共同趨勢的平穩殘差，并且殘差序列在一定的范圍內波動，可以通過序列是否偏離控制線來判斷結構的狀態。

(3) 與其他消除環境因素的方法相比,協整具有以下優勢:① 原理簡單,理論明確;②不需要對原始序列進行處理,保留了序列的原始特性。