基于廣義S變換的時變索力識別
曹志偉
(合肥工業大學 土木水利工程學院,安徽 合肥 230009)
0 引 言
索體系支承橋梁中纜索或者吊桿是其關鍵的傳力或承力構件。如斜拉橋通過斜拉索將主要荷載傳遞至主塔。所以對于斜拉橋這種索體系支承橋梁來說,索力的準確識別和評估對于大跨度的斜拉橋的運營狀況的評定和健康的維護都有著至關重要的意義[1]。目前,針對施工和運營等不同階段及不同環境有不同的索力識別方法。常用的索力識別方法按識別過程通常可分為:直接法(包括壓力傳感器法和壓力表法)和間接法(包括磁通量法和頻率法[2])。
其中頻率法具有簡易便捷、無損性監測等優點,越來越受到人們的關注。頻率法通過獲取并分析索的振動加速度信號從而得到索的固有頻率,通過數值計算和經驗擬合等方法構建索力和固有頻率之間的換算關系,從而通過對索的固有頻率的識別實現對索力的識別。因此基于頻率法的索力識別需要解決兩個核心問題,第一個是建立拉索索力與其固有頻率之間的對應關系;第二個問題是如何通過振動信號,準確地對索的固有頻率進行識別。
Irvine等[3]在1974年通過對索振動的動力特性進行研究,首次通過將索的長度、抗彎剛度和索力大小進行綜合分析,并引入參數ξ反映這三個因素的影響。1980年,日本Shinke等[4]考慮了索的抗彎剛度影響,以兩端固結邊界條件的軸向受拉索為模型進行研究,通過建立邊界條件為兩端固結的索的橫向振動微分方程并進行求解,推導出了拉索所受拉力與索固有頻率的隱式解,并通過數值計算和曲線擬合,推導出了兩端固結邊界條件下的索力計算實用公式。1998年,ShiMada等[5]提出了一種用于結構索振動分析的有限差分公式。該公式將索的彎曲剛度及其垂伸特性的影響統一求解,為準確確定振型和頻率提供了工具。2007年,韓國學者Kim等[6]提出了一種從測量索的固有頻率來估計索的張力的新方法。該方法能夠同時識別拉索系統的張力、抗彎剛度和軸向剛度。該方法適用于廣泛的纜索系統。
雖然近年來國內外對于索力識別的頻率法研究進了許多工作,針對索的抗彎剛度、索長度、外界溫度、邊界條件等因素做了大量研究。但是傳統基于頻率法的索力識別方法只能識別索在過去一段時間內的平均索力,無法對索力進行實時的識別。在實際的環境中,索力往往是隨時間而變化的,因此如何實時識別固有頻率轉化為從索的動態響應中提取瞬時頻率。針對這個問題,本文將廣義S變換方法應用于時變索力的識別,從而能夠對索力進行實時識別。
1 頻率法索力計算
Fang等[7]在索的橫向振動方程的基礎上,用曲線擬合技術代替數值迭代過程,提出了一個頻率法計算索力的實用公式。該公式考慮了索的抗彎剛度,是梁理論和弦理論兩種假設下的統一表達式。在無垂度影響的索的橫向振動方程的基礎上,頻率方程可由等式(1)等到。
2(αl)(βl)[1-cos(αl)cosh(βl)]
+[(βl)2-(αl)2]sin(αl)sinh(βl)=0
(1)
式(1)中的α,β由分別由式(2)和式(3)計算。
(2)
(3)
式中:ζ2=T/EI,η4=mω2/EI;ω表示振動系統的角頻率;l為索兩端之間的直線長度。式(1)為一個不便求解的超越方程,索力無法直接簡便地從所測得的頻率求得。引入參數αl=γ,βl=χ。式(1)可表示為:
(4)
χn和γn有如下關系:
(5)
(6)
其中ωn(ωn=2πfn)和fn分別表示振動系統的第n階角頻率和固有頻率。拉力換算公式可表示為:
(7)
在上式中,l,m和EI均為索的已知參數,因此只要確定索的第n階振動頻率,就能通過式(5)和式(6)解得χn和γn,從而根據式(7)獲取索所受拉力。為使式(7)能夠適應不同假設下進行索力計算,引入參數ψn,其定義為:
(8)
在γn和ψn之間得到一個二次最優擬合函數,其方程為:
(9)
上式中,A和B通過式(10)和式(11)計算。
A=-18.9+26.2n+15.1n2
(10)
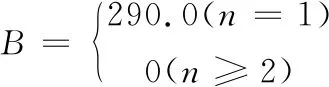
(11)
可以看出,當n=1時采用二次擬合,n≠1時采用線性擬合,以減小誤差。
2 廣義S變換基本原理
S變換[8]是由小波變換和短時傅里葉變換發展而來的,與STFT類似,S變換是在傅里葉變換基礎上添加窗函數。可以將標準S變換視為窗函數為高斯函數,且方差為σ=1/|f|時短時傅里葉變換的特殊情況。
對于給定的信號x(t),S變換表達式為:
(12)
上式中,τ是調整時間軸上高斯窗口位置的參數,f是頻率。S變換中高斯窗h(t,f)定義為
(13)
窗函數h(t,f)滿足歸一化條件:
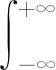
(14)
由式(12)可得:
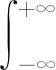
(15)
式中:X(f)為信號x(t)的傅里葉變換,即S變換的逆變換,由傅里葉變換推導得出,其逆變換具有無損性。為使S變換的時頻分辨率能更好地適應不同信號特征,本文通過引入一階雙參數頻率函數[9],以此更靈活對窗函數進行調整。廣義S變換窗函數為:
(16)
式中:參數α和γ為調整窗函數的兩個參數。通過參數α和γ共同調解窗函數的高度和寬度。該窗函數依然滿足歸一化條件,即:
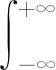
(17)
廣義S變換定義為:
(18)
與S變換類似,廣義S變換的逆變換同樣具有無損性。廣義S變換的逆變換計算公式為:
(19)
由式(16)可以看出,廣義S變換窗函數主要由參數α和p進行人為調節。通過調節參數α和p,能夠較好地調整S變換時窗寬度隨頻率變化的速度,提升S變換的頻率適應性,從而獲得更好的時頻分析效果。
3 實驗分析
為驗證廣義S變換傳遞比對拉索時變索力的識別有效性,本章采用ABAQUS仿真軟件以具體的索結構為對象,構建了一個拉力隨時間變化的索結構的三維有限元模型進行驗證。施加在拉索上的力Ft隨時間t變化,結構的剛度也因此而改變,從而使結構具有時變特性。索結構長度為2 m,橫截面為半徑0.66×10-2m的圓形,泊松比取0.3,楊氏模量為1.95×1011N/m2。
運用廣義S變換預處理后的信號進行計算,對一階頻率進行脊線提取[10]以對結構的瞬時頻率進行識別。
通過瞬時頻率換算得到的拉力曲線與實際加載曲線對比和識別百分比誤差分別如圖1和圖2所示。
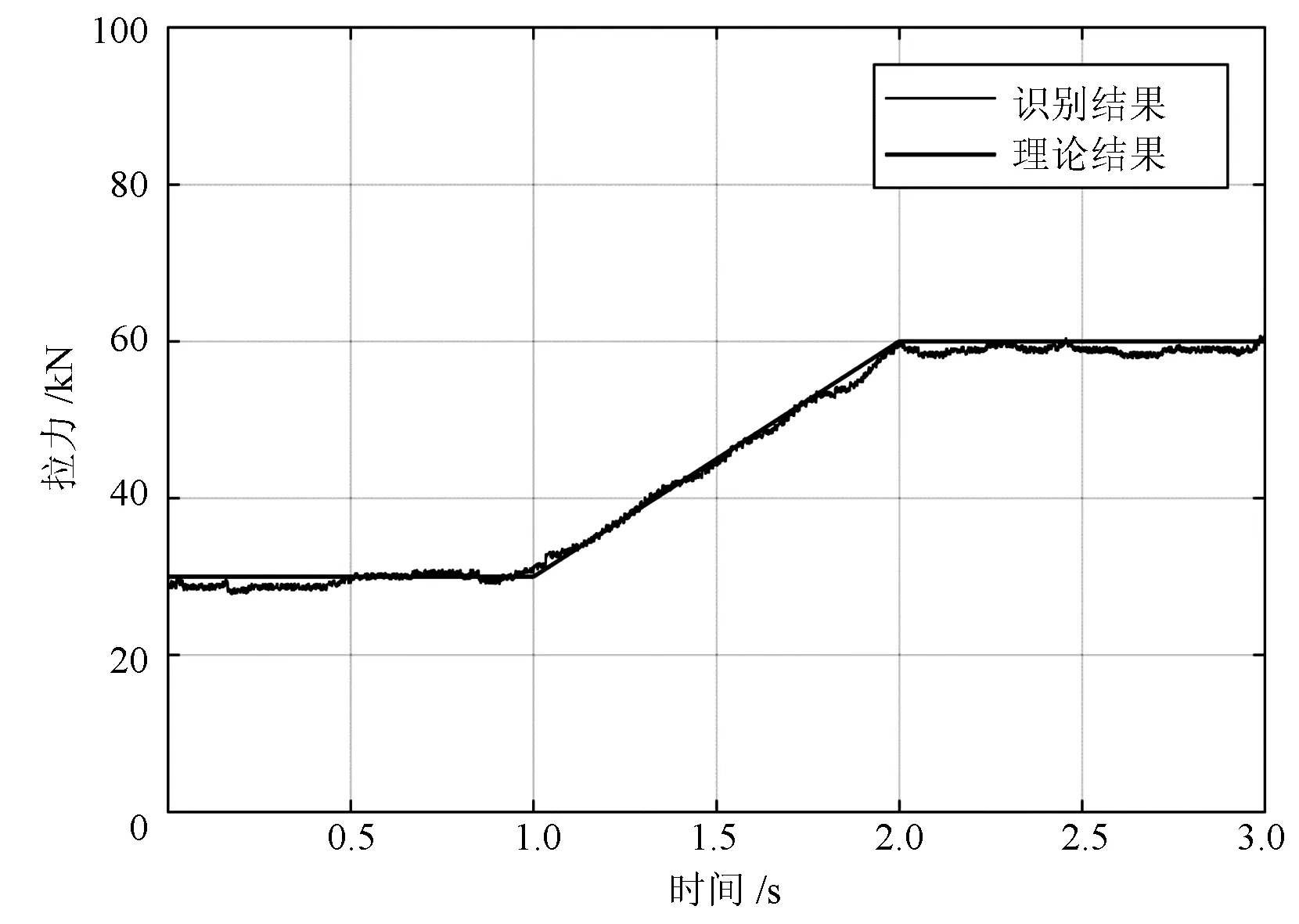
圖1 識別結果對比
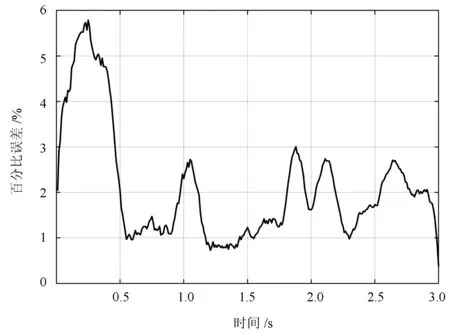
圖2 索力識別誤差
通過上述仿真模型的結果可知,索力的變化會影響索的固有頻率的大小,通過廣義S變換的時頻譜進行脊線提取,能夠有效地對索的一階瞬時頻率進行識別,從而實時地獲取時變索力。
4 結束語
針對傳統基于頻率法的索力識別方法只能識別索在過去一段時間內的平均索力,無法對索力進行實時的識別的問題,將廣義S變換方法應用于時變索力的識別。在仿真條件下,通過對索的振動加速度響應信號進行廣義S變換計算,然后通過時頻譜進行脊線提取,能夠有效地對索的一階瞬時頻率進行識別,從而實時獲取時變索力。仿真分析結果表明,廣義S變換方法對時變索力有較好的識別效果。

