極地海洋工程裝備平板構件的對流換熱影響分析

操太春 吳剛 孔祥逸 于東瑋 吳琳 張大勇

研究論文

極地海洋工程裝備平板構件的對流換熱影響分析

操太春1,3吳剛2孔祥逸1于東瑋1,3吳琳1張大勇1

(1大連理工大學海洋科學與技術學院, 遼寧 盤錦 124221;2中國船舶工業集團公司第七○八研究所, 上海 200021;3大連理工大學運載工程與力學學部, 遼寧 大連 116023)

電伴熱是極地海洋工程裝備防寒主要措施, 熱平衡是對流換熱的關鍵問題。本文以平板構件為研究對象, 采用數值模擬和模型試驗相結合的方法, 開展極地復雜環境因素對海洋工程裝備電加熱平板構件熱平衡影響分析。首先選取風速、溫度為主要環境參數, 風速為0～40m·s–1、溫度為–40～0℃, 基于Fluent仿真和試驗測試獲得電加熱平板構件在不同風速、溫度下的對流換熱系數。結果表明: 增大風速和降低溫度都會使平板的對流換熱系數增大, 在風速一定的情況下, 溫度對平板的換熱影響較小; 在溫度一定的情況下, 平板的對流換熱系數隨著風速的增加而顯著增大。最后, 基于試驗數據建立了電加熱平板構件的對流換熱系數數學預測模型, 并采用數值模擬驗證了該模型的正確性。

極地 平板構件 對流換熱 實驗測試 數值模擬

0 引言

極地海洋工程裝備是極地資源探測開發的主要載體, 然而受極端低溫、潮濕環境影響, 裝備極易發生結冰現象。結冰增加的重量不僅會降低結構穩定性、改變結構應力, 還可能影響工程設備的正常運行[1]。平板構件作為極地海洋工程裝備中的典型構件, 例如甲板、艙壁等, 其防寒措施一般采用伴熱方式。

伴熱有兩類加熱方式, 分別為恒壁溫加熱和恒熱流加熱。恒壁溫加熱的壁面溫度保持恒定; 恒熱流加熱以恒定的熱流量輸入, 當沒有熱量損失時, 壁面溫度將持續升高。因此這兩種加熱方式存在較大差別, 而極地工程裝備的電伴熱屬于恒熱流加熱。目前, 極區海洋工程裝備的防寒設計普遍參考船級社的相關規范[2], 由于對工程環境條件考慮較少[3], 實際運行過程中存在電伴熱的給熱量不合理問題[4-6], 在保證防寒效果的同時極易造成加熱能量的浪費, 給極地工程裝備的電力系統造成額外負擔。

目前, 平板的熱平衡研究主要集中在恒壁溫加熱, Churchill[7]基于理論和實驗分析, 提出了恒壁溫加熱條件下平板的平均努塞爾數()、局部關于普朗特數()與雷諾數()的表達式, 并明確各參數的取值。Junkhan等[8]研究了不同壓力梯度下湍流度對平板換熱的影響, 在層流換熱范圍內主流中湍流的作用不大, 但在湍流換熱范圍內, 傳熱系數隨湍流度的增大而增大。Whitaker[9]對層流邊界層及湍流邊界層的局部表達式進行了修正, 確定了平均; 研究發現采用簡單的函數關系來描述平板的對流換熱過程會存在一定誤差。Luikov等[10]研究了平板在恒壁溫條件下的邊界層及熱量交換機制, 給出了低普朗特數、速度分布和溫度分布的解析解。

然而, 極地裝備保溫系統采用的電加熱屬于恒熱流加熱方式, 現階段, 平板構件在電加熱條件下的對流換熱研究相對缺乏。Trevi?o等[11]研究了平板在對流條件下的穩態和瞬態加熱過程, 得到了平板在恒熱流加熱條件下縱向位置的溫度變化規律。Brazil等[5]研究了平板在不同溫度、不同風速下的熱量損失, 發現較大的表面積導致的熱損失超過船級社規范近50%。因此, 對于極地海洋工程裝備的防寒系統的設計不能完全參照船級社的規范, 同時應該考慮外部環境變化所帶來的影響。張雷等[12]對船舶在極區的運行工況進行研究, 分析了甲板除冰系統設計要點、計算方法以及相關的規范, 提出了極地船甲板除冰系統的設計方法。

可見, 加熱方式對平板構件的對流換熱影響顯著, 目前電加熱方式下的換熱規律還不是很明確, 理論計算還存在較大誤差。因此, 亟需建立平板構件的對流換熱系數預測模型, 為極地海洋工程裝備防寒設計提供參考。本文采用實驗結合Fluent仿真的方法, 對電加熱平板構件的對流換熱進行了研究分析。實驗研究了溫度范圍–40～0℃、風速范圍0～13.7 m·s–1的對流換熱系數隨溫度以及風速的變化規律, 并提出了對流換熱系數的擬合計算公式。通過數值仿真驗證了擬合公式在溫度范圍–40～0℃、風速范圍0～40m·s–1內的適用性。

1 平板的對流換熱要素分析

由牛頓冷卻公式可知, 平板的局部對流換熱系數可以表示為:

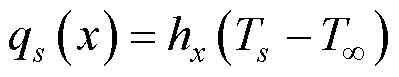
電加熱條件下, 平板的熱流通量是給定的額定量, 此時壁面溫度分布為[13]:

對于層流段

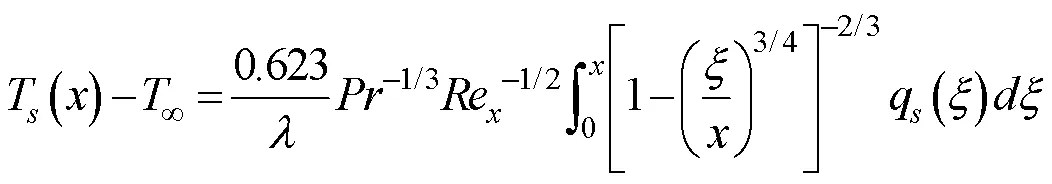
對于湍流段

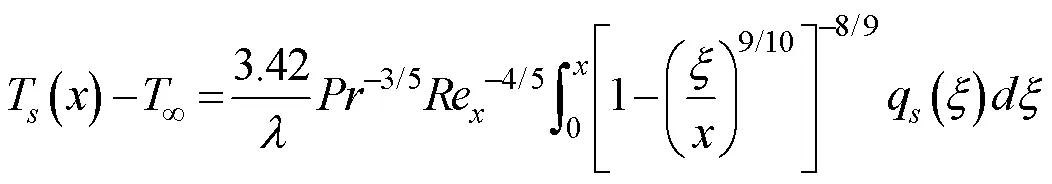
層流段局部表面傳熱系數

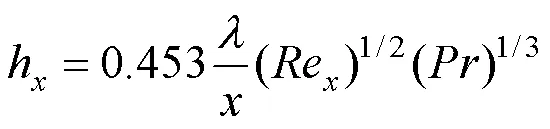
湍流段局部表面傳熱系數

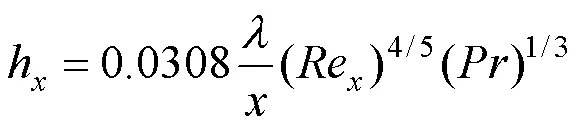
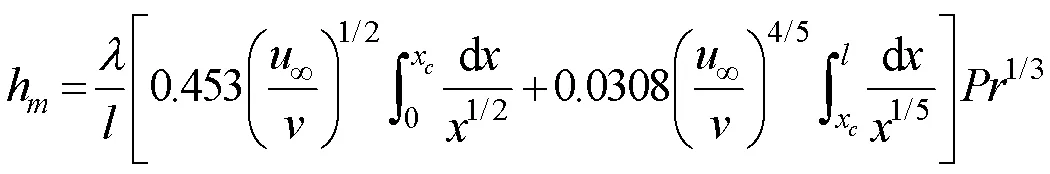
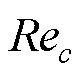
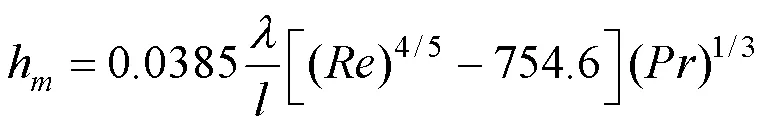
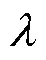
2 電加熱平板的對流換熱實驗

在低溫實驗室, 搭建了面向極地環境條件下的海洋工程裝備平板構件對流換熱實驗平臺, 實現了平板構件在不同風速、溫度條件下對流換熱系數的準確測定。低溫實驗室可控調節最低溫度為–50℃, 最大風速為15 m·s–1, 基本可以模擬極地的低溫環境。平板的對流換熱涉及層流段、過渡段和湍流段, 為充分考慮對流換熱不同階段產生的影響, 實驗選取的平板構件長2.4 m、寬0.7 m。

2.1 實驗系統

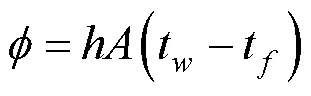
由此可得,

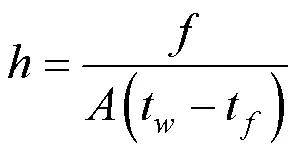
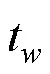
2.2 實驗結果分析

在低溫實驗室進行了24組平板對流換熱實驗, 實驗工況設置及實驗結果如表2所示。

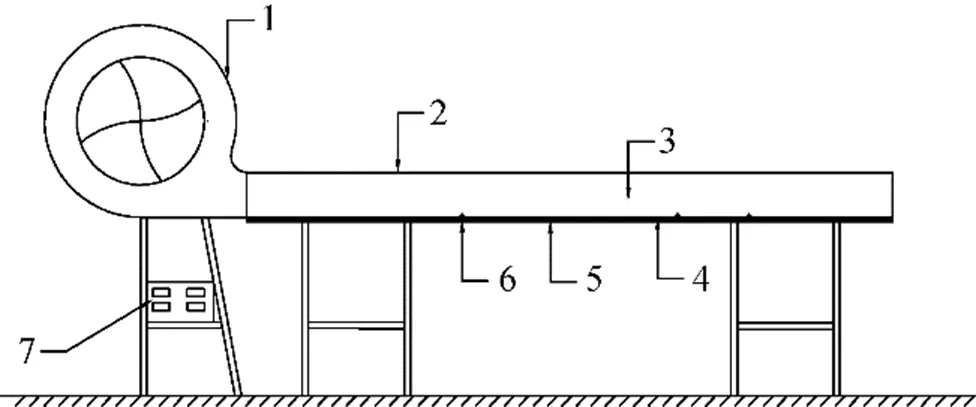
圖1 實驗裝置.1: 變頻風機, 2: 風罩, 3: 風道, 4: 實驗平板, 5: 加熱絲及保溫層, 6: 實驗平板上的測點, 7: 控制箱

Fig.1.Experimental apparatus.1: converter fan, 2: air hood, 3: air flow tunnel, 4: experimental plate, 5: heating wire and insulation layer, 6: measuring points on experimental plate, 7: control box

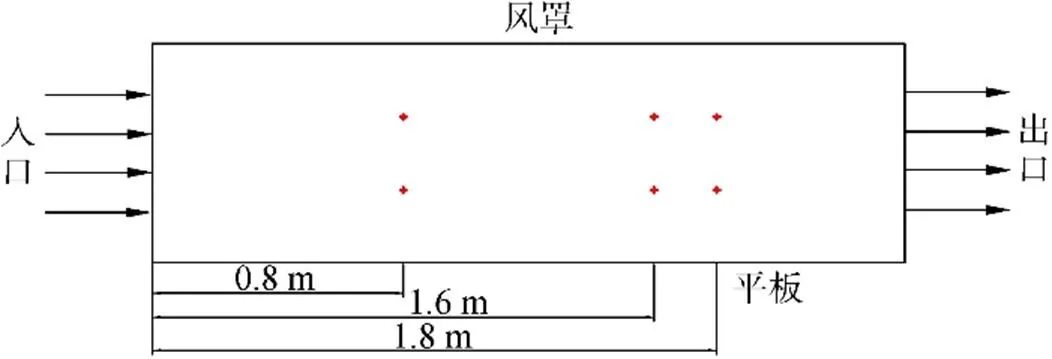
圖2 測點位置布置圖

Fig.2.Arrangement of measurement location

表1 實驗測量裝置

對流換熱系數的實測值誤差主要包含兩方面。(1)實驗測量的平板溫度和風溫在±0.1℃范圍內波動, 測量溫度的PT100傳感器的精度為±0.1℃。(2)實驗數據的處理方法：為減小實驗測量誤差, 每組實驗工況進行3次，考慮過渡段的影響, 數據處理時取整個平板的平均溫度計算對流換熱系數。

選取風速相近的實驗測量數據進行溫度對換熱系數的影響分析, 其結果如圖3所示。由圖可知, 平板對流換熱系數實測結果大于理論計算值, 在溫度為–20℃左右時, 實測值比其他溫度下的實測值偏小, 主要原因為該溫度下的實驗風速相對較小, 對流換熱系數隨溫度變化影響很小。可以認為, 在風速一定的情況下, 溫度對平板的換熱基本沒有影響。

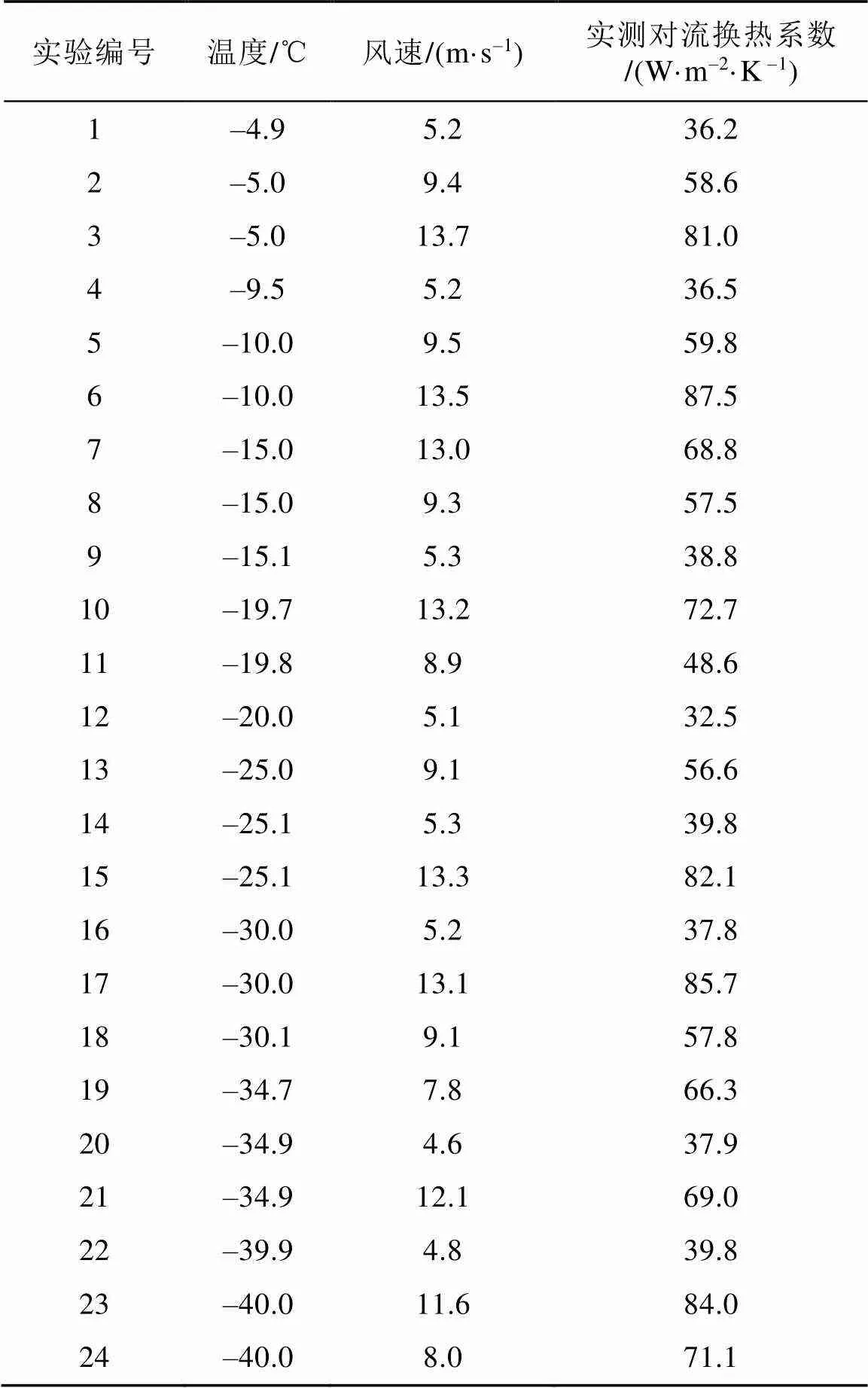
表2 實驗工況及結果

為了明確風速對平板對流換熱的影響, 本文將溫度較為接近的實驗工況下實測數據對比分析, 平板對流換熱系數隨著溫度變化情況如圖4所示。由圖可知, 平板對流換熱系數實測結果大于理論值, 在溫度一定的情況下, 平板的對流換熱系數隨著風速的增加而顯著增大, 可以認為在特定溫度下, 風速是影響平板換熱的主要因素。

2.3 基于實驗的平板對流換熱系數預測模型

從以上分析發現, 加熱平板對流換熱系數的實驗結果要大于理論值, 在一定程度上說明理論推導過程中只考慮層流段和湍流段的換熱是不合理的, 過渡段的影響不可忽視[14]。溫度一定時, 平板的對流換熱系數在風速范圍4.6～9.5 m·s–1內平均增大60.3%, 在風速范圍9.5～13.7m·s–1內平均增大45.4%; 風速一定時, 在溫度范圍–30～0℃內平均增大4.4%, 在溫度范圍–40～30℃內平均增大5.0%。因此, 風速是影響平板換熱的主要因素, 溫度對其影響很小, 受溫度影響的相關參數的變化范圍如表3所示。

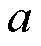
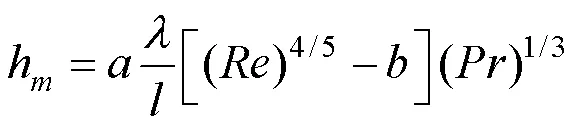
Fig.3.Variation of convective heat transfer coefficient with temperature.a) wind speed at 5.1–5.3 m·s–1; b) wind speed at 8.9– 9.5 m·s–1

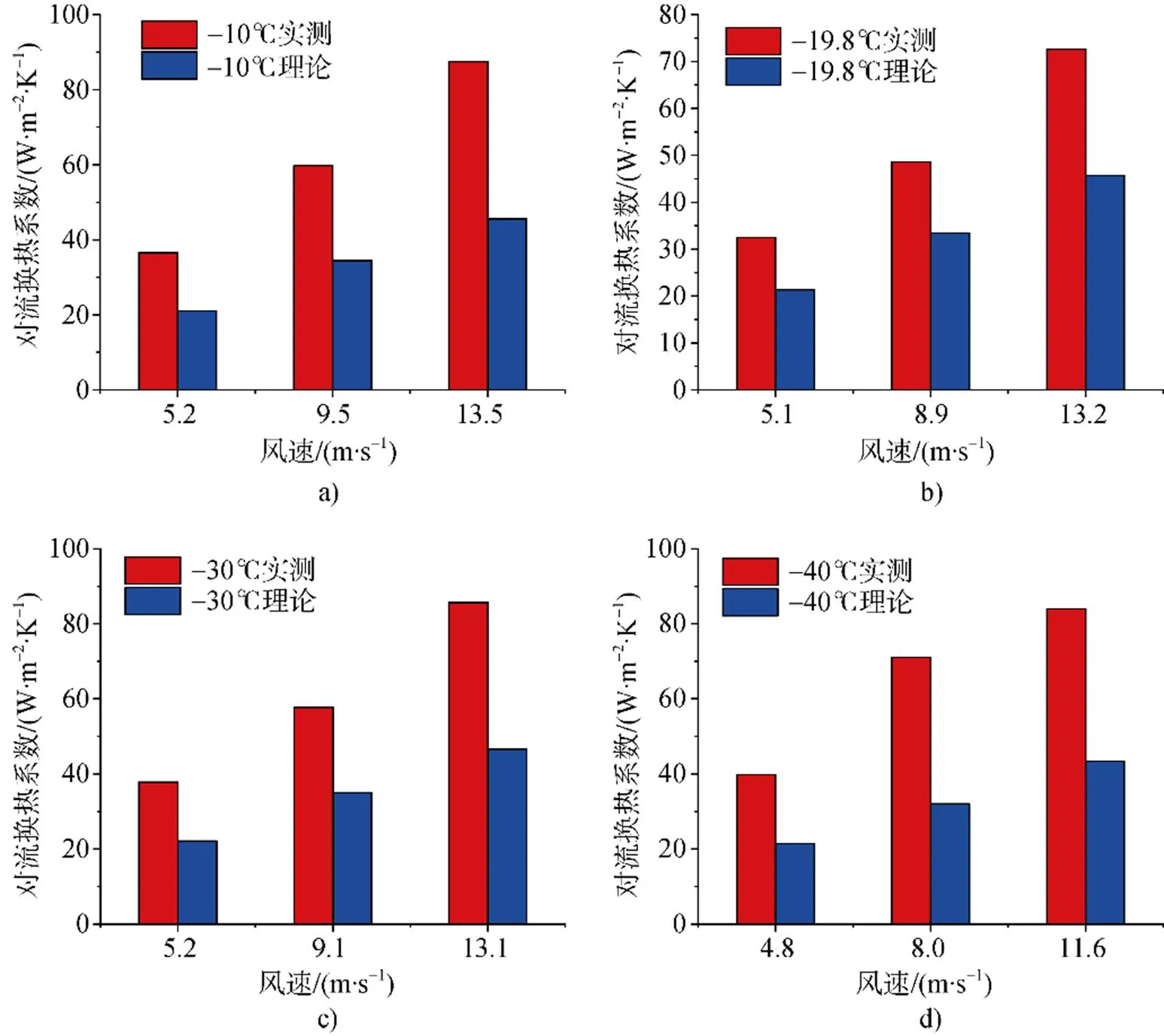
圖4 對流換熱系數隨著風速變化情況。a) 溫度為–10℃; b) 溫度為–19.8℃; c) 溫度為–30℃; d) 溫度為–40℃

Fig.4.Variation of convective heat transfer coefficient with wind speed.a) temperature at –10℃; b) temperature at –19.8℃; c) temperature at –30℃; d) temperature at –40℃

表3 普朗特數(Pr)與導熱系數(λ)的范圍

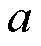
圖6比較了擬合公式與實測值的結果: 風速在5 m·s–1以及9 m·s–1左右時, 擬合公式和實測結果能夠非常好地接近, 其平均誤差為4.7%; 風速在13 m·s–1左右時, 誤差為6.0%, 驗證了擬合結果的正確性。

3 對流換熱系數的數值分析

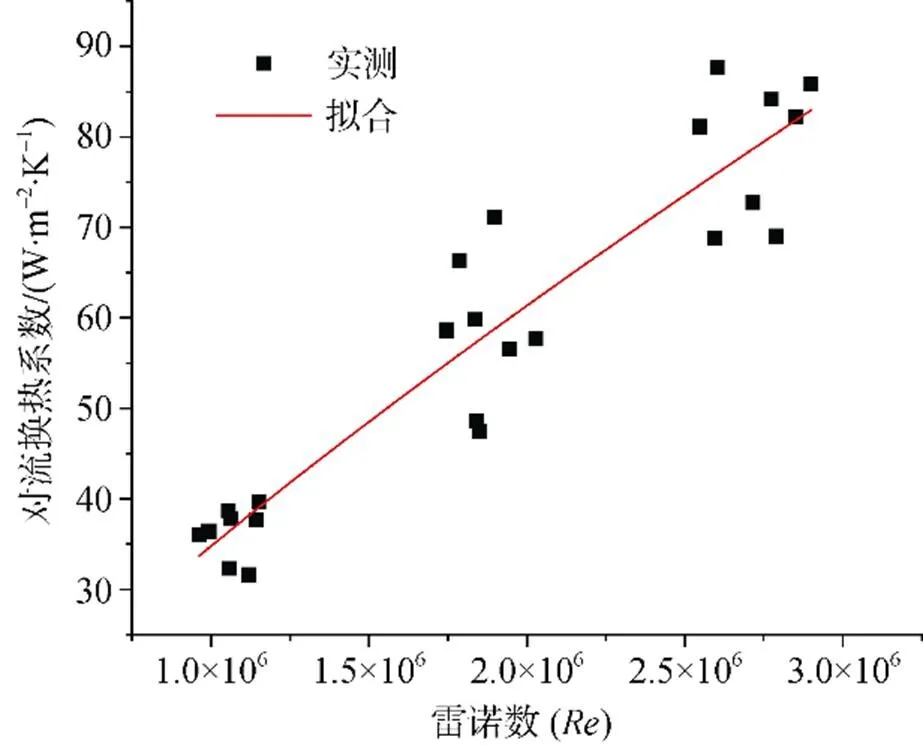
圖5 對流換熱系數實測數據擬合

Fig.5.Fitting of the measured data of convective heat transfer coefficients

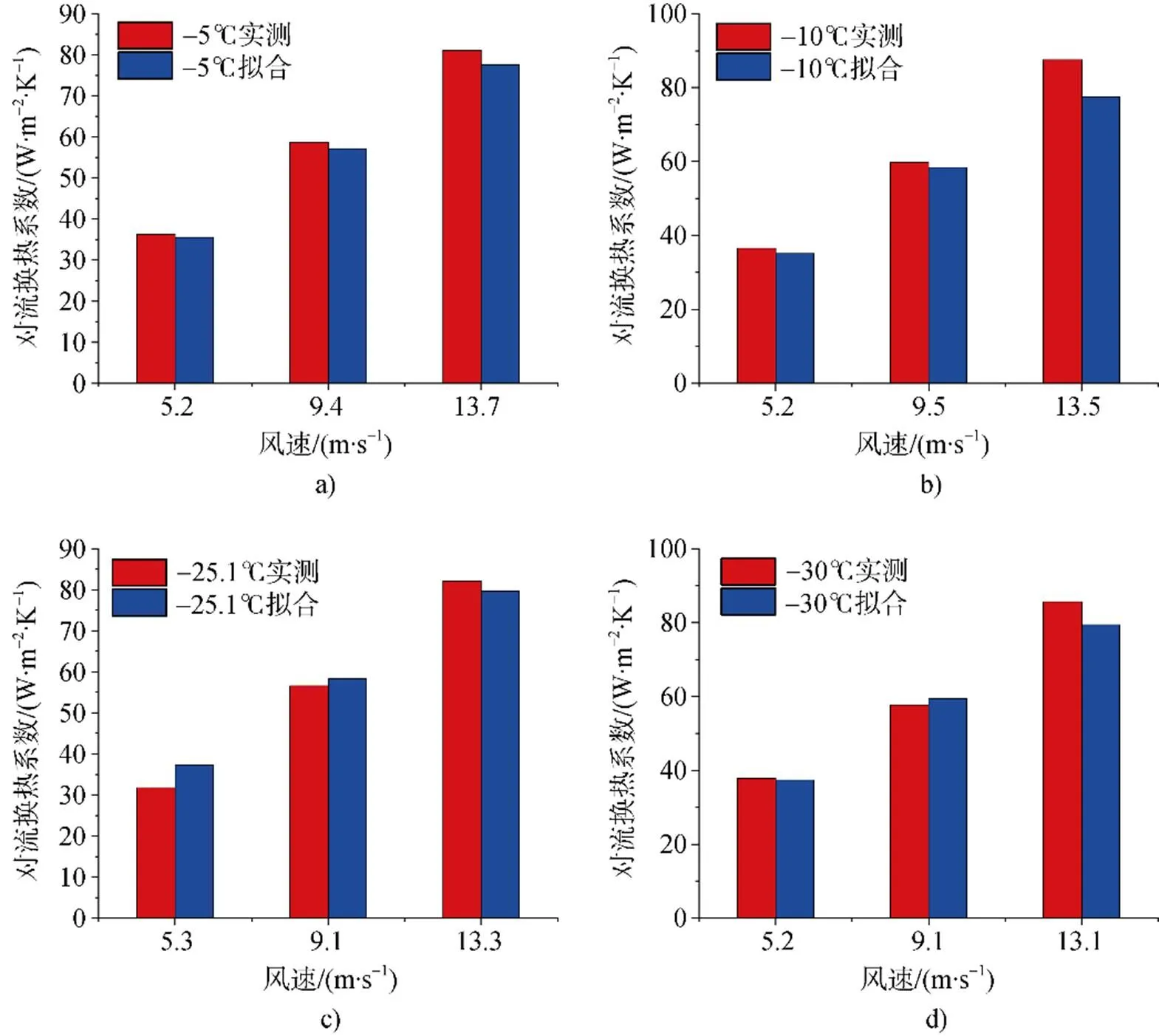
圖6 擬合與實測結果對比.a) 溫度為–5℃; b) 溫度為–10℃; c) 溫度為–25.1℃; d) 溫度為–30℃

Fig.6.Comparison between fitting and measured results.a) temperature at –5℃; b) temperature at –10℃; c) temperature at –25.1℃; d) temperature at –30℃

3.1 風速和溫度的影響分析

加熱平板對流換熱系數隨風速和溫度的變化如圖7和圖8所示。由圖7可知, 增大風速和降低溫度都會使平板的對流換熱系數增大, 并且風速比溫度對平板的對流換熱影響更加顯著。在風速小于25 m·s–1時, 溫度對平板的對流換熱系數影響很小; 當風速大于25 m·s–1時, 溫度對平板的對流換熱系數影響增大。由圖8可知, 溫差一定時, 不同風速下對流換熱系數增幅不同。風速大于25 m·s–1時, 對流換熱系數隨溫度變化的曲線斜率變大, 說明溫度對平板的對流換熱系數影響加大。

3.2 數值仿真與預測模型的對比分析

預測模型與數值仿真結果的對比如圖9所示。當風速小于20 m·s–1時, 預測模型與仿真結果吻合度較好, 其平均誤差為5.0%, 驗證了數值仿真模型的準確性。當風速大于20 m·s–1時, 模型預測值相較數值仿真結果偏大, 平均誤差為7.2%,滿足工程要求。由溫度影響分析可知, 在高風速時溫度的影響逐漸變大, 這也在一定程度上解釋了擬合結果在高風速時預測模型結果與仿真結果偏差增大。但是誤差分析表明在風速范圍0～40 m·s–1內, 所得平板對流換熱系數預測模型可為海洋工程裝備的平板熱平衡計算提供參考。

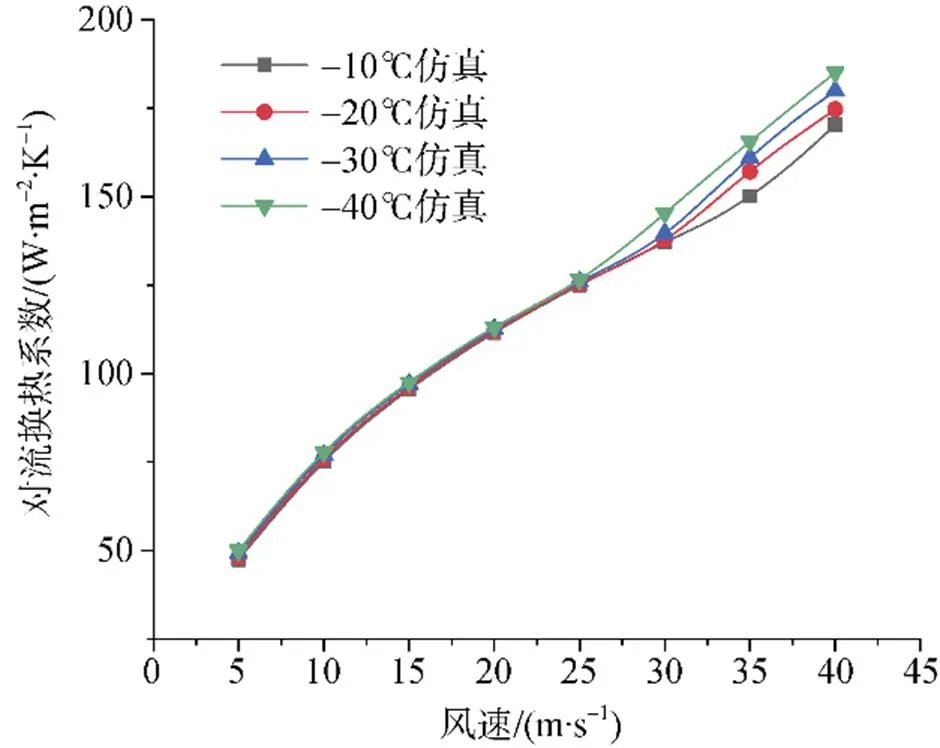
圖7 溫度–40～0℃下對流換熱系數隨風速變化

Fig.7.Variation of convective heat transfer coefficient at temperature (–40～0℃) with wind speed

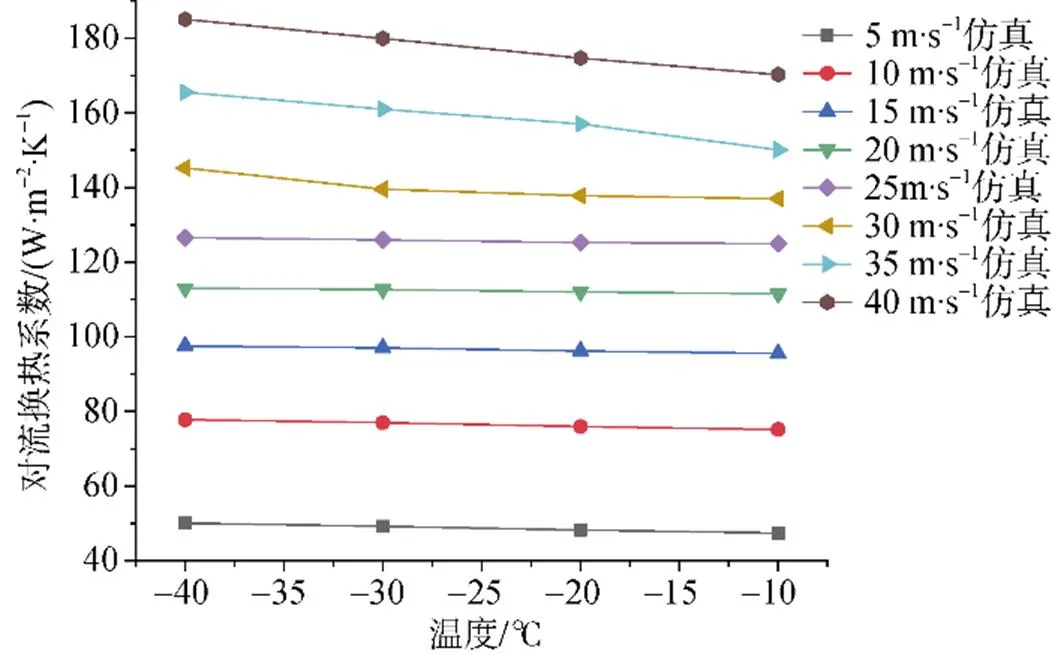
8 風速0～40 m·s–1下對流換熱系數隨溫度變化

Fig.8.Variation of convective heat transfer coefficient at wind speed (0～40 m·s–1) with temperature

4 結論

本文采用實驗測試和數值模擬相結合的方法, 對海洋工程裝備電加熱平板構件熱平衡影響分析開展研究。模型實驗中, 溫度范圍為–40～0℃、風速范圍為0～13.7 m·s–1, 結果表明: (1)平板對流換熱系數的實驗結果要大于理論值, 理論推導應該合理地考慮過渡段的影響; (2)增大風速和降低溫度都會使電加熱平板的對流換熱系數增大, 風速的影響更加顯著; (3)基于實驗獲得了平板對流換熱系數預測模型。

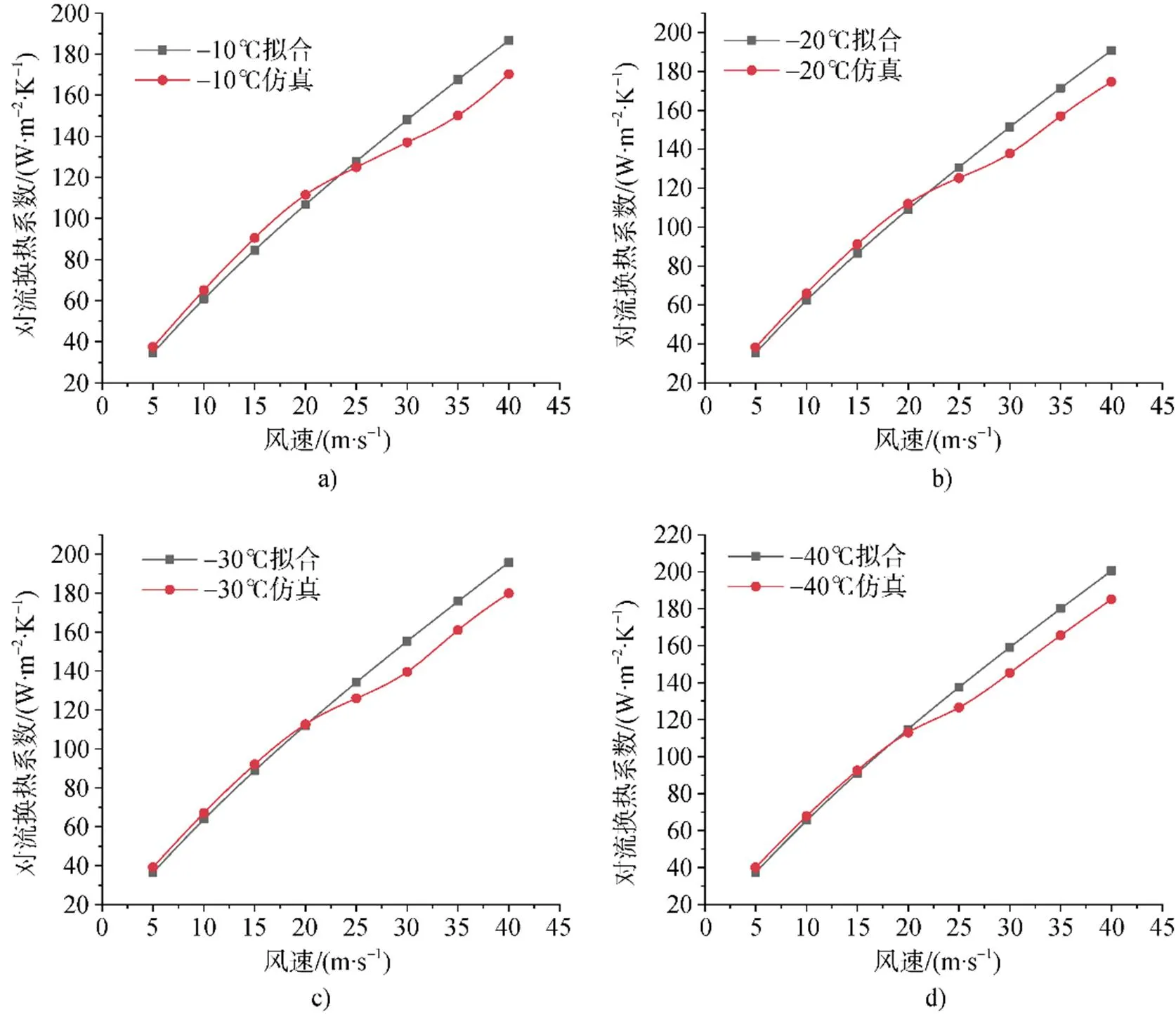
圖9 數值仿真與擬合結果對比.a) 溫度為–10℃; b) 溫度為–20℃; c) 溫度為–30℃; d) 溫度為–40℃

Fig.9.Comparison of numerical simulation and fitting results.a) temperature at –10℃; b) temperature at –20℃; c) temperature at–30℃; d) temperature –10℃

數值模擬對實驗條件不能達到的高風速工況進行了補充, 計算分析了風速在0～40 m·s–1范圍內電加熱平板的對流換熱系數, 結果表明: (1)增大風速和降低溫度都會增加平板的對流換熱系數, 風速影響顯著; (2)在風速小于25 m·s–1時, 溫度對平板的對流換熱系數影響很小; 當風速大于25 m·s–1時, 溫度對平板的對流換熱系數影響加大; (3)驗證了基于實驗獲得的對流換熱預測模型的適用性。

極地海洋工程裝備的構件類型眾多, 本文僅以平板構件為例開展電伴熱條件下對流換熱影響分析, 對于其他構件(例如扶手、踏步等)還需進一步開展研究。

1 沈杰, 白旭.基于Fluent和FENSAP-ICE的極區海洋平臺甲板結構結冰數值模擬[J].極地研究, 2020, 32(2): 177-183.

2 陳憲, 汪建華.極地船電加熱系統設計[J].廣船科技, 2015, 35(5): 5-9.

3 BAEN P, OLDFORD D.Surface heating for Arctic vessels and structures to prevent snow and ice accumulation[C]//2014 Petroleum and Chemical Industry Conference Europe.2014: 1-10.

4 ROEDER W, BAEN P, SEITZ R.Electric trace heat design methods for de-icing and anti-icing of vessels, support equipment and infrastructure in the Arctic[C]//Oceans.IEEE, 2017.

5 BRAZIL H, CONACHEY R, SAVAGE G, et al.Electrical heat tracing for surface heating on arctic vessels and structures to prevent snow and ice accumulation[J].IEEE Transactions on Industry Applications, 2013, 49(6): 2466-2470.

6 RYERSON C C.Ice protection of offshore platforms[J].Cold Regions Science and Technology, 2011, 65(1): 97-110.

7 CHURCHILL S W.A comprehensive correlating equation for forced convection from flat plates[J].AIChE Journal, 1976, 22(2): 264-268.

8 JUNKHAN G H, SEROVY G K.Effects of free-stream turbulence and pressure gradient on flat-plate boundary-layer velocity profiles and on heat transfer[J].Journal of Heat Transfer, 1967, 89(2): 169-175.

9 WHITAKER S.Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles[J].AIChE Journal, 1972, 18(2): 361-371.

10 LUIKOV A V, ALEKSASHENKO V A, ALEKSASHENKO A A.Analytical methods of solution of conjugated problems in convective heat transfer[J].International Journal of Heat and Mass Transfer, 1971, 14(8): 1047-1056.

11 TREVI?O C, LI?áN A.External heating of a flat plate in a convective flow[J].International Journal of Heat and Mass Transfer, 1984, 27(7): 1067-1073.

12 張雷, 伍蓉暉, 陳方紅, 等.極地船甲板除冰系統設計[J].廣東造船, 2019, 38(1): 58-60.

13 INCROPERA F P, DEWITT D P.Fundamentals of heat and mass transfer[M].5th ed.New York: John Wiley & Sons, 2001: 389-395.

14 LIENHARD J H.Heat transfer in flat-plate boundary layers: A correlation for laminar, transitional, and turbulent flow[J].Journal of Heat Transfer, 2020,142(6):061805.

Analysis on the influence of convective heat transfer of polar ocean engineering equipment plate components

Cao Taichun1,3, Wu Gang2, Kong Xiangyi1, Yu Dongwei1,3, Wu Lin1, Zhang Dayong1

(1College of Marine Science and Technology, Dalian University of Technology, Panjin 124221, China;2Marine Design and Research Institute of China, Shanghai 200021, China;3Department of Carrier Engineering and Mechanics, Dalian University of Technology, Dalian 116023, China)

The electric-heat method is the main cold-proof measure for polar ocean engineering equipment, with thermal balance being key to convective heat transfer.Taking an electric heading plate component as a research object, numerical simulations and model tests were carried out to analyze the influence of complex polar environmental factors on the thermal balance of electric heating of marine engineering equipment.Wind speed and temperature were considered as the main environmental parameters in this analysis; wind speed was varied over the range 0–40 m·s–1and temperature over the range ?40–0 °C.Based on FLUENT software simulations and model tests, the convective heat transfer coefficients of the electrical heating plate component under different wind speeds and temperatures were obtained.The results showed that increasing wind speed and decreasing temperature could increase the convective heat transfer coefficient of the plate component.Temperature had little effect on the heat transfer of the plate when the wind speed was stable.In contrast, the convective heat transfer coefficient of the plate increased significantly with increasing wind speed at a given temperature.A mathematical prediction model for the convective heat transfer coefficient of the electrical heating plate component was established based on these experimental data, and the validity of the model was verified by numerical simulation.

polar region, flat plate member, convective heat transfer, experimental testing, numerical simulation

2020年12月收到來稿, 2021年3月收到修改稿

國家自然科學基金(52071055)、遼寧省高等學校創新團隊(LT2019004)資助

操太春, 男, 1995年生。碩士研究生, 主要從事海洋工程裝備防寒研究。E-mail: caotaichun@foxmail.com

張大勇, E-mail: zhangdy@dlut.edu.cn

10.13679/j.jdyj.20200080