基于VSG_MPC的儲能換流器調頻控制策略

尹 山， 董建園

(西安建筑科技大學機電工程學院，陜西西安710055)

在新能源大規模并網的當下，傳統調頻方式已不能滿足未來智能電網的調頻需求，而電池儲能技術以其優秀的功率響應能力使其成為現階段電網調頻輔助手段的研究熱點。在儲能電池參與電網調頻研究中，當將其大規模接入電網時，由于并網逆變器缺少像同步發電機應對電網擾動的那種很強的魯棒性而不能實現調頻調壓[1]，所以有學者提出了虛擬同步發電機(virtual synchronous generator，VSG)技術。虛擬同步發電機(VSG)技術是在同步發電機外特性基礎上進行模擬的，因此其不僅具備同步發電機所具有的阻尼能力，也具備慣性，在這種條件下，可有效改善并網點的電壓強度[2]。由于VSG 的上述優點，尤其是在模擬同步發電機參與電網調頻方面的突出表現，本文考慮到面向電網調頻的需求，選擇VSG 控制策略作為儲能變流器(power conversion system，PCS)的有功頻率上層控制；又因為模型預測控制(model predictive control，MPC)算法具有可在線優化能減少對模型精度依賴方面的獨特優勢，以及具有自適應性和穩定性等特性，故而在電力電子領域得到了廣泛的應用，尤其是在儲能并網逆變器控制策略中。因此本文同時考慮到PCS 需要適應電網中不同的工況，特別是功率響應的范圍由W～kW～MW的變化，需要在較短時間內對頻率的變化做出快速響應，因此考慮采用MPC 作為下層的控制策略，代替傳統的電壓電流雙閉環PI 控制。

1 雙向儲能換流器的基本工作原理及其數學模型

為后續研究的便捷性，將PCS 的直流側等效為直流源，要建立三相VSC 的數學模型必須以三相電壓源型換流器的拓撲結構為主要依據[3]，按照電路相關知識，組建KCL，KVL方程[4]，并做出以下假設，即理想電網、理想電源、理想元器件、無阻抗的導線。由于前級的Buck-Boost 電路僅作為維持直流母線電壓穩定的作用，因此主要分析VSC 雙向換流器的數學模型及其控制策略。

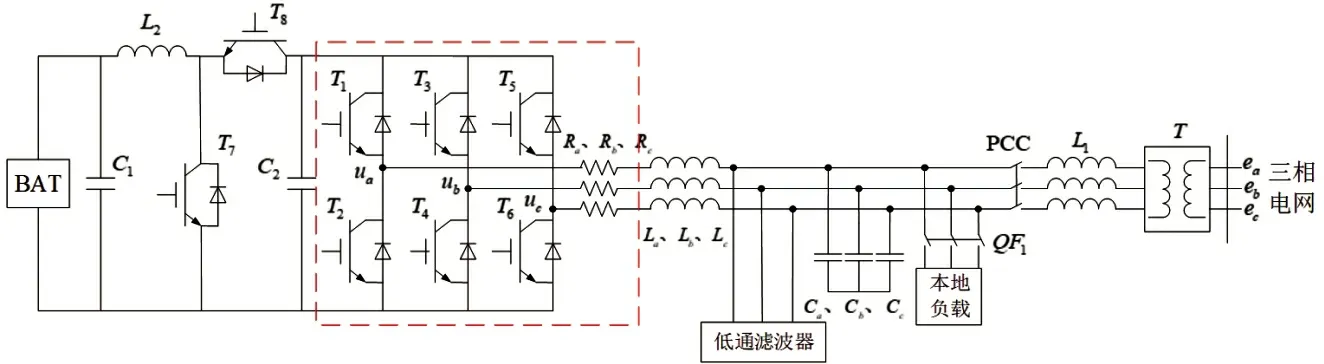
圖1 PCS 主電路圖

圖1 中的逆變器橋臂側端等效電壓分別用ua、ub、uc來表示；電網的電動勢分別用ea、eb、ec表示；La、Lb、Lc為濾波電感表示符，其數值等于5 mH；逆變器線路電感和開關管的等效電阻的數值為0.5 Ω，并分別用Ra、Rb、Rc表示，最后用Ca、Cb、Cc表示濾波電容，電容值為40μF，直流側電壓為700 V。

結合以上分析，在Matlab/Simulink 仿真平臺上搭建儲能電池的仿真模型，如圖2 所示[5]。其中，儲能電池組的額定容量為40 Ah，額定出口電壓為200 V，雙向DC/DC 電路的參數為：L=0.001 H，C=0.001 F。對于前級的Buck-Boost 電路(見圖3)，采用電壓電流雙閉環控制策略，以此達到升壓的目的，維持直流母線電壓的穩定[6]。

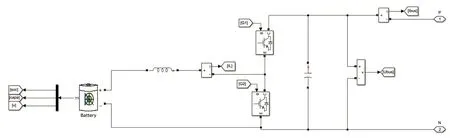
圖2 前級電路等效模型

圖3 蓄電池恒壓充放電控制算法示意圖

圖3 中，Ubref和Ibref表示儲能電池出口的給定電壓和給定電流，Ubar、Ibar為儲能電池出口的實測電壓和電流，電壓環PI控制器的參數Kpv=10、Kiv=100，電流環PI 控制器的參數Kpi=5、Kii=20。

參考圖1 所示PCS 主電路的虛線拓撲三相兩電平電路模型以及在其三相a，b，c 靜止坐標系下建立的數學模型，通過Clark 變換，可得到其兩相αβ 靜止坐標系下的數學模型，用式(1)表示：

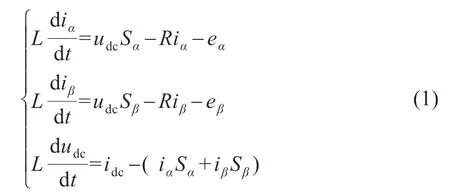
式中：Sα，Sβ分別為α、β坐標系中單極性二值邏輯開關函數值。

經過PARK 變換可得兩相旋轉坐標系下的數學模型為[7]：

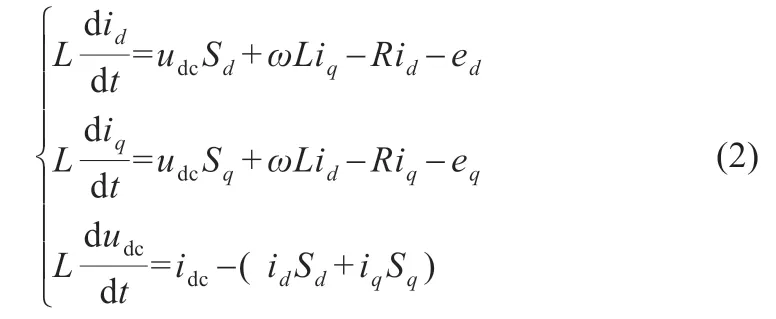
式中：Sd、Sq分別為dq 坐標系中單極性二值邏輯開關函數。

2 儲能變流器VSG 的拓撲結構與數學模型

儲能變流器VSG 的調節特性是指在模擬同步發電機中的一次頻率調整過程，當同步發電機的轉速波動時，其可以通過轉速調節器檢測轉速變化從而調整其機械功率的輸出大小，進一步通過電樞反應調節其發出的電磁功率，然后類比這一原理可以得到VSG 的有功-頻率控制方程：

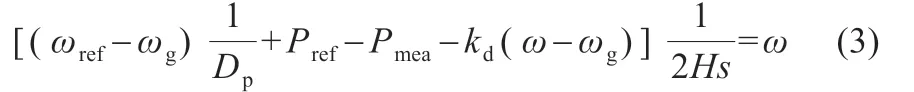
式中：H 為虛擬慣性時間常數；ω 為PCS 系統角頻率；ωg為公共母線角頻率；ωref為角頻率的參考值；Pref為有功功率設定值；Pmea為儲能換流器輸出有功測量值；kd為阻尼系數；Dp為有功功率的下垂系數；s 為拉普拉斯變換的復頻率。儲能變流器的VSG 一般由儲能電池系統、負載、雙向DC-AC 換流器及其控制單元組成，其結構拓撲見圖4。

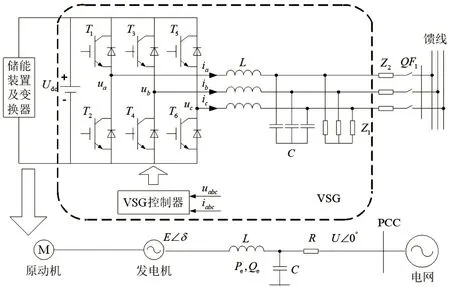
圖4 虛擬同步發電機結構示意圖

圖4 中，在儲能變流器VSG 模型中，將電池儲能裝置等效為原動機；將磷酸鐵鋰儲能裝置與雙向換流器等效為具有轉動慣量的同步發電機，通過調節VSG 無功得到虛擬同步發電機的暫態電勢，進而控制其輸出電壓U，當儲能變流器帶載或接入電網時，定子就會產生相應的電流I。

在本文中，選取同步發電機的二階數學方程模擬其電磁暫態過程以及轉矩調節過程，類比儲能雙向換流器，其輸出電抗可以等效為同步發電機的暫態電抗，電阻可以等效為定子繞組的阻值[7]，故其中儲能變流器VSG 的無功-電壓控制方程可以表示為：

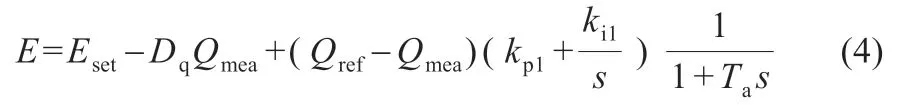
式中：Dq為無功功率的下垂系數；kp1、ki1為比例和積分系數；Ta為延遲環節的時間常數；Eset為VSG 機端電壓設定參考值；Qref為無功功率設定值；Qmea為逆變單元輸出無功功率測量值；E 為經VSG 控制算法得到的參考電壓幅值。

儲能變流器VSG 的機械特性可表示為[8]：

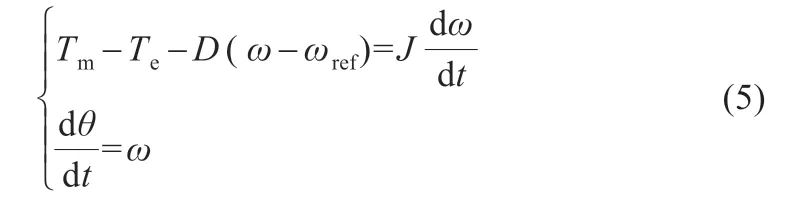
式中：Tm為VSG 電磁轉矩；Te為VSG 機械轉矩；D 為阻尼系數；ω 為轉子實際電角速度；ωref為額定電角速度；J 為轉動慣量。

3 基于VSG 的有功頻率外環控制策略

虛擬同步發電機的有功頻率控制器是模擬同步發電機的調速系統，利用轉子轉矩生成頻率的指令，通過調節頻率偏差可以減小功率偏差，其虛擬角速度可以由有功與頻率通過下垂控制獲得；虛擬同步發電機的無功電壓控制器是模擬同步發電機的勵磁系統[9]，勵磁調節模擬同步發電機的無功電壓下垂特性，輸出感性無功時，發電機機端電壓降低；吸收容性無功時，發電機機端電壓升高。圖5 所示為VSG 控制框圖。

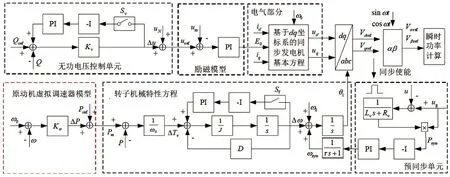
圖5 VSG控制框圖

圖5 中，D 為儲能變流器VSG 模擬的同步發電機阻尼系數，數值是20；J 為其轉動慣量，數值是4 kg/m2；θ1為虛擬轉子的角度，經求余之后得到虛擬角速度，電流矢量乘以sin ωt 得到q 軸電流，同理可得到d 軸電流，為下文的abc-dq 變換提供參考角度。

利用虛擬同步發電機模擬同步發電機進行調頻的過程，其中VSG 輸出的頻率主要受電磁轉矩與轉子角速度的影響[10]，當電網頻率升高時，雙向儲能換流器處于整流狀態，通過吸收電網中多余的電能達到減小頻率波動的目的。同理，當電網頻率跌落時，雙向儲能換流器處于逆變狀態，向電網輸送一定的功率來達到抑制頻率波動的目的，其中儲能換流器吸收和釋放功率的過程可模仿轉子動能的存儲與釋放過程[11]。通過控制虛擬同步發電機的電磁轉矩，使其跟隨機械轉矩的變化而變化。當虛擬同步發電機的Tm等于Te時，VSG輸出的Δf 等于零；當虛擬同步發電機的Tm大于Te時，VSG 輸出的Δf 大于零；當虛擬同步發電機的Tm小于Te時，VSG 輸出的Δf 小于零。圖6 所示為VSG 輸出有功功率與系統頻率的關系。

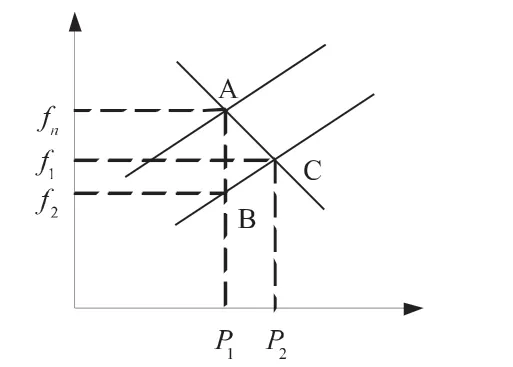
圖6 有功功率與頻率關系

由圖6 可知，當VSG 輸出的有功等于P1，頻率為fn=50 Hz 時，其處于穩定狀態A；當頻率跌落到f1時，根據下垂控制特性，其輸出的有功功率為P2，此時頻率將保持在f1不再變化；當系統負荷突減時，如果不經過調頻，系統頻率將會穩定在B 點[12]，此時系統的頻率為f2，通常將這個調速過程稱為一次調頻[13]。

傳統的虛擬同步發電機調頻過程模擬的是同步發電機的調頻過程，如圖7 所示。雖然VSG 能對系統頻率進行一定的調節，但是容易造成功率越限超調和轉子角來回振蕩，不利于系統的穩定。

將VSG 的調頻系數定義為kR，利用虛擬同步發電機的有功增量與頻率增量進行調頻，其表達式為：

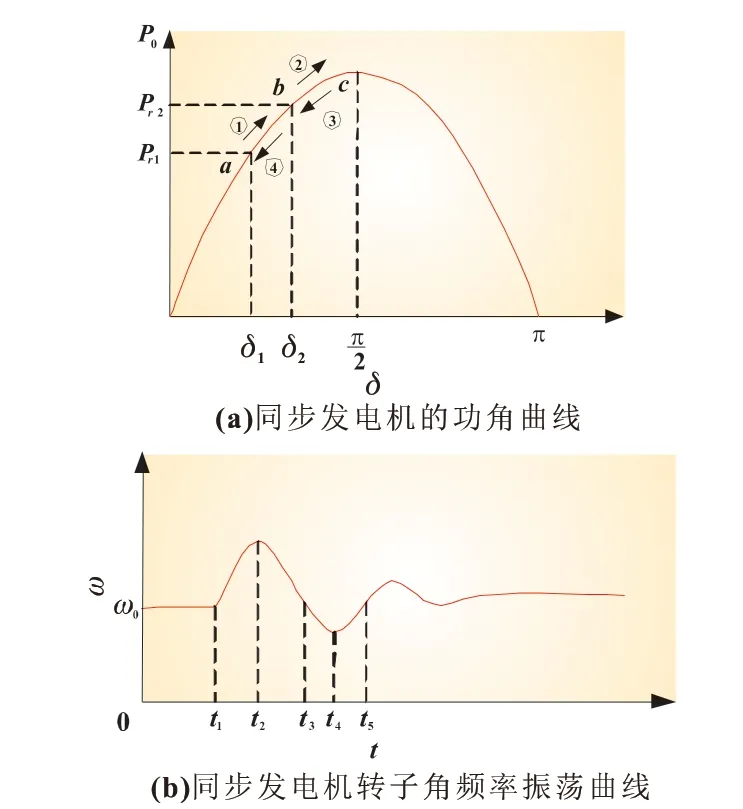
圖7 傳統同步發電機調頻過程

式中：fref為參考頻率值；fg為電網頻率值；P1與P2為調節前后的有功功率值。

當儲能系統并網發電運行時，若系統發生較小的擾動，由于儲能裝置慣性較小，會在瞬時發出或者吸收有功功率來彌補功率的偏差，完成對電網功率波動的平抑和抑制負荷擾動；若系統出現較大的擾動，利用VSG 控制，儲能快速響應系統頻率的波動，向系統輸出有功功率，對電網的頻率進行支撐；當超過系統調頻范圍時，需要減載運行，儲能系統進入孤島運行狀態[14]。

4 基于MPC 的三相并網逆變器直接功率預測內環控制策略

4.1 模型預測直接功率控制原理

基于瞬時功率控制理論，通過開關表判斷空間矢量所處的位置，進而選擇IGBT 的開關組合方式，但是，因其空間扇區劃分受限，使開關表中矢量選擇不夠準確，造成儲能逆變器輸出的電流和功率產生較大的波動，尤其當電網電壓出現較大波動時，可能會造成IGBT 過壓失效。在此基礎上，參考文獻[15]提出了模型預測直接功率控制策略，與傳統的直接功率控制DPC 相比省去了內部電流控制環，同時不需要添加外部的調制器，將控制過程與矢量調制融合為最優矢量的選擇，其控制目標多樣，可以選擇一個或多個與系統相關的電壓電流、有功無功、頻率等狀態量，調節其控制系數對不同的量進行優先調節，且控制過程比較直觀。在研究中已知αβ 坐標系下的電流量為正弦量處于不斷變化之中，那么在預測過程中，需要對電流ik下一時刻的采樣值ik+1進行預測，然而在此過程中，電流本身的預測就存在不穩定性，因此選擇系統穩定時的有功無功進行預測，在上述過程中有功無功為定值。故而僅需控制預測功率值與給定功率值盡量保持較小的誤差，此時用p 表示瞬時有功功率，用q 表示瞬時無功功率，那么其變化率可以表示為：

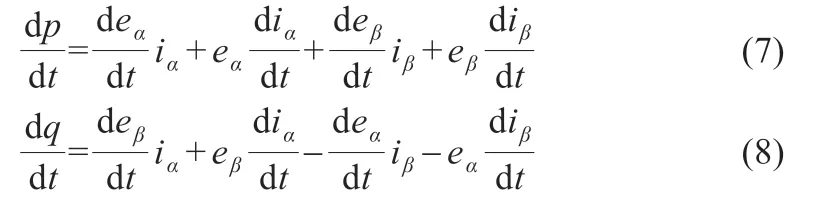
對于eα和eβ求導可得：

將式(9)和(10)的結果代入到式(7)與(8)中，得到有功功率與無功功率的變化率結果為：

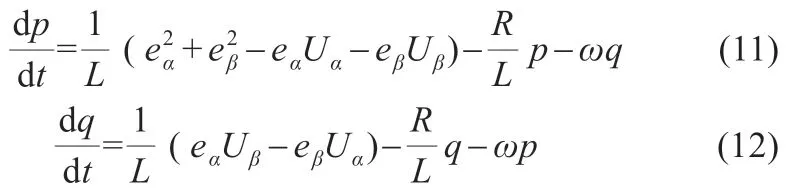
將第k 個采樣時刻的有功功率瞬時值記作p(k)，無功功率瞬時值記為q(k)，依照Euler 公式，可以得到在時刻k+1 時的有、無功功率的估計值為：

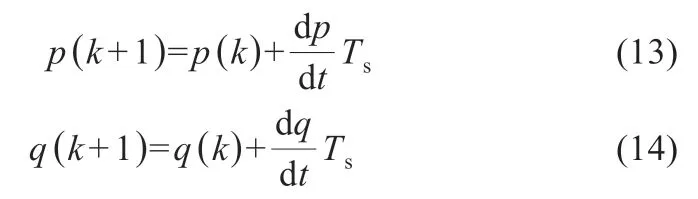
式(13)～(14)中：Ts為 儲 能 變 流 器IGBT 的 開 關 周 期 值；p(k+1)為有功功率在k+1 時得到的采樣數值，其數值大小與dp/dt 相關；q(k+1)為無功功率在k+1 時得到的采樣數值，其數值大小與dq/dt 相關。而根據式(11)、(12)可看出dp/dt 和dq/dt與Uα和Uβ之間存在直接的聯系，從而導致Uα和Uβ的值會影響k+1 時刻的有功無功功率變化。由于在式(2)中可以得出Uα和Uβ的變化只受Sd和Sq的影響，故而可以得到p(k+1)和q(k+1)與Sd和Sq之間存在密不可分的相關性。因此可知，下一周期的功率數值一定會隨著開關狀態的變化而發生一定的改變。

4.2 儲能變流器預測控制策略實施

如圖8 所示，通過測量αβ 坐標系下的電網電壓值e(k)和儲能逆變器輸出的電流值i(k)，經過模型預測得到第k+1 時刻的儲能逆變器輸出的電流值i(k+1)和電網電壓值e(k+1)，再根據αβ 坐標系下的瞬時有功功率計算公式，可以對下一時刻儲能逆變器輸出的有功功率p(k+1)和無功功率q(k+1)進行計算[16]。由于代價函數設置為功率值的偏差，因此可以對每一個求得的功率值進行評估，將得到的最優矢量進行存儲，從而應用最優矢量Ur進行調制。

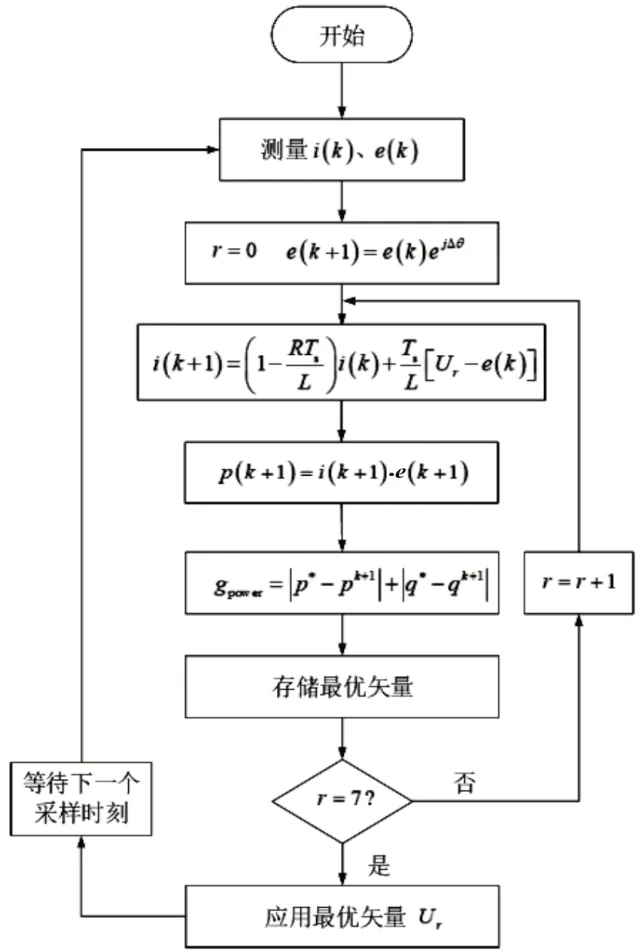
圖8 模型預測功率控制流程圖

通過模型預測可以得到在αβ 坐標系下儲能逆變器下一時刻輸出的交流電流與交流電壓值，而此數值可以通過式(1)計算得到。在前面分析的基礎上可知，儲能逆變器的開關狀態共分為八類，這八類開關狀態要求在預測電流時必須每個狀態都要重新計算一次[17]，而通過矢量角補償可以得到其交流電壓值，因此將αβ 坐標系下的電壓電流的微分方程進行離散化得到電壓電流差分方程，如式(15)：

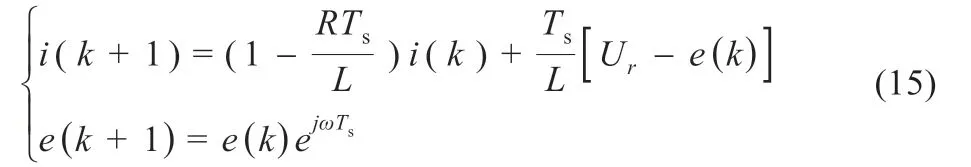
通過上面分析即可得到交流電流與電壓值，利用瞬時功率計算公式可求出儲能逆變器預測的瞬時功率值，將直接功率控制下的有功和無功功率進行離散化，則預測的瞬時功率如式(16)所示：

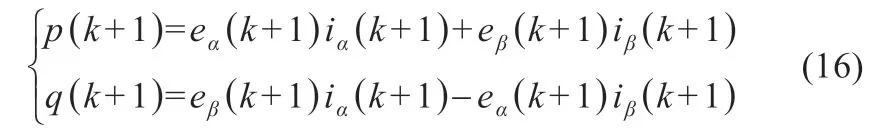
由式(16)可得到有功功率預測值為p(k+1)，無功功率預測值為q(k+1)，且將以上兩個預測功率值代入式(17)中，可得到代價函數gpower的值。通過計算可得到與儲能逆變器的八類開關狀態所對應的八個代價函數。選取最小的gpower值，將使gpower最小的電壓矢量值應用在下一周期，可使下一采樣周期的有功功率和無功功率更加趨近于給定的參考數值。綜上所述，可知代價函數gpower可保證最大限度降低儲能逆變器輸出的有功無功功率誤差，有效控制有功功率p，使其和p*值基本一致。

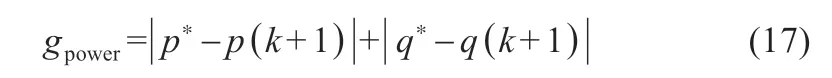
在儲能逆變器正常運行時，需保證其采樣周期是固定不變的，且在所有的采樣間隔內，其開關狀態要恒定。在每次采樣間隔中，控制策略以最小化代價函數為基準，選出最合適的電壓矢量[18]。模型預測直接功率控制條件不多，沒有繁瑣的內環控制與外環調制，其只需跟蹤有功與無功功率，便可實現其控制目的。通常來講，無功功率q*的最佳設定值為0，在此設定值基礎上，取得單位功率因數運行。

5 基于VSG_MPC 的PCS 參與電網調頻綜合控制策略

在前述的基礎上，在前述的基礎上，本文提出了面向電網調頻的儲能換流器VSG_MPC 控制策略，其控制原理框圖9所示。在本文中，可將電網等效為恒定的電壓源，模擬并入大電網的電壓和頻率特性。當VSG 離網運行時，運行于VF模式，當VSG 并網運行時，根據給定的有功無功指令向電網輸送功率，可等效為受控電流源，運行于PQ 模式。圖中，Vabc、Iabc為電網側的電壓和電流；ILabc為雙向儲能換流器輸出的電流；sin ωt - cos ωt 由圖5 所示的VSG 控制部分計算所得；E0、ω0分別為電網電壓的相電壓基波峰值和基波頻率[19]。

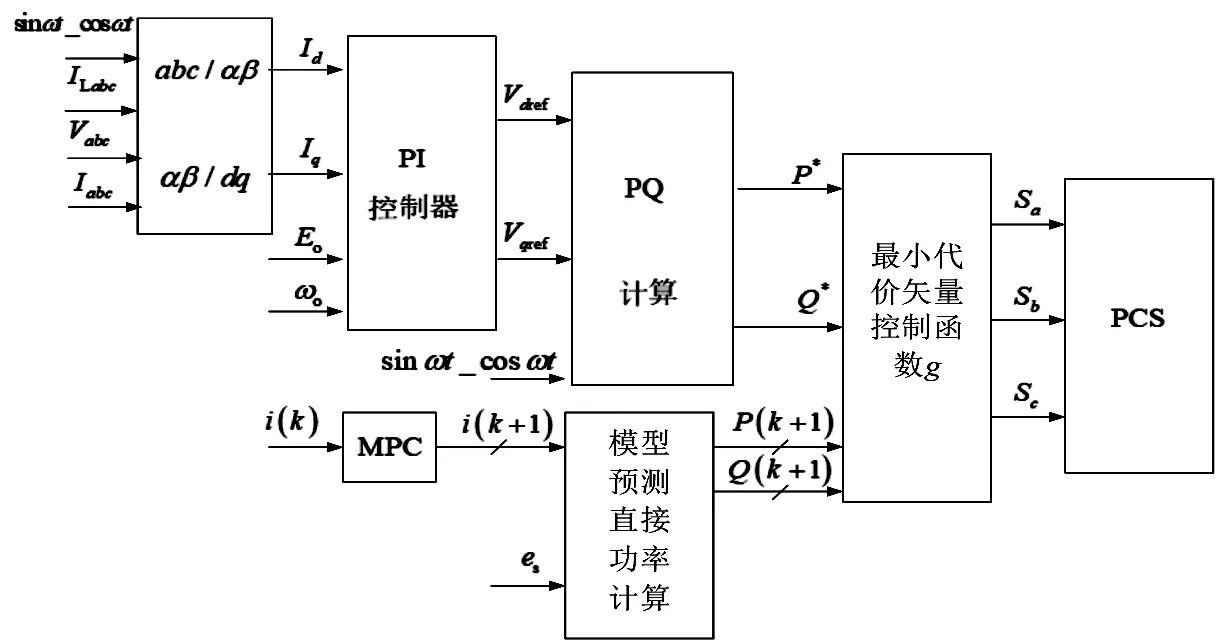
圖9 VSG-MPC控制策略

為了進一步證明本控制策略的有效性，構建了系統在并網運行時的小信號模型。圖10 為VSG 并網的拓撲結構。圖中，VSG 的輸出電壓為E ＜φ，電網電壓為Ug＜0，線路等效阻抗為R1+ jX1，Ig為線路電流。

圖10 VSG的并網拓撲結構

并網運行時，VSG 所輸出的復功率S 的表達式為：

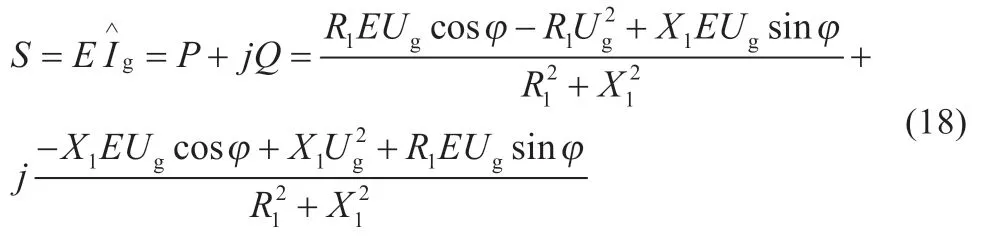
則系統傳輸的有功和無功的小信號模型分別為：

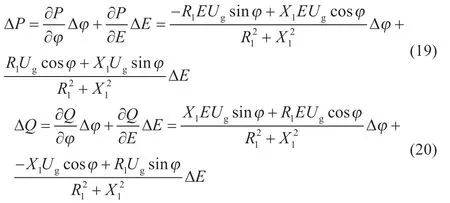
當系統處于并網狀態下有ωg=ωref，將(19)、(20)聯立可推導出儲能換流器控制小信號模型如下：

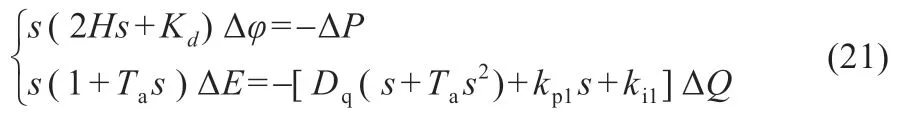
令Y1=( Δφ′,ΔE′,Δφ,ΔE)T，Δφ′為Δφ 對時間的導數，ΔE′為ΔE 對時間的導數，根據式(19)～(21)可得并網模式下基于VSG-MPC 控制的儲能換流器的小信號模型為:

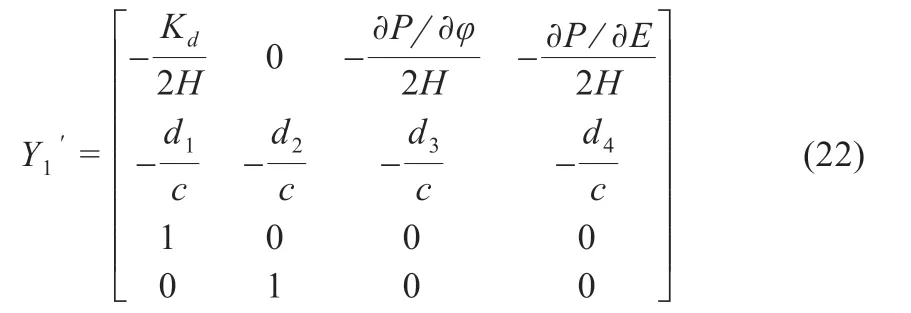
其中：

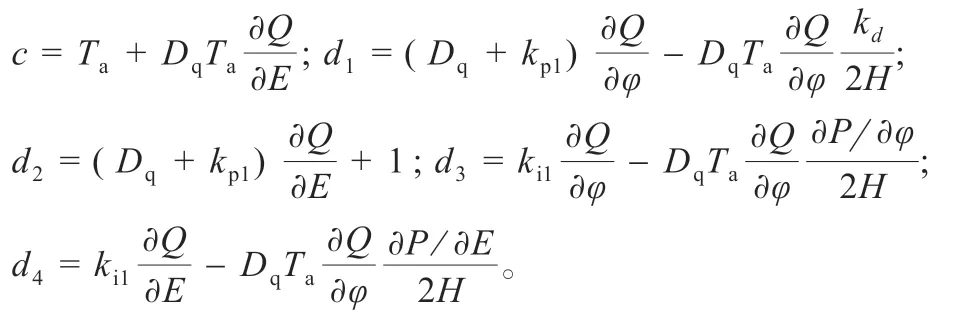
當系統處于并網狀態時，控制參數對系統的穩定性有著較大的影響，因此，需要對式(22)狀態空間方程的特征根進行靈敏度計算。同理，狀態空間方程的特征根對參數K 變化的靈敏度可定義為：

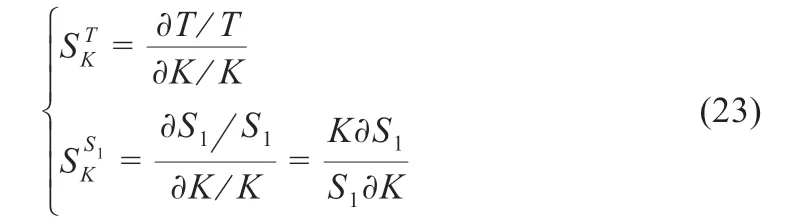
式中：K 為變化的函數；T 為傳遞函數；S1為特征方程的根。

根據式(22)由特征根軌跡可以計算出基于MPC 的VSG控制參數k1變化的靈敏度為40.325+1.235j，參數k2變化的靈敏度為-7.233-2.436 j。因此，選擇慣性時間常數k1=1.2，慣性時間常數k2=0.8 可保證系統的穩定性，且系統工況變化時處于過阻尼狀態。圖11 為離網下PCS 仿真波形。圖12 為并網下PCS 仿真波形。由仿真結果圖12(d)可知，當系統功率指令發生變化時有功功率不會超調，虛擬轉子角不會振蕩。

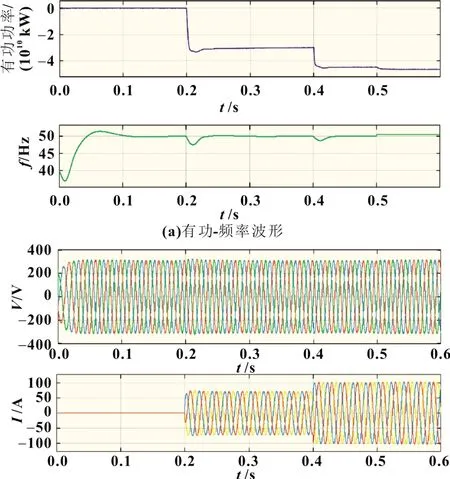
圖11 離網下PCS仿真波形

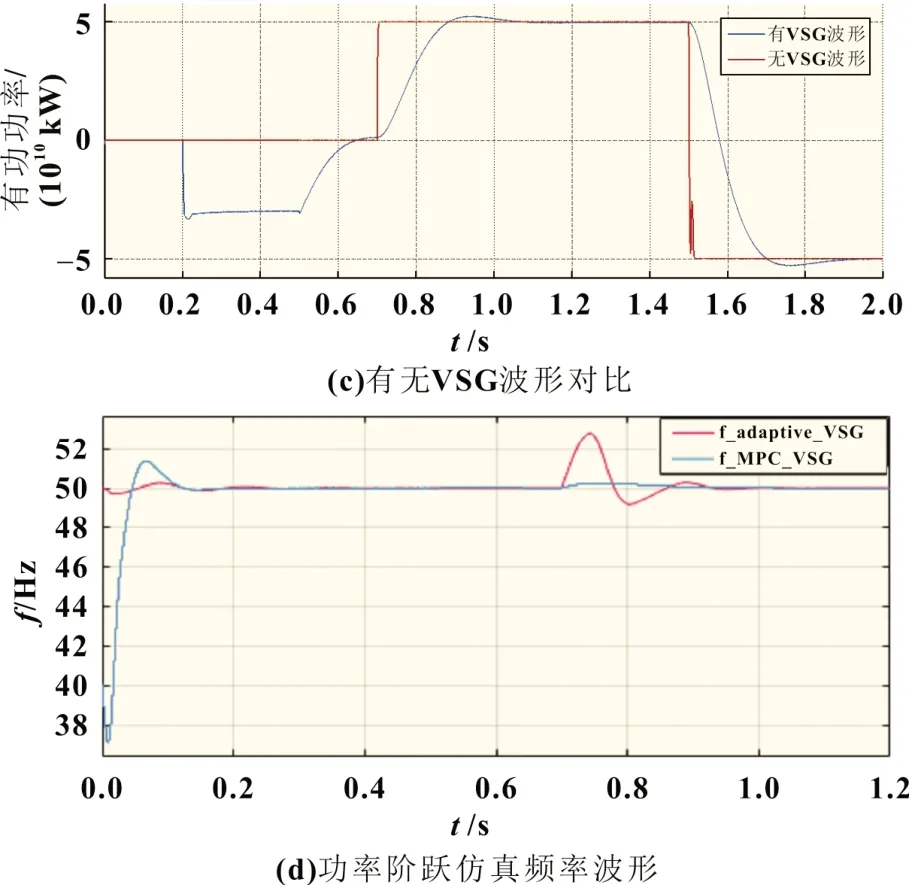
圖12 并網下PCS 仿真波形

結合圖1 驗證所提出的控制策略的有效性，先單獨驗證基于VSG_MPC 的儲能系統在離網運行及并網運行下的有效性：

(1)離網運行

仿真場景：PCC 點處斷開，PCS 脫網運行，仿真時長為0.6 s。t=0.2 s 時，突加負荷P=30 kW，Q=15 kVar；t=0.4 s 時，突加負荷P=15 kW，Q=0 Var(仿真結果見圖11)。

從仿真結果可以看出，當負荷發生持續的投切及波動時，PCS 發出的有功功率能快速響應系統的變化，頻率在較短時間內恢復到了額定頻率50 Hz；電壓電流波形變化平穩，無明顯畸變。

(2)并網運行

仿真場景：VSG 設置了并網預同步功能(見圖5)，利用虛擬功率產生并網預同步的信號。由離網轉并網時，儲能換流器在t=0～0.5 s 時處于離網狀態，t=0.2 s 時突加30 kW 的有功負荷，t=0.5 s 時接入電網，PCS 并網運行，仿真時長為2 s(仿真結果見圖12)。其中，為了驗證本文所提出控制策略中慣量響應對系統穩定性的影響，將基于自適應虛擬慣量的VSG與本文所提出的VSG 控制策略進行對比分析，由仿真波形圖12(d)可對比分析其轉子角的穩定性。

從仿真結果可以看出，t=0.5 s 時PCS 平滑接入電網，無明顯的電壓波形，此時PCS 功率逐漸將為0；t=0.7 s 時，給定有功功率50 kW，PCS 迅速響應指令，且平穩到達給定值；t=1～1.5 s時，電網自身的頻率波動+0.5 Hz。有功響應快速跟隨頻率的變化，當頻率恢復時，PCS 在0.2 s 內跟蹤上給定功率指令，且電壓無明顯波動，電流變化平穩。如圖12(c)加入VSG 的時候，有功響應更加平滑，動態性能更好。由于加入了MPC 控制策略[見圖12(d)]，即使在轉動慣量固定的情況下，相比基于自適應的VSG，當系統發生30 kW 的有功功率階躍時，本文所提出的控制策略能更有效地抑制虛擬轉子角的振蕩，更好地改善系統的頻率及功率的動態響應及穩定性。

6 結論

通過以上分析可知，以VSG_MPC 為基礎的雙向儲能換流器控制系統，其外環采用虛擬同步機(VSG)有功功率控制策略，因其模擬了同步發電機的外特性優勢，所以增加了其自身能力，如阻尼能力、慣性能力等；內環采用直接功率預測MPC 控制策略，克服了采用傳統PI 對參數敏感及變結構控制時魯棒性差的缺點，建模要求低，不需要進行參數設計，自適應和穩定性較高，通過在線優化，可以提高控制的精度，可以有效抑制虛擬轉子角速度的來回振蕩和有功功率調節越限，從而使系統的性能指標得到明顯提高。

致謝：董建園老師在本文研究工作方面提出了指導性意見，謹此深表感謝。