安全高效的兩方協同ECDSA 簽名方案

王婧，吳黎兵,，羅敏，何德彪

（1.武漢大學計算機學院，湖北 武漢 430070；2.武漢大學國家網絡安全學院，湖北 武漢 430070）

1 引言

橢圓曲線數字簽名算法（ECDSA,elliptic curve digital signature algorithm）是橢圓曲線加密（ECC,elliptic curve cryptography）與數字簽名算法（DSA,digital signature algorithm）的結合，于1999 年成為美國國家標準學會（ANSI,America National Standards Institute）標準，并于2000 年成為電氣和電子工程師協會（IEEE,Institute of Electrical and Electronics Engineers）、美國國家標準與技術研究院（NIST,National Institute of Standards and Technology）標準[1]。與DSA 和RSA（Rivest-Shamir-Adleman）相比，ECDSA 具有計算量小、處理速度快、存儲空間占用小、帶寬要求低等特點，適用于計算能力、存儲空間、帶寬與功耗受限的應用場景。因此，ECDSA 被廣泛應用于電子商務系統[2]和其他網絡領域，如安全傳輸層（TLS,transport layer security）協議[3]和域名系統安全擴展（DNSSEC,domain name system security extension）協議[4]，用于提供身份認證、數據完整性驗證、不可否認性等安全服務。隨著比特幣系統的成功部署與應用，ECDSA 受到更廣泛的關注，并逐漸成為當前主流區塊鏈平臺及項目的默認簽名機制，如以太坊和Hyperledger Fabric。

眾所周知，數字簽名方案的安全性依賴于簽名者私鑰的安全性。在區塊鏈系統中，私鑰是用戶掌控其密碼貨幣的關鍵，也是實施隱私保護方案的基礎。用戶發布交易時，需要先使用簽名私鑰對交易進行簽名，只有被共識節點驗證通過的交易才能成功上鏈，實現密碼貨幣的轉移或信息發布。惡意攻擊者一旦非法竊取了區塊鏈用戶的簽名私鑰，就可以任意轉移該用戶的密碼貨幣或冒充該用戶發布非法交易信息。近年來，密碼貨幣被盜事件頻發，造成嚴重的經濟損失[5-6]。與傳統銀行電子交易系統不同，一旦區塊鏈密碼貨幣被轉移，就無法追回。即使用戶已知私鑰被濫用，成功上鏈的交易也無法撤回。2019 年2 月，加拿某平臺誤將102 枚比特幣發送到私鑰僅被已去世的首席執行官所知的冷錢包，導致這些比特幣被永久鎖死[7]。因此，防止私鑰泄露并避免簽名權利過度集中是當前基于簽名技術的網絡交易系統和區塊鏈系統亟待解決的問題。

為了解決這一問題，常見的解決方法有多重簽名、基于Shamir 秘密共享的(t,n)?門限簽名和基于安全兩方/多方計算的簽名。其中，多重簽名通常發生在區塊鏈上，區塊鏈需要引入一種對多重簽名進行編碼的方法，并對區塊鏈進行重塑以完成基于多重簽名交易的發布與驗證，現有區塊鏈難以支持這種技術。此外，不同簽名者在區塊鏈上進行多次簽名，訪問結構（簽名者的身份、數量）容易暴露在區塊鏈上，從而可能導致用戶隱私泄露，且簽名長度隨簽名者數量呈線性增長，簽名驗簽時需要多個公鑰參與驗證，開銷較高[8]。基于Shamir 秘密共享的(t,n)?門限簽名往往需要借助一個可信中心為預先選定的簽名群體分發私鑰份額，并且需要至少t個簽名方重構出完整的私鑰才能完成簽名。在實際情況下，頒發私鑰的中心和簽名時重構的私鑰持有者便成為系統的安全瓶頸[9]。基于安全兩方/多方計算的簽名可在區塊鏈下實施，不需要在鏈上執行所有過程，而且兩方/多方計算簽名中簽名者信息被折疊成常規的區塊鏈交易格式，因而能夠兼容現有區塊鏈系統并降低開銷，并在一定程度上保證用戶隱私。

MacKenzie 等[10]首次提出了針對DSA 的兩方協同簽名方案，可以使2 個簽名參與方對給定的公鑰生成有效的DSA 簽名，而任何一方都不能單獨完成簽名，簽名過程中不需要重構私鑰。Gennaro等[11]針對比特幣錢包安全提出了一種基于門限加法同態加密技術的(t,n)?門限DSA/ECDSA 簽名方案，并在惡意模型下證明了其安全性。Boneh 等[12]對文獻[11]方案進行了性能優化，提出了基于level-1 全同態加密的門限DSA/ECDSA 簽名方案。然而，這些方案均使用了分布式同態加密密鑰生成技術，簽名參與方的通信開銷和計算開銷都非常高，難以實際應用于處理能力受限的比特幣錢包服務或計算能力受限的區塊鏈客戶端。

Lindell[13]提出了基于Paillier 同態加密算法的兩方協同ECDSA 簽名方案，與上述方案不同的是，該方案不需要執行分布式Paillier 密鑰算法，直接利用Paillier 同態屬性即可完成兩方協同簽名，提高了兩方協同簽名的運行效率。為了滿足用戶對安全的差異性需求，Doerner 等[14]提出了基于秘密共享和不經意傳輸技術的(2,n)?門限ECDSA 簽名方案，該方案不需要引入計算開銷較高的Paillier 同態加密及其相關的零知識證明，從而大大提高了協同簽名的計算性能。但是Doerner 方案引入了不經意傳輸協議[15-16]，與Lindell 方案[13]相比，增加了近千倍的通信開銷，且不能應用于帶寬受限的區塊鏈客戶端。Castagnos 等[17]使用哈希證明系統技術代替Lindell 方案[13]中的Paillier 同態加密技術，設計了一種新的兩方協同ECDSA 簽名方案，進而完善了Lindell 方案[13]的安全性證明。然而，對于128 bit安全的ECDSA 簽名方案，Castagnos 方案[17]的運行效率比Lindell 方案[13]更低。

除兩方協同的ECDSA 簽名方案之外，多方門限ECDSA 簽名方案也陸續被提出。Lindell 等[18]設計了一種安全隱私乘法協議，用于將原始的兩方協同簽名方案擴展成多方門限簽名方案。Doerner 等[19]同樣將Lindell[13]原始的兩方門限ECDSA 簽名方案擴展成了多方門限ECDSA 簽名方案。Gennaro 等[20]設計了一種基于Paillier 同態加密的MtA 協議，該協議可以將基于乘法的共享份額轉換為基于加法的共享份額，進而基于該協議提出一種新的多方門限ECDSA 協同簽名方案。但是，這些方案仍然沿用了兩方協同簽名方案中所使用的同態加密算法或不經意傳輸協議，因而計算開銷和通信開銷非常高。

除ECDSA 之外，國內外學者還提出了對其他密碼算法的私鑰保護安全解決方案。針對基于身份的數字簽名，He 等[21]和Feng 等[22]分別提出針對IEEE P1363 標準的兩方協同簽名方案和多方協同簽名方案。侯紅霞等[9]針對我國商用密碼算法SM2，結合Lindell 方案[13]的思想設計了一種兩方協同SM2 簽名方案。Zhang 等[23]同樣基于Paillier 同態加密算法，設計了一種新的兩方協同SM2 簽名方案。Mu 等[24]針對我國商用密碼算法SM9，設計了基于Paillier 的兩方協同SM9 簽名方案。然而，這些方案一方面計算開銷或通信開銷較高，難以適用于計算能力或帶寬受限的客戶端；另一方面，難以兼容現有的區塊鏈系統。

因此，為了提高協同簽名的運行效率、降低簽名過程的通信開銷、保證簽名私鑰安全并兼容當前區塊鏈系統，對兩方/多方協同ECDSA 簽名方案進行進一步研究具有非常重要的理論意義和現實意義。針對這一目標，并考慮到兩方簽名對客戶端的友好性與便捷性，本文設計了一種新的安全高效兩方協同ECDSA 簽名方案。本文的主要貢獻可分為以下3 個方面。

1)設計了一種安全高效的兩方協同ECDSA 簽名方案，通過預計算Beaver 三元組[25]，避免使用計算開銷高昂的Paillier 同態加密和通信開銷高昂的不經意傳輸技術，2 個參與方在不暴露各自私鑰的情況下共同完成簽名。

2)對本文所提方案提供了完整的安全性證明，結果表明，所提方案在不同時腐化2 個簽名方的情況下能夠有效保護ECDSA 簽名私鑰。

3)從理論分析和模擬驗證2 個方面對本文所提方案進行了評估，并與2 個相關的兩方協同簽名進行了比較，結果表明，本文所提方案在計算開銷和通信開銷上都具有明顯優勢。

2 預備知識

2.1 ECDSA 數字簽名算法

系統建立輸入安全參數，輸出算法公開參數param={E,G,P,p,q,h}，其中，E為定義在有限域Fp上的橢圓曲線，p為一個素數，G為橢圓曲線上所有整數點構成的加法群，P和q分別為群G的生成元和素數階，h為輸入映射到域的雜湊函數，即域由整數集合{1,2,…,q?1}構成。

密鑰生成輸入算法公開參數param，輸出簽名私鑰d和驗證公鑰Q，其中d∈為隨機秘密值，公鑰Q=dP可公開發布。

簽名生成輸入算法公開參數param、用戶私鑰d和待簽名消息m，輸出簽名σ=(r,s)。具體步驟如下。

1)選擇一個隨機數k∈，計算R=k?P=(rx,ry)，其中rx和ry分別為橢圓曲線上點R的橫坐標和縱坐標。

2)計算r=rxmodq，若r=0，則返回步驟1)；否則，執行步驟3)。

3)計算s′=k?1(e+dr)modq，其中，e=h(m)為消息摘要。

4)輸出簽名信息σ=(r,s)，其中s=min{s′,q?s′}，min{}函數表示取集合中較小的數值。

簽名驗證輸入待驗證的消息m和簽名σ，輸出驗證結果“1”或“0”。具體步驟如下。

1)解析簽名σ獲得(r,s)，計算摘要e=h(m)。

2)計算Rv=s?1(eP+rQ)=(xv,yv)。

3)若r=xvmodq，輸出1；否則輸出0。

2.2 Beaver 三元組乘法技術

Beaver 三元組乘法技術由Beaver[25]于1991 年首次提出，通過完全隨機地設置電路中每個門的輸入，然后進行校正的方法實現安全多方乘法計算。該方法避免了標準的安全兩方或多方乘法協議中涉及的零知識證明或進一步秘密值共享等操作/協議，只需要進行簡單的消息隨機秘密值廣播和重構即可實現安全兩方或多方乘法計算。為了簡便，本文將在后續描述中省略整數運算涉及的“modq”符號。

假設參與方U1和參與方U2已分別存有各自的秘密共享份額{ai,bi,Δai,Δbi,Δci}，i∈{1,2}，其中Δai和Δbi是完全隨機的整數，整數Δc1和Δc2滿足條件Δc1+Δc2=(Δa1+Δa2)(Δb1+Δb2)，U1和U2的目標為安全計算c=c1+c2=(a1+a2)(b1+b2)。基于Beaver 三元組的安全兩方乘法協議步驟如下。

U1先分別計算其盲化數據u1=a1?Δa1和，再發送(u1,v1)給U2。U2先分別計算其盲化數據u2=a2?Δa2和v2=b2?Δb2，再發送(u2,v2)給U1。

U1進而可計算中間數據u=u1+u2、v=v1+v2和c1=Δc1+Δa1v+Δb1u。U2同理可計算中間數據u=u1+u2、v=v1+v2和c2=Δc2+Δa2v+Δb2u+uv。

最后，U1和U2交換各自的信息c1和c2，從而兩方均可計算結果c=c1+c2=(a1+a2)(b1+b2)。

正確性令c=c1+c2，a=a1+a2，b=b1+b2，Δc=Δc1+Δc2，Δa=Δa1+Δa2，Δb=Δb1+Δb2，則u=a?Δa，v=b?Δb，進一步地，通過以上步驟可得

因此，利用Beaver 三元組可以進行兩方乘法計算。

安全性文獻[25]指出{Δai,Δbi}是隨機選取的，且每組數據僅使用一次，相當于獨立且均勻分布的一次一密隨機值，允許通信方在公開信道上發送具有完全隱私性的任意消息。此外，Beaver 分別證明了該方法在消息被篡改（詳見文獻[25]的安全性證明引理4 和引理6）和參與方被腐化（詳見文獻[25]的引理5 和引理7）情況下的安全性。因此，本文認為該方案在不需要引入承諾與零知識證明等額外密碼原語的情況下，滿足半誠實模型和惡意模型下的安全性。

一次性表Beaver[25]提出了一次性表的概念，用以描述一系列支持安全兩方或多方計算的三元組對集合，如SETtri={(Δa1i,Δb1i,Δc1i),(Δa2i,Δb2i,Δc2i)}，其中i={1,2,…,N}，N表示集合大小。其中U1將獲得大小為N的三元組集合 SETt1ri=，對稱地，U2將獲得大小為N的三元組集合此外，為了提高計算效率與安全性，Beaver 建議通過離線預計算的方式來獲取 SETtri。

安全離線預計算協議Fp re在三元組構造過程中，(Δa1,Δb1)和(Δa2,Δb2)分別由U1和U2隨機選取，然后通過交互計算得到c1和c2，可以觀察到

其中，Δa1Δb1和Δa2Δb2可分別由U1和U2本地計算，因此構建三元組的難點在于如何計算Δa1Δb2和Δa2Δb1。Feng 等[26]基于現有成果列舉了3 種生成Beaver 三元組的安全預計算方法。①首先基于加法同態加密技術構造一個乘法共享轉加法共享的協議，再基于此計算Δa1Δb2和Δa2Δb1。以基于Paillier同態加密的方法為例：U1首先生成Paillier 的公私鑰對(sk,pk)，計算密文x1=Encpk(Δa1)，將x1和公鑰pk 發送給U2；U2收到消息后選取一個隨機數η，計算密文，再將密文x2發送給U1；U1可解密獲得y1=Δa1Δb2?η；類似地，重復上述步驟，U1可獲得y1′=Δa2Δb1?η′，進而可以計算出Δc1=Δa1Δb1+y1+y1′；U2根據計算過程中選取的隨機數可計算Δc2=Δa2Δb2+η+η′。該方法首次在文獻[20]中被應用，并且其安全性也得到了證明。②與第一種方法類似，先計算Δa1Δb2和Δa2Δb1，再計算Δc1和Δc2，不同點在于用不經意傳輸協議代替加法同態加密技術以節約計算開銷，具體實施方案可參考文獻[14]。③基于可信第三方頒發有效的Beaver 三元組，如利用一個可信的服務器為U1和U2生成匹配的三元組，該方法在文獻[27]中被應用。后文為了簡便，令 Fpre表示安全的三元組離線預計算協議。

3 安全模型和設計目標

3.1 安全性定義

本節主要描述數字簽名方案與兩方協同數字簽名方案的安全性定義。

1)標準數字簽名安全性定義

與文獻[13]類似，出于完整性和參考性目的，本文首先針對標準數字簽名方案π=(Gen,Sign,Verify)給出一個基于游戲的安全性定義。游戲GameSignA,π(1λ)中共2 個角色，即概率多項式時間（PPT,probabilistic polynomial time）敵手A 和模擬器C。其中，C 為PPT 敵手A 提供方案相關的公開參數，包括簽名驗證公鑰Q，同時提供對A 的簽名查詢應答；PPT 敵手A 的目標是在進行若干消息?簽名對查詢后，偽造消息m*的簽名σ*；若偽造成功，則游戲輸出“1”，否則游戲輸出“0”。A 和C 的游戲流程如算法1 所示。

算法1標準數字簽名

游戲1GameSignA,π(1λ)

①(d,Q)←Gen(1λ)

② A 將消息m∈{01}*發送給C 進行簽名詢問CSignd(?)，C 返回m的合法簽名σ；/*該步驟執行次數在多項式范圍內，所有查詢過的消息m構成集合Ω*/

③(m*,σ*)←ASignd(?)(1λ,Q)；/*敵手A 進行簽名偽造*/

④ 當且僅當 Verify(m*,σ*)=1 且m*?Ω時，游戲輸出“1”；否則游戲輸出“0”

定義1如果對于任意的PPT 敵手A，在游戲1中輸出“1”的概率是可忽略的，即

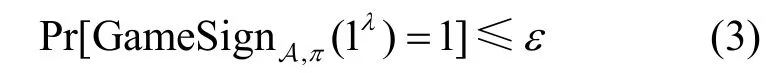
其中，ε為一個可忽略概率閾值，λ為簽名方案π的安全參數，則認為簽名方案π滿足選擇消息攻擊下的存在不可偽造性安全（EU-CMA,existential unforgeability against chosen-message attack）。

2)兩方協同簽名安全性定義

兩方協同簽名可視為標準數字簽名的一種分布式表現形式，其輸出的簽名仍能通過算法Verify的驗證，因此，本文采用類似于簽名方案π的方式定義π衍生的兩方協同簽名方案Π=(DistGen,DistSign,Verify)的安全性。

與標準數字簽名安全定義不同的是，本文假設PPT 敵手A 可以控制其中一個簽名參與方Ui(i∈{1,2})，并且知道Ui的所有秘密值。因此，A和被腐化的Ui被認為是一體的，在后續描述中稱Ui為腐化方或直接用A 代替Ui來描述游戲模擬過程。在模擬過程中，A 選擇要簽名的任意信息，與誠實參與方Uj(j≠i)進行交互生成簽名。同時，A可以選擇遵循協議設置或任意偏離協議設置，即敵手是惡意的。此外，敵手A 是靜態的，即在協議初始化之前，敵手A 便確定被控制的參與方為Ui，且在一個游戲結束之前不會轉換為參與方Uj。

算法2兩方協同數字簽名

游戲2GameDistSignA,Π(1λ)

①Q←Πi(1λ)；/*誠實參與方輸出簽名驗證公鑰，Ui被敵手控制*/

② A 選擇m∈{01}*作為待簽名的消息，與Πi(.)進行交互輸出簽名σ；/*該步驟執行次數在多項式范圍內，所有査詢過的消息m構成集合Ω*/

④ 當且僅當Verify(m*,σ*)=1 且m*?Ω時，游戲輸出“1”；否則游戲輸出“0”

定義2如果對于任意的PPT 敵手A 以及被A 腐化的任意參與方Ui(i∈{1,2})，在游戲2 中輸出“1”的概率是可忽略的，即

其中，ε為一個可忽略概率閾值，則認為簽名方案Π滿足選擇消息攻擊下的存在不可偽造性安全。

3.2 安全模型

通用可組合（UC,universally composable）安全是由Canetti[28]提出的一種根據協議現實執行環境和協議理想執行環境不可區分方法來定義密碼協議安全性的框架。該框架的顯著特點是：當一個組合協議的各個子協議被證明是UC 安全的，那么該組合協議是安全的。因此，可以模塊化地選取或設計可證明安全的子協議，進而運用組合原理構造更復雜的安全密碼協議。

在UC 框架下，理想函數F 是重要的組成部分，代表一個不可腐化的可信方，用于完成協議所需的理想功能與執行過程。PPT 敵手A 與協議參與方的交互用于模擬協議的現實執行過程，即協議現實執行環境。協議參與方（包括可視為理想敵手的模擬器C ）與理想函數的交互用于模擬協議的理想執行過程，即協議理想執行環境。本文提出的兩方協同ECDSA簽名方案是基于理想函數和組合的混合模型構造的。同時，本文方案的安全性也是基于此模型進行證明的。其中，分布式密鑰生成模擬只需執行一次，兩方協同簽名模擬可執行多項式次數。值得注意的是，如果承諾與零知識證明協議是UC 安全的，那么在混合模型下協議模擬執行的輸出和協議現實執行的輸出在計算上是不可區分的。接下來，本文將對這幾個理想函數進行簡單介紹。

1)承諾理想函數 Fcom

在隨機預言機模型下，Fcom可通過簡單地定義函數Com(x)=h(x,r)←{0,1}λ來實現靜態安全，且任意滿足通用可組合安全的承諾函數h都滿足 Fcom的形式化定義[13]，具體流程如下。

①當收到參與方Ui的消息(commit,sid,x)后，如果已經存儲會話序號 sid 相關的承諾消息(commit,sid,?)，則忽略此消息；否則，記錄消息(sid,i,x)，并且將(receipt,sid)發送給參與方Uj。

② 當收到參與方Ui的消息(decommit,sid)后，如果已經存儲消息(sid,i,x)，則將消息(decommit,sid,x)發送給參與方Uj。

根據文獻[13,18]可知，標準零知識理想函數可形式化定義為

其中，str 表示空字符串，R 表示秘密信息x和證據ω之間的關系。在安全兩方計算場景下，非交互式零知識證明理想函數與2 個參與方Ui、Uj的形式化交互流程如下。

當收到參與方Ui的消息(prove,sid,x,ω)后，如果會話序號sid 已被使用過或秘密信息x和證據ω之間不滿足關系R，即(x,ω)?R，則忽略本次的消息；否則，將(proof,sid,x)發送給參與方Uj。

①當收到參與方Ui的消息(com-prove,sid,x,ω)后，如果會話序號 sid 已被使用過或(x,ω)?R，則忽略本次的消息；否則，將(proofreceive,sid)發送給參與方Uj。

② 當收到參與方Ui的消息(decom-proof,sid)后，如果已存儲了(sid,i,x)，則將(decom-proof,sid,x)發送給參與方Uj。

在本文的方案設計中，R 為橢圓曲線上的離散對數關系，定義為RDL={(G,P,q,Q,x)|Q=xP}。對于關系RDL的零知識證明，本文可以采用經典的Schnorr 證明[29]來實現。

3.3 設計目標

本文提出的兩方協同ECDSA 簽名方案應滿足以下4 個屬性。

①隱私性。除協議的計算輸出和協議本身所泄露的內容外，2 個簽名參與方中的任何一方都不能從協議執行過程中獲取其他任何信息，包括另一方的私有輸入。

② 正確性。2 個簽名參與方誠實地執行該協議時，協議輸出合法的ECDSA 簽名。

③兼容性。協議輸出的正確簽名仍能通過原簽名方案驗證算法的檢測，即使用2.1 節描述的簽名驗證算法時，簽名驗證結果為“1”。

④ 高效性。充分考慮參與方的計算能力以及協同簽名過程中的在線時延，簽名過程應保證計算開銷和通信開銷盡可能小。

4 方案設計

本文提出的兩方協同ECDSA 簽名方案共包括4 個階段，分別為系統建立、分布式密鑰生成、兩方協同簽名和簽名驗證。系統建立和簽名驗證與2.1節中的描述一致，因此本節不再重復描述。分布式密鑰生成和兩方協同簽名協議由2 個簽名參與方U1和U2協同完成，其中分布式密鑰生成算法只需運行一次，兩方協同簽名算法可運行多次。

在本文方案中，假設在運行分布式密鑰生成和協同簽名協議之前，系統已執行過（如第2.2 節所描述的）安全離線預計算協議 Fpre，并安全輸出了簽名參與方U1和U2所需的Beaver 三元組集合。換句話說，U1和U2在簽名之前已秘密保存了配對的三元組集合，從而降低了在線協同簽名的通信開銷與計算開銷。Beaver 三元組的離線預計算理念已在多個方案中被應用，如文獻[26-27,30]。根據文獻[25]的定義，為了保證協議在UC 框架下的安全性，Beaver 三元組應為一次一密隨機值。因此，本文可根據實際應用場景需求，選擇定期執行安全預計算協議來更新集合，以獲得足夠使用的三元組數量，或者一次性預計算出足夠多的三元組。下面，將具體介紹本文提出的兩方協同ECDSA 簽名方案的分布式密鑰生成協議與兩方協同簽名協議。

4.1 分布式密鑰生成

分布式密鑰生成協議由簽名參與方U1和U2共同完成，輸出簽名驗證公鑰Q和各自的部分私鑰d1,d2。

1)U1→U2:{com(Q1,π1)}

①U1選取一個隨機數d1∈Zq*作為U1的部分私鑰，計算對應的部分公鑰Q1=d1P。

②U1發送消息(com-prove,1,Q1,d1)給理想函數（即U1發送關于Q1及其離散對數的零知識證明π1的承諾com 給U2）。

2)U2→U1:{Q2,π2}

①當U2接收到的消息(proof-receipt,1)后，U2選取一個隨機數作為U2的部分私鑰，計算對應的部分公鑰Q2=d2P。

②U2發送消息(prove,2,Q2,d2)給理想函數（即U2發送Q2和關于Q2的離散對數零知識證明π2給U1）。

3)U1→U2:{Q1,π1}

當U1接收到的消息(proof,2,Q2)后，U1驗證proof 的有效性，若無效則協議終止；否則，打開承諾并發送消息(decom-proof,1)給（即U1發送Q1和關于Q1的離散對數零知識證明π1給U2）。

4)U1和U2輸出簽名驗證公鑰Q，并安全存儲各自的隱私信息

①U1計算簽名驗證公鑰，并安全存儲

② 當U2接收到理想函數的消息(decom-proof,1,Q1)后，U2驗證proof 的有效性，若無效則協議終止；否則，計算簽名驗證公鑰Q=Q1+Q2，并安全存儲

4.2 兩方協同簽名

給定待簽名的消息m，兩方協同簽名協議必須由參與方U1和U2共同完成，輸出ECDSA 簽名σ=(r,s)。

1)U1→U2:{com(R1,π3)}

①U1選取一個隨機數，計算R1=k1P。

②U1發送消息(com-prove,sid||1,R1,k1)給理想函數（即U1發送關于R1及其離散對數的零知識證明π3的承諾com 給U2）。

2)U2→U1:{R2,π4}

①當U2接 收 到的 消 息(proof-receipt,sid||1)后，U2選取一個隨機數，計算R2=k2P。

②U2發送消息(prove,sid||2,R2,k2)給理想函數（即U2發送R2和關于R2的離散對數零知識證明π4給U1）。

3)U1→U2:{R1,π3,(u1,v1,w1,t1)}

①當U1接收到的消息(proof,sid||2,R2)后，U1驗證proof 的有效性，若無效則協議終止；否則，打開承諾并發送消息(decom-proof,sid||1)給（即U1發送R1和關于R1的離散對數零知識證明π3給U2）。②U1依次計算R=R1+R2=(rx,ry)、r=rxmodq、，其中，e=h(m)，如果e為奇數，U1進一步計算，令δ1=δ1+1。

③U1先選擇一個隨機數，再按順序選擇中前2 個三元組(Δa11,Δb11,Δc11)和(Δa12,Δb12,Δc12)，進而分別計算數據u1=k1?Δa11、v1=ρ1?Δb11、w1=δ1?Δa12和t1=ρ1?Δb12。

④U1發送消息{u1,v1,w1,t1}給U2。

4)U2→U1:{(u2,v2,w2,t2),(α2,β2)}

①當U2接收到理想函數的消息(decom-proof,sid||1,R1)后，U2驗證proof 的有效性，若無效則協議終止；否則，依次計算R=R1+R2=(rx,ry)、r=rxmodq和消息雜湊值e=h(m)，并且計算

② 當U2接收到U1的消息(u1,v1,w1,t1)后，U2先選擇一個隨機數，再按順序選擇中前2 個三元組(Δa21,Δb21,Δc21)和(Δa22,Δb22,Δc22)，進而分別計算數據u2=k2?Δa21、v2=ρ2?Δb21、w2=δ2?Δa22和t2=ρ2?Δb22。

③U2先分別計算數據u=u1+u2、v=v1+v2、w=w1+w2、t=t1+t2，接著計算數據α2=k2v+ρ2u+Δc21、β2=δ2t+ρ2w+Δc22。

④U2刪除當前中的三元組(Δa21,Δb21,Δc21)和(Δa22,Δb22,Δc22)，然后將消息{(u2,v2,w2,t2),(α2,β2)}發送給U1。

5)U1輸出簽名σ=(r,s)

①當U1收到U2的消息{(u2,v2,w2,t2),(α2,β2)}后，U1先計算u=u1+u2、v=v1+v2、w=w1+w2、t=t1+t2、α1=k1v+ρ1u+Δc11?uv和β1=δ1t+ρ1w+Δc12?tw，然后刪除SETt1ri中的三元組(Δa11,Δb11,Δc11)和(Δa12,Δb12,Δc12)。

②U2計 算，令s=min{s′,q?s′}，輸出ECDSA 簽名σ=(r,s)

若應用場景需要U2也輸出簽名，U1可將消息(α1,β1)給U2，則U2也可按照步驟5)計算獲得簽名σ=(r,s)。由于在Beaver 三元組乘法技術中，三元組必須遵循一次一密的原則才能滿足多方計算的完美隱私性，因此U1和U2在每次簽名之后刪除已使用的三元組，避免簽名過程中重復使用三元組。此外，當應用場景安全要求較低時，可刪除方案涉及的所有承諾協議和零知識證明協議，即構成半誠實模型[31]下的安全兩方協同ECDSA 簽名方案，從而進一步提高協同簽名的效率。

4.3 正確性分析

根據分布式密鑰生成算法可得，簽名驗證公鑰為

根據兩方協同簽名算法可得

此外，同理于2.2 節中Beaver 三元組乘法技術的正確性分析，即式(1)，可得

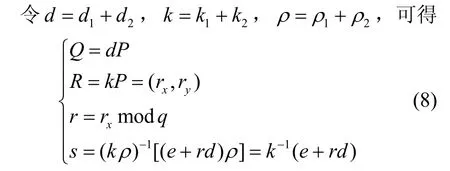
由此可知，本文所提兩方協同ECDSA 簽名方案輸出的簽名(r,s)和簽名驗證公鑰Q與2.1 節描述的ECDSA 公鑰簽名(r,s)和驗簽公鑰Q一致。因此，本文所提方案滿足設計目標要求的正確性和兼容性。

5 安全性證明

引理1假設ECDSA 簽名方案滿足EU-CMA安全性，那么本文所提兩方協同ECDSA 簽名方案滿足EU-CMA 安全性。

證明假設任意PPT 敵手A 在腐化任意一個協同簽名參與方Ui(i∈{1,2})的情況下，能夠以不可忽略的概率ε 在游戲中成功偽造消息?簽名對(m*,σ*=(r*,s*))，那么本文可以構造一個模擬器C 作為游戲GameSignC,π(1λ)的概率多項式敵手，使C 能夠以與ε 幾乎相等的概率在GameSignC,π(1λ)中成功偽造消息?簽名對(m*,σ*=(r*,s*))。同理于文獻[13]，本文將考慮敵手腐化U1和敵手腐化U2這2 種情況，分別論述本文方案的安全性。其中，分布式密鑰生成協議僅需模擬一次，兩方協同簽名協議可進行多次模擬。假設U1和U2在分布式密鑰生成前已通過安全方式獲得對應的由于Beaver 三元組已被證明是安全的且滿足完美隱私性[25]，因此，為了滿足UC 框架的安全模擬規則（即參與方之間、參與方與敵手間不直接交互），本文在模擬過程中引入一個Beaver 三元組乘法理想函數 FBT，用于接收/發送與Beaver 三元組直接相關的消息。

當i=1時，PPT 敵手A 腐化參與方U1。本文構造一個針對游戲的模擬器C，同時作為游戲GameSignC,π(1λ)的PPT 敵手。本質上，C 在協議模擬過程產生一個令A 不可區分的執行環境，然后利用A 在游戲中輸出的偽造簽名作為游戲GameSignC,π(1λ)的輸出，以此攻擊原始ECDSA 簽名方案。

1)分布式密鑰生成協議模擬

2)兩方協同簽名協議模擬

①在游戲GameSignC,π(1λ)中，C 向預言機FECDSA進行簽名查詢，獲得σ=(r,s)，并根據簽名驗證算法進一步計算得到R。

不可區分性分析。在分布式密鑰生成模擬過程中，可以觀察到協同簽名協議的現實執行環境與理想模擬執行環境僅有一個區別。在協議現實執行環境中，Q2是由誠實參與方U2選擇一個隨機數后計算Q2=d2P得來的；在協議模擬執行環境中，C 計算Q2=Q?Q1=Q?d1P，其中公鑰Q是在游戲GameSignC,π(1λ)中查詢預言機獲取的。由于Q是隨機選取的，因此d2P和Q?d1P是同分布的。此外，若U2不退出協議模擬，敵手A 可在該協議模擬結束后輸出公鑰Q=Q1+Q2=Q1+(Q?Q1)，與在協議現實執行環境中的輸出相同；現實執行環境中的零知識證明與驗證也同分布于()?混合模型。因此，在分布式密鑰生成協議模擬過程中，A對模擬執行環境的視圖和對現實執行環境中的視圖是不可區分的。

在兩方協同簽名模擬過程中，可以觀察到協議現實執行環境與理想模擬執行環境主要有2 個區別。一是計算R2的過程，同理于上述分析，對于A來說，模擬執行過程中的R2=R?k1P和現實執行過程中的R2=k2P是同分布且不可區分的。二是(u2,v2,w2,t2,α2,β2)的構造，在協議模擬環境中，u2,v2,w2,t2,α2均是C 選取的隨機數，而β2是通過計算式β2=s(α1+α2)?β1獲得的；在現實執行環境中，(u2,v2,w2,t2,α2,β2)是通過計算u2=k2?Δa21、v2=ρ2?Δb21、w2=δ2?Δa22、t2=ρ2?Δb22、α2=k2v+ρ2u+Δc21、β2=δ2t+ρ2w+Δc22獲得的。由于ρ2、Δa21、Δb21、Δa22、Δb22均為獨立分布的隨機數，故C 隨機選取的(u2,v2,w2,t2,α2)分別與現實執行環境中誠實參與方U2計算的(k2?Δa21，ρ2?Δb21，δ2?Δa22，ρ2?Δb22，k2v+ρ2u+Δc21)同分布；又因為α2和ρ2是隨機的，所以s(α1+α2)?β1與β2也是同分布的。此外，在模擬協議不終止的情況下，A 可在游戲中輸出當前模擬實例的簽名r=rxmodq和s=(α1+α2)?1?[β1+(s(α1+α2)?β1)]，這與協議現實執行環境中的輸出相同。因此，在U1被腐化時的兩方協同簽名協議模擬的過程中，A 對模擬執行環境的視圖和對現實執行環境的視圖是不可區分的。

簽名偽造。通過上述分析可知，在分布式密鑰生成模擬和兩方協同簽名模擬過程中，A 在腐化參與方U1時無法區分協議現實執行環境和協議模擬執行環境，故C 可以調用A 的偽造簽名攻擊原始ECDSA 方案。

由于在模擬過程中，A 生成的簽名驗證公鑰Q是通過游戲GameSignC,π(1λ)中預言機 FECDSA獲得的，故A 在游戲中的成功偽造(m*,σ*)也可作為C 在游戲GameSignC,π(1λ)中的成功偽造，即A 在游戲輸出一個偽造的消息簽名對(m*,σ*=(r*,s*))，C 可隨之在游戲GameSignC,π(1λ)中輸出(m*,σ*=(r*,s*))。

當i=2時，PPT 敵手A 腐化參與方U2。類似地，本文構造一個針對游戲GameSignC,π(1λ)的PPT敵手C，同時作為游戲的模擬器，能夠利用A 的偽造簽名攻擊原始ECDSA 簽名方案。

1)分布式密鑰生成協議模擬

①在游戲GameSignC,π(1λ)中，C 向預言機FECDSA進行密鑰生成查詢，獲得(1λ,Q)。其中，λ為安全參數，Q為ECDSA 的簽名驗證公鑰。

2)兩方協同簽名協議模擬

①在游戲GameSignC,π(1λ)中，C 向預言機FECDSA進行簽名查詢，獲得σ=(r,s)，并根據簽名驗證算法進一步計算得到R。

④ 當收到 A 發送給FBT的消息(sid,(u2,v2,w2,t2,α2,β2))后，C 驗證A 的消息是否按照4.1 節中步驟4)計算所得，若不是，則終止協議，否則C 輸出σ=(r,s)。

不可區分性分析。在U2被腐化時的分布式密鑰生成模擬過程中，A 對模擬執行環境的視圖和對現實執行環境中的視圖是不可區分的，其原理與U1被腐化時相同，所以本文不再重復描述。

對于U2被腐化時的兩方協同簽名模擬過程，可以觀察到協議現實執行環境與理想模擬執行環境同樣有2 個區別。一是計算R2的過程，同理于上述分析，對于A 來說，模擬執行過程中的R1=R?k2P和現實執行過程中的R1=k1P是同分布且不可區分的。二是(u1,v1,w1,t1)的構造，在協議理想模擬環境中，u1,v1,w1,t1均為C 選取的隨機數；在現實執行環境中，(u1,v1,w1,t1)則通過計算u1=k1?Δa11、v1=ρ1?Δb11、w1=δ1?Δa12、t1=ρ1?Δb12獲得。由于ρ1、Δa11、Δb11和Δa12、Δb12均為獨立分布的隨機數，故C 隨機選取的(u1,v1,w1,t1)分別與現實執行環境中誠實參與方U2計算的(k1?Δa11，ρ1?Δb11，δ1?Δa12，ρ1?Δb12)同分布。此外，在模擬協議不終止的情況下，C 可在游戲中輸出簽名σ=(r,s)。由于σ=(r,s)是向預言機 FECDSA進行查詢而獲得的，故與協議現實執行環境中的輸出相同。因此，在U2被腐化的兩方協同簽名協議模擬過程中，A 對模擬執行環境的視圖和對現實執行環境中的視圖是不可區分的。

簽名偽造。類似地，A 在腐化參與方U2時無法區分協議現實執行環境和協議理想執行環境，C 可以調用A 的偽造簽名攻擊原始ECDSA 方案。由于模擬過程中A 生成的簽名驗證公鑰Q是通過游戲GameSignC,π(1λ)中預言機 FECDSA獲得的，故A 在游戲中的成功偽造(m*,σ*)也為C 在游戲GameSignC,π(1λ)中的成功偽造。因此，若敵手A 能夠以概率ε 贏得游戲那么C 同樣能夠以概率ε 贏得游戲GameSignC,π(1λ)。而原始ECDSA 簽名方案被證明是安全的（滿足定義1）[1]，即概率ε 被認為是可忽略不計的，從而推導出A 贏得游戲的概率可忽略不計（即滿足定義2）。因此，本文提出兩方協同ECDSA 簽名方案在腐化U2時是安全的。

證畢。

綜上所述，本文所提兩方協同ECDSA 簽名方案是可證明安全的。換句話說，在僅一個簽名參與方私鑰泄露的情況下，攻擊者無法完成簽名，這保證了另一簽名參與方的私鑰隱私性，即滿足設計目標的隱私性要求。

6 性能分析

本節將從理論分析與實驗仿真2 個方面對本文所提方案（以下簡稱本文方案）進行性能評估，并與Lindell 方案[13]、Doerner 方案[14]進行比較。由于本文方案和Lindell 方案[13]均為兩方協同ECDSA 簽名方案，故在與Doerner 方案[14]比較時，僅考慮門限為(2,2)時的性能。

6.1 理論分析

首先，通過統計協議執行過程中使用的密碼運算操作個數和網絡傳輸的元素個數，對Lindell方案[13]、Doerner 方案[14]和本文方案的計算開銷和通信開銷進行了理論分析與比較。由于分布式密鑰生成協議只需在系統中執行一次，因此本文主要分析與比較兩方協同簽名協議的計算開銷和通信開銷。

與Paillier 加密、Paillier 解密、Paillier 同態乘、橢圓曲線點乘操作的時間相比，橢圓曲線點加操作的時間可忽略不計，且在方案中使用次數較少，因此對該操作不予統計。令Enc、Dec、HM 分別表示Paillier 算法的加密、解密、同態乘法操作，PM 和h 分別表示橢圓曲線點乘操作和一般哈希操作，N和λ分別表示Paillier 公鑰長度和域上元素長度。此外，為了不失一般性，令輸出簽名的一方為U1，另一方為U2。

由于不同應用環境對方案的安全需求不同，因此，本文分別考慮了方案在半誠實模型下和惡意模型下的計算開銷和通信開銷。半誠實模型下，敵手企圖獲取額外的秘密信息，但在執行過程中不會偏移協議的設置。從方案設計角度，在半誠實模型下，本文方案與Lindell 方案[13]中的參與方不需要執行關于離散對數的零知識證明協議，Doerner 方案[14]中的參與方不需要執行一致性檢測協議。

表1 和表2 分別為惡意模型下和半誠實模型下的計算開銷與通信開銷統計結果。其中，Doerner 方案[14]中哈希操作h 的總個數是在安全參數為256 的情況下進行統計計算的。安全級別越高，Doerner 方案[14]中哈希操作的總數越高，這對計算開銷有一定影響；同時Lindell 方案[13]中的Paillier 加密操作和解密操作的計算效率也會降低。

從表1 可知，在計算開銷方面，與Lindell 方案[13]比較，本文方案在U1端少一個橢圓曲線點乘操作和一個Paillier 解密操作，在U2端少一個Paillier 加密操作、一個同態乘法操作和一個橢圓曲線點乘操作；與Doerner 方案[14]比較，本文方案在U1端和U2端分別少一個和2 個點乘操作，以及數千個哈希操作。因此，在惡意敵手模型下，本文方案的計算開銷最低。

在通信開銷方面，顯然Doerner 方案[14]是最高的；按照NIST 的密鑰長度建議[32]，對于同一安全級別的協議，基于大整數分解的協議密鑰長度約為橢圓曲線密鑰長度的8 倍以上，即N＞8λ，從而可得本文方案的通信開銷比Lindell 方案[13]低。因此，本文方案的通信開銷也是最低的。

從表2 可知，去掉零知識證明協議或一致性檢測協議后，即在半誠實模型下，本文方案由于沒有開銷較高的Paillier 加解密操作和大量的哈希操作，因此在用戶U1端和U2端的計算開銷和通信開銷仍然比其他2 種方案低。

表1 惡意模型下兩方簽名協議計算開銷與通信開銷理論比較

表2 半誠實模型下兩方簽名協議計算開銷與通信開銷理論比較

6.2 實驗仿真

在仿真測試中，本文以 NIST 標準化的secp256k1 橢圓曲線為基準，即安全參數λ=256，雜湊函數則采用SHA-256，Paillier 算法的密鑰長度N=2 048。測試程序基于開源密碼學庫RELIC[33]，并使用C 語言編寫。測試環境為一臺配置為64 位Windows10 專業版操作系統、Intel(R)Core(TM)i5-6300U CPU @ 2.40 GHz 處理器、16.0 GB 內存的惠普筆記本電腦。

在不考慮網絡時延的情況下，本文在局域網內分別對3 種方案的兩方協同簽名協議運行10 000 次，以平均運行時間和通信帶寬為實驗數據。圖1 和圖2 分別為各方案在惡意模型和半誠實模型下的運行時間。

圖1 惡意模型下兩方協同簽名方案的運行時間比較

圖2 半誠實模型下兩方協同簽名方案運行時間比較

從圖1 和圖2 可知，與Lindell 方案[13]和Doerner方案[14]相比，本文方案在兩方協同簽名計算開銷上具有顯著優勢。其中，在惡意模型下，本文方案的簽名運行效率比Lindell 方案快97.42%，比Lindell方案快76.84%。值得注意的是，由于Doerner 方案簽名過程需要參與方進行多次交互，因此，若充分考慮網絡時延，Doerner 方案的實際運行效率將比當前測試結果更低。

表3 為惡意模型和半誠實模型下的通信開銷統計結果。由表3 可知，與Lindell 方案和Doerner 方案相比，本文方案的通信開銷最小。其中，在惡意模型下，本文方案的通信開銷比Lindell 方案小21.74%，比Doerner 方案小99.3%。

表3 惡意模型和半誠實模型下的通信開銷比較

綜上所述，本文所提兩方協同ECDSA 方案在計算開銷和通信開銷上均具有明顯的優勢，滿足設計目標中的高效性要求。

7 結束語

由于簽名私鑰丟失和簽名權利集中都可能損害區塊鏈系統合法用戶的權益，分布式安全計算ECDSA 簽名的研究應運而生。然而現有的兩方或多方協同ECDSA 簽名算法存在計算開銷或通信開銷過高的問題，導致難以廣泛應用于資源受限的用戶端。為了降低簽名私鑰泄露風險并同時保證協同簽名效率，本文提出一種安全高效的ECDSA 兩方協同簽名方案，主要通過引入Beaver三元組預計算技術，避免在協同簽名過程中使用計算繁重的同態加密和通信開銷較大的不經意傳輸等操作，從而實現對簽名私鑰的隱私保護并極大地提高協同簽名的效率。方案的安全性在通用可組合框架下被證明，仿真實驗結果表明，本文方案在簽名計算開銷和通信開銷方面優于現有的兩方協同ECDSA 簽名算法。因此，本文的算法是可行且高效的。