基于CAZAC 序列的低復雜度抗頻偏同步算法

宮豐奎，文妮，李果，高洋

（西安電子科技大學ISN 國家重點實驗室，陜西 西安 710071）

1 引言

正交頻分復用（OFDM,orthogonal frequency division multiplexing）作為一種多載波調(diào)制方式，具有頻譜效率高、抗頻率選擇性衰落和易調(diào)制解調(diào)等優(yōu)點，已被廣泛應用于多個無線通信標準與無線通信場景中，例如最新的 LTE-A（long term evolution-advanced）[1]、5GNR（5th-generation new radio）[2]、DVB-T2（the second generation of digital video broadcasting-terrestrial）[3]、無線局域網(wǎng)（WLAN,wireless local area network）標準[4]等。但是，OFDM 信號也存在一些劣勢，例如其對由多普勒頻移或振蕩器的不穩(wěn)定性所引起的頻率偏移（簡稱頻偏）非常敏感[5]，一旦產(chǎn)生同步誤差，就會破壞子載波間的正交性，從而引入子載波間干擾（ICI,intercarrier interference）和符號間干擾（ISI,intersymbol interference），使OFDM 信號解調(diào)性能急劇降低。因此，OFDM 突發(fā)傳輸系統(tǒng)對同步的要求很高，近年來研究者提出了很多同步算法[6-15]，用來聯(lián)合或單獨估計定時偏差和頻偏。

在OFDM 系統(tǒng)中，按是否需要數(shù)據(jù)輔助，其同步方法可大致分為兩類：非數(shù)據(jù)輔助的盲估計算法和數(shù)據(jù)輔助的估計算法。其中，非數(shù)據(jù)輔助的盲估計算法一般用于連續(xù)傳輸系統(tǒng)中，如DVB-T2，主要是利用OFDM 系統(tǒng)自身的結(jié)構(gòu)特性進行同步，其代表算法是基于循環(huán)前綴的最大似然（ML,maximum likelihood）估計算法[6]，這種算法不需要額外設計同步序列，節(jié)省了系統(tǒng)帶寬，提高了帶寬利用率，但同步性能比數(shù)據(jù)輔助的估計算法差。數(shù)據(jù)輔助的估計算法一般用于突發(fā)通信系統(tǒng)中，主要是利用已知的前導序列，通過捕獲定時度量函數(shù)的峰值完成定時同步，進而完成頻率同步。前導序列主要是由偽噪聲（PN,pseudo-noise）序列或恒包絡零自相關（CAZAC,constant amplitude zero auto correlation）序列等一些自相關、互相關性能良好的序列構(gòu)成。基于PN 序列進行同步的代表性算法有SC算法[7]、Minn 算法[8]、Park 算法[9]和Yang 算法[10]。SC 算法是利用2 個相同的序列進行定時同步的，由于循環(huán)前綴的存在，其定時度量函數(shù)曲線存在平頂效應；Minn 算法在SC 算法的基礎上進行了改進，利用四段特征序列進行定時同步，雖然消除了平頂效應，但存在較高旁瓣；Park 算法設計了一種具有共軛對稱性質(zhì)的訓練序列結(jié)構(gòu)，與SC 算法、Minn算法相比，該算法在正確起始點位置存在一個較大的峰值，提高了定時度量的準確性，但仍存在較小的旁瓣；Yang 等[10]提出了一種基于最優(yōu)相關的循環(huán)移位前導序列的粗符號定時方案，該算法在多徑衰落信道下具有良好的性能，但其旁瓣較高且計算復雜度高。這些算法出現(xiàn)的峰值平頂效應或存在的較大旁瓣對定時同步有一定的影響，而CAZAC 序列良好的相關特性正好可以解決這些問題，因此CAZAC 序列在OFDM 系統(tǒng)的同步中得到了廣泛應用。

基于CAZAC 序列進行同步的代表性算法有Fang 算法[11]、Shao 算法[12]和Jian 算法[13]。Fang 算法是利用隨機指數(shù)序列對CAZAC 序列進行加權(quán)處理來完成定時同步的。Shao 算法則采用一種類似Park 算法的訓練序列結(jié)構(gòu)，在接收端利用新的加權(quán)因子進行定時同步。Fang 算法、Shao 算法在多徑衰落信道下性能良好，但是在接收端進行同步時需要使用額外的加權(quán)序列，這會浪費一些存儲空間，還會增加其計算復雜度。文獻[13]設計了一種新的訓練序列結(jié)構(gòu)，在進行定時同步時可降低計算復雜度，但當存在頻偏時，該算法的定時同步性能明顯下降。Zhang 等[14]提出了一種簡化的互相關檢測器來計算接收樣本與本地序列的相關值，雖然實現(xiàn)復雜度低，但和Jian 算法一樣對頻偏敏感。文獻[15]提出了由Zadoff-Chu 序列及其修正序列級聯(lián)構(gòu)造主前導信號，由2 個不同的循環(huán)移位m 序列構(gòu)造次前導信號的同步方法。

為了解決Jian 算法等典型同步算法對頻偏敏感的問題，同時保證其低實現(xiàn)復雜度，本文設計了一種基于CAZAC 序列的、具有共軛對稱和共軛反對稱結(jié)構(gòu)的新型前導序列，推導了新的對應定時度量函數(shù)及頻偏估計函數(shù)，提出了相應的定時同步及頻率同步方法，并和典型同步算法進行了詳細對比，證明所提算法在同步性能和計算復雜度方面的優(yōu)勢。

2 系統(tǒng)模型

本文考慮突發(fā)復基帶 OFDM 信號幀x(n),n=0,1,2,…,NF?1，NF為突發(fā)幀長，由一段前導序列及數(shù)據(jù)構(gòu)成。OFDM 突發(fā)幀結(jié)構(gòu)如圖1 所示。

圖1 中，NCP為循環(huán)前綴（CP,cyclic prefix）的長度。第m個發(fā)送符號可表示為（不含CP）

其中，dm,k為第m個OFDM 符號中第k個子載波上的調(diào)制符號，m=0,1,2,…,M，當m=0 時xm(n)為前導序列；M為突發(fā)幀中的數(shù)據(jù)OFDM 符號個數(shù)；N為快速傅里葉逆變換（IFFT,inverse fast Fourier transform）點數(shù)；n=0,1,2,…,N?1；j 為虛數(shù)單位。

圖1 OFDM 突發(fā)幀結(jié)構(gòu)

經(jīng)過信道后，假設不存在采樣時鐘頻率誤差，接收到的OFDM 符號可表示為

其中，L為多徑數(shù)目；hl和τl分別為第l徑的復信道衰減和時延；d為時間偏移估計值；ε為相對于子載波間隔fs的歸一化頻偏，，f△為頻偏；w(n)為零均值復高斯白噪聲，n=0,1,2,…,NR?1，NR為接收信號長度。

3 算法描述

3.1 基于CAZAC 序列的新型前導序列設計

本節(jié)設計一種新型前導序列，用于后續(xù)定時同步和頻率同步。如圖1 所示，設計的前導序列由四部分組成，即x0(n)=[xp1(n)xp2(n)xp3(n)xp4(n)]。進一步地，定義CAZAC 序列xp1(n)為

序列xp2(n)是序列xp1(n)的共軛對稱序列，即

序列xp3(n)是通過對序列xp1(n)的偶數(shù)項進行取反得到的，即

序列xp4(n)是通過對序列xp2(n)的偶數(shù)項進行取反得到的，即

在文獻[13]中，序列x'p3(n)是通過對序列xp2(n)的共軛序列的偶數(shù)項進行取反得到的，即

文獻[13]中設計的前導序列結(jié)構(gòu)形如x'0(n)=[xp1(n)xp2(n)x'p3(n)xp4(n)]，在進行定時同步時利用了對頻偏敏感的時延自相關運算，從而降低了頻偏存在時的定時同步性能。因此，本文從避免使用時延自相關運算角度出發(fā)，設計了新型前導序列x0(n)。在x0(n)中，xp1(n)和xp2(n)形成共軛對稱，xp3(n)和xp4(n)形成共軛反對稱，從而在定時同步階段可以對2 個組合進行對稱自相關運算，這不僅可以簡化在接收端構(gòu)造的定時度量函數(shù)，而且使定時度量函數(shù)在正確的符號起始點存在一個尖銳的峰值，在有頻偏時，可以消除頻偏對定時同步的影響。

3.2 簡化定時度量函數(shù)與定時同步

在接收端，設接收窗口長度為N，在窗口長度內(nèi)根據(jù)提出的前導序列結(jié)構(gòu)，設置定時度量函數(shù)為

其中，P(d)為未經(jīng)過歸一化處理的相關函數(shù)。忽略噪聲和多徑的影響，由式(2)可得P(d)的表達式為

注意到，式(9)中將歸一化頻偏ε轉(zhuǎn)換為固定的相偏因子，取模值后可以消除頻偏對定時同步的影響。

R(d)為接收到的N個樣本的能量函數(shù)，表達式為

由式(8)、式(9)及式(12)可知，所提算法特殊的訓練序列結(jié)構(gòu)保證了定時度量函數(shù)M(d)只有在正確的起始點才有峰值，而在其他點幾乎為零，并且消除了頻偏對定時度量的影響，最終得到時間偏移的估計值為

在不加噪聲、不加頻偏的理想條件下，設正確的幀頭起始位置為1 001，基于PN 序列、CAZAC 序列的各同步算法的理想定時度量函數(shù)曲線如圖2 所示。

圖2 各同步算法的理想定時度量函數(shù)曲線

由圖2(a)可以看出，SC 算法由于循環(huán)前綴的存在，具有平頂效應；Minn 算法、Yang 算法雖然沒有平頂現(xiàn)象，卻有較大的旁瓣存在；Park 算法峰值尖銳，但仍有較小的旁瓣存在。由圖2(b)可以看出，所提算法、Jian 算法比Fang 算法、Shao 算法的峰值更尖銳，旁瓣更低。

因為各同步算法區(qū)別在于式(8)中P(d)及R(d)表達式不同，所以計算復雜度主要考慮P(d)及R(d)中的乘法及加法次數(shù)。各同步算法在定時同步階段的計算量統(tǒng)計如表1 所示。

表1 各同步算法在定時同步階段的計算量統(tǒng)計

N=256 時各同步算法在定時同步階段的計算復雜度如圖3 所示。

圖3 N=256 時各同步算法在定時同步階段的計算復雜度

從表1 和圖3 可以看出，在定時同步階段，Yang算法、Fang 算法和Shao 算法的計算復雜度高，而所提算法總的復數(shù)乘法次數(shù)為N+2 次，總的加法次數(shù)為N?4 次，相比于其他算法，計算復雜度有所下降。

3.3 聯(lián)合循環(huán)前綴的加權(quán)頻率同步

通常來說，對于OFDM 系統(tǒng)，頻偏可分為整數(shù)倍頻偏（下文簡稱為整偏）和小數(shù)倍頻偏（下文簡稱為小偏），本文采用聯(lián)合循環(huán)前綴的加權(quán)頻率同步方案來提高頻偏估計精度。

根據(jù)定時同步的結(jié)果，確定接收端訓練序列的起點位置，得到接收端的訓練序列，利用接收端訓練序列前后兩部分的對稱性，進行第一次小偏估計。

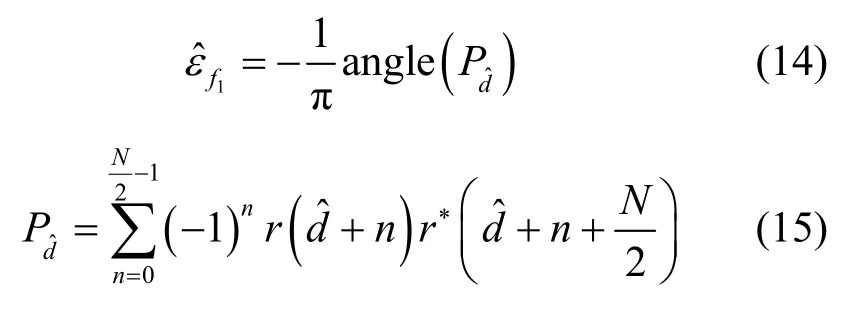
進一步地，基于循環(huán)前綴進行第二次小偏估計。

由式(14)及式(16)，得到聯(lián)合加權(quán)小偏估計值為

其中，w1和w2是與糾小偏訓練序列長度相關的權(quán)重因子，本文選擇w1=0.6，w2=0.4。

為了估計整偏，先對接收端訓練序列進行小偏補償，小偏補償后僅剩整偏。接下來，在高斯信道下分析整偏對訓練序列造成的影響，對于3.1 節(jié)中的CAZAC 序列xp1(n)，有

其中，εi為歸一化整偏，w'(n)為經(jīng)過小偏補償之后的加性白高斯噪聲。

由式(19)可得，εi造成序列xp1(n)移位，同理可得，εi造成序列xp2(n)反向移位，εi對xp1(n)、xp2(n)造成的移位影響如圖4 所示。

因此，通過與接收機本地序列進行滑動相關操作，可以完成整偏估計。

其中，r1(n)為經(jīng)過小偏補償后的接收樣本，即

由于CAZAC 序列的強自相關特性和零旁瓣特性，因此整偏估計函數(shù)會產(chǎn)生一個反映整偏的尖峰。

綜上，得到的歸一化頻偏估計值為

4 性能評估

本節(jié)仿真中，設OFDM 系統(tǒng)中子載波個數(shù)N=256，循環(huán)前綴長度NCP=32，單個信噪比的仿真次數(shù)為2 000 次，由于定時同步的結(jié)果會影響后續(xù)的頻率同步，因此采用定時檢測概率來描述其定時同步性能，定時檢測概率定義為正確檢測到幀頭的次數(shù)與蒙特卡羅仿真次數(shù)之比。

4.1 定時同步

4.1.1 抗干擾能力

在無線通信中，通常會出現(xiàn)信道噪聲，對于有用信號來說，這種噪聲便是干擾，過大的噪聲干擾會嚴重影響定時同步。因此，本節(jié)在高斯信道、無頻偏的條件下進行仿真，各同步算法的定時檢測概率如圖5 所示。

圖4 εi 對xp1(n)、xp2(n)造成的移位影響

圖5 高斯信道、無頻偏時各同步算法的定時檢測概率

從圖5 可以看出，所提算法在低信噪比條件下定時檢測性能良好，說明所提算法抗干擾能力強。

4.1.2 抗頻偏能力

多普勒頻移或振蕩器的不穩(wěn)定性會引入頻偏，對定時同步會產(chǎn)生一定的影響。所以，本節(jié)在高斯信道、加入歸一化頻偏ε=5.65 的條件下進行仿真，各同步算法的定時檢測概率如圖6 所示。

圖6 高斯信道、加入歸一化頻偏時各同步算法的定時檢測概率

從圖6 可以看出，在有頻偏時，Jian 算法定時檢測概率明顯下降。所提算法較Jian 算法而言，能消除因頻偏帶來的定時估計偏差的影響，仍具有良好的檢測性能，說明所提算法對頻偏不敏感。

4.1.3 抗多徑能力

本節(jié)在多徑衰落環(huán)境下，對各同步算法的定時性能進行了測試。多徑信道采用國際電信聯(lián)盟標準的經(jīng)典室內(nèi)ITU-R（international telecommunication union-radiocommunicaon）3G itur3GIBx[16]信道模型，在加入歸一化頻偏ε=5.65 的條件下進行仿真，各同步算法的定時檢測概率如圖7 所示。

圖7 多徑衰落信道加入歸一化頻偏時各同步算法的定時檢測概率

從圖7 可以看出，在多徑衰落信道、加頻偏的條件下，各同步算法的定時檢測概率較高斯信道均有不同程度下降，相較而言，所提算法仍具有良好的檢測性能，說明所提算法抗多徑能力強。

4.1.4 綜合性能評估

各同步算法在定時同步階段的綜合性能評估如表2 所示。

從表2 中可以看出，所提算法的綜合性能最好。

4.2 頻率同步

在不同信道，不同信噪比條件下，設加入歸一化頻偏ε=5.65，SC 算法、Fang 算法、Shao 算法以及所提算法的頻偏估計均方誤差（MSE,meansquare error）性能如圖8 所示。

表2 各同步算法在定時同步階段的綜合性能評估

圖8 各同步算法頻偏估計MSE 性能

從圖8 可以看出，在高斯信道和多徑衰落信道下，所提算法頻偏估計MSE 性能優(yōu)于SC 算法、Fang算法及Shao 算法。

另外，SC 算法進行頻偏估計時需要利用2 個前導序列，而且在接收端需要進行快速傅里葉變換（FFT,fast Fourier transform）處理，所提算法、Fang 算法以及Shao 算法僅需要利用一個前導序列，接收端也不需要進行FFT 處理，相比SC 算法，節(jié)約了一半的前導資源，也減小了計算復雜度。Shao 算法在進行頻偏估計時有一定的性能損失，F(xiàn)ang 算法在進行頻偏估計時仍需要額外利用本地的加權(quán)序列，計算復雜度較所提算法高。綜上所述，所提算法的頻偏估計性能較好。

5 結(jié)束語

本文提出了一種基于CAZAC 序列的低復雜度抗頻偏同步算法。仿真結(jié)果表明，在高斯信道和多徑衰落信道環(huán)境下，所提算法在進行定時同步時，抗干擾、抗頻偏、抗多徑性能良好且計算復雜度低；在進行頻率同步時，頻偏估計MSE 性能優(yōu)于其他算法。需要說明的是，所提算法針對突發(fā)通信系統(tǒng)，需要突發(fā)幀結(jié)構(gòu)中具備已知同步序列，相對不需要數(shù)據(jù)輔助的盲估計算法，雖然性能優(yōu)勢明顯，但在一定程度上會犧牲系統(tǒng)傳輸效率。