改進差分進化算法在四桿機構中的應用

湯雙清，華恒，丁小慧

改進差分進化算法在四桿機構中的應用

湯雙清，華恒，丁小慧

（三峽大學 機械與動力學院，湖北 宜昌 443002）

針對平面四桿機構應用廣泛，但軌跡偏差較大的問題，利用基于天牛須搜索的差分進化算法（BASDE）的新方法，旨在探討改進差分進化算法，并減小四桿機構軌跡偏差，尋找更加合理的結構尺寸。通過MATLAB軟件仿真的結果，可以看出四種優化方法中BASDE優化速度更快，收斂精度更高優化結果更好。將優化結果通過三維建模，在ADAMS軟件中進行動力學仿真，結果表明優化后的機構執行點的角加速度和線加速度均有所減小，顯示出機構軌跡偏差有所減小、運行更加平穩，運動軌跡更接近目標軌跡。

四桿機構；軌跡偏差；天牛須搜索；差分進化

四桿機構是生活中最常見的平面機構之一，上至航天器材飛機起落架[1]，下至居家縫紉機[2]，尤其是在工農業中被廣泛使用，例如巖石破碎機、糖果包裝機推糖機構[3]、秋后立稈的殘膜回收機[4]等。四桿機構是許多復雜機構的基礎，而平面四桿機構的軌跡綜合是機構設計的基本問題之一，其主要目的是找到一個平面四桿機構，使得連桿機構上的點能沿某一預先給定的軌跡行走[5]。高精度的四桿機構運動軌跡是改善設計質量，提高工作效率的基礎。因此，對四桿機構的運動軌跡進行優化設計是很有必要的。

隨著科學技術的快速發展以及計算機性能的提高，傳統的優化方法由于耗時長、精度低等缺點已慢慢退出舞臺。而智能優化算法可應對復雜問題、優化精度高等優點逐漸得到越來越多專家和學者的青睞。黃裘俊等[6]提出了二次拉格朗日插值粒子群算法優化機械手取件，優化后的機械手運動軌跡精度更高。楊帆等[7]采用改進粒子群優化算法對四桿機構幾何參數變量進行優化，提高機構的運動精度。王良詣等[8]結合遺傳算法和擬牛頓混合算法，提出一種新方法。雖然這些算法都能較好求解軌跡綜合問題，但是，由于求解問題的復雜性，對于求解方法的精度和可靠性，仍有可以改進的空間[9]。

差分進化算法是一種基于群體的自適應全局優化現代智能理論算法，具有結構簡單、易于使用、性能優越、自適應強等優點，被廣泛使用[10]。盡管差分進化算法在很多領域取得了成功應用，但其仍然存在一些不足。天牛須搜索算法雖然收斂快，但是易出現早熟現象。本文提出將差分進化算法與天牛須搜索算法混合，得到一種快速尋優、避免陷入局部最優的新方法，通過對平面四桿機構的運動軌跡進行優化設計發現該方法的搜索速度和精度得到了提高。

1 差分進化算法原理

差分進化算法（differential evolution，DE）的基本思想是：通過把隨機產生的初始種群中的兩個個體之間進行加權差向量，然后與第三個個體相加產生新的個體。最后，新個體與當代個體進行‘適者生存’策略，通過不斷地進化，優勝劣汰尋找全局最優。差分進化算法只有變異、交叉、選擇這三個核心操作過程。

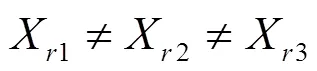
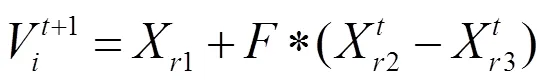
交叉操作如下：

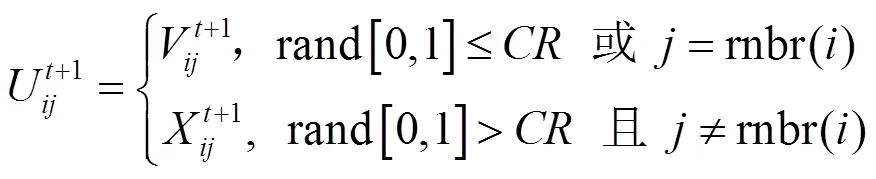
通過變異操作和交叉操作后對產生的子群體采用一對一選擇操作，較優者保留：

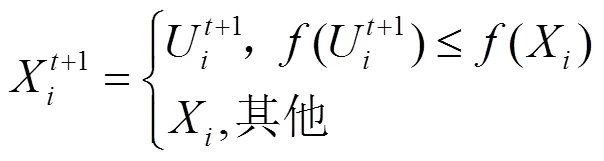
式中：(X)為個體X的適應值。

2 天牛須搜索算法

天牛須搜索算法（Beetle Antennae Search Algorithm，BAS），也叫甲殼蟲須搜索算法，是2017年提出的一種高效的生物啟發式智能優化算法[11]。天牛須搜索算法通過模擬自然界中天牛覓食行為，天牛在沒有任何提示的情況下，有快速、準確找到食物的能力。

天牛須搜索的主要原理是依據食物的氣味濃度，由于天牛不知道食物的具體位置，便依據左右兩只長觸角接收到食物氣味濃度的大小，若右邊觸角收到的氣味強度大于左邊，天牛便會往右飛行，如若不然便往左飛行，依次循環直到找到食物。

BAS流程描述如下：

（1）隨機生成一只可以向任意方向前進的天牛，用生成隨機向量來表示并歸一化：

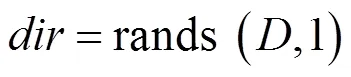
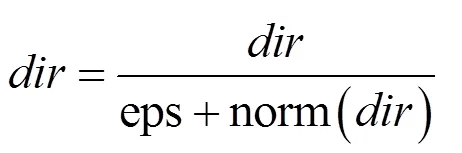
（2）左右兩須坐標為：

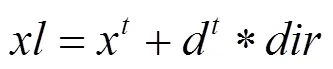
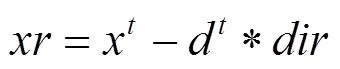
式中：x為時刻天牛的位置；d為時刻兩須之間的距離。

（3）由氣味強度決定天牛前進方向為：

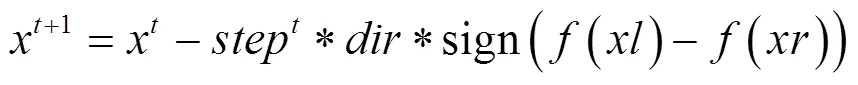
（4）兩須間的距離和步長更新：

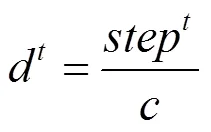
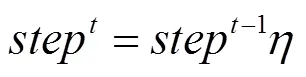
式中：為常數，取5；為步長的更新衰減系數，取0.95。

3 基于天牛須搜索的差分進化算法

天牛須搜索算法是個體的尋優，沒有群體間的交流。差分進化是基于群體智能理論的優化算法，是通過群內個體間的合作與競爭而產生尋優搜索算法。因此，本文將差分進化算法與天牛須搜索算法混合在一起，提出一種新的優化算法天牛須搜索的差分進化算法（BASDE）。該混合算法是在DE算法的基礎上，對變異向量進行改進，然后融合BAS算法對位置更新，直到尋到全局最優解。天牛須搜索算法的引入使得差分進化算法能夠避免算法陷入局部最優，增強局部搜索能力。

改進算法后天牛群的位置為：

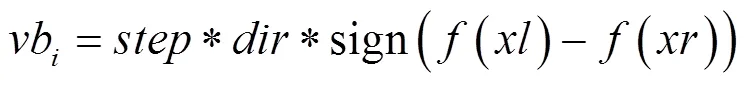
融入天牛須搜索后的差分進化算法的流程如下：

step1 初始化算法參數，設置DE種群為NP，設置變異算子0、最大進化代數G、交叉算子天牛須距離0等。

step2 隨機產生初始種群，進化代數＝1。

step3 計算種群的每個個體的適應度函數值。

step4 計算天牛下一步前進方向。

step5 更新天牛群位置，更新步長、天牛須距離、變異算子等參數，根據式（1）和式（2）進行變異、交叉操作。

step6 根據式（3）進行選擇，判斷個體是否可以成為新個體。

step7 令＝＋1，轉到step3。

step8 滿足終止條件，結束。

4 實例分析

為驗證本文所提混合算法的可行性，選取平面連桿機構的優化設計為例。平面四桿機構簡圖模型，如圖1所示，已知點的位置如表1所示。

（1）曲柄連桿的設計變量

曲柄連桿的設計變量可構成矢量為：

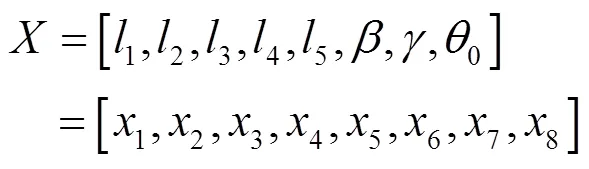
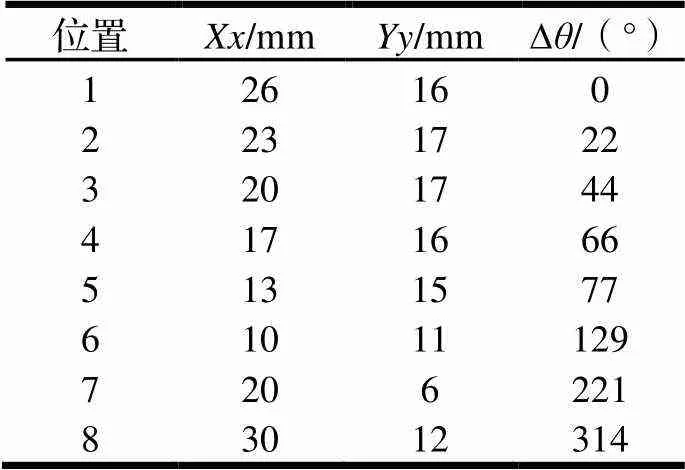
表1 點M的已知位置坐標

對點建立數學模型，由幾何關系得其運動方程為：

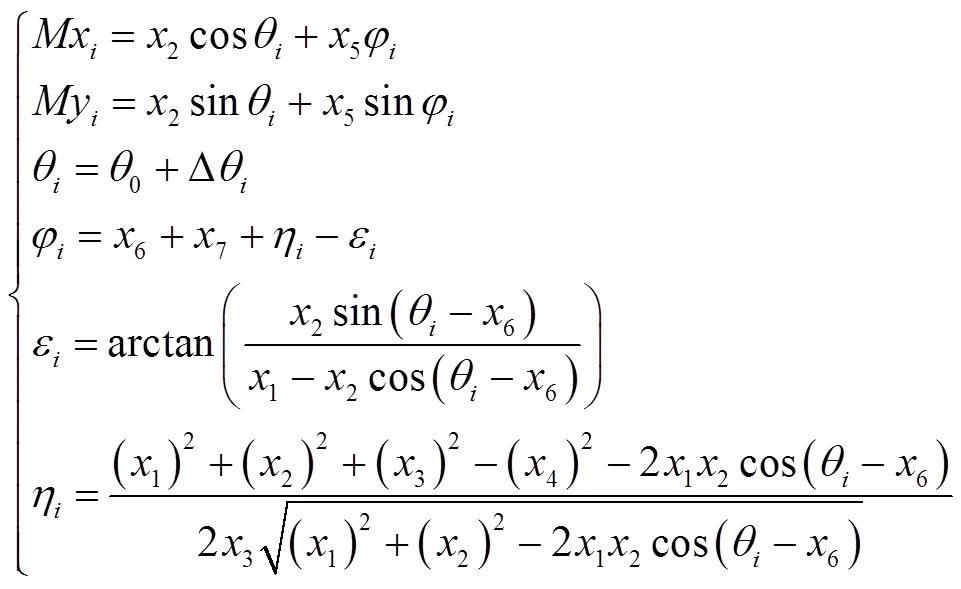
式中：Δ為曲柄轉角的0在第個位置的角增量。

（2）優化目標

選為點坐標的偏差均方根值為：

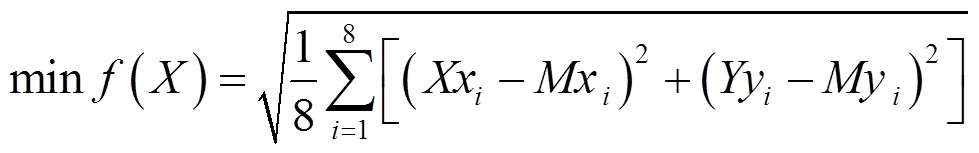
（3）約束條件

曲柄連桿的設計變量范圍為：

根據曲柄存在的條件以及最小傳動角的要求建立約束方程。

（4）目標函數

對優化目標和不等式約束采用增廣乘子法，使其轉變為無約束目標函數：

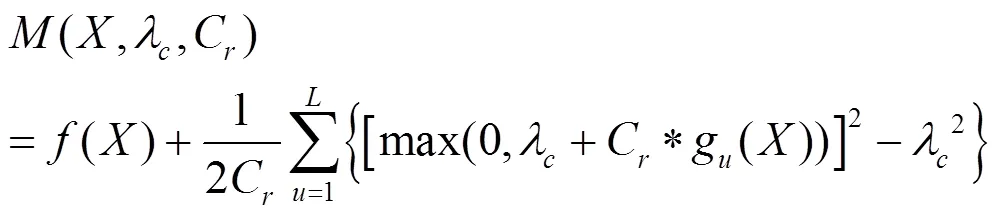
式中：Cr為罰因子；L為約束條件個數；λc為乘子；gu(X)為不等式約束方程。

表2 四桿機構的實驗結果

由表2可以看出模擬退火算法迭代次數最多，且優化結果最差，而標準差分進化算法相對文獻[12]所采用的改進遺傳算法偏差。本文所提出的BASDE算法由圖2可以看出相比較其他算法明顯具有收斂精度高、速度快、優化效果更好等優點。

將優化的結果在三維軟件中建模，導入ADAMS中仿真。優化前點的線加速度最大值在SA和DE分別為7289.9 mm/s2、7090.3 mm/s2，經BASDE優化后為6929 mm/s2。優化前點的角加速度最大值在SA和DE分別為9389.5o/s2、8679.4o/s2，經BASDE優化后為8635o/s2。由圖3和圖4可看出，優化后的執行點的角加速度和線加速度均有所減小，機構運動更平穩。

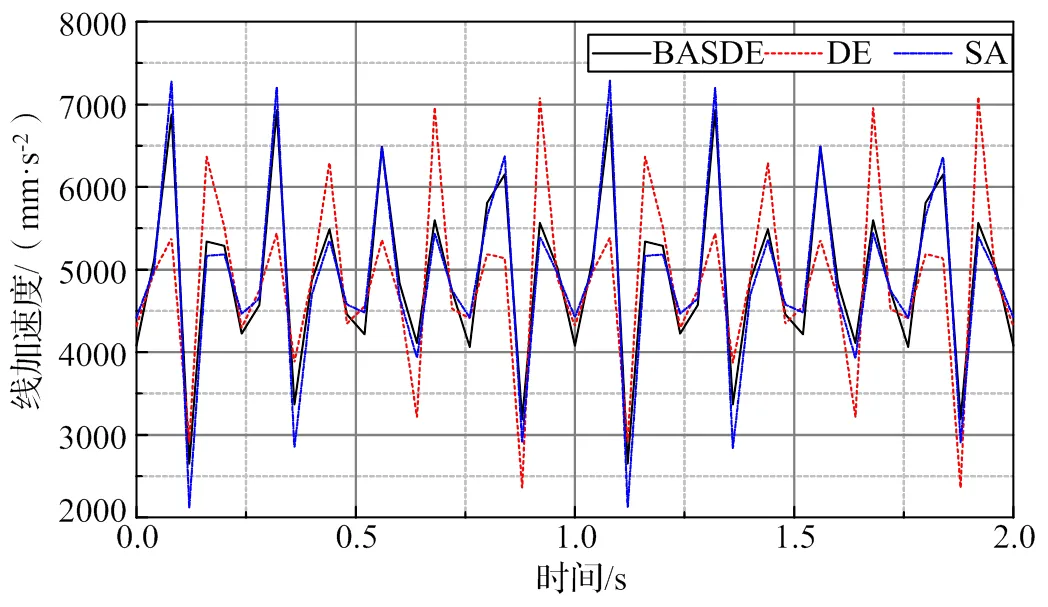
圖3 M點的線加速度

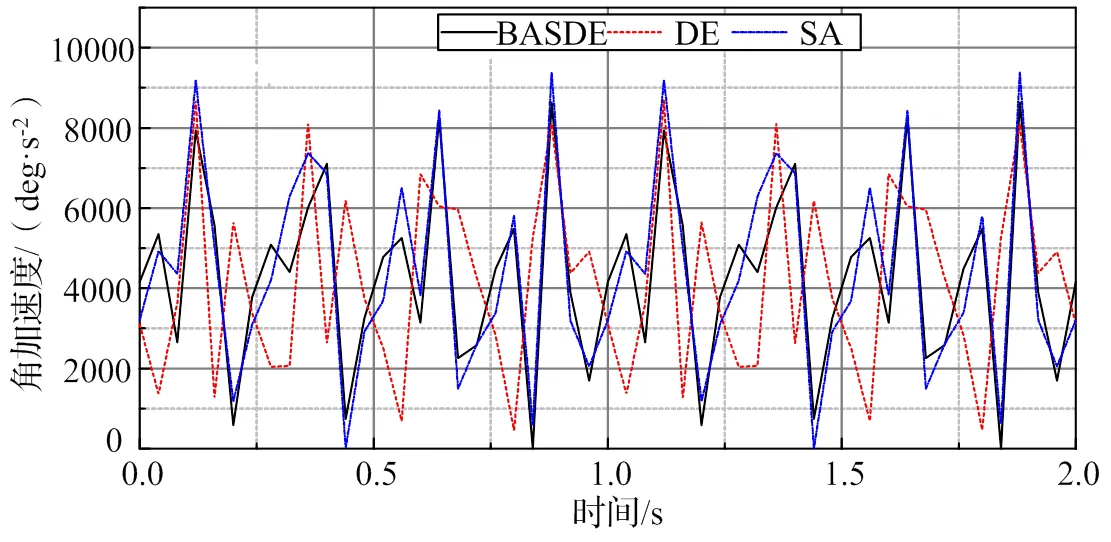
圖4 M點的角加速度

5 結論

針對平面連桿機構軌跡生成問題，提出一種基于天牛須搜索算法的差分進化算法，采用增廣乘子法構造無約束目標函數，對平面連桿機構軌跡優化，在滿足約束條件下，尋優效果更好。仿真結果表明本算法具有搜索能力強、快速尋優、求解精度高，且克服了差分進化算法陷入局部最優的缺點，可以使軌跡更好的接近目標曲線，使軌跡偏差更小。

[1]張文彬，沈精虎，張敏. 基于Creo的某機型起落架的自頂向下設計[J]. 機械，2017，44（5）：14-16，65.

[2]周長江，劉亞輝，吳長德. 基于響應面法的平縫機刺布挑線機構動平衡優化[J]. 湖南大學學報（自然科學版），2013，40（8）：64-68.

[3]郎詩慧，辛洪兵. 糖果包裝機推糖機構的運動精度分析[J]. 包裝工程，2017（5）：59-67.

[4]孫興凍，陳玉龍，羅昕，等. 針對秋后立稈模式的殘膜回收機的設計[J]. 農機化研究，2015，37（9）：73-76.

[5]袁佩瑤，林松，王瀚超. 基于幾何法的空間連桿機構三位置函數綜合[J]. 機械，2019，46（11）：16-21.

[6]黃裘俊，張凱，宋錦春，等. 基于改進粒子群算法的取件機械手軌跡綜合優化設計[J]. 東北大學學報（自然科學版），2018，39（11）：119-124.

[7]楊帆，周麗紅. 基于改進粒子群優化的四桿機構運動軌跡誤差研究[J]. 組合機床與自動化加工技術，2018（2）：5-8.

[8]王良詣，姜禮杰，王勇. 基于遺傳擬牛頓混合算法的四桿機構優化[J]. 合肥工業大學學報：自然科學版，2018，41（2）：150-153.

[9]Lin W Y，Hsiao K M. A new differential evolution algorithm with a combined mutation strategy for optimum synthesis of path-generating four-bar mechanisms[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science，2017，231（14）：2690-2705.

[10]蔡之華，龔文引. 差分演化算法及其應用[M]. 武漢：中國地質大學出版社， 2010：15-17.

[11]Jiang X, Li S. BAS: Beetle Antennae Search Algorithm for Optimization Problems [J]. International Journal of Robotics and Control, 2017, 1(1).

[12]葉彬，羅金良. 改進FGA算法及其在四桿機構優化設計中的應用[J]. 機械傳動，2017，41（7）：176-179.

Application of Improved Differential Evolution Algorithms in Four-bar Linkages

TANG Shuangqing，HUA Heng，DING Xiaohui

( College of Mechanical & Power Engineering, China Three Gorges University,Yichang 443002,China )

Aiming at the problem that the planar four-bar linkage is widely used, but the track deviation is large, a new method of Differential Evolution algorithm based on Beetle Antennae Search algorithm (BASDE) is employed to reduce the track deviation of the four-bar mechanism and find a more reasonable structure size. The results of the MATLAB software simulation indicates that among the four optimization methods, BASDE has faster optimization speed, higher convergence accuracy and better optimization result. The three-dimensional model of the optimization result is built, and the dynamics simulation is performed in ADAMS software, which shows that the angular acceleration and linear acceleration of the optimized mechanism execution point are reduced, the trajectory deviation of the mechanism is reduced, the operation is more stable, and the motion trajectory is closer to the target trajectory.

four-bar linkage；trajectory deviation；beetle antennae search；differential evolution

TH112

A

10.3969/j.issn.1006-0316.2021.01.001

1006－0316 (2021) 01－0001－05

2020－09－22

國家自然科學基金（51175297）

湯雙清（1962－），男，湖北孝感人，博士、教授，碩士生導師，主要研究方向為機械設計及理論，E-mail：tang_sq@ctgu.edu.cn。