提高衛(wèi)星導航精度的卡爾曼濾波算法應用研究
岳崇倫,曾 苑,郭云開,2
(1.廣州城建職業(yè)學院,廣東 廣州 510900;2.長沙理工大學 測繪遙感應用技術研究所,湖南 長沙 410076)
汽車、火車、輪船等交通運輸工具在人們的日常生活中扮演著不可或缺的角色,它們的速度是體現(xiàn)它們性能的重要指標之一,如何測量它們的速度現(xiàn)在已經(jīng)有很多方法,而如何提高測速精度是現(xiàn)在研究的重點。對于海上行駛的交通運輸工具來說,精確測量它們的速度更加難,大海上沒有參照物,也不可能架設雷達等設備,因成本太高。
2020 年 6 月全面建成的北斗三號系統(tǒng)將為全球用戶提供授時、定位導航、全球短報文通信和國際搜救服務,同時可為中國及周邊地區(qū)用戶提供星基增強、地基增強、精密單點定位和區(qū)域短報文通信等服務。北斗衛(wèi)星導航系統(tǒng)(BeiDou Navigation Satellite System,BDS)作為著眼于國家安全和經(jīng)濟社會發(fā)展需要的國家重要時空基礎設施,是中國戰(zhàn)略性新興產(chǎn)業(yè)發(fā)展的重要領域。BDS 已成為聯(lián)合國衛(wèi)星導航委員會認定的全球四大導航系統(tǒng)之一。相比于 GPS 的信號可靠性不能充分保障、易受“干擾”等弊端,BDS 具有抗遮擋能力強、服務精度更高、服務能力更強等特點。隨著我國衛(wèi)星事業(yè)的發(fā)展,其應用功能和性能有很大提高空間[1]。交通運輸部表示,2020年將在交通運輸系統(tǒng)的道路客運車輛、城市里的配送車輛、公交車、長江干線的船舶以及飛機、火車全面推廣使用北斗衛(wèi)星的應用。北斗三號系統(tǒng)的建成推進了衛(wèi)星導航定位在汽車、火車、輪船等交通運輸工具中的廣泛應用。
海上航行用的定位方法幾乎都是衛(wèi)星導航,衛(wèi)星導航不但可以進行定位,還可以進行測速。衛(wèi)星導航系統(tǒng)在測速方面的應用已經(jīng)十分廣泛,尤其是在海上航行時,衛(wèi)星導航是測量輪船速度最好的方法,因此衛(wèi)星導航測速廣泛應用于航海。目前應用于輪船動態(tài)測速的方法[2]主要以基于GPS動態(tài)測速方法為主,包含GPS多普勒頻移測速和GPS差分測速,但都存在一定不足,這兩種方法測速準確性有待提高。然而,衛(wèi)星導航測速是存在誤差的,這些誤差一般都是偶然誤差,而且當物體低速行駛時,誤差更明顯。衛(wèi)星導航接收機顯示的速度一般都包含噪聲,這些噪聲是隨機的,屬于高斯白噪聲,如何消除或減少這些噪聲是當前研究的重點。卡爾曼濾波[3]對于消除高斯白噪聲是一種很好的方法,對于提高衛(wèi)星導航測速精度有很好的效果。為此本文提出了利用卡爾曼濾波算法消除或減少噪音以提高衛(wèi)星導航測速精度,并進行實驗驗證。
1 卡爾曼濾波
卡爾曼濾波是基于狀態(tài)空間方法的一套遞推濾波算法,在狀態(tài)空間方法中,引入了狀態(tài)變量的概念。卡爾曼濾波模型包括狀態(tài)向量和觀測向量,狀態(tài)向量每時每刻都在變化,這種變化可以用一個方程表示,而觀測向量也可以用一個方程表示,這兩個方程就組成了卡爾曼濾波模型。卡爾曼濾波首先通過狀態(tài)轉移方程預測下一個狀態(tài),再根據(jù)觀測變量來得到系統(tǒng)的最優(yōu)估計[4-7]。
用一幅簡單的流程圖來表示卡爾曼濾波工作的基本流程,見圖1。

圖1 卡爾曼濾波工作的基本流程圖
2 卡爾曼濾波在提高衛(wèi)星導航精度的應用
衛(wèi)星導航接收機可以實時接收衛(wèi)星信號,計算出船舶的速度。但由于導航衛(wèi)星播發(fā)的信號存在噪聲干擾,加上海上情況復雜多變,衛(wèi)星導航接收機計算的速度含有噪聲數(shù)據(jù),為了提高衛(wèi)星導航測速精度,需對數(shù)據(jù)進行濾波處理,卡爾曼濾波是最好的方法[8-10]。
2.1 卡爾曼濾波模型的建立
假設船舶在n-1時刻的速度為v(n-1),n時刻船舶速度為v(n)。n-1到n時刻的時間間隔為T,T=1 s,由于時間間隔T很小,因此可假設船舶在n-1到n時刻的加速度恒定為a(n-1),則船舶在n時刻的速度表達式為:
v(n)=v(n-1)+a(n-1).
(1)
船舶在n時刻的加速度表達式為:
a(n)=u(n)+w(n).
(2)

下面定義狀態(tài)矩陣:

(3)
式中:v(n)表示船舶在n時刻的速度,a(n)表示船舶在n時刻的加速度,將式(1)和式(2)代入式(3)可得卡爾曼濾波狀態(tài)方程:


F·X(n-1)+U(n)+W(n) .
(4)

設卡爾曼濾波的測量方程為:
Y(n)=H·X(n)+R(n).
(5)

可得卡爾曼濾波模型為:
X(n)=F·X(n-1)+U(n)+W(n),
(6)
Y(n)=H·X(n)+R(n).
(7)
到此卡爾曼濾波模型已經(jīng)建立,根據(jù)模型得出卡爾曼濾波器5個方程:
狀態(tài)預測方程:
X-(n)=F·X(n-1)+U(n);
(8)
協(xié)方差預測方程:
P-(n)=F·P(n-1)·FT+Q;
(9)
濾波增益方程:
K=P-(n)·HT(H·P-(n)·HT+R)-1;
(10)
狀態(tài)更新方程:
X(n)=X-(n)+K(Y(n)-HX-(n));
(11)
協(xié)方差更新方程:
P(n)=(1-K·H)P-(n).
(12)
2.2 實驗數(shù)據(jù)和卡爾曼濾波參數(shù)
在卡爾曼濾波模型中,只需已知測量數(shù)據(jù)Y(n),船舶在n時刻的系統(tǒng)加速度u(n),初始狀態(tài)數(shù)據(jù)X(0)和初始協(xié)方差矩陣P(0),系統(tǒng)噪聲協(xié)方差矩陣Q,觀測噪聲R,通過迭代求出最優(yōu)解。
一艘輪船在海上行駛,船上安裝衛(wèi)星導航接收機,衛(wèi)星導航接收機實時顯示每一秒輪船的速度(單位為海里),記錄下輪船在一段時間內(nèi)每秒的速度。記錄的數(shù)據(jù)見表1輪船速度測量值表。

表1 輪船速度測量值表

確定觀測噪聲R,雖然衛(wèi)星導航接收機計算出來的速度有誤差,但誤差不會太大,通過大量數(shù)據(jù)分析表明,觀測數(shù)據(jù)誤差不會超過1,因此可得觀測噪聲R=1。
接下來確定初始值,初始狀態(tài)數(shù)據(jù)的第一個量用第一個速度值表示,第二個量為0,因此可以確定初始狀態(tài)數(shù)據(jù)
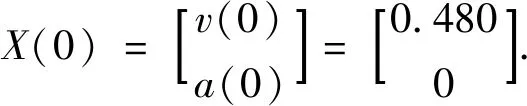
2.3 Matlab仿真程序
本文的Matlab程序是在Matlab 7.0上編寫和運行的。Matlab代碼:
X=[0.480; 0]; %狀態(tài)初值
P=[1 0; 0 1]; %狀態(tài)協(xié)方差矩陣
F=[1 1; 0 0]; %狀態(tài)轉移矩陣
Q=[0,0;0,1]; %狀態(tài)轉移協(xié)方差矩陣
H=[1 0]; %觀測矩陣
R=1; %觀測噪聲方差
Y=[ 0.480,0.470,0.460,……];%觀測數(shù)據(jù),完整數(shù)據(jù)見表1
Z= zeros(1,120);
U=[0;0];%加速度初值
for i=1:120
if i>=2
U= [0;Y(i)-X(1)];
end
X_ = F*X+U;
P_ = F*P*F'+Q;
K = P_*H'/ (H*P_*H'+R);
X = X_+K*( Y(i) -H*X_);
P = ( eye(2) -K*H)*P_;
Z(i)=X(1);
End
figure;
hold on;
T=1:120;
plot(T,Y);%畫出觀測值圖形
figure;
hold on;
plot(T,Z); %畫出濾波值圖形
figure;
hold on;
plot(T,Y);
plot(T,Z,‘r’); %畫出觀測值與濾波值
figure;
hold on;
plot(T,Z-Y); %畫出觀測值與濾波值之差圖形
2.4 實驗結果分析
觀測數(shù)據(jù)對應的折線圖如圖2所示,由圖可明顯的看出有幾個數(shù)據(jù)跳躍十分大,這顯然是不合理的,可以將這些數(shù)據(jù)稱之為噪聲數(shù)據(jù),卡爾曼濾波可以很好的處理這些數(shù)據(jù)。經(jīng)過卡爾曼濾波處理后得到的數(shù)據(jù)如表2所示。

表2 輪船速度濾波后數(shù)據(jù)表

續(xù)表2
輪船速度濾波后的值對應的折線圖如圖3所示,很顯然在圖2中跳躍很明顯的數(shù)據(jù)已經(jīng)趨于平緩,卡爾曼濾波有了效果。
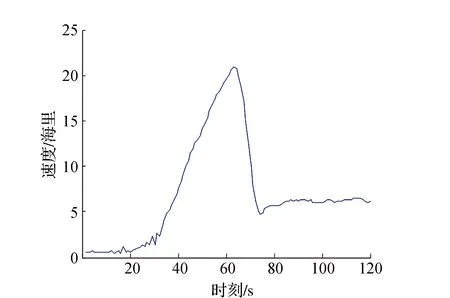
圖2 輪船速度測量值

圖3 濾波后輪船速度值

圖4 輪船速度測量值與濾波后速度值比較圖

圖5 輪船速度測量值與濾波后速度值之差
觀察表1的觀測數(shù)據(jù),在26 s、27 s、28 s、29 s、30 s、31 s、32 s、33 s、34 s這些時刻的數(shù)據(jù)為1.110海里、1.720海里、1.280海里、2.230海里、1.310海里、2.660海里、2.270海里、3.380海里、4.060海里,這些數(shù)據(jù)跳躍十分大,很明顯有些數(shù)據(jù)是噪聲數(shù)據(jù),經(jīng)過濾波后,這些數(shù)據(jù)變?yōu)?.244海里、1.484海里、1.539海里、1.888海里、1.794海里、2.108海里、2.538海里、3.120海里、4.022海里,可以看出,這些數(shù)據(jù)變得更加平滑,更加準確。
綜上,卡爾曼濾波提高對船舶衛(wèi)星導航測速精度有很大效果。
3 結束語
本文實驗測出了一艘輪船在海上一段時間內(nèi)行駛速度,受外界因素的干擾,衛(wèi)星導航測速得到的數(shù)據(jù)含有噪聲數(shù)據(jù),本研究用卡爾曼濾波對含有隨機噪聲的數(shù)據(jù)有很好的過濾效果。通過卡爾曼濾波器對測出的數(shù)據(jù)進行估計,得到相對更精確的數(shù)據(jù);通過對比濾波前、后的數(shù)據(jù),可明顯看出濾波后的數(shù)據(jù)更精確,因此卡爾曼濾波對提高衛(wèi)星導航精度效果比較理想。北斗作為我國的重要戰(zhàn)略性技術,從長遠看基于BDS的時空信息服務是智能導航的一個重要基礎組件,實現(xiàn)衛(wèi)星導航中的時空信息服務“無處不在,需則可用”是大勢所趨。隨著BDS的發(fā)展,衛(wèi)星導航行業(yè)的應用場景挖掘是一個很重要的發(fā)展方向。在統(tǒng)一規(guī)劃時空信息服務支撐框架基礎上,提高服務精度尋求恰當?shù)膽脠鼍笆荁DS切實助力導航技術發(fā)展的關鍵。

